TL;DR#
Many machine learning applications involve mapping between function spaces, often requiring discretization for computation. Neural operators excel at this, but their discretization can be problematic in infinite-dimensional spaces. This paper investigates the theoretical limits of continuously discretizing neural operators, focusing on bijective operators seen as diffeomorphisms. It highlights challenges arising from the lack of a continuous approximation between Hilbert and finite-dimensional spaces.
The paper introduces a new framework using category theory to rigorously study discretization. It proves that while continuous discretization isn’t generally feasible, a significant class of operators—strongly monotone operators—can be continuously approximated. Furthermore, the paper shows bilipschitz operators, a more practical generalization of bijective operators, can always be expressed as compositions of strongly monotone operators, enabling reliable discretization. A quantitative approximation result is provided, solidifying the framework’s practical value.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on neural operators and scientific machine learning. It addresses the critical issue of discretization in infinite-dimensional spaces, providing a rigorous framework and theoretical foundation for developing robust and reliable numerical methods. The findings are relevant to many applications involving PDEs and function spaces, offering new avenues for research on continuous approximation and discretization invariance.
Visual Insights#

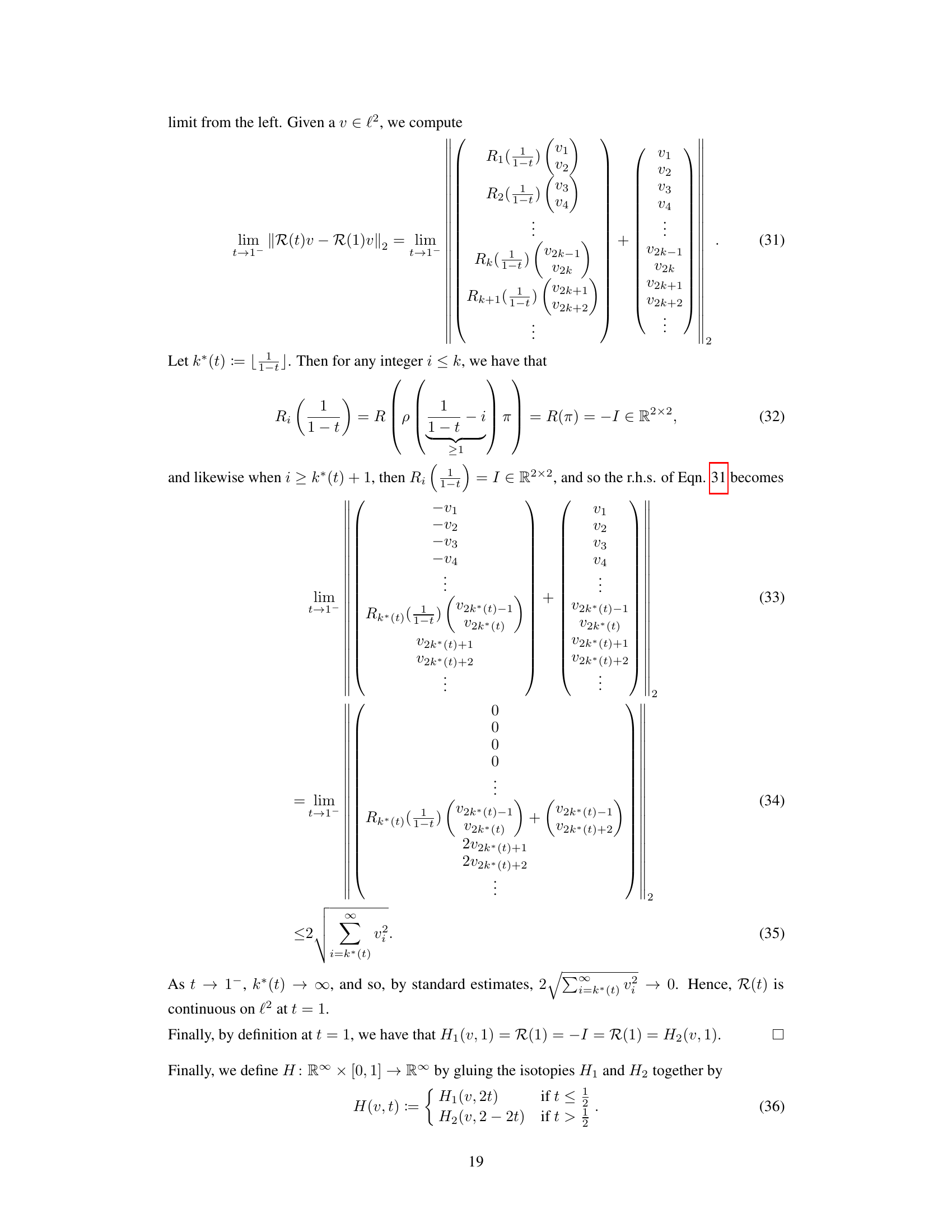
🔼 The figure illustrates the proof of Theorem 2 by showing the disconnected components of diffeomorphisms that preserve orientation (diff⁺) and reverse orientation (diff⁻) for finite-dimensional vector spaces V. As the dimension of V increases toward infinity (becoming a Hilbert space H), these components connect. This disconnection in finite dimensions, but connection in infinite dimensions, is key to the proof’s contradiction.
read the caption
Figure 1: A figure illustrating the proof ideas for Theorem 2. It represents the disconnected components of diffeomorphisms that preserve orientation, notated by diff⁺, and reverse orientation, notated, diff⁻. The horizontal axis abstractly represents the two disconnected components of diff for a finite-dimensional vector space V. The vertical axis represents the dimension of V. Observe how the two components of diff connect as dim(V) → ∞, and V becomes a Hilbert space H.
Full paper#