↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many machine learning algorithms struggle with unbounded losses, hindering accurate generalization performance analysis. Traditional PAC-Bayes bounds often rely on restrictive assumptions and/or involve a free parameter that is difficult to optimize, leading to suboptimal results. This limits their applicability and effectiveness.
This paper introduces a novel PAC-Bayes oracle bound that overcomes these limitations. By leveraging the properties of Cramér-Chernoff bounds, the new method enables exact optimization of the free parameter, thus enhancing accuracy. Furthermore, it allows for more informative assumptions, generating potentially tighter and more useful bounds. The framework is also flexible enough to encompass a range of existing regularization techniques.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with unbounded losses in machine learning. It offers novel theoretical tools and algorithmic advancements improving the accuracy and efficiency of generalization bound calculations. The provided framework is widely applicable, extending beyond existing techniques and offering new avenues for research on tighter bounds and optimal posterior distributions.
Visual Insights#
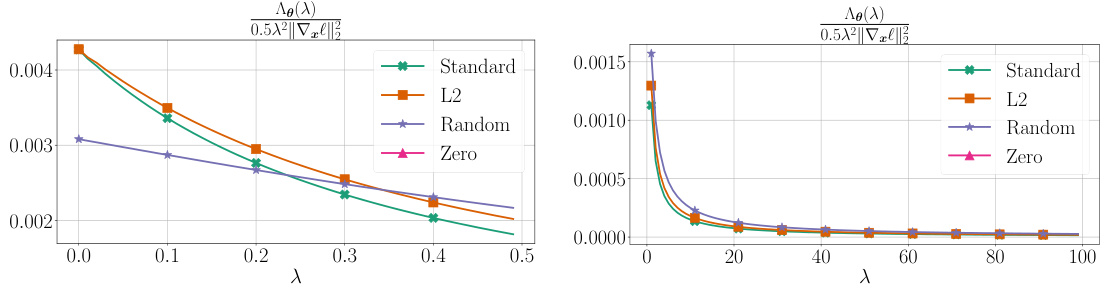
This figure shows that models with different characteristics (different regularization, random labels, zero weights) have very different cumulant generating functions (CGFs). The left panel displays several performance metrics for these models. The right panel displays the estimated CGFs, demonstrating a clear relationship between the CGFs and the other metrics, particularly the variance of the log-loss function and the L2 norm of the model parameters.

The table shows metrics for different InceptionV3 models trained on CIFAR-10 dataset. Models include a standard model, one with L2 regularization, a model with random labels, and a zero-initialized model. Metrics presented are training and testing accuracy, test log-loss, L2 norm of the model parameters, the expected squared L2 norm of input gradients, and the variance of the log-loss. The table also includes a plot of the estimated Cumulant Generating Functions (CGFs) for each model. The CGFs illustrate that models with lower variance and parameter norms have smaller CGFs.
Full paper#



















