↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Training large machine learning models often involves distributing the task across multiple devices. This poses a challenge, as communicating the gradients during training can become computationally expensive. Prior work has mainly focused on techniques that improve communication efficiency, but often these methods use a simpler, less effective gradient sampling technique (sampling with replacement). This research paper aims to improve these methods.
The paper focuses on the random reshuffling (RR) technique, a more advanced gradient sampling method (sampling without replacement). It develops new algorithms that combine RR with gradient compression to reduce the communication overhead. They introduce algorithms like Q-RR, DIANA-RR, Q-NASTYA, and DIANA-NASTYA, which incorporate different variance reduction techniques and local computation steps. The researchers provide comprehensive convergence analysis and demonstrate improved performance in various experiments.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in distributed and federated learning. It directly addresses the communication bottleneck by proposing novel methods that combine gradient compression with random reshuffling, a superior sampling technique. The findings improve upon existing algorithms and offer valuable insights into variance reduction strategies, opening up new avenues for research in communication-efficient training. The results are important for various applications such as federated learning and large-scale model training.
Visual Insights#
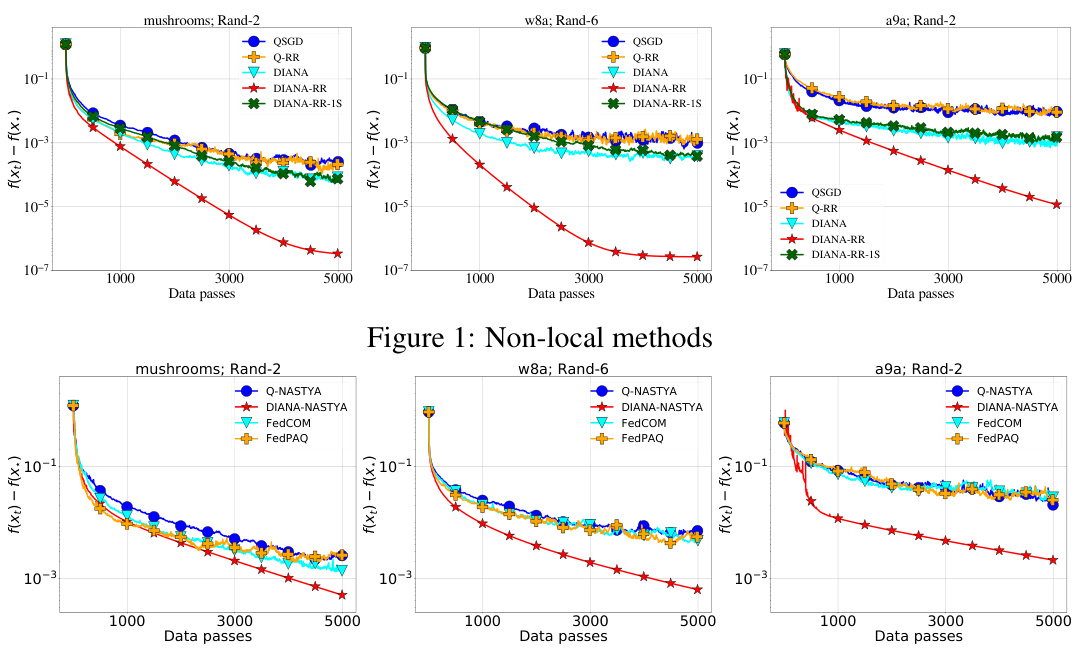
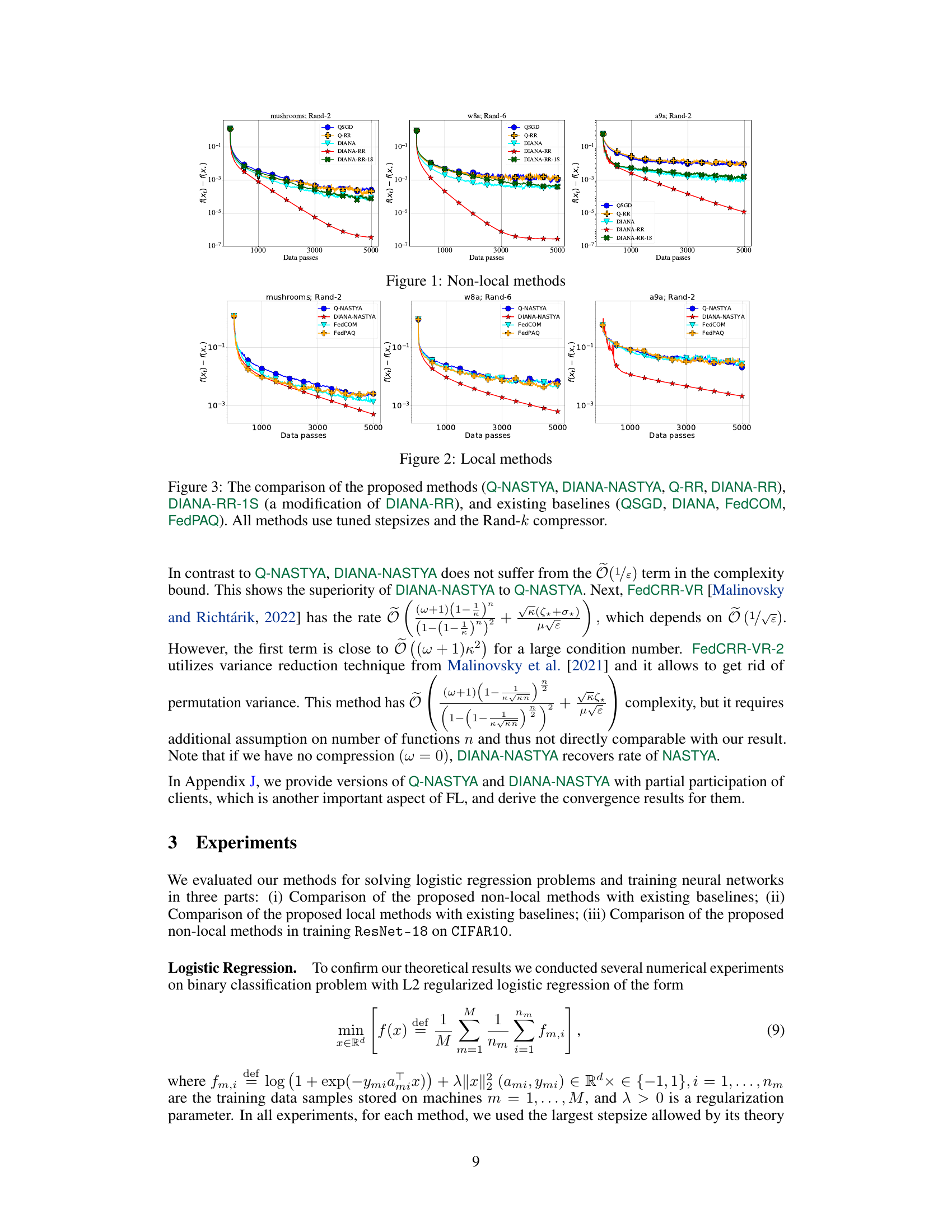
The figure compares the performance of several non-local methods for solving logistic regression problems. The methods include QSGD, Q-RR, DIANA, DIANA-RR, and DIANA-RR-1S. The results show that DIANA-RR achieves the best convergence rate among all considered methods, which aligns with the theoretical analysis in the paper.

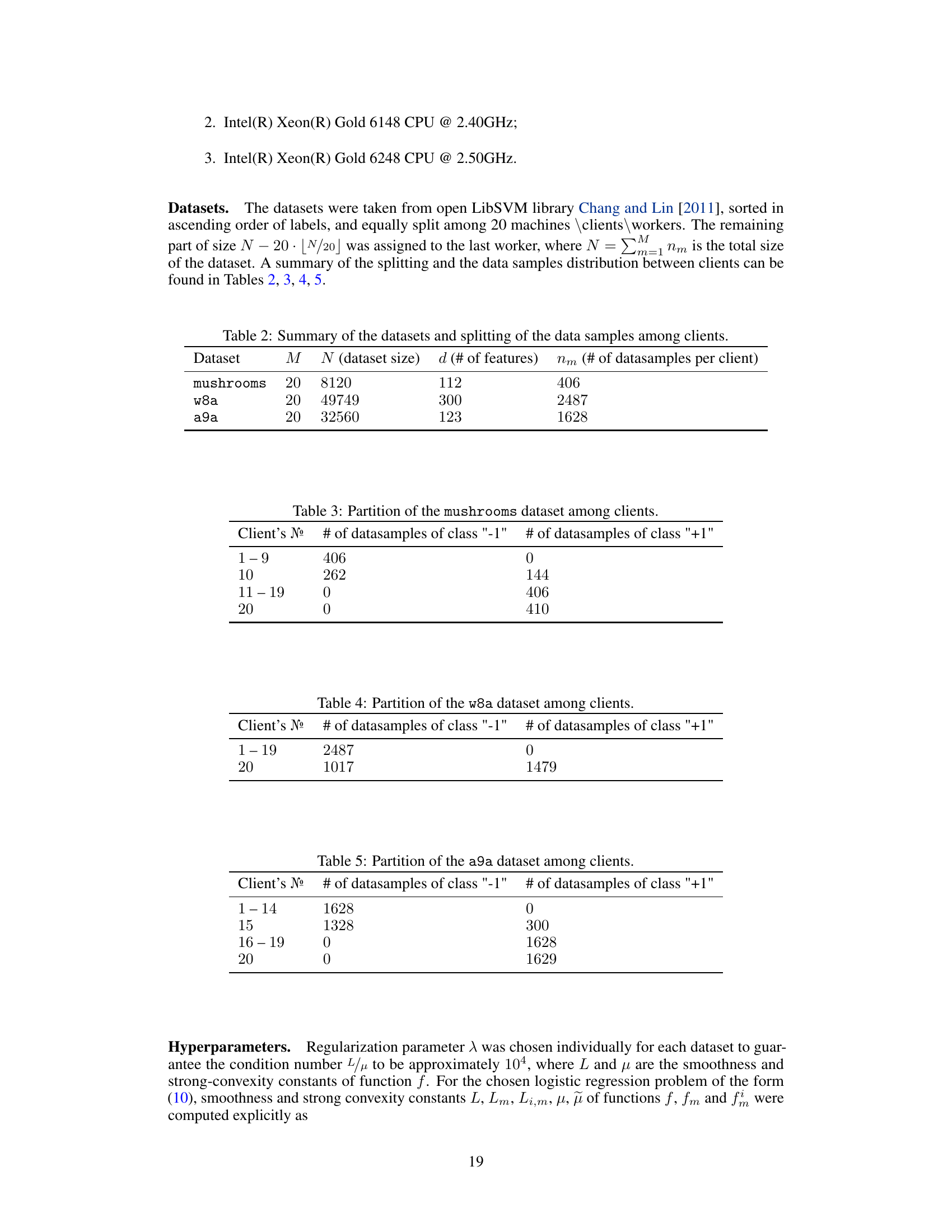
This table summarizes the communication complexities of various distributed optimization algorithms for solving finite-sum problems. It compares algorithms with and without random reshuffling (RR) and gradient compression (C), highlighting their dependence on data heterogeneity (H) and convexity assumptions (CVX). The complexity is measured by the number of communication rounds needed to achieve a certain accuracy (ε).
In-depth insights#
Compression Tradeoffs#
Compression tradeoffs in distributed machine learning involve balancing communication efficiency against model accuracy. Strong compression significantly reduces communication costs but introduces noise, potentially slowing convergence or degrading model performance. The optimal compression level depends on various factors, including network bandwidth, dataset characteristics, model architecture, and the specific optimization algorithm used. Techniques like control variates or gradient differences can help mitigate the negative impacts of compression, but they also introduce additional computational complexity. Therefore, finding the sweet spot requires careful consideration and experimentation. The choice between unbiased and biased compression also presents a tradeoff; unbiased methods introduce more variance but can theoretically converge faster. The paper explores various strategies to navigate these tradeoffs within the context of random reshuffling, demonstrating practical advantages while also considering theoretical implications.
Q-RR Algorithm#
The Q-RR algorithm, a novel distributed optimization method, integrates gradient compression and random reshuffling (RR). Its core innovation lies in applying compression to the gradients directly within the RR framework, unlike previous methods that solely focused on with-replacement sampling. This approach, while seemingly straightforward, presents challenges due to the additional variance introduced by compression. The algorithm’s analysis reveals convergence rates dependent on compression variance which is potentially a major limitation, particularly at reasonable compression levels. Despite the theoretical limitations, it serves as a foundation for subsequent improved algorithms such as DIANA-RR. DIANA-RR addresses the high variance of Q-RR by incorporating control iterates, a technique shown to effectively mitigate compression noise. Thus, Q-RR, despite its individual limitations, plays a crucial role as a stepping stone, showcasing the complexity of integrating gradient compression with RR and providing insight into the need for more sophisticated variance-reduction techniques.
DIANA-RR Variance#
The concept of ‘DIANA-RR Variance’ would revolve around analyzing the variance reduction achieved by the DIANA-RR algorithm. This algorithm is a modification to the Random Reshuffling (RR) method, which itself is an improvement over traditional stochastic gradient descent (SGD). DIANA-RR combines RR with the DIANA approach, which uses control variates to reduce the variance introduced by gradient compression. Therefore, an analysis of DIANA-RR variance would involve investigating how effectively this combined approach mitigates variance from both gradient compression and the inherent randomness of RR. This could involve both theoretical analysis, demonstrating reduced upper bounds on variance, and empirical evaluation, showcasing improved convergence rates and reduced error compared to alternative methods in various distributed and federated learning settings. A key focus would be examining how the additional shift vectors in DIANA-RR contribute to variance reduction, and how these changes impact the overall communication efficiency of the algorithm. A detailed analysis could also explore potential trade-offs. For instance, while DIANA-RR might reduce variance, it may introduce other complexities or computational costs.**
NASTYA Extensions#
The NASTYA Extensions section would delve into adapting the core NASTYA algorithm for enhanced performance in federated learning scenarios. A key focus would be on incorporating gradient compression techniques within the NASTYA framework, exploring how to minimize communication overhead without significantly sacrificing convergence speed. This could involve investigating various compression strategies, analyzing their impact on the variance of the updates, and proposing novel methods to mitigate any adverse effects. The analysis would likely include theoretical convergence bounds for the proposed modifications, comparing their performance to existing gradient compression methods. Furthermore, the extensions would likely explore the application of NASTYA to more complex or heterogeneous federated learning settings. This might include scenarios with non-independent and identically distributed data across clients or settings with significant variations in client capabilities and communication bandwidths. The robustness and scalability of the extended algorithm would be a major concern, with a careful consideration of practical limitations and trade-offs.
Federated Learning#
Federated learning (FL) is a decentralized machine learning approach that enables multiple entities, such as mobile devices or hospitals, to collaboratively train a shared model without directly sharing their local data. This is particularly important when dealing with sensitive information like patient records or financial data. Data privacy is a core principle of FL, as it allows for model training while keeping individual data points confidential on the devices. The communication efficiency is another crucial aspect of FL as it often involves resource-constrained devices. Gradient compression and random reshuffling are frequently used techniques to reduce the communication overhead. FL’s success hinges on effective strategies to manage data heterogeneity, model aggregation, and the trade-offs between communication and computation. Further research in FL focuses on improving robustness to adversarial attacks and developing efficient algorithms for diverse data distributions and network topologies. The applications of FL are rapidly expanding, with promising outcomes in areas like healthcare, finance, and IoT.
More visual insights#
More on figures
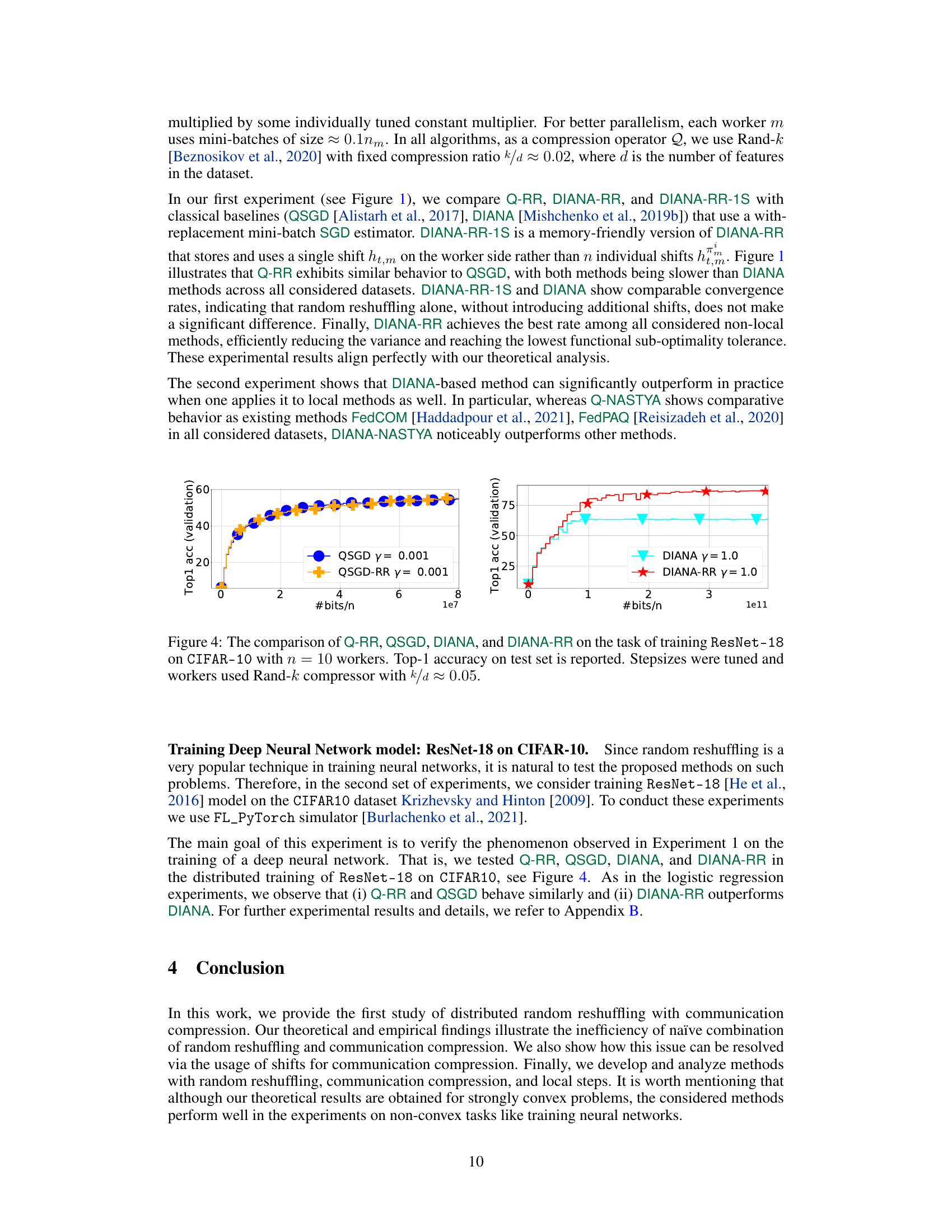
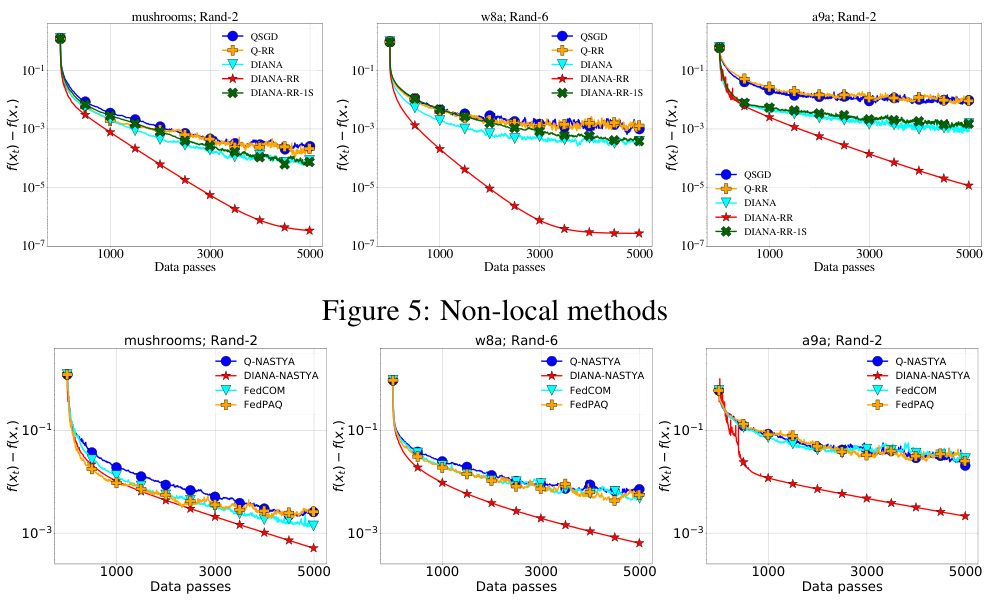
The figure compares several methods for distributed optimization using gradient compression and random reshuffling. It shows the convergence speed (f(x) - f(x*)) of the proposed algorithms Q-NASTYA, DIANA-NASTYA, Q-RR, and DIANA-RR against existing baselines QSGD, DIANA, FedCOM, and FedPAQ. The results show the performance in different settings of local steps and non-local steps (local computation vs global communication). DIANA-RR-1S is a memory-optimized version of DIANA-RR. All methods use tuned stepsizes and the Rand-k compression operator.
The figure compares the performance of several methods for non-local methods across three datasets (mushrooms, w8a, a9a) with different random reshuffling parameters. The methods include QSGD, Q-RR, DIANA, DIANA-RR, and DIANA-RR-1S. The y-axis represents the functional suboptimality, while the x-axis represents the number of data passes. The plot shows how each method converges over time on each dataset. The plot provides a visual comparison of the algorithms, showing the convergence rates of the different methods and how the different datasets affect their performance.

This figure compares the performance of DIANA-RR with two other algorithms, DIANA and EF21-SGD, on two datasets (mushrooms and a9a) using a Rand-k compressor with a compression ratio of k/d ≈ 0.02. The x-axis shows the number of data passes, while the y-axis represents the functional suboptimality (f(x) - f*). The results illustrate that DIANA-RR achieves faster convergence compared to the baselines.
This figure compares the performance of several algorithms for distributed optimization problems, including those proposed in the paper (Q-NASTYA, DIANA-NASTYA, Q-RR, DIANA-RR, DIANA-RR-1S) and existing methods (QSGD, DIANA, FedCOM, FedPAQ). The algorithms are evaluated based on their convergence rate, which is measured by the decrease in the loss function value over the training process. All algorithms use tuned stepsizes and the same compression operator (Rand-k). The results illustrate the effectiveness of the proposed algorithms, particularly DIANA-RR, which achieves the best convergence rate.
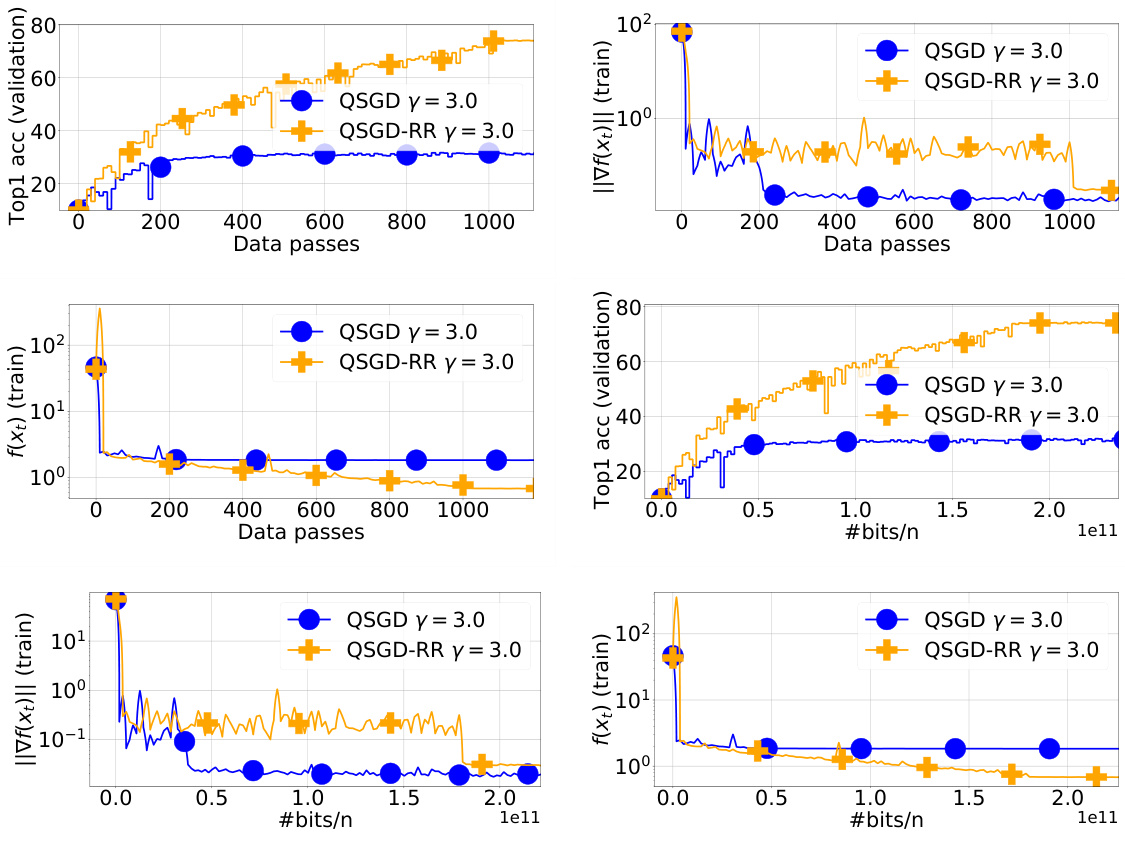
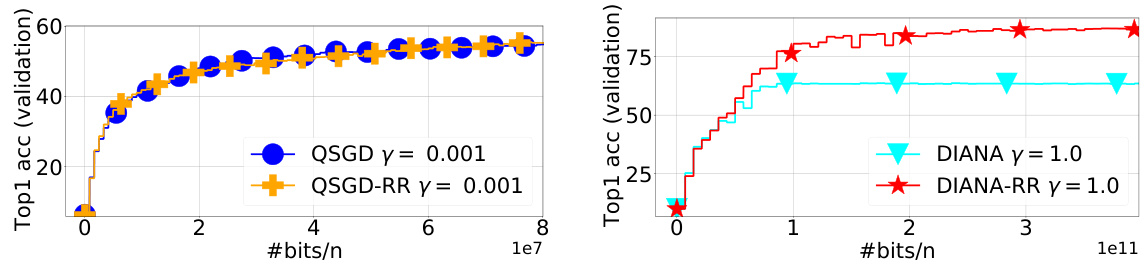
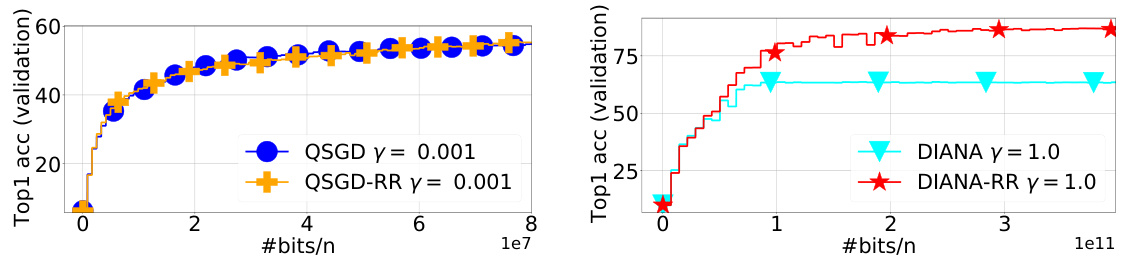
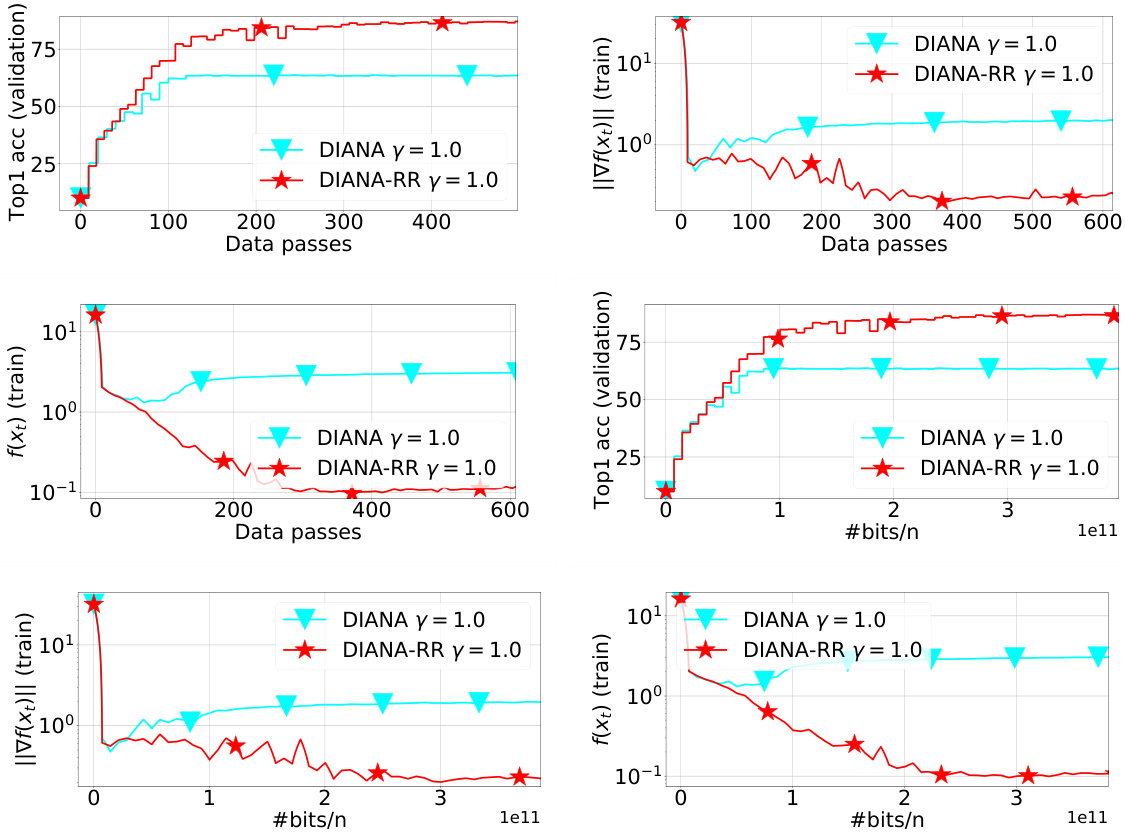
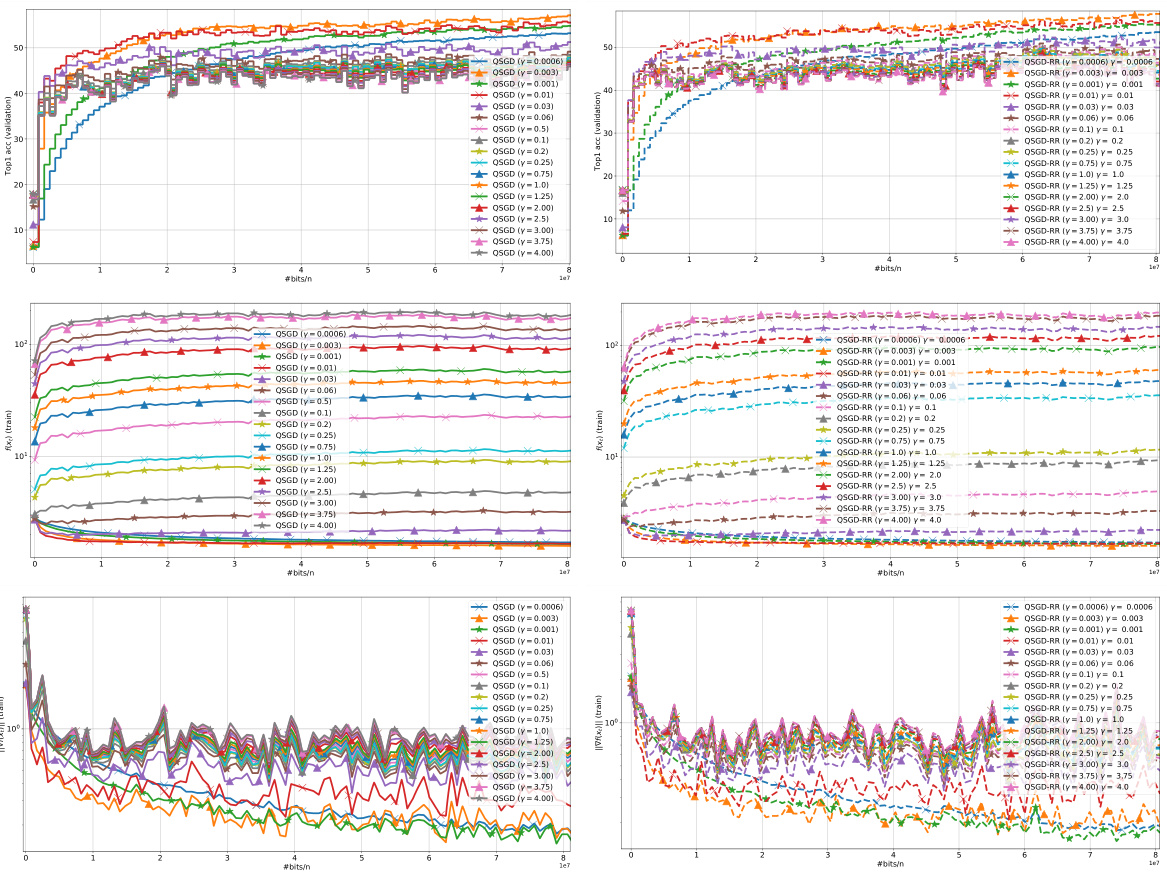
This figure compares the performance of QSGD and Q-RR on the ResNet-18 model trained on the CIFAR-10 dataset using 10 workers. It displays Top-1 accuracy on the test set, the norm of the full gradient on the training set, and the loss function value on the training set. The step sizes and decay shift were determined based on minimizing the loss function on the training set. The figure shows the results across various stages of training and illustrates the difference in performance between the two algorithms.
The figure compares the performance of local methods: Q-NASTYA, DIANA-NASTYA, FedCOM, and FedPAQ. The results show the training progress (f(x) - f(x*)) over data passes for three datasets: mushrooms, w8a, and a9a. Each dataset is tested with a different random reshuffling parameter (Rand-2 or Rand-6). The plot illustrates the convergence speed and stability of each algorithm across different datasets and reshuffling schemes. DIANA-NASTYA generally outperforms the other methods, suggesting the effectiveness of combining the DIANA technique with local steps and random reshuffling.
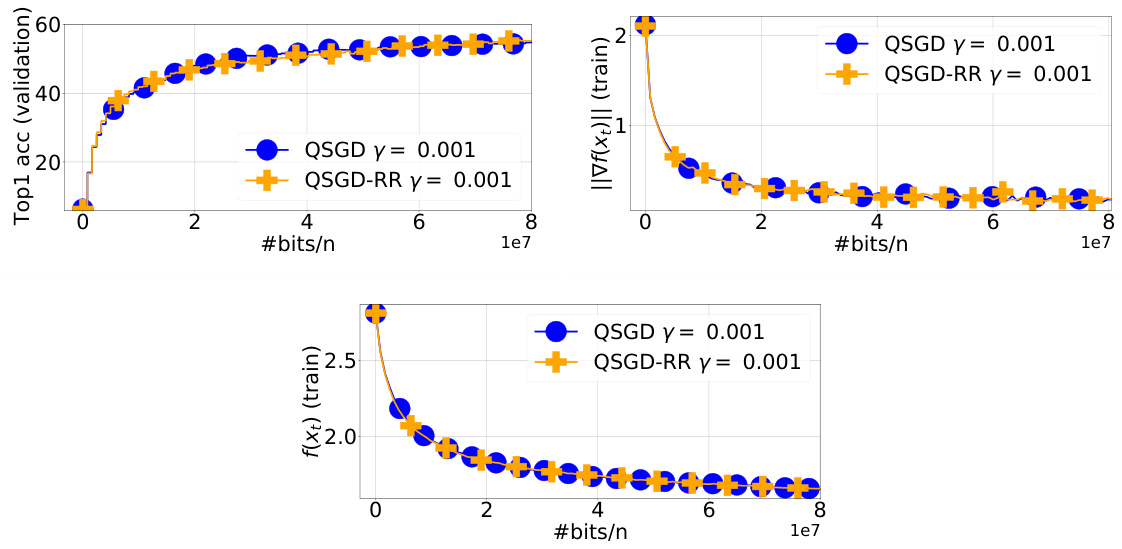
The figure compares the performance of QSGD and Q-RR algorithms on the ResNet-18 model trained on CIFAR-10 dataset. The comparison is made across three metrics: Top-1 accuracy on the test set, the norm of the full gradient on the training set, and the loss function value on the training set. The step sizes and decay shift for both algorithms were tuned based on minimizing the loss function on the training set. The results suggest that Q-RR achieves a lower loss function value and a slightly higher Top-1 accuracy compared to QSGD, indicating that Q-RR might be slightly better in terms of generalization.
The figure shows the comparison of the proposed methods (Q-NASTYA, DIANA-NASTYA, Q-RR, DIANA-RR), DIANA-RR-1S (a modification of DIANA-RR), and existing baselines (QSGD, DIANA, FedCOM, FedPAQ) for three different datasets (mushrooms, w8a, a9a). Each plot displays the training loss, f(x) - f(x*), over the number of data passes. The results illustrate the performance of these methods in a setting without local steps, showcasing their communication efficiency and convergence speed.
More on tables

This table summarizes the communication complexity of various algorithms for solving distributed finite-sum optimization problems. It compares the algorithms’ performance with and without random reshuffling and gradient compression, highlighting the impact of these techniques on communication efficiency and convergence speed under different convexity assumptions.

This table compares the communication complexity of various optimization algorithms for solving distributed finite-sum problems. It shows the number of communication rounds needed to achieve a specific accuracy (ε) for each algorithm, indicating whether they use random reshuffling (RR), gradient compression (C), have a complexity independent of data heterogeneity (H), and handle non-strongly convex functions (CVX). The table uses specific notation (K, σ²M, σ²η, σ²κ) to represent problem parameters and variance terms.

This table summarizes the time and communication complexities of various optimization algorithms for solving distributed finite-sum problems. It compares algorithms with and without random reshuffling and gradient compression, highlighting their convergence properties under different convexity assumptions and data heterogeneity levels.

This table summarizes the communication complexity of various optimization algorithms for solving distributed finite-sum problems. It compares the performance of algorithms with and without random reshuffling and gradient compression, considering different convexity assumptions and data heterogeneity. The table provides a detailed overview of existing and novel algorithms’ complexities, showing their dependence on relevant parameters such as the Lipschitz constant, strong convexity constants, variance, and the number of data samples and clients.

This table summarizes the existing and new complexity results for solving distributed finite-sum optimization problems. It compares various optimization methods based on several criteria, including whether they use random reshuffling (RR), gradient compression (C), and their dependence on data heterogeneity (H). The table also indicates if the methods assume convex but not necessarily strongly convex loss functions (CVX). Mathematical notation clarifies the complexity measures and parameters used.
Full paper#