↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Image restoration often struggles to balance detail preservation with efficient representation. Traditional autoencoders compress images in spatial domain, often losing high-frequency detail in their narrow bottleneck. This loss of detail limits their performance in tasks like super-resolution and blind image restoration, where preserving fine details is critical.
CosAE, a novel autoencoder, addresses these issues by encoding frequency domain coefficients (amplitudes and phases) instead of directly compressing spatial features. This allows for extreme spatial compression in the bottleneck without sacrificing detail. Experiments demonstrate that CosAE surpasses state-of-the-art performance in flexible-resolution super-resolution and blind image restoration, showcasing its ability to learn a powerful, generalizable representation for image restoration.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in image restoration and representation learning. It introduces a novel and highly effective Autoencoder (CosAE) that achieves state-of-the-art results in challenging tasks like super-resolution and blind image restoration. CosAE’s unique approach, leveraging learnable Fourier series, opens new avenues for developing more generalizable and detail-preserving image restoration models. This work is directly relevant to current trends in using deep learning for image processing and offers valuable insights for future research.
Visual Insights#

This figure compares a conventional autoencoder with the proposed Cosine Autoencoder (CosAE). The conventional autoencoder uses a relatively wide bottleneck, leading to potential loss of detail when compressing the input image into a lower-dimensional latent space. In contrast, CosAE leverages Fourier transform principles to encode the frequency coefficients (amplitude and phase) of the input image in its extremely narrow bottleneck. This allows for significant spatial compression without sacrificing fine-grained details upon reconstruction. A harmonic construction module (HCM) is used to expand these compressed coefficients, reconstructing the original image with high fidelity.

This table presents quantitative results for flexible-resolution super-resolution (FR-SR) on face images. It compares several models (including the proposed CosAE) across different input resolutions, evaluating performance using FID, LPIPS, PSNR, and SSIM metrics. The table is divided into sections showing results for models trained with only L1 loss and those trained with a combination of losses (indicated by ‘(G)’). A final section shows ablation study results to analyze the impact of specific design choices.
In-depth insights#
CosAE Architecture#
The CosAE architecture cleverly integrates a classical Fourier series representation with a feed-forward neural network. Instead of relying on traditional downsampling in the bottleneck layer, CosAE encodes frequency coefficients (amplitudes and phases) which are then spatially expanded via a Harmonic Construction Module (HCM) to reconstruct a series of harmonic functions. This enables extreme spatial compression in the bottleneck without sacrificing detail during reconstruction. The HCM uses learnable cosine basis functions, allowing the network to capture both global image structure and fine-grained details effectively. The decoder then takes these harmonic functions as input to reconstruct the final image. This unique combination of Fourier representation and neural networks results in a highly efficient and generalizable model for image restoration tasks, offering significant advantages over conventional autoencoder approaches.
FR-SR Experiments#
The heading ‘FR-SR Experiments’ suggests a section dedicated to evaluating a flexible-resolution super-resolution (FR-SR) method. A thoughtful analysis would expect this section to detail various experiments designed to rigorously test the FR-SR model’s capabilities. This would likely involve comparing the model’s performance against established baselines on standard benchmark datasets, perhaps using metrics such as PSNR, SSIM, and LPIPS to assess the visual quality. Key aspects to analyze would be the model’s ability to generalize across different upscaling factors and input resolutions, showcasing its flexible nature. Furthermore, an in-depth examination should explore the model’s robustness to various image degradations, possibly including noise, blur, or compression artifacts. A comprehensive evaluation might also investigate the trade-off between computational cost and performance, considering the impact of different network architectures and hyperparameter settings. The experimental setup, including datasets, evaluation metrics, and training procedures, needs to be thoroughly documented to ensure reproducibility. Finally, a detailed discussion of the results, highlighting both strengths and weaknesses of the FR-SR method, would be crucial to provide a comprehensive understanding of its capabilities and limitations.
Harmonic Encoding#
Harmonic encoding, in the context of signal processing and image representation, offers a powerful technique for encoding image data into a compact, yet informative, representation. The core idea involves decomposing an image into a set of harmonic functions, essentially representing the image as a weighted sum of sine and cosine waves of various frequencies and phases. This contrasts with traditional autoencoders that rely on spatial downsampling and subsequently upsampling, which can often lead to the loss of fine details during compression. Instead, harmonic encoding captures frequency information directly, allowing for significant compression without sacrificing image quality. This is achieved by representing the image in the frequency domain, specifically learning the amplitudes and phases of the harmonic components, which can be compactly encoded. A crucial advantage is the method’s ability to handle arbitrary resolutions, making it highly adaptable to flexible super-resolution tasks. The learnable harmonic functions provide a powerful tool for image restoration because they effectively represent both global structure and fine details; this is because the basis functions of different frequencies contribute differently to the details of the images. However, challenges remain in effectively representing high-frequency information and managing computational complexity when dealing with high-resolution images.
Ablation Study#
An ablation study systematically removes components of a model to assess their individual contribution. Its primary goal is to understand the impact of each component on overall performance. By isolating the effect of each part, researchers can identify crucial elements, pinpoint areas for improvement, and gain a deeper understanding of the model’s architecture and functionality. A well-designed ablation study should be methodical and controlled, varying only one component at a time while keeping others constant. This rigorous approach strengthens the conclusions and reduces the ambiguity of results. Results are typically presented quantitatively, showing performance metrics for the full model and various ablated versions. This allows for a direct comparison and highlights the importance of specific components to the overall model effectiveness. A key strength of ablation studies lies in their ability to provide insights into the model’s internal mechanisms, ultimately contributing to better model design and interpretability. However, ablation studies aren’t without limitations. The interpretation of the results can be nuanced and might be influenced by the interactions between components. A thoughtful ablation study carefully addresses these limitations and acknowledges potential confounding factors.
Future Works#
A promising avenue for future work is exploring the application of CosAE to a broader range of image restoration tasks, such as denoising, deblurring, and inpainting. Investigating the effectiveness of CosAE with different types of basis functions beyond cosine, such as sine or wavelet bases, could reveal improved performance or suitability for specific image characteristics. Furthermore, a deeper analysis of the frequency learning mechanism within CosAE is warranted, potentially optimizing the learning process and potentially leading to more robust and stable model training. The development of a more efficient implementation is crucial, especially for high-resolution images, to improve inference speed and make the method applicable to real-time applications. Finally, comparing CosAE’s performance against other state-of-the-art methods on a wider array of benchmark datasets would offer a more comprehensive evaluation and highlight its strengths and limitations more clearly.
More visual insights#
More on figures

This figure illustrates the architecture of CosAE. It shows how an input image is processed by the encoder to produce a narrow bottleneck representation. The bottleneck vector is then used by the harmonic construction module (HCM) to generate a set of harmonic functions which are then decoded to reconstruct the output image.

This figure compares the performance of different super-resolution models on face images. The input is a low-resolution 32x32 image, upsampled to 256x256 (8x). The models compared are LIIF (a state-of-the-art model), and CosAE with and without the cosine basis. The ground truth is also shown for comparison. The figure demonstrates CosAE’s ability to produce high-quality super-resolution images.

This figure compares the performance of CosAE with LIIF on the task of flexible resolution super-resolution (FR-SR) on the DIV2K dataset. It shows 8x upscaling results for two different image types: a building and a food scene. The comparison highlights CosAE’s ability to reconstruct fine details and textures more accurately than LIIF, especially in complex scenes.

This figure compares the performance of CosAE against other state-of-the-art face restoration methods. Two rows of example images are shown. The top row demonstrates real-world image restoration using images from the WebPhoto-Test dataset, and the bottom row shows results from synthetically degraded images in the CelebA-Test dataset. In each case, the leftmost image shows the input (degraded) image, followed by results from GFPGAN, RestorFormer, CodeFormer, and finally, CosAE. This allows for a visual comparison of the performance of CosAE against its competitors in recovering fine details and restoring natural-looking facial features.

This figure compares the performance of CosAE and LDM on a 4x super-resolution task using images from ImageNet. The results demonstrate that CosAE produces images with more detail and finer textures compared to LDM, particularly in areas with complex structures.
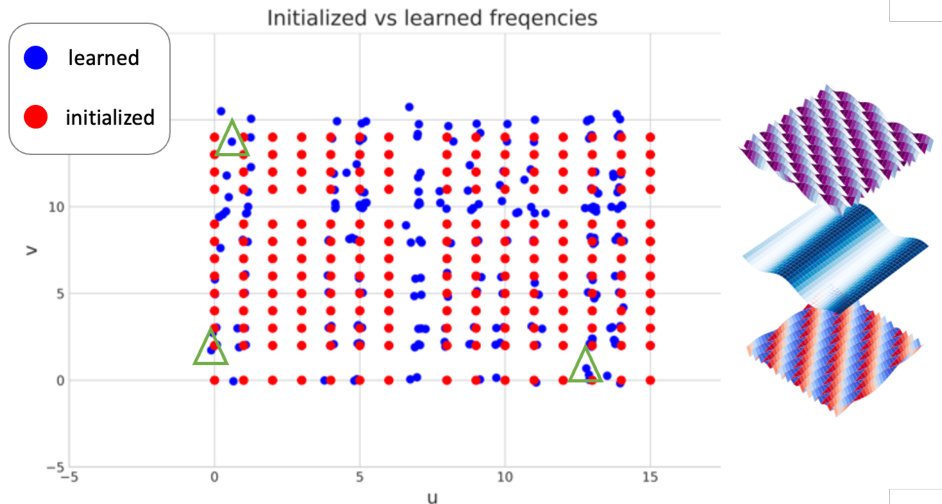
This figure compares a conventional autoencoder with the proposed Cosine Autoencoder (CosAE). The conventional autoencoder uses a relatively wide bottleneck in its latent space, which can lead to loss of detail during reconstruction. CosAE, on the other hand, uses an extremely narrow bottleneck but encodes the frequency domain coefficients (amplitudes and phases) of the input image. This allows for extreme spatial compression without losing detail upon decoding. The basis construction module helps expand these compact coefficients into a series of harmonic functions that faithfully represent both the global structure and fine-grained details of the input image before reconstruction by the decoder.

This figure illustrates the architecture of the CosAE model. The input image is first compressed by an encoder into a narrow bottleneck representation. Each element in the bottleneck represents a pair of amplitude and phase values for a specific frequency. These frequency parameters are used by a harmonic construction module (HCM) to generate spatially expanded harmonic functions using a set of cosine basis functions. Finally, the expanded functions are fed into a decoder to reconstruct the original input image.

This figure compares the performance of three different models (LIIF-4x, LIIF-32x, and CosAE) on the task of super-resolution using the DIV2K dataset. It demonstrates the advantage of using narrow bottlenecks in autoencoders for image restoration. The images show that with a narrow bottleneck (LIIF-32x and CosAE), the quality of the upscaled image remains consistent regardless of whether the upscaling factor is 2x or 8x. However, with a wide bottleneck (LIIF-4x), the quality is better with lower upscaling factor (2x) and worse at higher upscaling factors (8x). This suggests that a narrow bottleneck helps to maintain details and fidelity when upscaling the image.

This figure compares the performance of three different models (LIIF-4x, LIIF-32x, and CosAE) on the task of 8x super-resolution using the DIV2K dataset. Each row shows a different image, with the original low-resolution (LR) image in the first column, and the high-resolution (HR) results from each model in the subsequent columns. The red boxes highlight specific regions for closer examination of the detail and quality of the super-resolution results.

This figure shows a qualitative comparison of face super-resolution results using different models. It demonstrates the ability of CosAE to achieve high-resolution output (256x256) from low-resolution input (32x32) images, significantly outperforming other methods (LIIF). The figure also showcases the performance of CosAE variations, as compared to the standard CosAE and LIIF.

This figure shows a qualitative comparison of face super-resolution results using different methods. It highlights the ability of CosAE to achieve high-resolution results (256x256) from extremely low-resolution input (32x32). The comparison includes LIIF and various versions of CosAE to demonstrate the effectiveness of the proposed approach.

This figure compares the CosAE model’s performance against other state-of-the-art face restoration methods on both synthetically and realistically degraded images. Each row shows examples of different degradation types (median, server, light, synthetic). The results demonstrate CosAE’s ability to restore high-quality images even under various degradation conditions.

This figure compares the performance of CosAE and LIIF on DIV2K dataset for 8x super-resolution. CosAE shows better performance with more fine-grained details preserved in the reconstructed images, especially in close-ups.

This figure compares the performance of three different models (LIIF-4x, LIIF-32x, and CosAE) on a super-resolution task using the DIV2K dataset. The leftmost column shows the low-resolution input images. The other columns display the super-resolved images generated by each model. The figure showcases the ability of the CosAE model to generate high-quality super-resolved images with a high degree of detail preservation, especially in close-ups, compared to the other two models.

This figure compares the results of 4x super-resolution on ImageNet images using CosAE and LDM. It visually demonstrates that CosAE produces images with more refined details and textures compared to LDM. The zoomed-in view emphasizes the superior quality of the CosAE results.

This figure shows the results of applying the CosAE model to perform 8x super-resolution on natural images from the DIV2K dataset. The left side displays the low-resolution input image, and the right side shows the corresponding high-resolution output produced by CosAE. The image demonstrates the model’s ability to restore fine details and textures in a natural image, even at a significant upscaling factor.

This figure shows the result of blind face image restoration using CosAE. The left side shows the input image, which is a low-resolution and degraded image. The right side shows the restored image produced by CosAE. The restoration is performed at 512x512 resolution, demonstrating CosAE’s ability to recover high-quality image details from significantly degraded input.

This figure shows the result of blind face image restoration using CosAE. The left half shows a blurry, low-quality image, while the right half depicts the restored image using CosAE, achieving significantly improved clarity and detail in the 512 x 512 resolution.

This figure shows a qualitative comparison of blind face image restoration results using CosAE. The left half of the image shows a noisy or degraded input image, while the right half shows the corresponding restored image produced by CosAE. The resolution of both images is 512 × 512 pixels. The example demonstrates CosAE’s ability to recover details and enhance the overall quality of a degraded face image.
More on tables

This table presents a quantitative comparison of different super-resolution (SR) models on face images from the FFHQ and CelebA datasets. The models are evaluated on their ability to upscale low-resolution (LR) images to a 256x256 resolution. The table includes metrics such as FID, LPIPS, PSNR, and SSIM, which assess different aspects of image quality. Results are shown for different LR input resolutions and for models trained with either just L1 loss or with a full set of objectives. The bottom section shows ablation study results for the CosAE model.

This table presents a quantitative comparison of different methods for flexible-resolution super-resolution (FR-SR) on face images. It shows results using different input resolutions upscaled to 256x256. The methods are evaluated using FID, LPIPS, PSNR, and SSIM metrics. The table is divided into sections showing results with only L1 loss and results with full objectives (including a GAN loss). A final section shows ablation study results.

This table presents a quantitative comparison of different flexible-resolution super-resolution (FR-SR) models on the FFHQ+CelebA face dataset. The models are evaluated based on their ability to upscale low-resolution (LR) images to 256x256 high-resolution (HR) images, starting from different LR resolutions (32x32, 48x48, 64x64, 128x128). The evaluation metrics include FID, LPIPS, PSNR, and SSIM. The top section shows results using only L1 loss, while the bottom section displays results using a combination of losses (denoted by (G)). A separate section shows results from ablation studies.

This table presents a quantitative comparison of different Flexible Resolution Super-Resolution (FR-SR) methods on face images from the FFHQ and CelebA datasets. It evaluates the performance using FID, LPIPS, PSNR, and SSIM metrics for various input resolutions upscaled to 256x256. The table is divided into sections showing results with only L1 loss and results with full objectives (L1 loss + perceptual loss + GAN loss). The bottom section provides ablation study results focusing on design choices within the CosAE model.
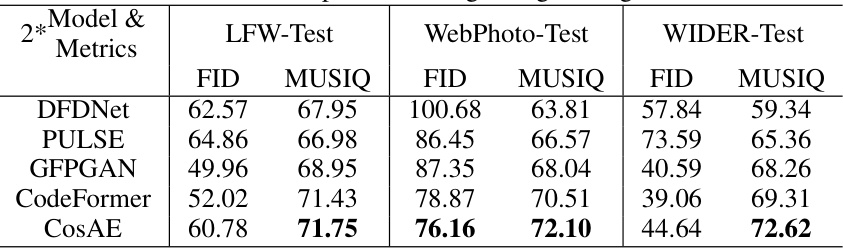
This table presents a quantitative comparison of different flexible resolution super-resolution (FR-SR) models on a face image dataset. The results are evaluated using FID, LPIPS, PSNR, and SSIM metrics for various low-resolution input sizes upscaled to 256x256. The table includes results using only L1 loss and results using a combination of L1 loss and other loss functions. A section at the bottom of the table is dedicated to ablation studies which analyze the impact of specific components of one of the models.

This table presents a quantitative comparison of different Flexible Resolution Super-Resolution (FR-SR) methods on the FFHQ+CelebA face dataset. The results are reported using FID, LPIPS, PSNR, and SSIM metrics. The table considers models trained with only L1 loss and those trained with additional objectives (denoted with (G)). The lower section displays results from ablation studies, evaluating the impact of specific design choices in the CosAE model.
Full paper#



















