↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat
TL;DR#
Current large language models (LLMs) show limitations in mathematical problem-solving. While LLMs possess reasoning capabilities, they lack explicit knowledge about their own problem-solving strategies (metacognition). This research investigates whether LLMs possess metacognitive knowledge and whether it can be harnessed to improve LLM performance. The lack of fine-grained understanding of LLMs’ reasoning processes limits effective pedagogy and training methods.
This paper proposes a novel method to extract and utilize LLMs’ metacognitive knowledge to improve mathematical problem-solving. The method involves prompting LLMs to label math problems with fine-grained skills, then clustering them into broader skill categories. These skills and their corresponding examples are used as in-context prompts, significantly enhancing various LLMs’ performance on benchmark math datasets. The methodology is domain-agnostic, thus applicable beyond math problems.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel approach to understanding LLMs’ cognitive processes by leveraging their metacognitive abilities. It demonstrates how to improve LLMs’ mathematical problem-solving skills by prompting them with contextually relevant examples based on the skills identified by the LLMs themselves. This opens exciting new avenues for research into more effective LLM training and prompting techniques, potentially leading to significant advancements in various AI tasks.
Visual Insights#
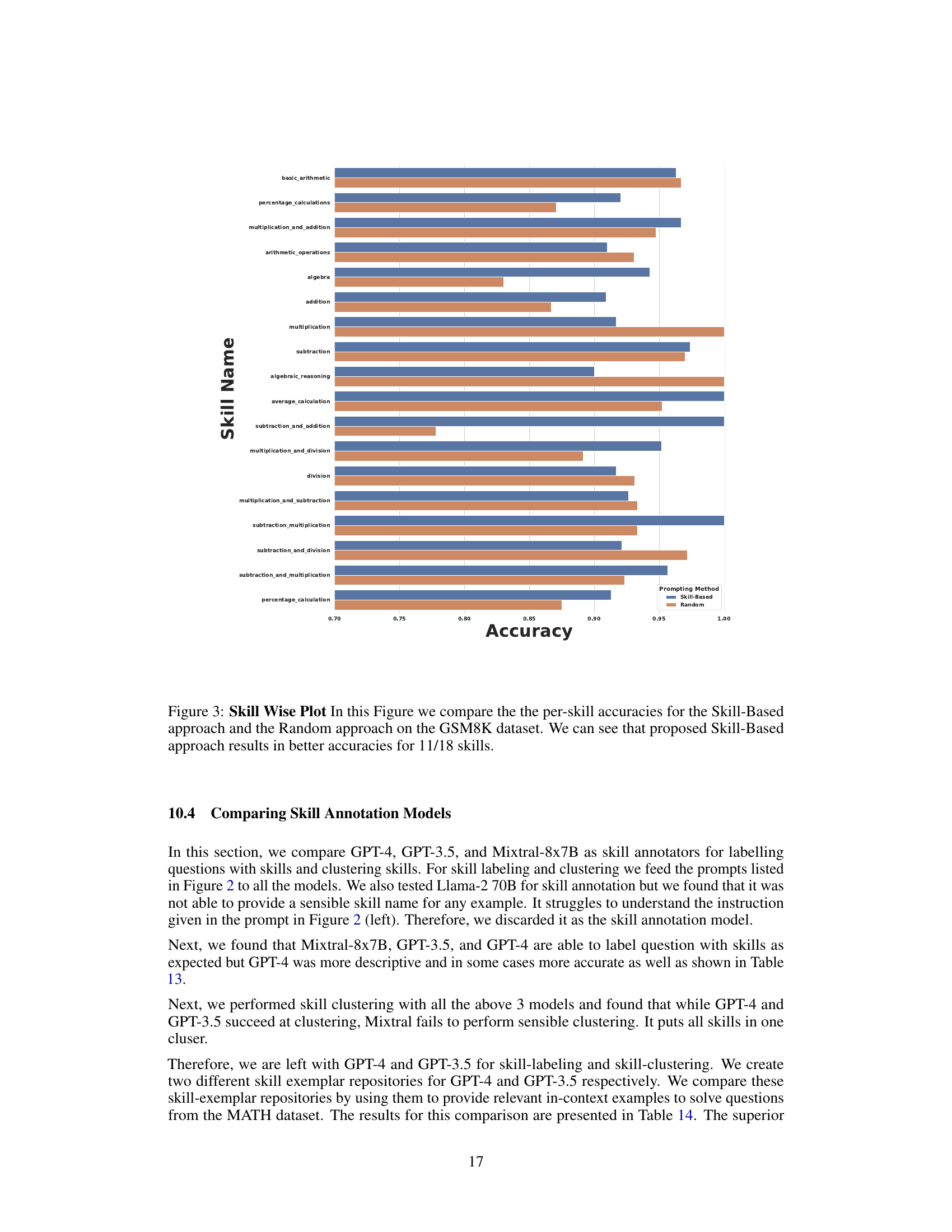
This figure illustrates the process of creating a skill exemplar repository using an LLM. It involves three main stages: skill labelling, skill clustering, and the creation of the repository itself. During inference, the LLM uses the repository to identify relevant skills and select in-context examples to help solve new questions.

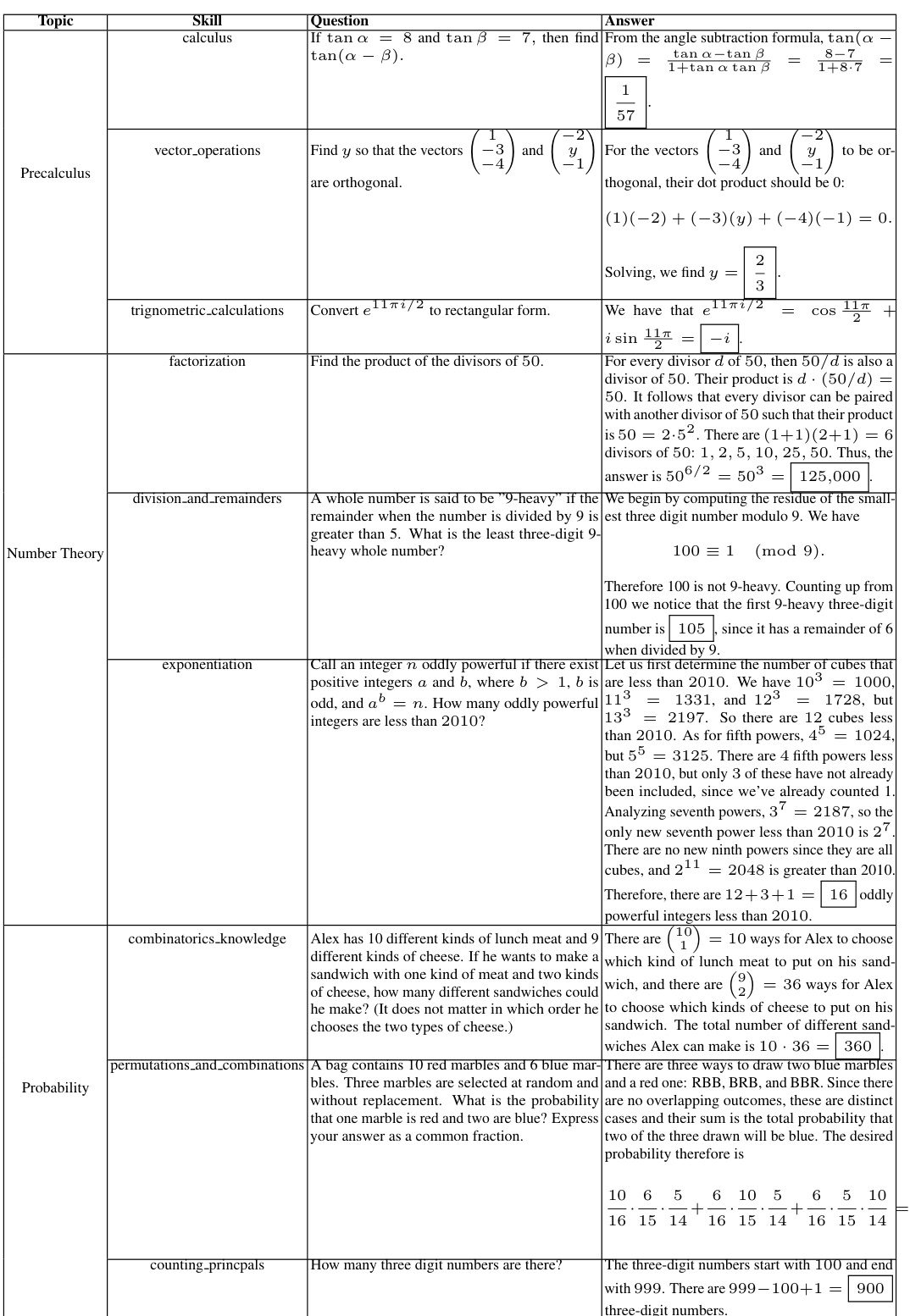
This table shows the list of skills obtained after the skill clustering phase for GSM8K and MATH datasets. The skills are categorized by topic and were generated by GPT-4. A more complete list for the MATH dataset is available in the appendix.
In-depth insights#
LLM Metacognition#
The concept of “LLM Metacognition” explores whether large language models (LLMs) possess a form of self-awareness regarding their own reasoning processes. While LLMs don’t experience consciousness like humans, they exhibit behaviors suggestive of metacognitive abilities. This research investigates this by prompting LLMs to label the skills needed to solve mathematical problems, then clustering these skills and using them to improve LLM performance. The success of this approach indicates that LLMs implicitly possess a catalog of internal skills, enabling them to select relevant approaches. However, the study also reveals limitations, highlighting the need for further research to better understand the nature of LLM metacognition and its relationship to human-like reasoning. The methodology is domain-agnostic, implying potential applications beyond mathematical problem solving. Future research could explore the boundaries of LLM metacognition by testing more complex tasks and examining transferability across models.
Skill-Based Prompting#
Skill-based prompting represents a significant advancement in leveraging LLMs for complex tasks. By identifying and categorizing the underlying skills required to solve a problem, this method moves beyond simple keyword matching or chain-of-thought prompting. Instead of relying on general examples, it provides the LLM with highly relevant, skill-specific examples, significantly improving performance. This approach not only enhances accuracy but also provides valuable insights into the LLM’s cognitive processes, essentially uncovering its internal “skillset.” The methodology demonstrates impressive improvements across multiple datasets and LLM models, highlighting its generalizability and robustness. Further research should explore the scalability of this method for increasingly complex tasks, as well as the potential for integrating it with other prompting techniques for synergistic effects. The domain-agnostic nature is promising, indicating the potential for broad applicability beyond mathematical problem-solving.
Automated Skill Discovery#
The section on “Automated Skill Discovery” details a novel method for identifying and organizing the skills LLMs implicitly utilize when solving mathematical problems. The core innovation is using a powerful LLM (like GPT-4) to label math problems with specific skills, then clustering similar skills to create a more manageable, human-interpretable skill set. This process generates a “Skill Exemplar Repository”, a catalog of skills and corresponding example problems. This repository facilitates in-context learning for other LLMs by providing relevant example questions during inference. The method’s strength lies in its domain agnosticism; while applied to mathematics, the underlying approach can be generalized to other problem-solving domains. The resulting enhancement in solving accuracy for various LLMs, including those with code-generation capabilities, underscores the effectiveness and transferability of the methodology. This approach moves beyond simple topic-based categorization, providing a more nuanced understanding of how LLMs reason, which has important implications for enhancing their capabilities and developing more effective pedagogical approaches.
Cross-LLM Transfer#
Cross-LLM transfer in the context of metacognitive skills focuses on the generalizability of skills learned by one large language model (LLM) when applied to others. The core idea is that if a powerful LLM can identify and categorize relevant skills for solving mathematical problems, this knowledge can be transferred to less capable LLMs, enhancing their problem-solving abilities. This is achieved by using the skill labels and exemplars generated by the powerful LLM to guide the less capable models. The success of cross-LLM transfer depends on the meaningfulness and relevance of the skill labels identified, as well as the domain-agnostic nature of the skill categorization process. The experiments should thoroughly investigate the effectiveness of this transfer across various LLMs and datasets, demonstrating improved performance in the less capable models. A successful demonstration would highlight the potential of leveraging metacognitive knowledge from a strong LLM to improve the capabilities of a wider range of models, suggesting a powerful new approach to LLM training and development.
Future Directions#
Future research could explore several promising avenues. Extending the methodology to other domains beyond mathematics is crucial to demonstrate its broad applicability and assess the generalizability of LLM metacognitive skills. Investigating the impact of multiple skills per question will refine the skill exemplar repository, leading to more accurate and nuanced LLM skill identification. Addressing the limitations of applying the approach to weaker LLMs and exploring techniques to enhance their performance warrants further investigation. Finally, research into the integration of the Skill-Based approach with various prompting methods will offer a more powerful and versatile framework for LLM-based reasoning. Further study should also focus on the potential for skill knowledge transfer to improve model fine-tuning, a potentially groundbreaking area.
More visual insights#
More on figures

This figure illustrates the process of creating a Skill Exemplar Repository. The process involves three main stages: (1) Skill Labelling: an LLM assigns fine-grained skill labels to individual questions; (2) Skill Clustering: the LLM groups similar skills into broader categories; and (3) Inference: during inference, the LLM uses the repository to identify relevant skill exemplars for a given test question, incorporating these as in-context examples for improved accuracy.
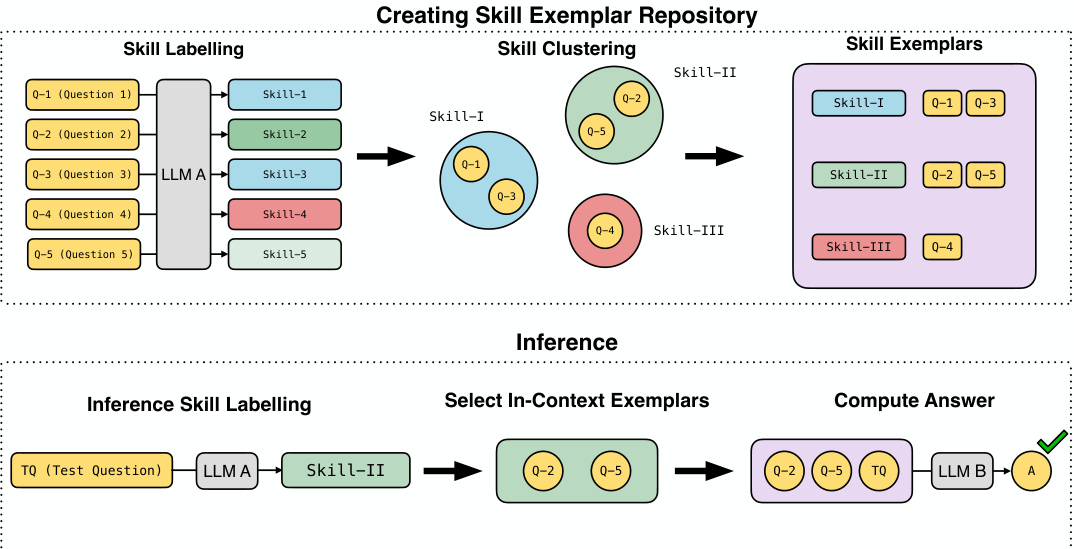
This figure illustrates the process of creating a skill exemplar repository. First, an LLM assigns fine-grained skill labels to questions. Then, it groups similar skills into broader categories. Finally, it creates a repository containing skill names and corresponding question-answer examples. During inference, the LLM identifies the relevant skill for a new question and uses the corresponding examples from the repository as in-context examples to solve the question.
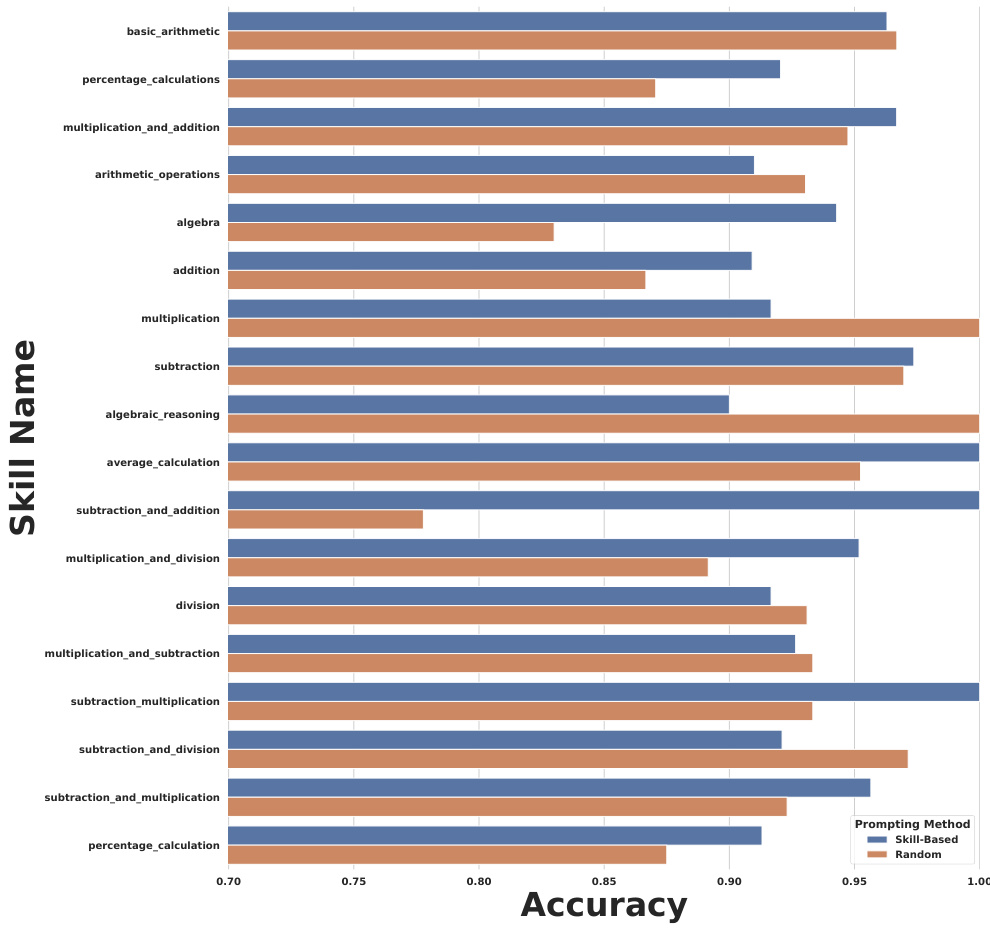
This figure illustrates the process of creating a skill exemplar repository. The process involves an LLM first labeling questions with fine-grained skills, then clustering similar skills into broader categories, and finally creating a repository of skill exemplars (skill names and examples). During inference, the LLM uses this repository to label a test question and select relevant exemplars for in-context learning.

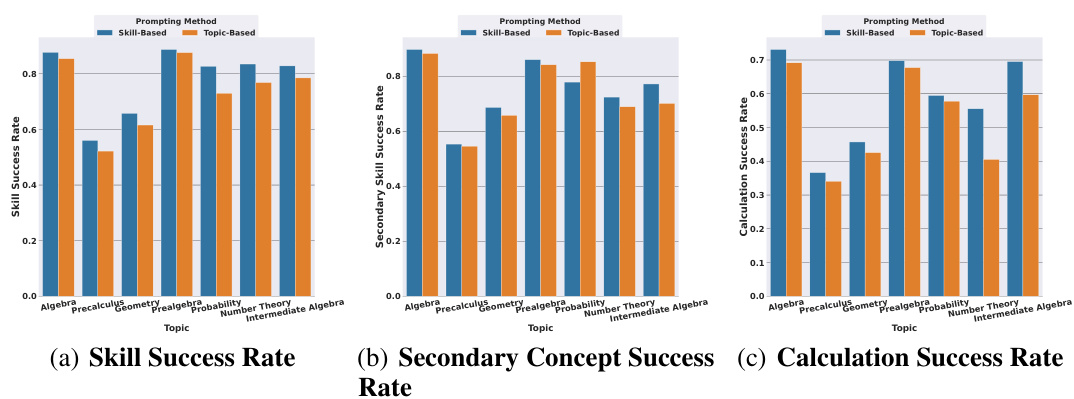
This figure illustrates the process of creating a Skill Exemplar Repository. It starts with an LLM assigning fine-grained skill labels to questions. These skills are then clustered into broader, more complex skills. A repository is built containing these coarser skills and example questions and answers. During inference, a new question is labeled with a skill, and relevant examples from the repository are used as in-context examples to help the LLM solve the question.
More on tables

This table presents the results of text-based prompting experiments conducted on the MATH dataset. It compares the performance of different prompting methods: Chain-of-Thought (CoT), Complex CoT, CoT with topic-based examples, and CoT with skill-based examples. The skill-based approach, using chain-of-thought prompting, shows the best overall performance across all mathematical topics in the dataset. All experiments utilized GPT-4-0613.

This table presents the results of text-based prompting experiments conducted on the GSM8K dataset using two different language models: GPT-3.5-Turbo and GPT-4-0613. The table compares the performance of several prompting methods, including Retrieval RSD, CoT (Chain of Thought), CoT + Random, CoT + Skill-Based, and CoT + Skill-Based (maj@5). The CoT + Skill-Based approaches consistently outperform the baselines, demonstrating the effectiveness of incorporating skill-based in-context examples. The (maj@5) variation represents the use of self-consistency.

This table presents the results of experiments using program-aided prompting methods on the MATH dataset. It compares the performance of a standard program-aided approach (PAL) with variations incorporating the Skill-Based method. The Skill-Based method uses skill-specific in-context examples to enhance code generation. The results show improved performance across different math topics when using the Skill-Based approach, demonstrating its effectiveness in enhancing code generation for problem-solving.

This table presents the results of experiments conducted using the Mixtral 8x7B model on the MATH dataset. It compares the performance of several prompting methods: standard Chain-of-Thought (CoT), CoT with topic-based exemplars, CoT with skill-based exemplars, and CoT with self-consistency (maj@4) using both topic and skill-based exemplars. The skill labels and exemplars are obtained from GPT-4-0613. The results highlight the improved performance and transferability of the skill-based approach.

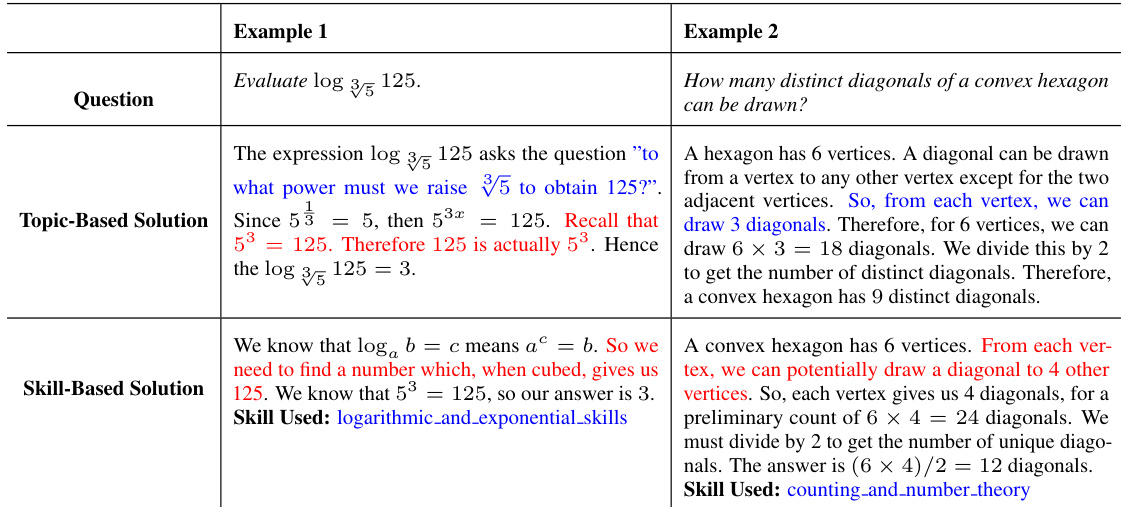
This table presents two examples where the skill-based approach outperforms the topic-based approach in solving math problems. The skill-based approach correctly identifies and applies the relevant skills, while the topic-based approach makes errors due to a misunderstanding of core concepts. The table highlights the superiority of the skill-based method for accurate and skillful problem-solving.
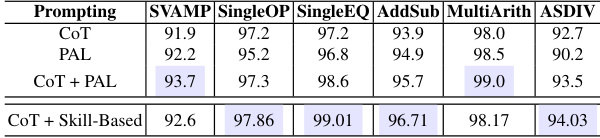
This table shows the results of applying the skill exemplars learned from the GSM8K dataset to other math word problem datasets. It demonstrates the transferability of the skill-based approach across different datasets by comparing the performance of the CoT, PAL, CoT + PAL, and CoT + Skill-Based methods on six different datasets: SVAMP, SingleOP, SingleEQ, AddSub, MultiArith, and ASDIV. The results highlight whether the skills learned from one dataset are applicable and effective in solving problems from other datasets.

This table presents the results of text-based prompting experiments on the MATH dataset. The Skill-Based approach, which uses chain-of-thought (CoT) prompting and incorporates skill-based in-context examples, is compared against several baselines (CoT, Complex CoT, CoT + Topic-Based). The results show that the Skill-Based approach achieves superior performance across all mathematical topics in the dataset, using GPT-4-0613.

This table presents the results of applying the Skill-Based approach to the alignment task using the Mistral-7B model. The performance is measured using six metrics (helpfulness, clarity, factuality, depth, engagement, and safety), each scored from 1 to 5 by GPT-4. The Skill-Based approach shows improvements across all six metrics compared to a random baseline.

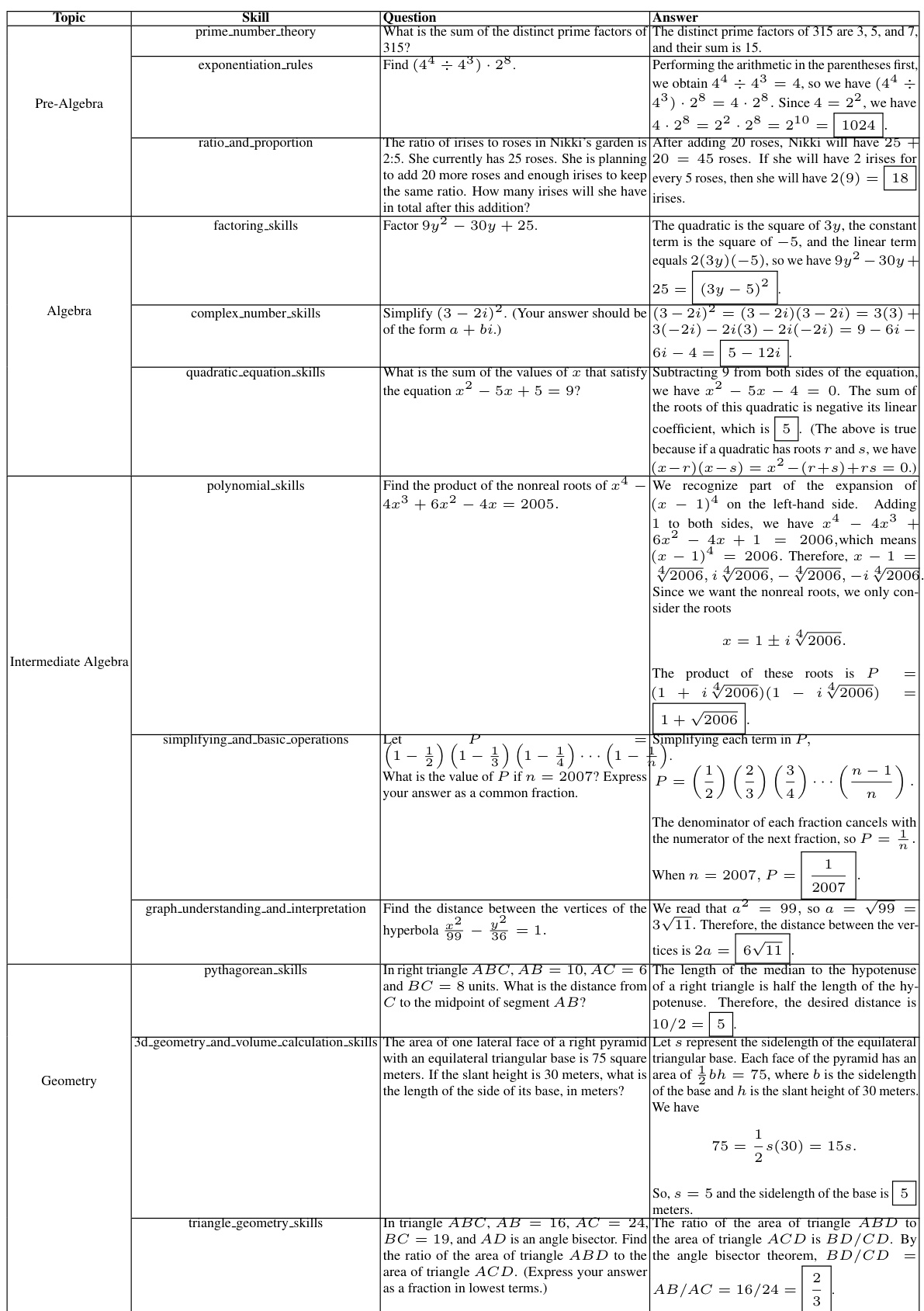
This table shows the list of skills obtained after performing skill clustering on GSM8K and MATH datasets. Each topic within the datasets is associated with a set of skills identified by the GPT-4 language model. The table helps to understand the granularity and types of skills the model identified for different mathematical problem categories.

This table shows example questions and their corresponding answers from the skill exemplar repository created using the GSM8K training dataset. Each example is labeled with a skill, showcasing how the LLM identifies relevant skills for each problem.

This table presents the results of text-based prompting experiments on the GSM8K dataset. It compares the performance of the Skill-Based approach against several baselines (Retrieval RSD, CoT, CoT + Random, CoT + Skill-Based), using two different language models (GPT-3.5-Turbo and GPT-4-0613). The Skill-Based approach consistently achieves higher accuracy, demonstrating the effectiveness of using skill-aligned in-context examples.
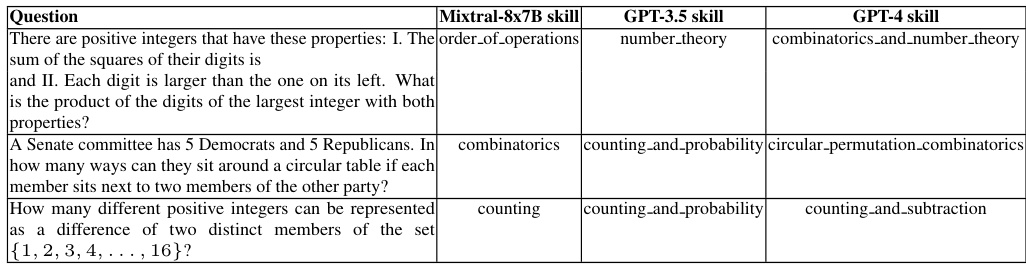
This table compares the skill labels assigned by three different language models: Mixtral-8x7B, GPT-3.5, and GPT-4, for three distinct mathematical questions. It highlights the differences in the granularity and descriptive nature of the skill labels produced by each model, showcasing GPT-4’s superior ability to provide more precise and comprehensive skill assignments.

This table presents the results of text-based prompting experiments on the MATH dataset. It compares the performance of the Skill-Based approach (using Chain-of-Thought prompting) against several baselines across different mathematical topics within the dataset. The Skill-Based approach consistently outperforms the others, demonstrating the effectiveness of incorporating skill-based information into prompting strategies.
This table presents the results of text-based prompting experiments on the MATH dataset. It compares the performance of different prompting methods, including Chain-of-Thought (CoT), CoT with topic-based examples, and CoT with skill-based examples. The skill-based approach, which uses examples from the Skill Exemplar Repository created in the study, shows significantly better performance across all math topics.

This table presents the results of transferring skill exemplars from GPT-4 to the Mixtral 8x7B model for solving math problems from the MATH dataset. It compares the performance of several prompting methods, including standard Chain-of-Thought (CoT), CoT with topic-based exemplars, CoT with skill-based exemplars, and CoT with self-consistency, using both topic-based and skill-based exemplars. The results demonstrate the effectiveness of using skill-based exemplars in enhancing the performance of weaker LLMs.
This table presents the results of text-based prompting experiments conducted on the MATH dataset. The Skill-Based approach, which incorporates Chain-of-Thought (CoT) prompting and utilizes skill-aligned examples, is compared against several baselines (CoT, Complex CoT, CoT + Topic-Based). The results show the Skill-Based approach significantly outperforms the baselines across various mathematical topics within the MATH dataset. All experiments used GPT-4-0613.
This table presents the results of text-based prompting experiments on the MATH dataset. It compares the performance of different prompting methods, including Chain of Thought (CoT), CoT with topic-based examples, and CoT with skill-based examples. The Skill-Based approach, which uses the skill exemplar repository developed earlier in the paper, significantly outperforms other methods across all topics in the MATH dataset.
Full paper#