TL;DR#
Knowledge graph completion (KGC) aims to predict missing links in knowledge graphs, often represented as tensors. Tensor decomposition-based (TDB) models are effective but prone to overfitting, leading to suboptimal performance. Existing regularization methods focus on minimizing embedding norms, which is insufficient.
This paper introduces a novel regularization technique, Intermediate Variables Regularization (IVR). IVR minimizes the norms of intermediate variables during tensor computation. The authors provide theoretical analysis proving IVR’s effectiveness in reducing overfitting by promoting low trace norm of the predicted tensor. Experiments demonstrate IVR’s superior performance compared to existing methods across multiple datasets.
Key Takeaways#
Why does it matter?#
This paper is important because it proposes a novel regularization method for tensor decomposition-based knowledge graph completion models that addresses the issue of overfitting. It offers a unified view of existing models, provides theoretical analysis supporting the method’s effectiveness, and shows improved performance in experiments. This work opens new avenues for research on regularization techniques in knowledge graph completion and related fields. It is valuable to researchers seeking to improve the accuracy and generalizability of knowledge graph completion models.
Visual Insights#

🔼 This figure illustrates the concept of tensor unfolding used in the paper. The left panel shows a 3D tensor. The middle panel displays how the tensor can be represented by its mode-1, mode-2, and mode-3 fibers (i.e., vectors obtained by fixing all but one index). The right panel depicts how each set of fibers is transformed into a matrix through mode-1, mode-2, and mode-3 unfoldings. This unfolding operation is crucial for applying matrix-based techniques to tensor analysis within the framework of the proposed method.
read the caption
Figure 1: Left shows a 3rd-order tensor. Middle describes the corresponding mode-i fibers of the tensor. Fibers are the higher-order analogue of matrix rows and columns. A fiber is defined by fixing every index but one. Right describes the corresponding mode-i unfolding of the tensor. The mode-i unfolding of a tensor arranges the mode-i fibers to be the columns of the resulting matrix.
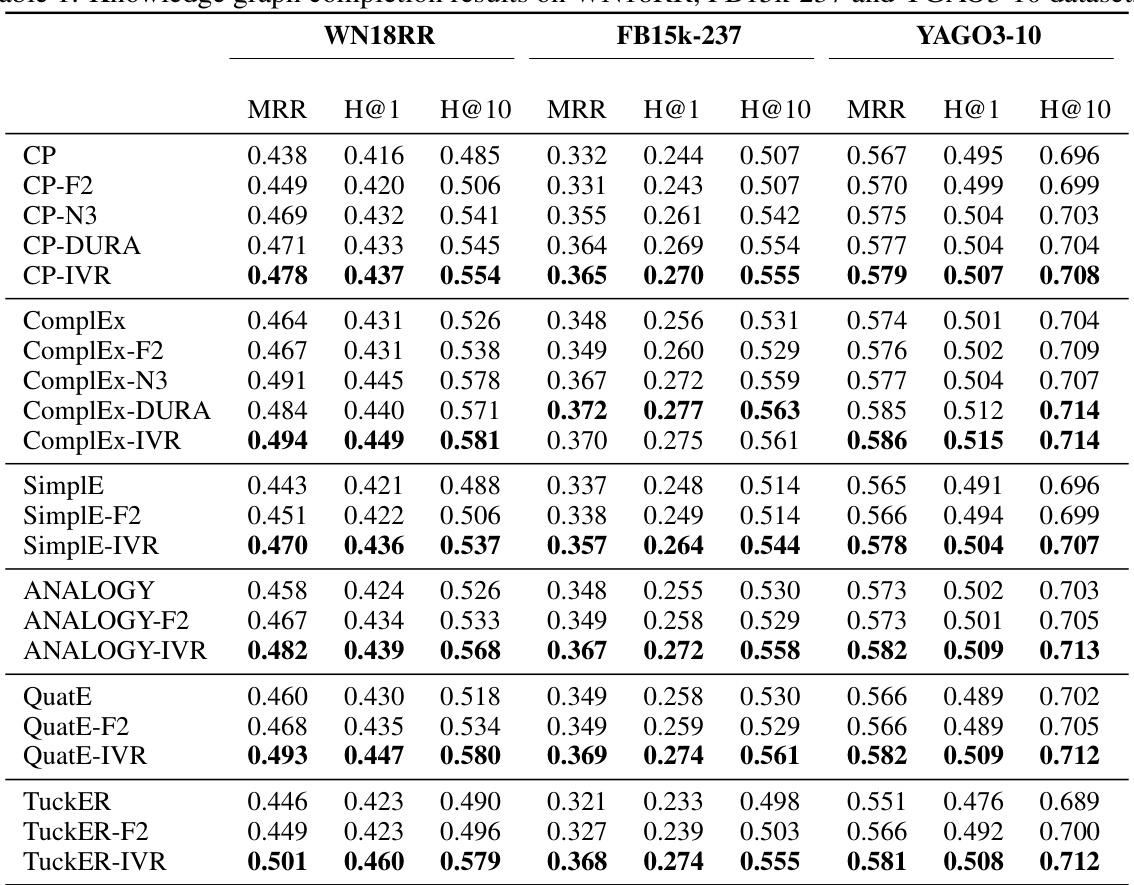
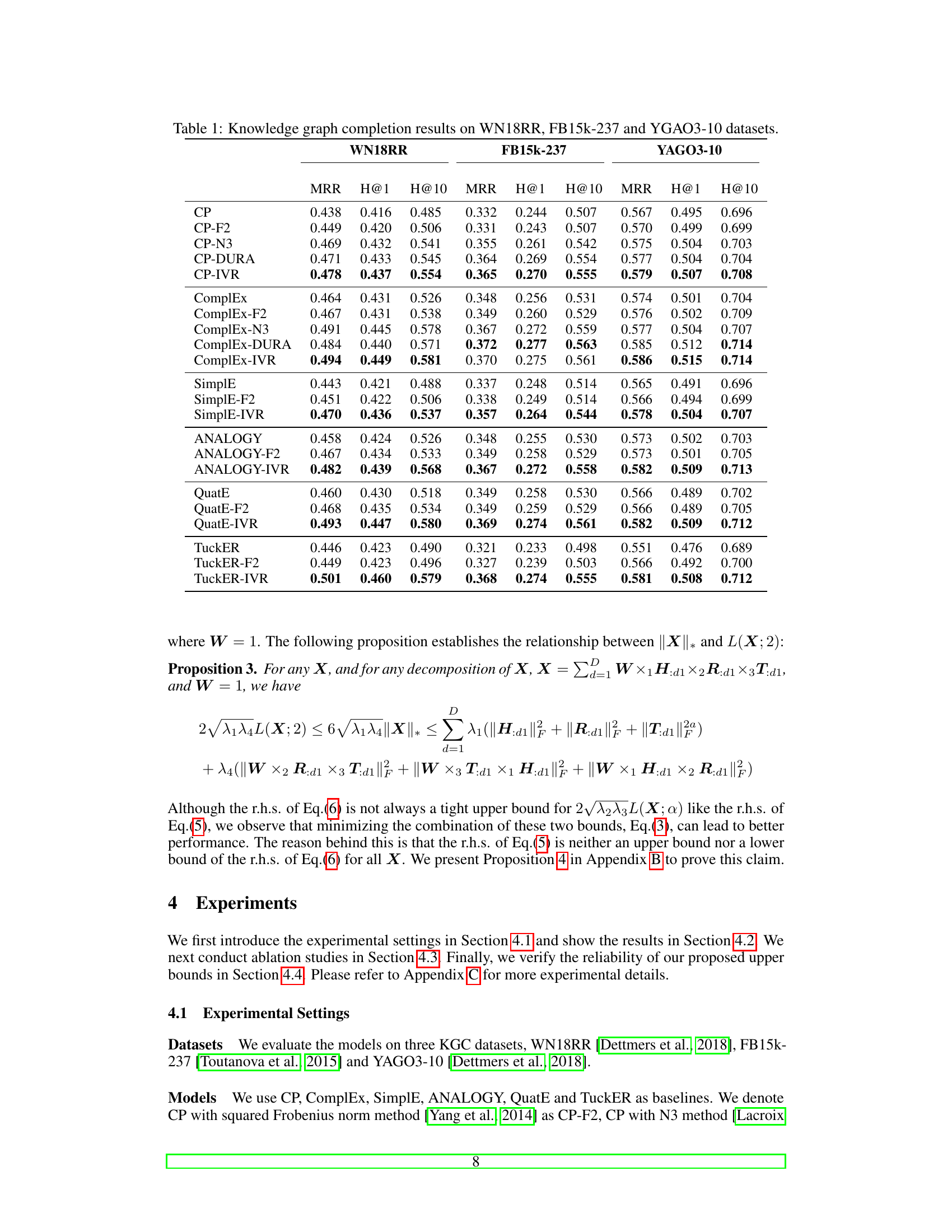
🔼 This table presents the results of knowledge graph completion experiments conducted on three benchmark datasets: WN18RR, FB15k-237, and YAGO3-10. The table compares the performance of several tensor decomposition-based models (CP, ComplEx, SimplE, ANALOGY, QuatE, TuckER) with and without different regularization techniques (F2, N3, DURA, and IVR). The metrics used to evaluate the performance are Mean Reciprocal Rank (MRR), Hits@1 (H@1), and Hits@10 (H@10). The results allow for a comparison of the effectiveness of the different models and regularization methods in completing knowledge graphs.
read the caption
Table 1: Knowledge graph completion results on WN18RR, FB15k-237 and YAGO3-10 datasets.
In-depth insights#
Tensor Decomposition#
Tensor decomposition methods are powerful tools for knowledge graph completion (KGC), offering a way to represent and reason about complex relationships within knowledge graphs. Different decomposition techniques, such as CP and Tucker decompositions, provide varying trade-offs between expressiveness and computational complexity. The choice of decomposition significantly impacts the model’s ability to capture intricate relationships and its susceptibility to overfitting. Regularization techniques are crucial to mitigate overfitting, and novel methods that go beyond simply minimizing embedding norms are actively being researched to improve performance. The general form for tensor decomposition-based models, as presented in many papers, provides a valuable foundation for understanding existing models and developing novel approaches in KGC. Future work should focus on developing computationally efficient regularization techniques and exploring the application of advanced tensor decomposition methods to enhance the accuracy and scalability of KGC systems.
IVR Regularization#
The proposed Intermediate Variables Regularization (IVR) method tackles overfitting in tensor decomposition-based knowledge graph completion (KGC) models. Instead of directly regularizing embeddings, IVR minimizes the norms of intermediate variables generated during tensor prediction. This approach is theoretically grounded, proven to bound the overlapped trace norm, thus encouraging low-rank solutions and mitigating overfitting. The method’s generality is highlighted by its applicability to various TDB models, and its practicality is demonstrated through empirical evaluation. IVR shows consistent performance improvements, outperforming existing techniques across multiple datasets, indicating its potential for enhancing the accuracy and efficiency of KGC.
Unified TDB Models#
A unified theory of tensor decomposition-based (TDB) models for knowledge graph completion (KGC) would be a significant contribution. Such a framework would systematically categorize existing models, highlighting their similarities and differences in terms of core tensor structures and decomposition strategies. This unification could lead to improved model design, enabling researchers to leverage the strengths of various approaches and address limitations more effectively. By establishing a common theoretical foundation, we can also simplify the comparative analysis of different TDB models, leading to a better understanding of their relative strengths and weaknesses. Furthermore, a unified framework would facilitate the development of novel regularization techniques, addressing prevalent overfitting issues. Generalizing regularization strategies across diverse TDB models would improve performance and promote wider applicability. Finally, this unified perspective would aid in accelerating future research on TDB models for KGC by providing a solid foundation for further innovation and exploration.
Theoretical Analysis#
A theoretical analysis section in a research paper serves to rigorously justify the claims made and validate the proposed methods. In the context of knowledge graph completion, a strong theoretical analysis might involve proving guarantees on the model’s performance or demonstrating its capacity to learn logical rules. This could involve deriving bounds on the error rate, showing that the model can represent any real-valued tensor, or exploring relationships between model parameters and the model’s ability to capture specific types of knowledge. Furthermore, a robust theoretical foundation enhances the reliability and generalizability of the findings, making the results more trustworthy. Often, a theoretical analysis will demonstrate a mathematical link between the proposed method and a known measure of goodness for the problem. For example, it might show how the approach minimizes an upper bound on the model’s trace norm, which helps to prevent overfitting. This type of theoretical contribution gives the reader much stronger confidence in the practical utility of the proposed approach.
Future Research#
Future research directions stemming from this paper could explore several promising avenues. Extending the intermediate variable regularization (IVR) technique to other knowledge graph completion (KGC) models beyond tensor decomposition-based (TDB) models is a crucial next step. This would involve adapting IVR to handle the distinct architectures and computational mechanisms of translation-based and neural network-based KGC methods. Another important direction is developing more sophisticated theoretical analyses of IVR, potentially exploring connections to other low-rank tensor norms or matrix factorization techniques. This could lead to improved regularization strategies and a deeper understanding of the method’s effectiveness. The current experimental evaluation focuses on specific benchmark datasets; investigating the performance of IVR across diverse KG datasets with varied characteristics (size, density, relational complexity) is essential to establish its robustness and generalizability. Finally, research should focus on improving the scalability of IVR for larger KGs; exploring efficient approximation algorithms or distributed computation techniques would enhance practical applicability. These research directions would significantly expand the impact and utility of IVR within the broader KGC field.
More visual insights#
More on tables
🔼 This table presents the performance of various knowledge graph completion (KGC) models on three benchmark datasets: WN18RR, FB15k-237, and YAGO3-10. The models are evaluated using the metrics Mean Reciprocal Rank (MRR), Hits@1 (H@1), and Hits@10 (H@10). For each dataset, the table shows the performance of several tensor decomposition-based models, both with and without different regularization techniques (F2, N3, DURA, and the proposed IVR). This allows for a comparison of the effectiveness of these different regularization methods on improving the performance of the underlying KGC models.
read the caption
Table 1: Knowledge graph completion results on WN18RR, FB15k-237 and YAGO3-10 datasets.
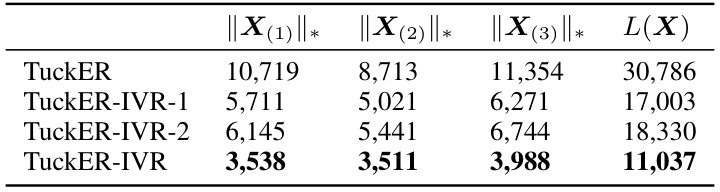
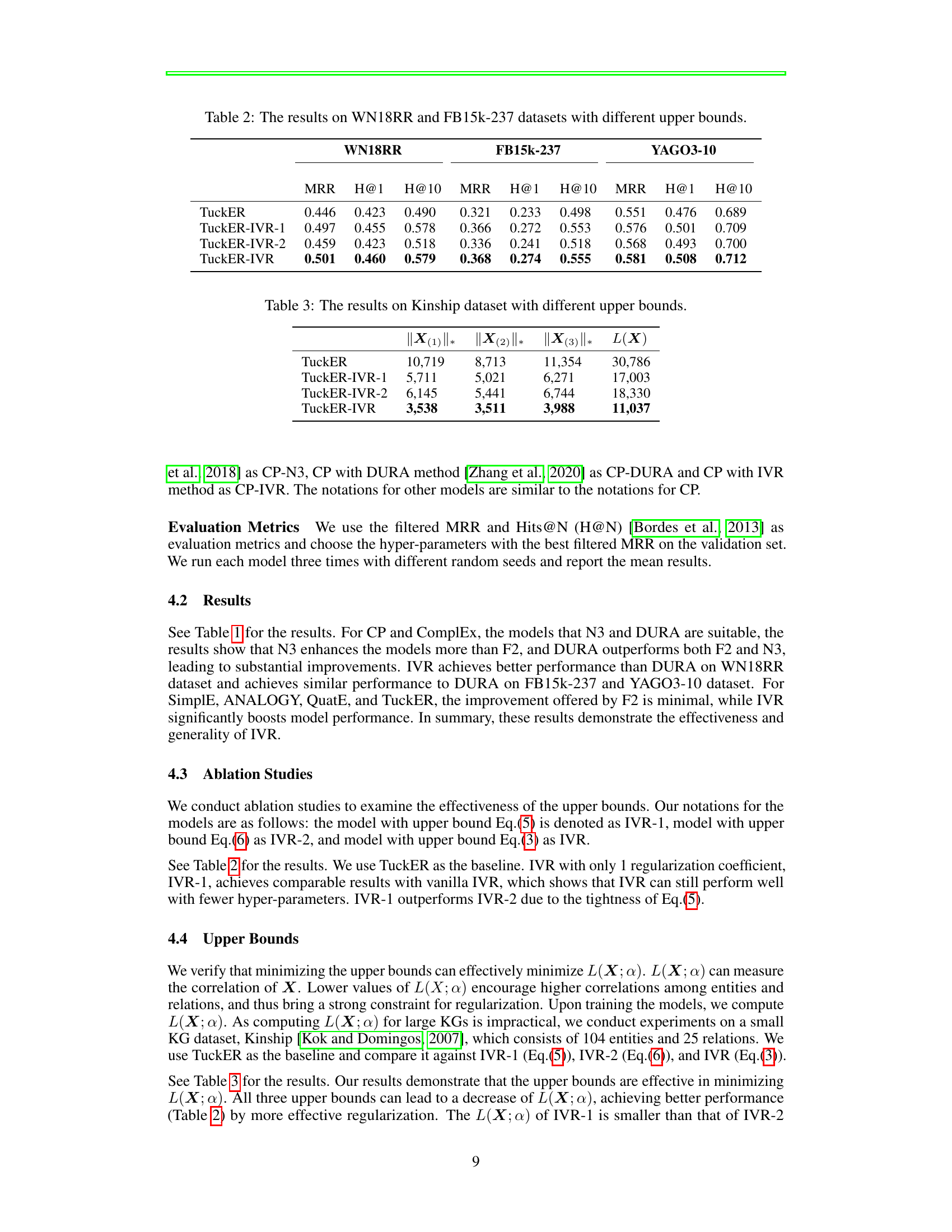
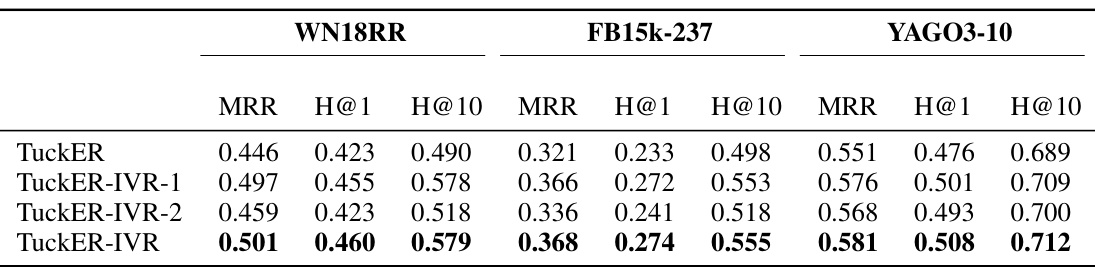
🔼 This table presents the results of experiments conducted on the Kinship dataset using the TuckER model and three variations of the proposed IVR regularization method: TuckER-IVR-1, TuckER-IVR-2, and TuckER-IVR. Each variation uses a different upper bound for the overlapped trace norm, a measure of tensor rank that reflects the correlation among entities and relations. The table shows the overlapped trace norms for each mode (||X(1)||, ||X(2)||, ||X(3)||*) and their sum L(X) for each method. The results demonstrate the effectiveness of the IVR method in minimizing the overlapped trace norm, indicating successful regularization and alleviating overfitting.
read the caption
Table 3: The results on Kinship dataset with different upper bounds.
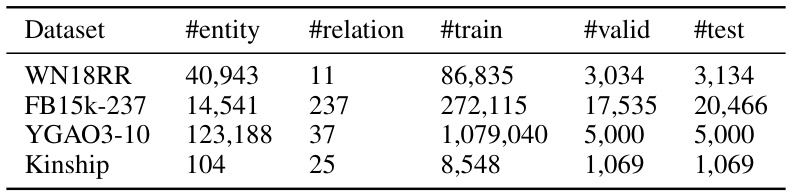
🔼 This table presents the results of knowledge graph completion experiments conducted on three benchmark datasets: WN18RR, FB15k-237, and YAGO3-10. The table compares the performance of several tensor decomposition-based (TDB) models, including CP, ComplEx, SimplE, ANALOGY, QuatE, and TuckER, with and without different regularization techniques (F2, N3, DURA, and IVR). For each model and dataset, the table reports the Mean Reciprocal Rank (MRR), Hits@1, and Hits@10, which are standard metrics for evaluating knowledge graph completion performance. These results demonstrate the relative effectiveness of different models and regularization strategies in knowledge graph completion.
read the caption
Table 1: Knowledge graph completion results on WN18RR, FB15k-237 and YAGO3-10 datasets.

🔼 This table presents the results of knowledge graph completion experiments conducted on three benchmark datasets: WN18RR, FB15k-237, and YAGO3-10. The table compares the performance of several tensor decomposition-based (TDB) models, both with and without the proposed intermediate variables regularization (IVR). The evaluation metrics used are Mean Reciprocal Rank (MRR), Hits@1 (H@1), and Hits@10 (H@10). Each row represents a different TDB model (e.g., CP, ComplEx, SimplE, ANALOGY, QuatE, TuckER), and each column shows the performance for a specific metric on one of the datasets. Variations of the models with different regularization techniques (F2, N3, DURA, and IVR) are included for comparison, demonstrating the effectiveness of the proposed IVR method.
read the caption
Table 1: Knowledge graph completion results on WN18RR, FB15k-237 and YAGO3-10 datasets.

🔼 This table presents the results of knowledge graph completion experiments conducted on three benchmark datasets: WN18RR, FB15k-237, and YAGO3-10. The table compares the performance of several tensor decomposition-based (TDB) models, including CP, ComplEx, SimplE, ANALOGY, QuatE, and TuckER, both with and without the proposed Intermediate Variables Regularization (IVR). For each model, the Mean Reciprocal Rank (MRR) and Hits@1 and Hits@10 metrics are reported, providing a comprehensive performance evaluation across different models and datasets.
read the caption
Table 1: Knowledge graph completion results on WN18RR, FB15k-237 and YAGO3-10 datasets.
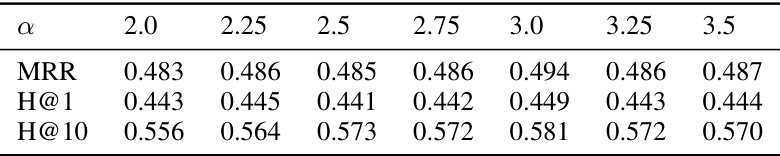
🔼 This table presents the results of knowledge graph completion experiments conducted on three benchmark datasets: WN18RR, FB15k-237, and YAGO3-10. The table compares the performance of several tensor decomposition-based (TDB) models, including CP, ComplEx, SimplE, ANALOGY, QuatE, and TuckER, both with and without the proposed intermediate variables regularization (IVR). The evaluation metrics used are Mean Reciprocal Rank (MRR), Hits@1, and Hits@10, providing a comprehensive assessment of each model’s ability to predict missing links in the knowledge graph.
read the caption
Table 1: Knowledge graph completion results on WN18RR, FB15k-237 and YAGO3-10 datasets.

🔼 The table presents the performance of different knowledge graph completion (KGC) models on three benchmark datasets: WN18RR, FB15k-237, and YAGO3-10. Each model’s performance is measured using three metrics: Mean Reciprocal Rank (MRR), Hits@1 (H@1), and Hits@10 (H@10). The table compares the performance of several tensor decomposition-based (TDB) models (CP, ComplEx, SimplE, ANALOGY, QuatE, TuckER) with and without the proposed intermediate variables regularization (IVR). The results show the effectiveness of the proposed regularization technique across various models and datasets.
read the caption
Table 1: Knowledge graph completion results on WN18RR, FB15k-237 and YAGO3-10 datasets.

🔼 This table presents the results of knowledge graph completion experiments conducted on three benchmark datasets: WN18RR, FB15k-237, and YAGO3-10. The table compares different tensor decomposition-based (TDB) models, each evaluated using three metrics (MRR, H@1, H@10). For each TDB model (CP, ComplEx, SimplE, ANALOGY, QuatE, TuckER), variations incorporating different regularization techniques (F2, N3, DURA, IVR) are also included. This allows for a comprehensive comparison of model performance with and without various regularization methods across multiple datasets.
read the caption
Table 1: Knowledge graph completion results on WN18RR, FB15k-237 and YAGO3-10 datasets.

🔼 This table presents the performance of different knowledge graph completion (KGC) models on three benchmark datasets: WN18RR, FB15k-237, and YAGO3-10. For each dataset, the table shows the mean reciprocal rank (MRR), hits@1 (H@1), and hits@10 (H@10) metrics. The models compared include various tensor decomposition-based (TDB) models (CP, ComplEx, SimplE, ANALOGY, QuatE, TuckER) with different regularization techniques (F2, N3, DURA, and the proposed IVR). The results demonstrate the comparative performance of these models with different regularization strategies.
read the caption
Table 1: Knowledge graph completion results on WN18RR, FB15k-237 and YAGO3-10 datasets.
Full paper#