Classification Diffusion Models: Revitalizing Density Ratio Estimation

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it revitalizes density ratio estimation (DRE), a powerful but previously underutilized method for learning data distributions. By overcoming limitations of existing DRE techniques, it opens new avenues for generative modeling, particularly in image synthesis, and provides a method for directly obtaining likelihoods, which is highly valuable across many machine learning tasks.

Visual Insights

#

This figure compares the image generation results of Classification Diffusion Models (CDMs) and Telescoping Density Ratio Estimation (TRE) models. The left side shows samples generated by CDMs trained on CelebA (faces) and CIFAR-10 (objects). The right side shows samples from TRE, a state-of-the-art density ratio estimation method, trained on MNIST and CIFAR-10. The figure highlights the superior performance of CDMs in generating high-quality images, especially for complex datasets like CIFAR-10, where TRE fails. This demonstrates the effectiveness of the proposed CDM method for learning high-dimensional image distributions.

This table compares the performance of a classification diffusion model (CDM) trained using different loss functions: cross-entropy (CE) only, mean squared error (MSE) only, and both CE and MSE. It demonstrates that using both CE and MSE is crucial for achieving optimal classifier performance, as measured by classification accuracy, cross-entropy loss, MSE loss, Fréchet Inception Distance (FID), and negative log-likelihood (NLL). The results highlight the importance of balancing the classification task with the denoising objective to avoid the density-chasm problem, which is a known issue in density ratio estimation methods.

In-depth insights

#

DRE Revitalized

#

The heading “DRE Revitalized” suggests a significant advancement in density ratio estimation (DRE), a technique for learning data distributions. The revitalization likely involves overcoming previous limitations of DRE, such as its inability to handle high-dimensional data like images effectively. The core idea might center on integrating DRE with a successful modern approach, like diffusion models, to enhance its capabilities. This combination could leverage the strengths of both methods, enabling DRE to capture complex distributions while retaining its valuable property of directly providing likelihoods. A key innovation may be a novel theoretical link or algorithmic framework connecting the optimal classification inherent in DRE with the denoising steps crucial to diffusion models, bridging seemingly disparate approaches. The resulting method, potentially labeled a “Classification Diffusion Model,” would demonstrate improved generative performance on complex datasets, demonstrating that DRE, once considered less relevant due to its past limitations, is now a viable and powerful technique for tackling challenging problems in machine learning. The revitalization is a notable development, not just for DRE’s direct applications, but also for its potential implications in areas such as likelihood-based evaluation of generative models, a significant challenge currently faced by prominent methods.

CDM: A New DRE

#

The heading “CDM: A New DRE” suggests a novel approach to density ratio estimation (DRE) using Classification Diffusion Models (CDMs). This implies a significant departure from traditional DRE methods, likely leveraging the strengths of diffusion models for improved performance, especially in high-dimensional spaces. CDMs might address the limitations of existing DRE techniques that struggle to accurately capture complex data distributions. The core innovation likely involves using a classifier within a diffusion model framework to estimate the density ratio, potentially offering advantages in terms of accuracy, computational efficiency, and the ability to directly output likelihoods. The approach may also tackle the ‘density-chasm’ problem inherent in many DRE methods. A key focus would likely be on demonstrating superior empirical results compared to existing DRE and generative methods, possibly including state-of-the-art performance on image generation tasks and negative log-likelihood (NLL) scores. The “New” in the title emphasizes that this isn’t merely an incremental improvement but a substantial advancement in DRE methodology, possibly providing a fresh perspective and revitalizing the field.

MMSE-Optimal Link

#

An MMSE-optimal link in the context of a research paper likely explores the connection between a Minimum Mean Squared Error (MMSE) estimator and another component of the system, possibly a classifier or a denoising process. The analysis likely demonstrates how to derive or optimize one component using insights gained from the properties of the MMSE estimator. This might involve showing that under specific conditions, an MMSE solution yields a particularly well-suited input for a subsequent classifier, or that the optimal parameters of a denoiser can be directly obtained from the MMSE-optimal solution. The core idea centers on leveraging the optimality of the MMSE framework to improve the performance of a related component, potentially revealing a fundamental relationship between different parts of the system or uncovering a novel approach to a specific task. The analysis would likely rely on mathematical derivations, assumptions regarding the statistical properties of the data and noise, and possibly experimental validation to support the theoretical findings. A practical implication might be the design of more efficient or accurate systems by leveraging this link.

Beyond MNIST

#

The phrase “Beyond MNIST” encapsulates a significant challenge and achievement in generative modeling. MNIST, a dataset of handwritten digits, served as a benchmark for years, but its simplicity limits the generalizability of models trained on it. Truly demonstrating the effectiveness of a generative model requires pushing beyond MNIST to more complex, high-dimensional datasets like CIFAR-10 or ImageNet. The ability to generate realistic images from these datasets indicates a model’s robustness and capacity to capture intricate patterns and structures within data. The success in generating images “Beyond MNIST” highlights advancements in model architecture, training techniques, and a deeper understanding of data distributions. Furthermore, the ability to not only generate samples but also accurately estimate the likelihood (probability) of an input image represents a substantial advancement over traditional generative models. This likelihood estimation is crucial for evaluating model performance and for downstream applications requiring uncertainty quantification. Generating high-quality, diverse images coupled with likelihood estimation signals a true leap forward in generative modeling, marking a transition from simple benchmarks to tackling the real-world complexity of image data.

Future of DRE

#

The future of density ratio estimation (DRE) hinges on addressing its current limitations. High-dimensional data, such as images and videos, pose a significant challenge. The density-chasm problem, where classifiers fail to capture meaningful information in high-dimensional spaces, needs innovative solutions. Bridging the gap between the optimal classifier for DRE and efficient denoising techniques, as shown by the success of classification diffusion models (CDMs), is a promising avenue. Future research should explore new architectures and training strategies, potentially leveraging advancements in deep learning and optimal transport, to improve the scalability and accuracy of DRE methods. Developing more robust noise schedules tailored for specific datasets, as well as exploring alternative loss functions, are key areas for investigation. Furthermore, developing efficient and accurate methods for likelihood estimation in DRE models remains crucial. The combination of DRE’s ability to directly output likelihoods with the recent advances in generative models could lead to powerful new methods for learning data distributions and solving inverse problems.

More visual insights

#

More on figures

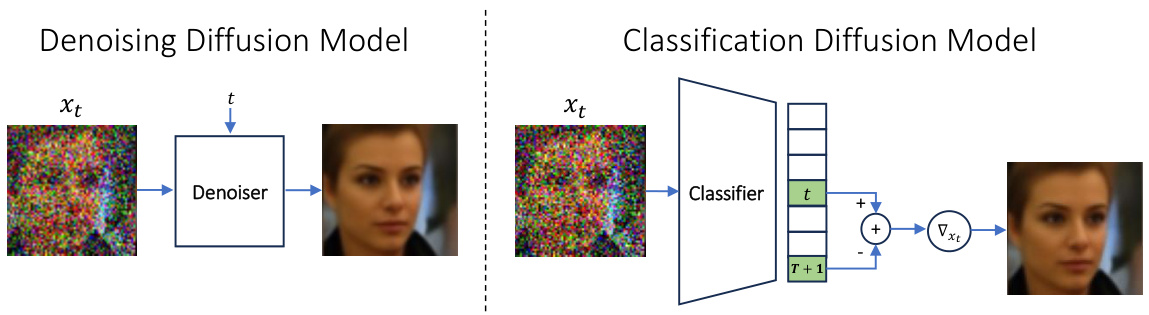
This figure illustrates the core difference between a Classification Diffusion Model (CDM) and a Denoising Diffusion Model (DDM). In a DDM, a denoiser network takes a noisy image and a timestep as input, producing a denoised image as output. In a CDM, a classifier network receives only the noisy image and outputs a probability distribution over possible timesteps indicating the amount of noise. Crucially, the CDM leverages the gradient of this probability distribution to effectively act as a denoiser, enabling it to generate images and calculate likelihoods with improved efficiency and accuracy.

This figure compares image samples generated by Classification Diffusion Models (CDMs) and the state-of-the-art density ratio estimation (DRE) method, TRE. It demonstrates that unlike previous DRE methods, CDMs are capable of generating high-quality images from complex datasets such as CelebA and CIFAR-10, showcasing their success in learning the distribution of high-dimensional data.

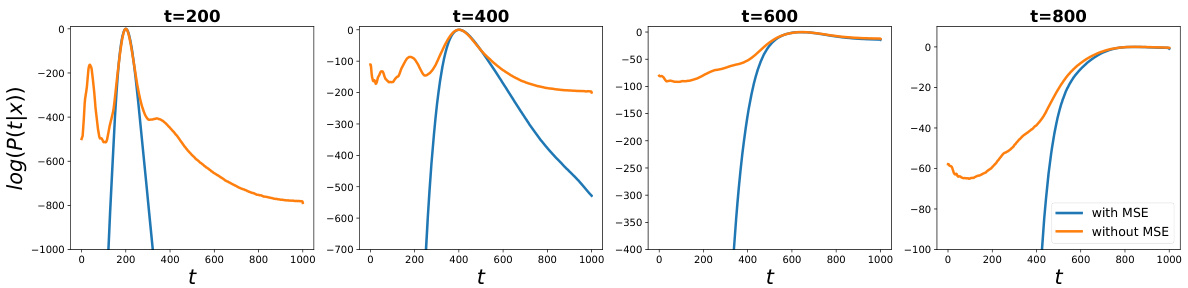
This figure compares the log probability of a noise-level classifier trained using only cross-entropy (CE) loss against one trained with both CE and mean squared error (MSE) loss. It demonstrates that using only CE loss limits the classifier’s accuracy to the correct label’s vicinity. However, incorporating MSE loss enables accurate predictions across all entries, highlighting the importance of MSE for optimal classifier performance.

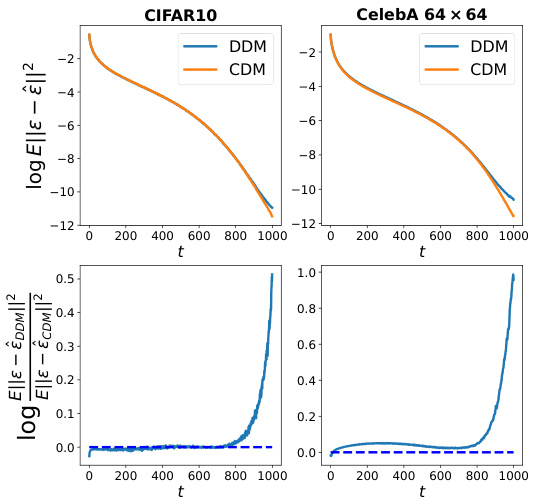
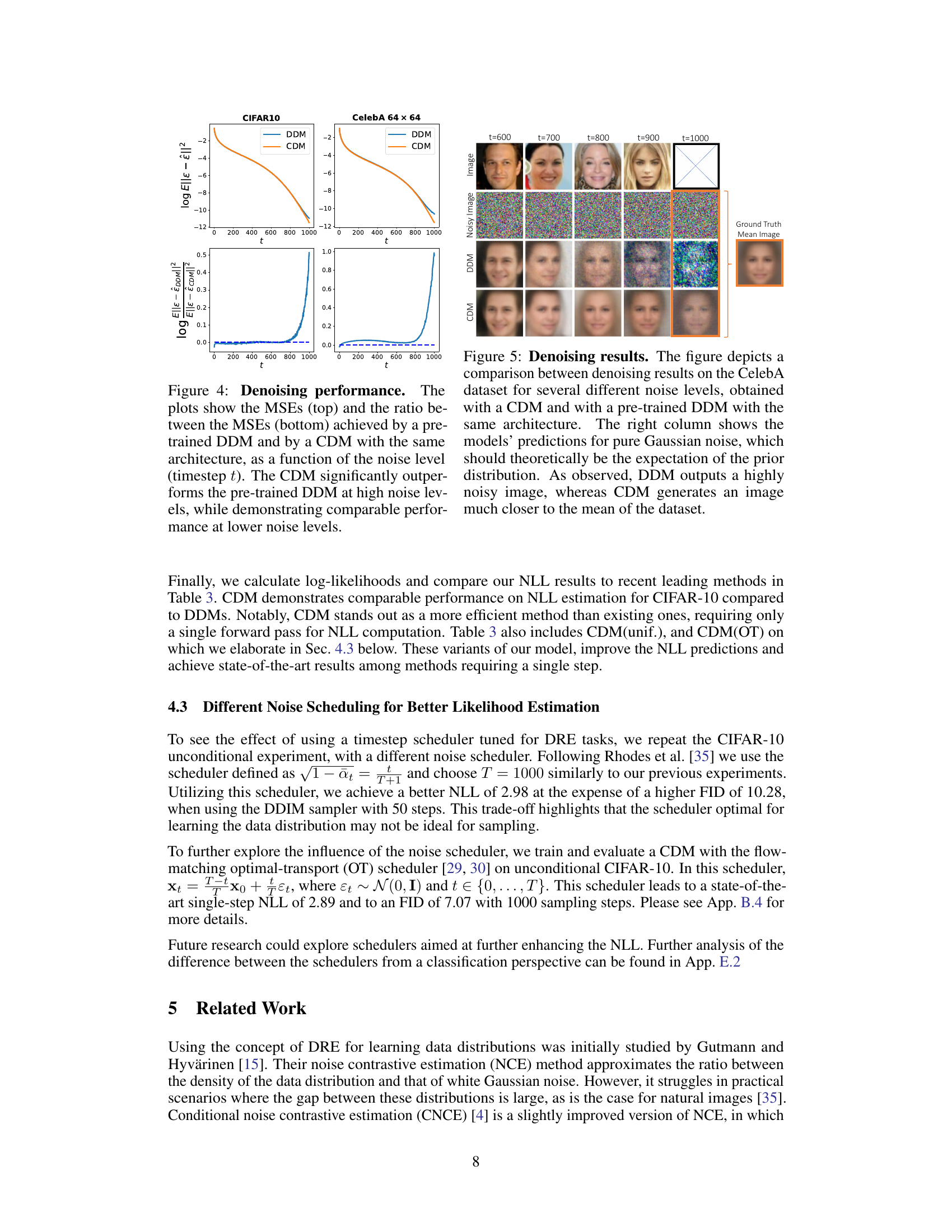
This figure compares the Mean Squared Error (MSE) of denoising between a pre-trained Denoising Diffusion Model (DDM) and a Classification Diffusion Model (CDM) across different noise levels represented by the timestep t. The top plots show the MSE for both models. The bottom plots display the ratio of the MSEs of the DDM to the CDM. The results demonstrate that the CDM achieves significantly lower MSE than the DDM at high noise levels, while showing comparable performance at lower noise levels. This indicates that the CDM is a more effective denoiser, particularly in scenarios with significant noise.

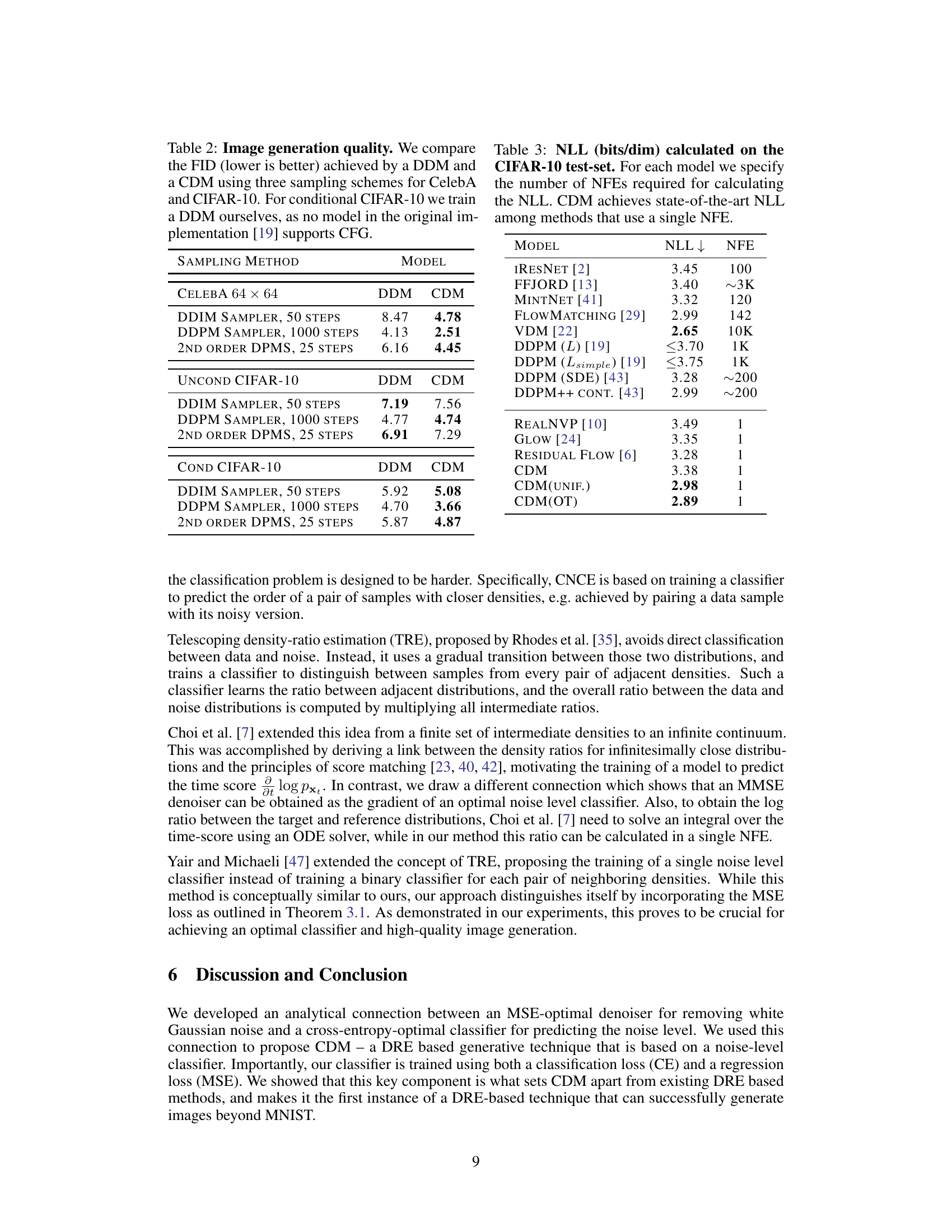
This figure compares the denoising performance of a Classification Diffusion Model (CDM) and a Denoising Diffusion Model (DDM) on the CelebA dataset. For several noise levels (represented by timesteps t=600, 700, 800, 900, 1000), the figure shows the original image, the noisy image, the DDM’s denoised image, and the CDM’s denoised image. The rightmost column shows the models’ attempts to denoise pure Gaussian noise; ideally, they should produce an image resembling the average of the dataset. The CDM outperforms the DDM, producing denoised images that are significantly closer to the original images, especially at higher noise levels, and its reconstruction from pure noise is also much closer to the mean image.

This figure compares image samples generated by Classification Diffusion Models (CDMs) and the state-of-the-art method for density ratio estimation (TRE). The left side shows high-quality image samples from CDMs trained on CelebA and CIFAR-10 datasets, demonstrating the ability of the new model to generate realistic images of complex objects. In contrast, the right side displays samples from TRE, showing its failure in capturing complex distributions, which highlights the significance of the CDM approach.

This figure compares image samples generated by Classification Diffusion Models (CDMs) and Telescoping Density Ratio Estimation (TRE). The left side shows high-quality images generated by CDMs trained on CelebA and CIFAR-10 datasets. The right side shows samples from TRE, a state-of-the-art DRE method, which struggles to generate comparable quality images, particularly on the more complex CIFAR-10 dataset. The figure highlights the success of CDMs in learning high-dimensional image distributions, a challenge that previous DRE methods have failed to overcome.

This figure compares the denoising capabilities of two models: one trained with cross-entropy (CE) loss only, and another trained with both CE and mean squared error (MSE) loss. The results show significantly better denoising performance for the model trained with both losses, especially at lower noise levels. This highlights the importance of incorporating MSE loss in the model training for accurate denoising.

This figure compares the log probability of noise level predicted by a classifier trained only with cross-entropy loss and a classifier trained with both cross-entropy and mean squared error loss. It shows that using only cross-entropy loss limits the accuracy of the classifier to the vicinity of the true label, while adding MSE loss allows the classifier to achieve accurate predictions globally, which is essential for obtaining accurate log likelihood estimation. The SoftMax function is used for probability normalization in the figure.

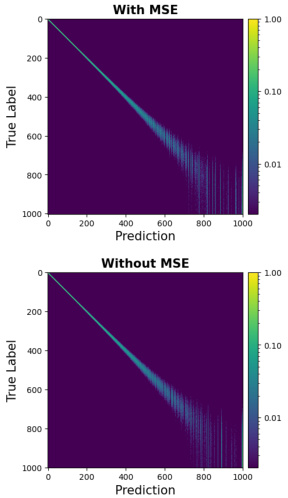
The figure compares the log probability of a noise-level classifier trained using only cross-entropy (CE) loss against one trained with both CE and mean squared error (MSE) loss. It shows that using only CE loss restricts accurate predictions to the vicinity of the correct label. Incorporating MSE loss allows for globally accurate predictions, demonstrating the importance of MSE for optimal classifier training in the context of density ratio estimation.

More on tables

This table compares the performance of a classification diffusion model (CDM) trained with different loss functions: cross-entropy (CE) only, mean squared error (MSE) only, and both CE and MSE. The results show that using both CE and MSE leads to significantly better classification accuracy, lower MSE, lower FID, and most importantly, much lower NLL (negative log-likelihood). The table highlights the importance of including the MSE loss for achieving an optimal classifier, which is crucial for accurate likelihood estimation, a key advantage of the proposed CDM approach.

This table compares the FID scores of CDMs and DDM models on CelebA and CIFAR-10 datasets using three different sampling methods: DDIM sampler (50 steps), DDPM sampler (1000 steps), and 2nd order DPMS (25 steps). Lower FID scores indicate better image generation quality. A separate comparison is shown for unconditional and conditional CIFAR-10 generation, highlighting the performance in both scenarios.

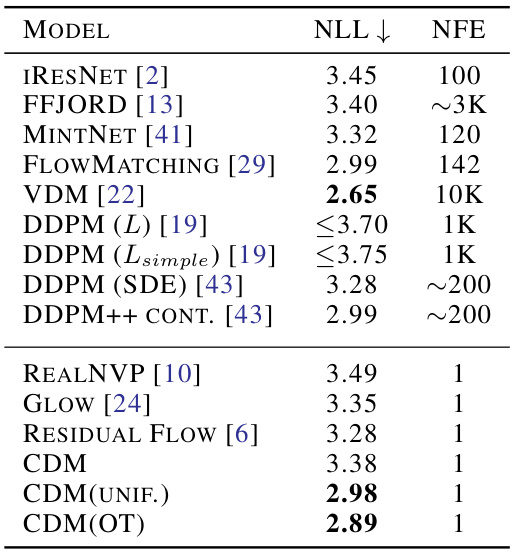
This table presents a comparison of the negative log-likelihood (NLL) achieved by various generative models on the CIFAR-10 dataset. The NLL measures how well a model estimates the probability density of the data. Lower NLL indicates better performance. The table also specifies the number of neural function evaluations (NFEs) needed to compute the NLL for each method. A key finding is that the proposed Classification Diffusion Model (CDM), along with its variants CDM(UNIF.) and CDM(OT), achieves state-of-the-art NLL among methods requiring only a single NFE. This demonstrates the efficiency and effectiveness of the CDM in likelihood estimation.

This table compares the performance of a classifier trained using only cross-entropy loss (CE), only mean squared error loss (MSE), and both CE and MSE. It highlights that using both losses is crucial for achieving high classification accuracy, low CE and MSE, and good FID (Fréchet Inception Distance) and NLL (negative log-likelihood) scores. The results demonstrate that only using CE or MSE leads to suboptimal performance.

Full paper

#