TL;DR#
Many existing neural combinatorial optimization (NCO) solvers struggle with large-scale problems, often relying on problem-specific heuristics or employing separate training schemes for dividing and conquering stages. These limitations hinder the general applicability of existing methods and often lead to suboptimal solutions.
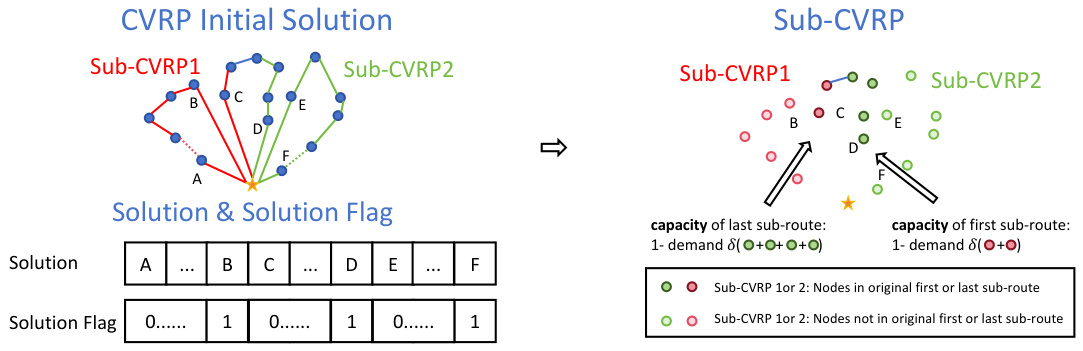
To overcome these challenges, this paper introduces a unified neural divide-and-conquer framework (UDC). This framework uses a high-efficiency Graph Neural Network (GNN) for instance division and a fixed-length sub-path solver for conquering sub-problems. Crucially, UDC employs a novel Divide-Conquer-Reunion (DCR) training method to address the negative impacts of sub-optimal division policies. The results show that UDC significantly outperforms existing methods across various large-scale combinatorial optimization problems.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a unified framework (UDC) for large-scale combinatorial optimization problems. This addresses the limitations of existing methods that rely on problem-specific heuristics or separate training schemes. The UDC framework’s superior performance and extensive applicability across diverse CO problems makes it a significant contribution to the field, opening up new avenues for research and practical applications. The paper also introduces a novel RL-based training method (DCR) that significantly improves the effectiveness of neural divide-and-conquer methods, offering a valuable new tool for researchers.
Visual Insights#

🔼 This figure illustrates the workflow of the Unified Neural Divide-and-Conquer (UDC) framework for three different large-scale combinatorial optimization problems: Vehicle Routing Problem (VRP), 0-1 Knapsack Problem (KP), and Maximum Independent Set (MIS). It shows the two main stages of the UDC framework: the dividing stage and the conquering stage. The dividing stage uses an Anisotropic Graph Neural Network (AGNN) to generate an initial solution and then divide the problem into subproblems. The conquering stage then uses problem-specific solvers to solve each subproblem. The subproblem solutions are then combined to form the final solution. The figure highlights the different steps involved in the process and the different types of networks and solvers used for each problem.
read the caption
Figure 1: The solving process of the proposed UDC on large-scale VRP, 0-1 Knapsack Problem (KP), and Maximum Independent Set (MIS).

🔼 This table compares the proposed UDC framework with other existing neural divide-and-conquer methods. It highlights key differences in the dividing and conquering policies used (neural vs. heuristic), whether the impact of sub-optimal dividing policies was considered during training, and whether a unified or separate training scheme was employed. The table demonstrates that UDC is unique in its use of learning-based policies for both stages and its unified training approach, which addresses the negative impact of sub-optimal dividing policies.
read the caption
Table 1: Comparison between our UDC and the other existing neural divide-and-conquer methods. The proposed UDC utilizes learning-based policies in both the dividing and conquering stages. Moreover, UDC is the first to achieve a superior unified training scheme by considering the negative impact of sub-optimal dividing policies on solution generation.
In-depth insights#
Unified NCO#
A unified neural combinatorial optimization (NCO) framework signifies a paradigm shift in tackling complex combinatorial problems. Instead of employing separate models for dividing and conquering subproblems, a unified approach integrates these stages seamlessly. This eliminates the performance bottlenecks often observed in two-stage methods stemming from suboptimal dividing policies and the lack of inter-stage coordination. A unified architecture allows for end-to-end training, optimizing both division and solution strategies concurrently. This, in turn, facilitates superior generalization and adaptability to diverse large-scale problems. While single-stage NCO solvers have shown promise on smaller instances, their performance degrades significantly with increasing scale. A unified framework addresses this scalability issue by leveraging the efficiency of divide-and-conquer strategies within a unified neural network, leading to a more robust and effective solution, particularly for large-scale problems. The key advantage lies in leveraging the benefits of both single-stage and two-stage approaches to achieve superior performance and scalability, exceeding the capabilities of either method alone.
DCR Training#
The Divide-Conquer-Reunion (DCR) training method is a novel approach designed to address the limitations of existing neural divide-and-conquer methods for combinatorial optimization. Existing methods often suffer from suboptimal dividing policies, negatively impacting solution quality. DCR mitigates this by introducing a reunion step after the conquer stage, enabling the correction of errors from initial sub-problem divisions. This unified training scheme, unlike separate training, considers the interdependencies between dividing and conquering stages, leading to more robust and accurate solutions. The process involves iteratively refining sub-solutions, resulting in improved overall solution quality. The use of a fixed-length sub-path solver in the conquer stage contributes to efficiency, allowing for parallel processing of subproblems and making DCR applicable to general CO problems. This approach is innovative because it directly addresses the problem of suboptimality within a unified framework, demonstrating the potential to improve solutions for large scale CO problems.
General CO#
A hypothetical research paper section titled ‘General CO’ would likely explore the applicability of developed methods to a wide range of combinatorial optimization problems. This would move beyond specific problem types (like TSP or CVRP) to assess performance on diverse, less-structured problems. The key challenge is generalizability: can the proposed framework solve problems not explicitly considered during training? The authors might demonstrate this through experimental results across different problem classes, analyzing how problem characteristics impact performance. This would involve carefully selected benchmark problems representing a spectrum of difficulty and structure, showing consistent, near-optimal solutions. Scalability would also be a crucial factor, demonstrating the approach can handle increasingly large problem instances efficiently. Crucially, a lack of problem-specific heuristics or pre-training would be a significant finding, illustrating the method’s adaptability. The discussion would likely contrast this ‘general’ approach with existing methods that rely heavily on problem-specific designs or extensive pre-training, emphasizing the advantages of a more universal technique.
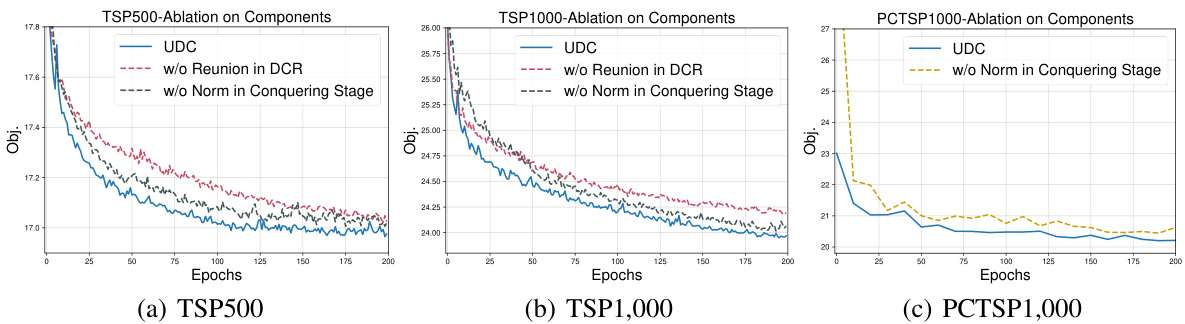
Ablation Studies#
Ablation studies systematically remove components of a model or system to assess their individual contributions. In a research paper, this section would provide valuable insights into the model’s design choices. For example, removing a specific neural network layer reveals its impact on overall performance. By carefully observing the effects of removing each component, researchers can quantify the importance of each part, and identify potential redundancies or inefficiencies. Well-designed ablation studies should consider various aspects of the model. These could include: network architectures, training methodologies (e.g., comparing different optimizers or loss functions), and data processing techniques. The results will help to establish the model’s robustness and highlight areas for improvement. The strength of an ablation study is its ability to provide a clear, quantitative evaluation of a model’s building blocks, leading to more informed design decisions and a deeper understanding of the model’s inner workings.
Future Work#
The authors mention exploring better loss functions to enhance training efficiency and extend the framework’s applicability to other CO problems. Improving loss functions is a crucial next step, as it directly affects the model’s ability to learn and generalize effectively. This suggests a need for more sophisticated reward shaping and potentially a deeper exploration of different RL algorithms beyond REINFORCE. Expanding to more problem types will require careful consideration of problem-specific constraints and the development of suitable, adaptable sub-problem solvers. Addressing challenges with large-scale generalization, especially in TSP, is another key point. The observation that sub-optimal dividing policies negatively impact large instances suggests exploring alternative dividing strategies that are more robust to scale. Investigating heuristic-based hybrid approaches could also prove valuable for handling the complexity of large-scale instances. Overall, the future work plan highlights the need for methodological refinement and broader applicability, indicating a clear path towards a more robust and generally applicable framework.
More visual insights#
More on figures

🔼 This figure shows the training curves for three different training schemes for UDC: Unified Training (UDC), Pre-train + Joint Training, and Pre-train + Train Dividing. The unified training scheme shows significantly better convergence and lower objective function values compared to the other two schemes, especially on larger instances (TSP1000). This highlights the benefits of the UDC framework’s unified training approach in achieving better performance compared to the separate training approaches used in other existing neural divide-and-conquer methods.
read the caption
Figure 3: Training curves of UDC variants with different training schemes.
🔼 This figure illustrates the overall framework of the UDC model in solving three different large-scale combinatorial optimization problems: Vehicle Routing Problem (VRP), 0-1 Knapsack Problem (KP), and Maximum Independent Set (MIS). The dividing stage utilizes an Anisotropic Graph Neural Network (AGNN) to generate an initial solution, which is then used to decompose the problem into subproblems in the conquering stage. The conquering stage employs appropriate constructive neural solvers (such as AGNN for MIS problems) to solve each subproblem. Finally, the solutions from each subproblem are merged to obtain a final solution to the original large-scale problem. The figure highlights the different components of the UDC framework and how they interact to solve different types of combinatorial optimization problems. It showcases the versatility of the UDC framework, which doesn’t rely on problem-specific heuristics.
read the caption
Figure 1: The solving process of the proposed UDC on large-scale VRP, 0-1 Knapsack Problem (KP), and Maximum Independent Set (MIS).
🔼 This figure illustrates the overall process of the proposed Unified Neural Divide-and-Conquer (UDC) framework for solving three different large-scale combinatorial optimization problems: Vehicle Routing Problem (VRP), 0-1 Knapsack Problem (KP), and Maximum Independent Set (MIS). The figure shows the two-stage process (dividing and conquering) and the sub-problem preparation steps that are involved in each problem. It highlights that UDC uses a heatmap-based solver with an Anisotropic Graph Neural Network (AGNN) for the dividing stage and problem-specific constructive neural solvers for the conquering stage. The figure also shows how the sub-problems are prepared for each problem, taking into account the specific constraints and characteristics of each problem. The use of a unified training scheme is implied by the figure’s depiction of the overall process.
read the caption
Figure 1: The solving process of the proposed UDC on large-scale VRP, 0-1 Knapsack Problem (KP), and Maximum Independent Set (MIS).
🔼 This figure illustrates the overall pipeline of the UDC framework for solving three different large-scale combinatorial optimization problems: Vehicle Routing Problem (VRP), 0-1 Knapsack Problem (KP), and Maximum Independent Set (MIS). Each problem is shown with its respective stages: dividing stage and conquering stage. The dividing stage uses an Anisotropic Graph Neural Network (AGNN) to generate an initial solution, which informs the decomposition of the original problem into smaller subproblems. The conquering stage then solves these subproblems using appropriate solvers (e.g., VRP solver, KP solver, MIS solver) before merging the results to obtain a final solution. The figure also highlights the use of a heatmap to represent the instance, the preparation of the subproblems to integrate problem-specific constraints, and the merging of subproblem solutions. It visually demonstrates how the unified divide-and-conquer approach works across different problem types.
read the caption
Figure 1: The solving process of the proposed UDC on large-scale VRP, 0-1 Knapsack Problem (KP), and Maximum Independent Set (MIS).

🔼 This figure illustrates the workflow of the Unified Neural Divide-and-Conquer (UDC) framework for three different large-scale combinatorial optimization problems: Vehicle Routing Problem (VRP), 0-1 Knapsack Problem (KP), and Maximum Independent Set (MIS). It shows how UDC utilizes a two-stage process: a dividing stage that employs an Anisotropic Graph Neural Network (AGNN) to decompose the problem into smaller, manageable subproblems, and a conquering stage that uses specialized solvers (e.g., AGNN for MIS, POMO or ICAM for VRPs) to solve these subproblems. The subproblem solutions are then merged to produce a final solution for the original large-scale problem. The figure provides a visual representation of the data flow and processing steps involved in each stage for each of the three problem types.
read the caption
Figure 1: The solving process of the proposed UDC on large-scale VRP, 0-1 Knapsack Problem (KP), and Maximum Independent Set (MIS).

🔼 This figure illustrates the workflow of the UDC framework for solving three different large-scale combinatorial optimization problems: Vehicle Routing Problem (VRP), 0-1 Knapsack Problem (KP), and Maximum Independent Set (MIS). It shows how the UDC method, which is a two-stage approach, processes each problem. The first stage is the dividing stage, where the instance is divided into subproblems using an Anisotropic Graph Neural Network (AGNN). The second stage is the conquering stage, where each subproblem is solved using a suitable constructive neural solver (e.g., AGNN for MIS, POMO for VRPs, etc.). Finally, the solutions of the subproblems are merged to get the final solution for the original problem. The figure highlights the different steps involved in the process for each of the three problems, including sub-problem preparation, and emphasizes the overall architecture of UDC.
read the caption
Figure 1: The solving process of the proposed UDC on large-scale VRP, 0-1 Knapsack Problem (KP), and Maximum Independent Set (MIS).

🔼 This figure illustrates the workflow of the UDC framework applied to three different large-scale combinatorial optimization problems: Vehicle Routing Problem (VRP), 0-1 Knapsack Problem (KP), and Maximum Independent Set (MIS). It shows how the UDC’s two-stage approach, dividing and conquering, works in practice. The dividing stage uses an Anisotropic Graph Neural Network (AGNN) to decompose the problem into smaller subproblems. The conquering stage then employs problem-specific solvers to find solutions for these subproblems. Finally, these sub-solutions are combined to produce the final solution. The figure highlights the differences in the subproblem generation and solution processes for the three problem types, emphasizing the framework’s versatility and adaptability to various combinatorial optimization tasks. Different colors and shapes represent various components of the solution process and sub-problems in the figure.
read the caption
Figure 1: The solving process of the proposed UDC on large-scale VRP, 0-1 Knapsack Problem (KP), and Maximum Independent Set (MIS).

🔼 This figure illustrates the workflow of the Unified Neural Divide-and-Conquer (UDC) framework for solving three different large-scale combinatorial optimization problems: Vehicle Routing Problem (VRP), 0-1 Knapsack Problem (KP), and Maximum Independent Set (MIS). It shows the two main stages of UDC: the dividing stage and the conquering stage. The dividing stage uses an Anisotropic Graph Neural Network (AGNN) to decompose the original problem into smaller subproblems. The conquering stage employs appropriate solvers for each subproblem (AGNN for MIS, POMO or ICAM for VRPs, and a specific solver for KP). The figure highlights the input, intermediate steps, and output for each problem, illustrating the iterative refinement of solutions through subproblem solving and merging.
read the caption
Figure 1: The solving process of the proposed UDC on large-scale VRP, 0-1 Knapsack Problem (KP), and Maximum Independent Set (MIS).

🔼 This figure illustrates the workflow of the proposed UDC framework for three different large-scale combinatorial optimization problems: Vehicle Routing Problem (VRP), 0-1 Knapsack Problem (KP), and Maximum Independent Set (MIS). It shows the two main stages of the UDC approach: the dividing stage and the conquering stage. In the dividing stage, a heatmap-based method with an Anisotropic Graph Neural Network (AGNN) is used to generate an initial solution and divide the problem into subproblems. The conquering stage then employs problem-specific constructive neural solvers (e.g., AGNN for MIS, POMO for VRPs) to solve the subproblems. The subproblem solutions are then merged to form a final solution for the original problem. The figure highlights the different steps involved for each problem type and the interdependencies between the stages, such as how the initial solution from the dividing stage influences the subsequent subproblem generation in the conquering stage.
read the caption
Figure 1: The solving process of the proposed UDC on large-scale VRP, 0-1 Knapsack Problem (KP), and Maximum Independent Set (MIS).

🔼 This figure illustrates the workflow of the UDC framework across three different large-scale combinatorial optimization problems: Vehicle Routing Problem (VRP), 0-1 Knapsack Problem (KP), and Maximum Independent Set (MIS). It shows how UDC’s two-stage process (dividing and conquering) operates. The dividing stage uses an Anisotropic Graph Neural Network (AGNN) to decompose the original problem into subproblems, visualized by different colored sections of the graph. The conquering stage uses specialized solvers for each type of subproblem (VRP solver, KP solver, MIS solver) to find solutions for the subproblems. Finally, the subproblem solutions are merged to obtain a solution for the original problem. The figure highlights the key components of UDC, including the AGNN for dividing, the specialized solvers for conquering, and the final merging step.
read the caption
Figure 1: The solving process of the proposed UDC on large-scale VRP, 0-1 Knapsack Problem (KP), and Maximum Independent Set (MIS).

🔼 This figure illustrates the workflow of the UDC framework for three different large-scale combinatorial optimization problems: Vehicle Routing Problem (VRP), 0-1 Knapsack Problem (KP), and Maximum Independent Set (MIS). It shows how UDC uses a two-stage process: a dividing stage using an Anisotropic Graph Neural Network (AGNN) to decompose the problem into subproblems, and a conquering stage employing problem-specific solvers (AGNN for MIS, POMO or ICAM for VRPs) to solve the subproblems. The subproblems are then merged into a final solution, and the process iterates with refinement. Different visual elements are used to highlight the data representation and transformation at each stage.
read the caption
Figure 1: The solving process of the proposed UDC on large-scale VRP, 0-1 Knapsack Problem (KP), and Maximum Independent Set (MIS).

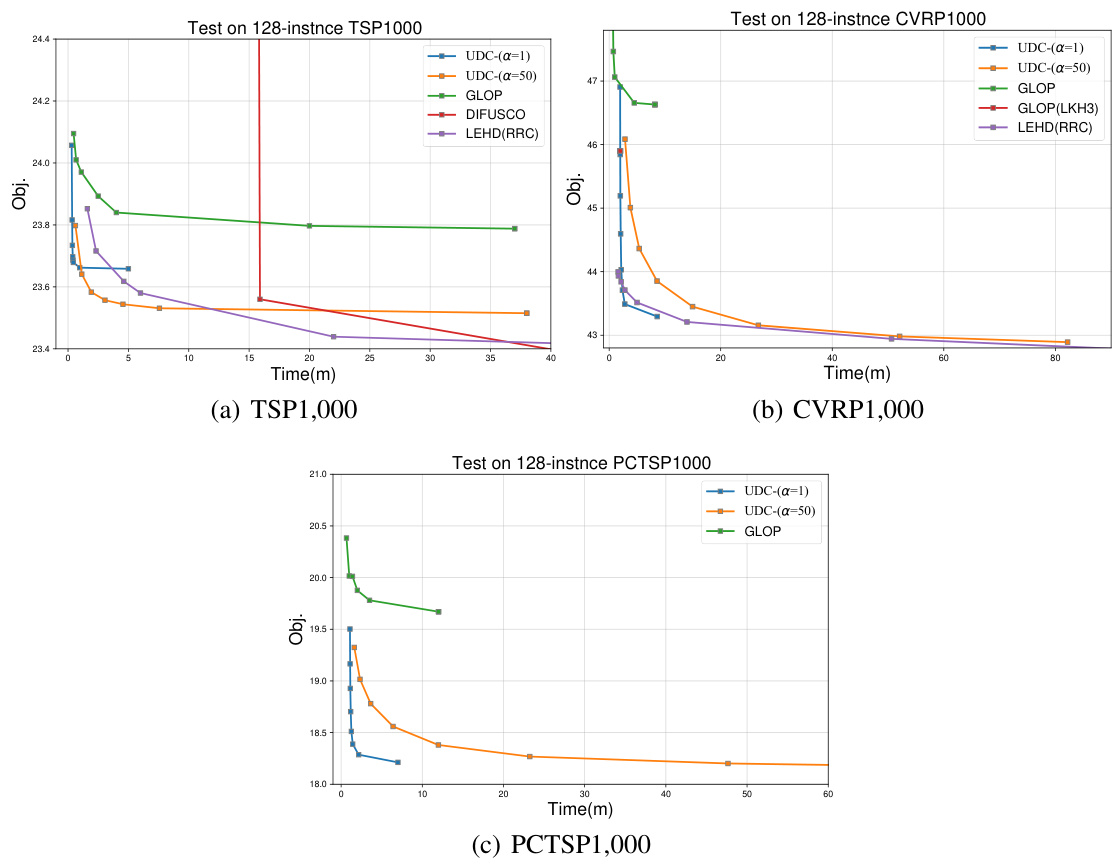
🔼 This figure visualizes the TSP solutions obtained by different methods on a random TSP instance. It shows the initial solution generated by the dividing stage of the UDC framework, the solutions after one and multiple rounds of conquering stages, and the optimal solution. The colors in the initial solution and the first conquering stage subfigures represent the different subproblems generated by the dividing policy. The objective function (Obj.) values are provided for each solution, and the figure illustrates how UDC progressively refines its solution toward the optimal one by solving subproblems.
read the caption
Figure 7: Visualization of TSP solutions on a random TSP instance, Obj. represents the objective function. The colors in subfigure (a)(b) represent sub-problems.
More on tables

🔼 This table compares the proposed UDC framework with other existing neural divide-and-conquer methods. It highlights key differences in dividing and conquering policies, how these methods handle the negative impact of suboptimal dividing policies, and whether they utilize unified or separate training schemes. The table demonstrates that UDC is unique in its use of learning-based policies in both stages and its unified training scheme which addresses the negative impacts of sub-optimal dividing policies, resulting in a superior solution generation approach.
read the caption
Table 1: Comparison between our UDC and the other existing neural divide-and-conquer methods. The proposed UDC utilizes learning-based policies in both the dividing and conquering stages. Moreover, UDC is the first to achieve a superior unified training scheme by considering the negative impact of sub-optimal dividing policies on solution generation.
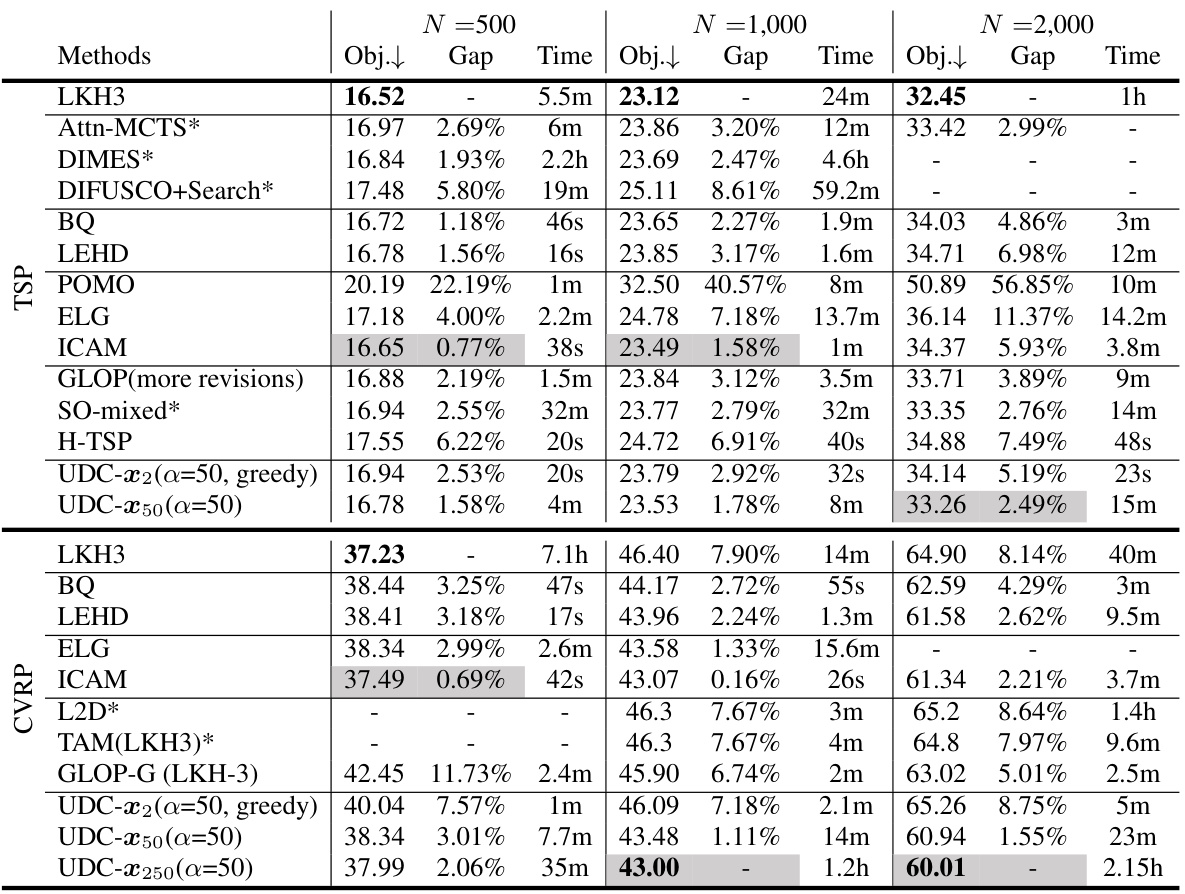
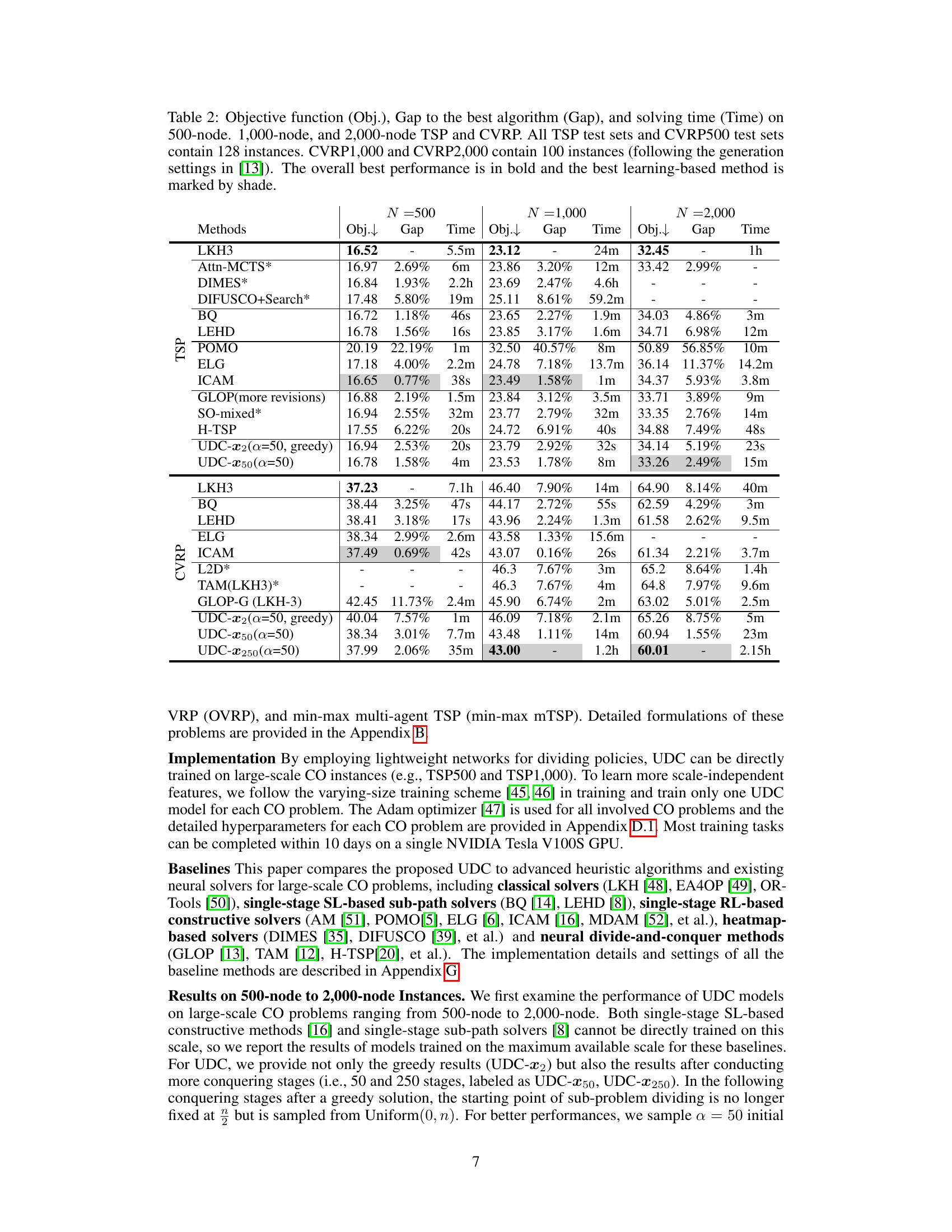
🔼 This table compares the performance of various methods on solving TSP and CVRP problems of different sizes (500, 1000, and 2000 nodes). It shows the objective function value (Obj.), the gap between the method’s result and the best known result (Gap), and the time taken to solve each instance (Time). The best overall performance for each problem size is highlighted in bold, and the best performing learning-based method is shaded.
read the caption
Table 2: Objective function (Obj.), Gap to the best algorithm (Gap), and solving time (Time) on 500-node, 1,000-node, and 2,000-node TSP and CVRP. All TSP test sets and CVRP500 test sets contain 128 instances. CVRP1,000 and CVRP2,000 contain 100 instances (following the generation settings in [13]). The overall best performance is in bold and the best learning-based method is marked by shade.

🔼 This table presents a comparison of the objective function values, gaps to the best-performing algorithm, and solution times for various methods on TSP and CVRP problems with 500, 1000, and 2000 nodes. The best overall performance for each problem size is highlighted in bold, and the best-performing learning-based method is shaded.
read the caption
Table 2: Objective function (Obj.), Gap to the best algorithm (Gap), and solving time (Time) on 500-node, 1,000-node, and 2,000-node TSP and CVRP. All TSP test sets and CVRP500 test sets contain 128 instances. CVRP1,000 and CVRP2,000 contain 100 instances (following the generation settings in [13]). The overall best performance is in bold and the best learning-based method is marked by shade.

🔼 This table compares the proposed UDC framework with other existing neural divide-and-conquer methods. It highlights key differences in their dividing and conquering policies, whether they consider the impact of sub-optimal dividing policies, and if they utilize a unified or separate training scheme. The table demonstrates that UDC is unique in its unified training approach and its consideration of sub-optimal dividing policies’ effects.
read the caption
Table 1: Comparison between our UDC and the other existing neural divide-and-conquer methods. The proposed UDC utilizes learning-based policies in both the dividing and conquering stages. Moreover, UDC is the first to achieve a superior unified training scheme by considering the negative impact of sub-optimal dividing policies on solution generation.
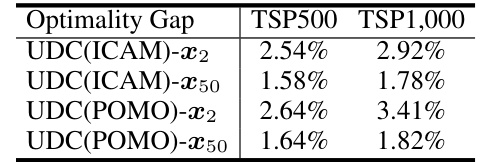
🔼 This table compares the proposed UDC framework with other existing neural divide-and-conquer methods. It highlights key differences in the dividing and conquering policies used (whether neural or heuristic), how these methods handle the negative impact of sub-optimal dividing policies, and whether they use a unified or separate training scheme for the two policies. The table demonstrates that UDC is unique in its use of learning-based policies in both stages and its unified training approach.
read the caption
Table 1: Comparison between our UDC and the other existing neural divide-and-conquer methods. The proposed UDC utilizes learning-based policies in both the dividing and conquering stages. Moreover, UDC is the first to achieve a superior unified training scheme by considering the negative impact of sub-optimal dividing policies on solution generation.

🔼 This table compares the proposed UDC framework with other existing neural divide-and-conquer methods. It highlights key differences in dividing and conquering policies (neural vs heuristic), whether the methods consider the impact of sub-optimal dividing policies, and whether the training of the two policies is unified or separate. The table shows that UDC is unique in its use of learning-based policies for both stages and its unified training scheme that addresses the negative effects of suboptimal dividing.
read the caption
Table 1: Comparison between our UDC and the other existing neural divide-and-conquer methods. The proposed UDC utilizes learning-based policies in both the dividing and conquering stages. Moreover, UDC is the first to achieve a superior unified training scheme by considering the negative impact of sub-optimal dividing policies on solution generation.
🔼 This table compares the proposed UDC framework with other existing neural divide-and-conquer methods. It highlights key differences in the dividing and conquering policies used (neural network-based or heuristic), whether the methods account for the negative impact of suboptimal dividing policies, and whether the training process is unified or separate. The table shows that UDC uniquely utilizes learning-based policies in both stages and employs a unified training scheme, addressing limitations of prior methods.
read the caption
Table 1: Comparison between our UDC and the other existing neural divide-and-conquer methods. The proposed UDC utilizes learning-based policies in both the dividing and conquering stages. Moreover, UDC is the first to achieve a superior unified training scheme by considering the negative impact of sub-optimal dividing policies on solution generation.

🔼 This table presents a comparison of different methods for solving Traveling Salesperson Problem (TSP) and Capacitated Vehicle Routing Problem (CVRP) instances of varying sizes (500, 1000, and 2000 nodes). The table shows the objective function value (Obj.), the gap between the obtained solution and the best-known solution (Gap), and the time taken to find the solution (Time). The best-performing method overall and the best-performing learning-based method for each problem size are highlighted.
read the caption
Table 2: Objective function (Obj.), Gap to the best algorithm (Gap), and solving time (Time) on 500-node, 1,000-node, and 2,000-node TSP and CVRP. All TSP test sets and CVRP500 test sets contain 128 instances. CVRP1,000 and CVRP2,000 contain 100 instances (following the generation settings in [13]). The overall best performance is in bold and the best learning-based method is marked by shade.
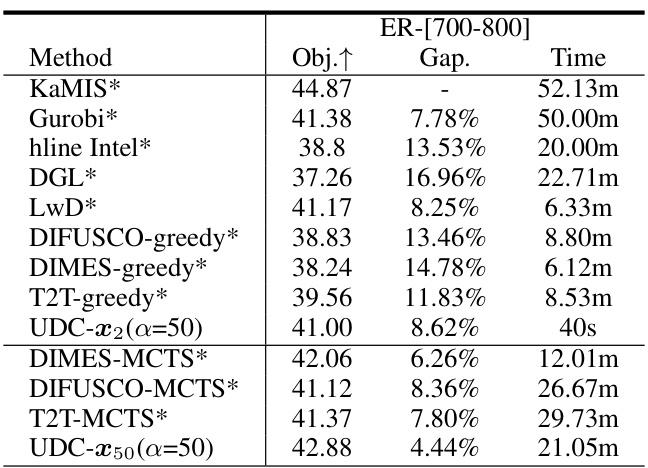
🔼 This table presents a comparison of the objective function values, gaps to the best-performing algorithm, and solving times for various methods on TSP and CVRP problems with 500, 1000, and 2000 nodes. The best overall performance for each problem size is highlighted in bold, and the best-performing learning-based method is shaded. The table provides a quantitative assessment of the different methods’ performance on large-scale combinatorial optimization problems.
read the caption
Table 2: Objective function (Obj.), Gap to the best algorithm (Gap), and solving time (Time) on 500-node, 1,000-node, and 2,000-node TSP and CVRP. All TSP test sets and CVRP500 test sets contain 128 instances. CVRP1,000 and CVRP2,000 contain 100 instances (following the generation settings in [13]). The overall best performance is in bold and the best learning-based method is marked by shade.

🔼 This table compares the proposed UDC framework with other existing neural divide-and-conquer methods. It highlights key differences in their dividing and conquering policies (whether neural or heuristic-based), how they handle the impact of sub-optimal dividing policies (ignored or considered), and whether they use a unified or separate training scheme for the two policies. The table shows that UDC uniquely utilizes learning-based policies in both stages and employs a unified training scheme, addressing limitations of previous methods.
read the caption
Table 1: Comparison between our UDC and the other existing neural divide-and-conquer methods. The proposed UDC utilizes learning-based policies in both the dividing and conquering stages. Moreover, UDC is the first to achieve a superior unified training scheme by considering the negative impact of sub-optimal dividing policies on solution generation.

🔼 This table presents a comparison of the objective function values, gaps to the best-performing algorithm, and solving times for different methods on TSP and CVRP problems with varying numbers of nodes (500, 1000, and 2000). The best overall performance for each metric is highlighted in bold, and the best-performing learning-based method is shaded. The number of instances used in the testing is also provided.
read the caption
Table 2: Objective function (Obj.), Gap to the best algorithm (Gap), and solving time (Time) on 500-node, 1,000-node, and 2,000-node TSP and CVRP. All TSP test sets and CVRP500 test sets contain 128 instances. CVRP1,000 and CVRP2,000 contain 100 instances (following the generation settings in [13]). The overall best performance is in bold and the best learning-based method is marked by shade.

🔼 This table presents a comparison of different methods for solving TSP and CVRP problems with varying instance sizes (500, 1000, and 2000 nodes). It shows the objective function value, the gap to the best-performing algorithm, and the solution time for each method. The best overall performance and the best learning-based methods are highlighted.
read the caption
Table 2: Objective function (Obj.), Gap to the best algorithm (Gap), and solving time (Time) on 500-node, 1,000-node, and 2,000-node TSP and CVRP. All TSP test sets and CVRP500 test sets contain 128 instances. CVRP1,000 and CVRP2,000 contain 100 instances (following the generation settings in [13]). The overall best performance is in bold and the best learning-based method is marked by shade.
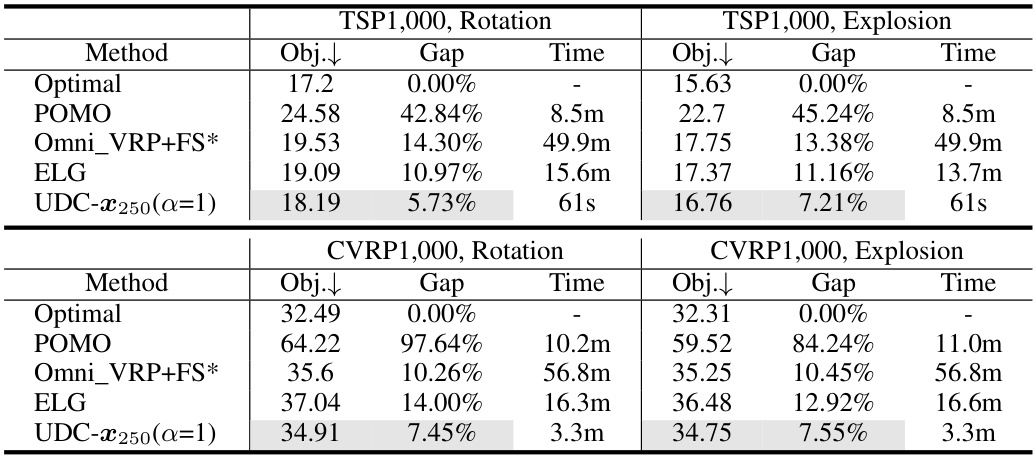
🔼 This table presents a comparison of different methods for solving TSP and CVRP problems of varying sizes (500, 1000, and 2000 nodes). The metrics used for comparison include the objective function value (Obj.), the gap between the method’s solution and the best-known solution (Gap), and the time taken to find the solution (Time). The best overall performance and the best among learning-based methods are highlighted.
read the caption
Table 2: Objective function (Obj.), Gap to the best algorithm (Gap), and solving time (Time) on 500-node, 1,000-node, and 2,000-node TSP and CVRP. All TSP test sets and CVRP500 test sets contain 128 instances. CVRP1,000 and CVRP2,000 contain 100 instances (following the generation settings in [13]). The overall best performance is in bold and the best learning-based method is marked by shade.

🔼 This table presents a comparison of the objective function values, gaps to the best-performing algorithm, and solving times for various neural combinatorial optimization methods on TSP and CVRP problems with 500, 1000, and 2000 nodes. The best overall performance for each metric is highlighted in bold, and the best-performing learning-based method is shaded. The table provides a quantitative assessment of the performance of different algorithms on increasingly larger problem sizes.
read the caption
Table 2: Objective function (Obj.), Gap to the best algorithm (Gap), and solving time (Time) on 500-node, 1,000-node, and 2,000-node TSP and CVRP. All TSP test sets and CVRP500 test sets contain 128 instances. CVRP1,000 and CVRP2,000 contain 100 instances (following the generation settings in [13]). The overall best performance is in bold and the best learning-based method is marked by shade.

🔼 This table presents a comparison of the objective function values, gaps to the best-performing algorithm, and solution times for different methods on TSP and CVRP problems with varying numbers of nodes (500, 1000, and 2000). The best overall performance for each metric is highlighted in bold, and the best-performing learning-based method is shaded.
read the caption
Table 2: Objective function (Obj.), Gap to the best algorithm (Gap), and solving time (Time) on 500-node, 1,000-node, and 2,000-node TSP and CVRP. All TSP test sets and CVRP500 test sets contain 128 instances. CVRP1,000 and CVRP2,000 contain 100 instances (following the generation settings in [13]). The overall best performance is in bold and the best learning-based method is marked by shade.

🔼 This table presents a comparison of the objective function values, gaps to the best-performing algorithm, and solving times for different methods on TSP and CVRP problems with 500, 1000, and 2000 nodes. The best overall performance for each problem size is highlighted in bold, and the best-performing learning-based method is shaded.
read the caption
Table 2: Objective function (Obj.), Gap to the best algorithm (Gap), and solving time (Time) on 500-node, 1,000-node, and 2,000-node TSP and CVRP. All TSP test sets and CVRP500 test sets contain 128 instances. CVRP1,000 and CVRP2,000 contain 100 instances (following the generation settings in [13]). The overall best performance is in bold and the best learning-based method is marked by shade.

🔼 This table presents a comparison of different methods for solving TSP and CVRP problems with varying sizes (500, 1000, and 2000 nodes). It shows the objective function values, the gap between each method’s solution and the optimal solution, and the time taken to find the solution. The best performing method for each problem size is highlighted in bold, and the best-performing learning-based method is shaded.
read the caption
Table 2: Objective function (Obj.), Gap to the best algorithm (Gap), and solving time (Time) on 500-node, 1,000-node, and 2,000-node TSP and CVRP. All TSP test sets and CVRP500 test sets contain 128 instances. CVRP1,000 and CVRP2,000 contain 100 instances (following the generation settings in [13]). The overall best performance is in bold and the best learning-based method is marked by shade.

🔼 This table presents a comparison of different methods for solving TSP and CVRP problems with varying instance sizes (500, 1000, and 2000 nodes). The results are shown in terms of objective function value, the gap to the best-performing algorithm, and the time taken to solve the problems. The best overall performance and the best learning-based method for each problem and size are highlighted.
read the caption
Table 2: Objective function (Obj.), Gap to the best algorithm (Gap), and solving time (Time) on 500-node, 1,000-node, and 2,000-node TSP and CVRP. All TSP test sets and CVRP500 test sets contain 128 instances. CVRP1,000 and CVRP2,000 contain 100 instances (following the generation settings in [13]). The overall best performance is in bold and the best learning-based method is marked by shade.

🔼 This table presents a comparison of the objective function values, gaps to the best algorithm, and solving times for different methods on TSP and CVRP problems with 500, 1000, and 2000 nodes. The best performing method for each problem size is highlighted in bold, and the best-performing learning-based method is shaded.
read the caption
Table 2: Objective function (Obj.), Gap to the best algorithm (Gap), and solving time (Time) on 500-node, 1,000-node, and 2,000-node TSP and CVRP. All TSP test sets and CVRP500 test sets contain 128 instances. CVRP1,000 and CVRP2,000 contain 100 instances (following the generation settings in [13]). The overall best performance is in bold and the best learning-based method is marked by shade.

🔼 This table compares the proposed UDC framework with other existing neural divide-and-conquer methods in terms of dividing and conquering policies, the consideration of the negative impact of suboptimal dividing policies, and the training schemes used for the two policies. It highlights that UDC is unique in using learning-based policies for both stages and employing a unified training scheme to address the suboptimality issue.
read the caption
Table 1: Comparison between our UDC and the other existing neural divide-and-conquer methods. The proposed UDC utilizes learning-based policies in both the dividing and conquering stages. Moreover, UDC is the first to achieve a superior unified training scheme by considering the negative impact of sub-optimal dividing policies on solution generation.

🔼 This table compares the proposed UDC framework with other existing neural divide-and-conquer methods. It highlights key differences in the dividing and conquering policies used (neural or heuristic-based), whether the impact of sub-optimal dividing policies was considered during training, and if the training was unified or separate for both policies. UDC is shown to be unique in its use of learning-based policies in both stages and its unified training scheme.
read the caption
Table 1: Comparison between our UDC and the other existing neural divide-and-conquer methods. The proposed UDC utilizes learning-based policies in both the dividing and conquering stages. Moreover, UDC is the first to achieve a superior unified training scheme by considering the negative impact of sub-optimal dividing policies on solution generation.

🔼 This table compares the proposed UDC framework with other existing neural divide-and-conquer methods. It highlights key differences in dividing and conquering policies (neural or heuristic-based), how sub-optimal dividing policies are handled (considered or ignored), and whether the training of these policies is unified or separate. The table shows that UDC is unique in its unified training approach and use of learning-based policies in both stages.
read the caption
Table 1: Comparison between our UDC and the other existing neural divide-and-conquer methods. The proposed UDC utilizes learning-based policies in both the dividing and conquering stages. Moreover, UDC is the first to achieve a superior unified training scheme by considering the negative impact of sub-optimal dividing policies on solution generation.
Full paper#