↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat
TL;DR#
Current radiance representations in 3D generative modeling struggle with either implicit feature decoders that limit model power or spatial unstructuredness that hinders integration with mainstream 3D diffusion methods. These limitations result in lower-quality models, and the use of many parameters makes training and inference inefficient. This paper addresses these issues.
The proposed solution, GaussianCube, uses a novel densification-constrained Gaussian fitting algorithm and optimal transport to create a structured, explicit representation. This structured approach allows for the use of standard 3D U-Net architectures in diffusion modeling. Furthermore, the high-accuracy fitting dramatically reduces the number of required parameters, leading to significantly improved speed and efficiency. Extensive experiments demonstrate state-of-the-art results across multiple 3D generative modeling tasks.
Key Takeaways#
Why does it matter?#
This paper is crucial because it introduces GaussianCube, a novel radiance representation that significantly advances 3D generative modeling. Its structured and explicit nature, combined with high-accuracy fitting using fewer parameters, overcomes limitations of existing methods, enabling efficient integration with mainstream 3D diffusion models. This opens exciting avenues for research in high-fidelity 3D object and avatar generation, as well as text-to-3D synthesis.
Visual Insights#

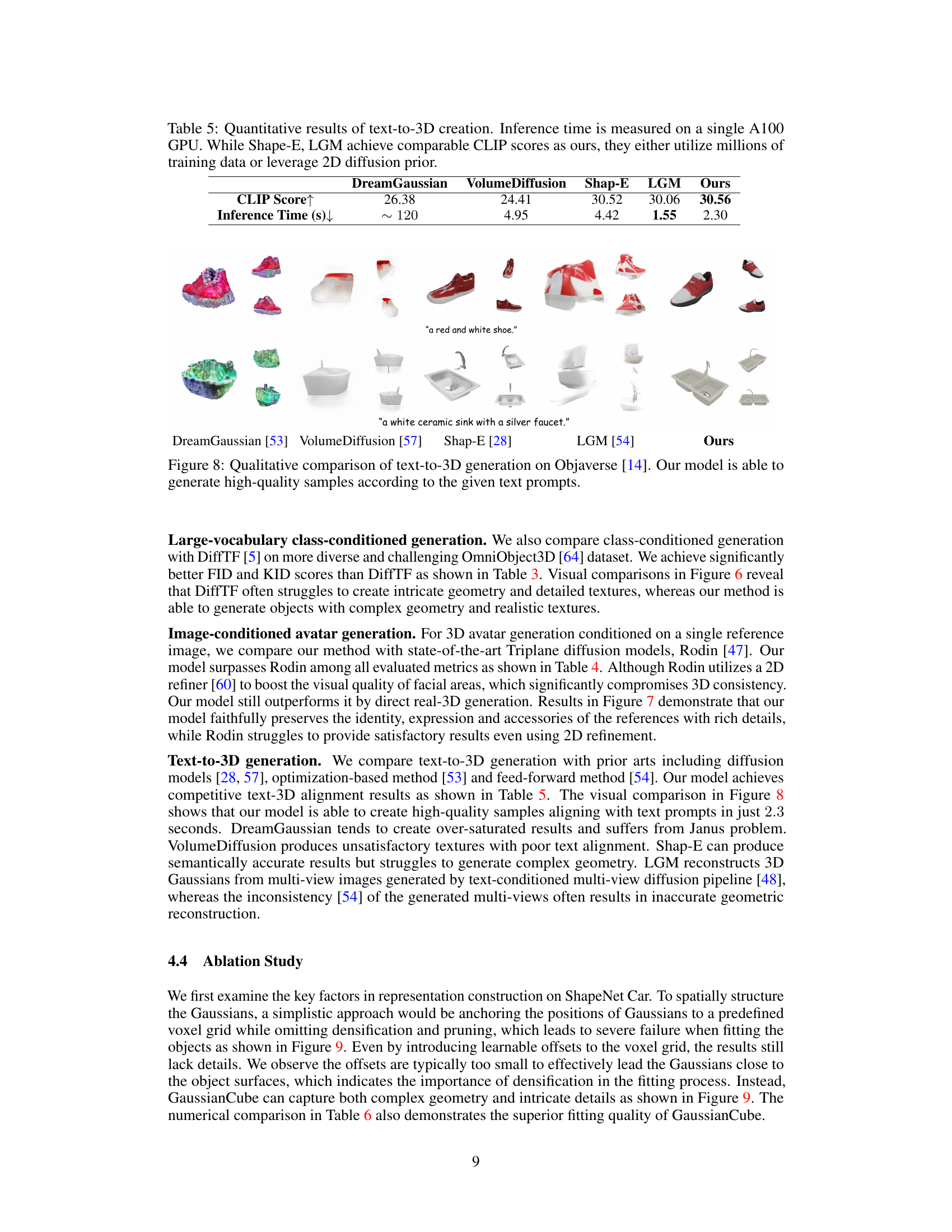
This figure showcases the model’s ability to generate various 3D objects and avatars. The top three rows demonstrate unconditional and class-conditional object generation, highlighting detailed textures and complex geometries. The fourth row shows image-conditioned digital avatar generation, demonstrating the model’s capacity to create realistic avatars from single portraits. The bottom row displays text-to-3D generation, illustrating how the model produces high-quality 3D models based on text descriptions.

This table compares several existing 3D representations against the proposed GaussianCube method. The comparison focuses on four key aspects: spatial structure (whether the representation is organized in a structured grid or is unstructured), explicitness (whether the representation is directly defined or requires an implicit feature decoder), real-time rendering capability, and the relative number of parameters required to achieve comparable quality. GaussianCube excels in all aspects except for the number of parameters, which is significantly lower (1.0x) than existing methods.
In-depth insights#
GaussianCube: Fitting#
The core of GaussianCube lies in its novel fitting procedure. Instead of directly using the Gaussian Splatting algorithm’s adaptive density, GaussianCube employs a densification-constrained approach. This ensures a fixed number of Gaussians regardless of the object complexity, paving the way for efficient structured representation. The constraint is cleverly implemented by controlling the densification process, balancing the addition of new Gaussians with the removal of less-significant ones. This innovative strategy cleverly addresses the challenge of maintaining high-accuracy fitting while adhering to the predetermined number of Gaussians. This makes subsequent organization into a structured voxel grid far more tractable, setting the stage for straightforward integration with standard 3D diffusion models. The choice to constrain the number of Gaussians is crucial, not only for structural simplicity but also for computational efficiency. It directly addresses the limitations of previous methods that struggled with the high dimensionality of unstructured radiance representations. Overall, the GaussianCube fitting algorithm represents a significant methodological contribution, demonstrating an effective balance between accuracy, efficiency, and suitability for 3D generative modeling.
3D Diffusion Model#
The application of diffusion models to 3D data presents unique challenges and opportunities. 3D diffusion models must address the higher dimensionality and complexity of 3D representations compared to images. This often leads to increased computational costs and challenges in training and sampling. However, the ability to generate high-fidelity, diverse 3D models makes this a very active area of research. Strategies to improve efficiency and scalability include using structured representations like voxel grids or point clouds to reduce the parameter count. Another significant challenge is the design of appropriate score functions or neural networks that are capable of capturing intricate details and long-range dependencies in 3D space. Successful approaches often leverage architectures like 3D U-Nets, while advanced sampling techniques, such as denoising diffusion implicit models, aim to improve sample quality and reduce computational burden. A key focus is on developing efficient and scalable diffusion models capable of generating diverse 3D outputs, conditioned or unconditioned, across a range of tasks, including object generation, avatar creation, and text-to-3D synthesis. Despite these challenges, the potential of 3D diffusion models to revolutionize 3D content creation is significant, offering an exciting avenue for future research and development.
Generative Modeling#
This research paper delves into the realm of 3D generative modeling, focusing on advancements in radiance field representations. The core contribution lies in introducing GaussianCube, a novel structured and fully explicit radiance representation designed to overcome limitations of existing methods. Previous approaches either relied on implicit feature decoders, which hinder modeling power, or employed spatially unstructured representations, making integration with standard 3D diffusion models challenging. GaussianCube addresses these issues by utilizing a novel densification-constrained Gaussian fitting algorithm and Optimal Transport for structured organization. This structured nature allows seamless integration with standard 3D U-Net architectures, simplifying the diffusion modeling process and achieving state-of-the-art results in various 3D generative tasks, including unconditional and class-conditioned object generation, digital avatar creation, and text-to-3D synthesis. The efficiency gains stem from significantly fewer parameters required compared to existing approaches, directly tackling the computational complexities often associated with high-dimensional 3D data. The paper emphasizes the versatility and high accuracy of the proposed method, positioning GaussianCube as a promising advancement in 3D generative modeling.
Experimental Results#
The experimental results section of a research paper is crucial for validating the claims made and demonstrating the efficacy of the proposed approach. A strong results section will present clear, well-organized data that directly addresses the research questions, using appropriate visualizations (graphs, tables, images) to present the information effectively. The discussion should go beyond simply stating the results; it should provide a thorough analysis, highlighting key findings and comparing the performance against existing methods using relevant metrics. Statistical significance tests should be employed to ascertain the reliability of the findings, and limitations or potential biases in the experimental setup should be honestly acknowledged. The writing style should be concise and objective, avoiding overly enthusiastic or subjective interpretations. Ideally, the results should be presented in a format that is both easy to understand and can easily be replicated by other researchers, allowing for validation and further development of the work. Including error bars or confidence intervals helps in determining the reproducibility of the results. Overall, this section must convincingly demonstrate the value and impact of the proposed method relative to the existing state-of-the-art.
Future Work#
Future research directions stemming from this GaussianCube work could explore several promising avenues. Improving efficiency in GaussianCube construction is crucial, potentially through algorithmic refinements or leveraging specialized hardware. Extending the model’s capabilities to handle more complex scenes and object interactions presents a significant challenge. Incorporating advanced techniques for handling dynamic scenes would significantly broaden the applicability. Another important area is to improve the model’s robustness to noisy or incomplete input data, crucial for real-world applications. Finally, investigating the potential of GaussianCube for novel applications such as interactive 3D modeling and animation would open up exciting new research possibilities. Ultimately, future work should focus on bridging the gap between high-fidelity 3D content creation and real-time interaction, making this technology more accessible and user-friendly.
More visual insights#
More on figures
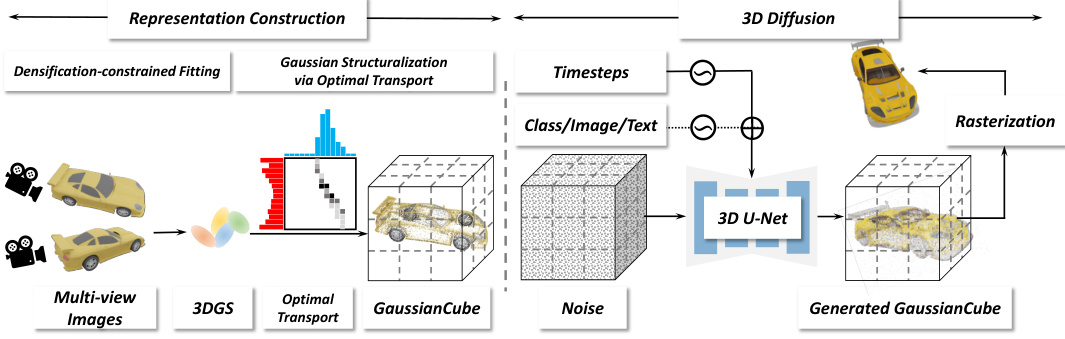
This figure illustrates the two-stage framework of the proposed method. The first stage is representation construction, which involves densification-constrained fitting of 3D Gaussians to a 3D asset from multi-view images using 3D Gaussian Splatting (3DGS) and then structuring these Gaussians into a GaussianCube using Optimal Transport. The second stage is 3D diffusion, where a 3D U-Net is used to generate a GaussianCube from noise, conditioned on class, image, or text information.
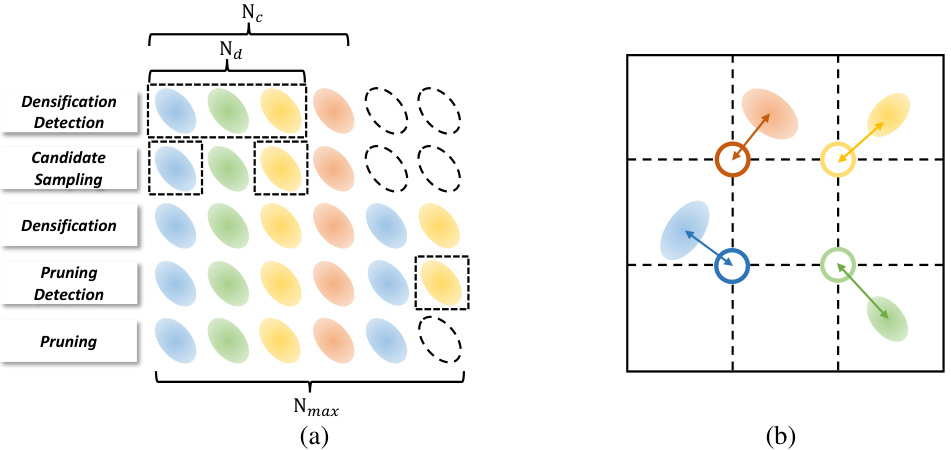
This figure illustrates the two main steps in creating the GaussianCube representation. (a) shows the densification-constrained fitting process, where the algorithm aims to obtain a fixed number of Gaussians while maintaining high accuracy. This involves identifying, sampling and adding Gaussians where needed (densification) and removing redundant ones (pruning). (b) demonstrates how the resulting Gaussians are organized into a structured grid using Optimal Transport, ensuring a spatially coherent arrangement for efficient 3D diffusion modeling.
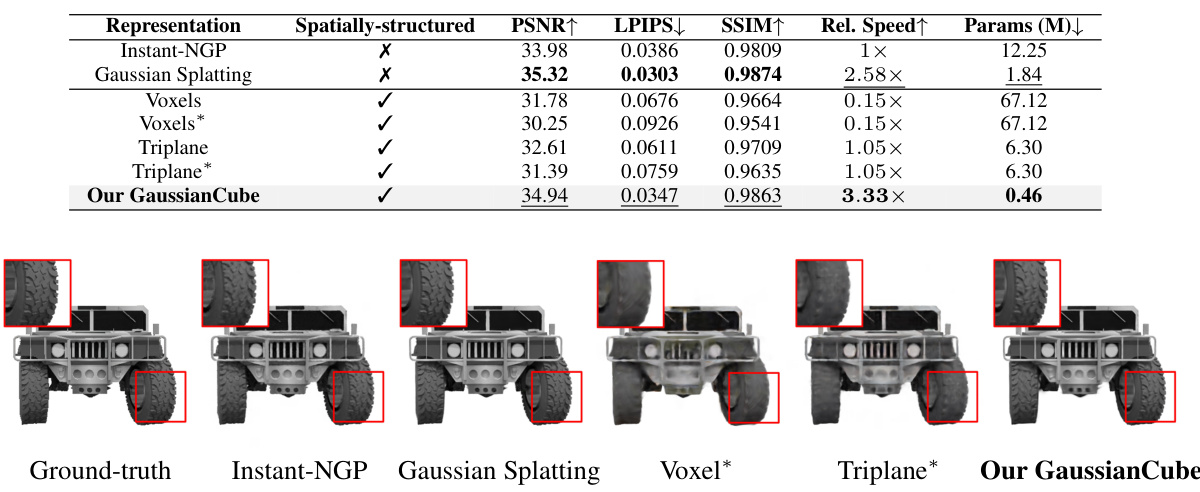
This figure shows a qualitative comparison of the object fitting results obtained using different methods: Instant-NGP, Gaussian Splatting, Voxel, Triplane, and the proposed GaussianCube. The results demonstrate the superior performance of GaussianCube in terms of detail preservation and overall accuracy compared to existing methods.

This figure compares the results of unconditional 3D generation of cars and chairs using four different methods: EG3D, GET3D, DiffTF, and the GaussianCube method proposed in the paper. Each method’s output is shown as a series of images depicting generated objects from different viewpoints. The GaussianCube method demonstrates the generation of objects with more complex geometry and finer details compared to the other methods.

This figure compares the results of class-conditioned 3D object generation using the proposed GaussianCube method against the DiffTF method on the OmniObject3D dataset. It showcases the ability of GaussianCube to generate objects with more complex geometries and detailed textures compared to DiffTF, demonstrating its superior performance in handling diverse object categories.

The figure compares the quality of 3D avatar generation from single frontal portraits using three methods: a reference image, Rodin [59], and the proposed GaussianCube method. The results show that GaussianCube produces avatars with higher fidelity and more detail, particularly in hair and accessories, compared to Rodin. The reference image is provided for comparison to show the level of detail achievable.
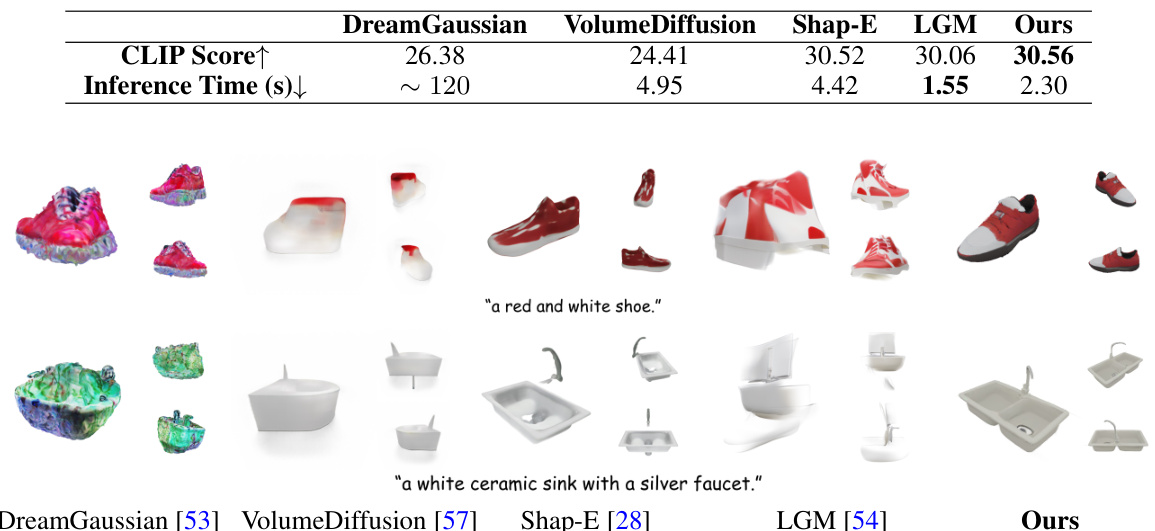
This figure compares the text-to-3D generation results of different methods on the Objaverse dataset. It showcases samples generated by DreamGaussian, VolumeDiffusion, Shape-E, LGM, and the authors’ method (Ours). The comparison highlights the superior quality and fidelity of the 3D objects generated by the authors’ approach, which closely match the given text descriptions.
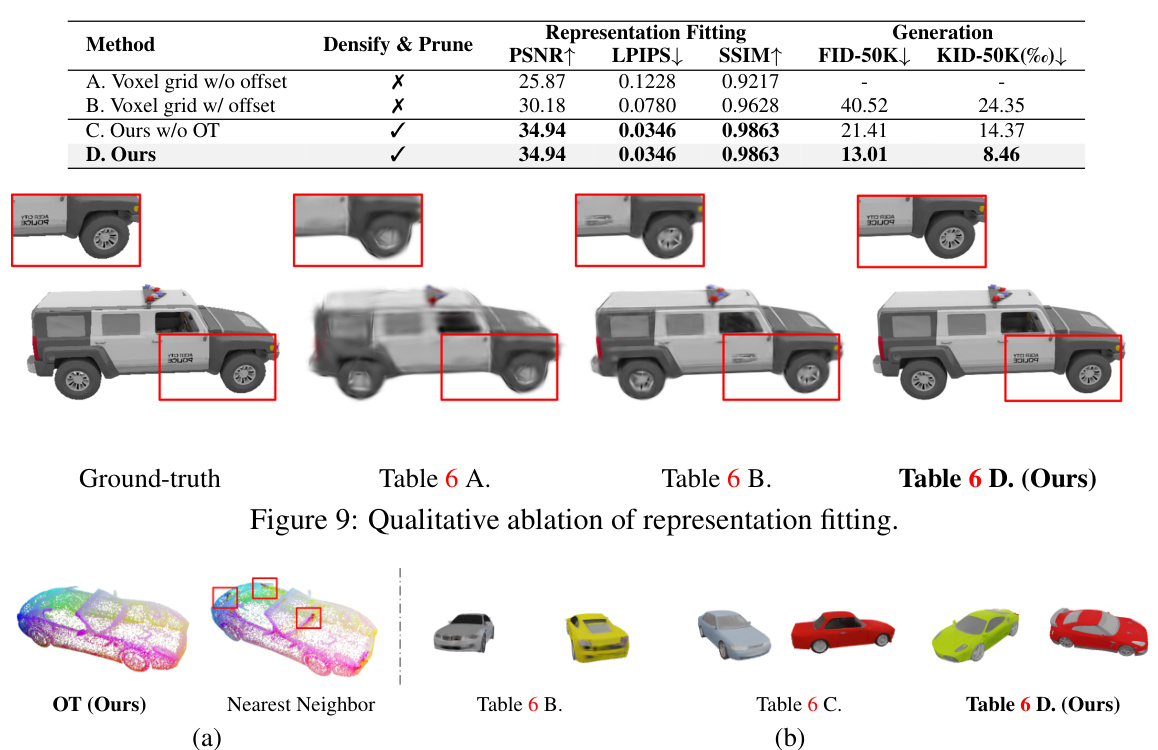
The figure shows a qualitative comparison of the object fitting results obtained using different representation construction methods. The methods compared are: (A) Voxel grid without offset; (B) Voxel grid with offset; (C) Our method without Optimal Transport; and (D) Our method (GaussianCube). The results demonstrate that the proposed GaussianCube method (D) significantly improves the fitting quality compared to the other methods.
This figure shows the qualitative results of ablation studies on representation fitting. It compares the results of several methods: a voxel grid without offsets, a voxel grid with offsets, the method without optimal transport (OT), and the full GaussianCube method (ours). Each image shows the fitting result for a car model. The figure visually demonstrates that the GaussianCube method (ours), which includes densification-constrained fitting and optimal transport, produces a significantly better fitting of the car model compared to other methods.

This figure shows the top-3 nearest neighbors for several generated samples using CLIP similarity. This demonstrates the model’s capability to generate novel objects with unique shapes and textures instead of simply memorizing training data.
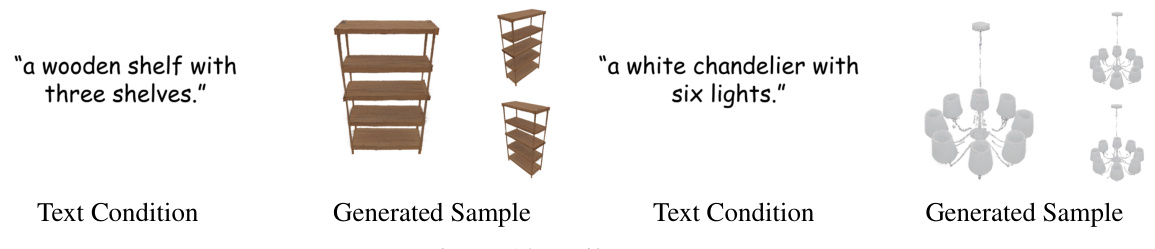
This figure shows examples of 3D objects generated by the GaussianCube model. The top three rows demonstrate the model’s ability to generate diverse objects with complex geometry and rich texture details from various conditions. The fourth row shows high-fidelity digital avatars generated from single portrait images. The fifth row showcases high-quality 3D assets generated from text prompts.

This figure showcases the versatility of the GaussianCube method in generating various 3D objects. The top three rows demonstrate the model’s ability to create objects with intricate details and textures from different categories (cars, chairs, and various other objects). The fourth row highlights the method’s capacity for high-fidelity digital avatar generation based on single input images. Finally, the bottom row showcases the successful generation of high-quality 3D models from text prompts, confirming the model’s ability to handle text-to-3D generation tasks.

This figure showcases the capabilities of the GaussianCube model in generating high-quality 3D assets. It presents examples of unconditional object generation, class-conditioned object generation, image-conditioned avatar generation, and text-to-3D generation. The results demonstrate the model’s ability to create diverse objects with complex geometries and rich details.

This figure compares the results of 3D avatar generation from a single frontal portrait image using three different methods: a reference image, the Rodin model, and the GaussianCube model proposed in the paper. The comparison shows that GaussianCube produces avatars with better details, particularly in hair and clothing textures, compared to the Rodin model. The GaussianCube method seems to generate more realistic results and preserve the identity better than Rodin.

This figure showcases the capabilities of the GaussianCube-based diffusion model. It presents several example outputs of the model conditioned on different inputs: unconditional generation (top three rows), image-conditioned avatar generation (fourth row), and text-conditioned 3D asset generation (fifth row). The figure highlights the model’s ability to generate diverse 3D objects with fine details and realistic textures, demonstrating its high accuracy and versatility.

This figure shows examples of 3D objects generated by the proposed GaussianCube method. The top three rows demonstrate the model’s ability to generate diverse objects with complex geometry and rich textures, based on different conditions (unconditional, text-to-3D, image-conditioned). The fourth row showcases the generation of high-fidelity digital avatars, conditioned on single portrait images. The bottom row illustrates the model’s success in creating high-quality 3D assets from text prompts.

This figure showcases the versatility of the GaussianCube model in generating various 3D objects. The top three rows demonstrate the generation of objects with complex geometries and rich details. The fourth row shows the creation of high-fidelity digital avatars conditioned on portrait images. Finally, the last row highlights the model’s capability in producing high-quality 3D assets from text prompts.

This figure demonstrates the text-guided 3D editing capabilities of the proposed GaussianCube model. Starting with a source object (a red pickup truck), the model successfully modifies the object’s attributes based on text prompts, generating variations such as a green pickup truck, a burnt and rusted pickup truck, and a pickup truck with a colorful paint job. This showcases the model’s ability to not only generate new 3D objects, but also to precisely control and manipulate existing ones through text-based instructions.

This figure showcases the results of the GaussianCube model on various 3D generation tasks. The top three rows demonstrate unconditional and text-to-3D object generation, highlighting the model’s ability to create diverse objects with intricate details and realistic textures. The fourth row displays its capability for high-fidelity digital avatar generation conditioned on single portrait images. Finally, the bottom row showcases the creation of high-quality 3D assets from text prompts, underlining the model’s versatility in handling different types of input and generating diverse outputs.

This figure showcases the model’s ability to generate a wide variety of 3D objects with high fidelity. The top three rows show examples of diverse objects with complex geometries and rich textures, generated unconditionally (ShapeNet Car, ShapeNet Chair, OmniObject3D) or conditioned on text prompts. The fourth row displays high-fidelity digital avatars generated from single portrait images, demonstrating the model’s ability to perform image-to-3D translation. The final row showcases text-to-3D generation, where high-quality 3D assets are generated based solely on text descriptions. This demonstrates the model’s versatility and capability in generating detailed and realistic 3D content across different modalities.

This figure showcases various examples of 3D objects generated using the GaussianCube method. The top three rows demonstrate the model’s ability to generate diverse objects with intricate details and textures. The fourth row shows high-fidelity digital avatars generated from single portrait images. The bottom row displays high-quality 3D models generated from text prompts.
More on tables

This table presents a quantitative comparison of the proposed GaussianCube method against existing state-of-the-art methods on three datasets: ShapeNet Car, ShapeNet Chair, and OmniObject3D. For each dataset, the table shows the Fréchet Inception Distance (FID) and Kernel Inception Distance (KID) scores, which are common metrics to evaluate the quality of generated 3D models. Lower FID and KID scores indicate better-quality generated models. The results demonstrate the superior performance of GaussianCube in generating high-fidelity 3D objects compared to the other methods.

This table presents a quantitative comparison of different methods for generating 3D digital avatars based on a single input portrait image. The metrics used for comparison include PSNR, LPIPS, SSIM, CSIM, FID-5K, and KID-5K. These metrics evaluate the quality of the generated avatars in terms of peak signal-to-noise ratio, learned perceptual image patch similarity, structural similarity index, cosine similarity of identity embedding, Fréchet inception distance and kernel inception distance, respectively. The results show that the proposed GaussianCube method significantly outperforms the other methods in terms of both visual quality and identity preservation.

This table compares the proposed GaussianCube method with several other 3D representations in terms of spatial structure, fitting quality (PSNR, LPIPS, SSIM), relative fitting speed, and the number of parameters. It highlights GaussianCube’s superior performance and efficiency, particularly when compared to methods using a shared implicit feature decoder.
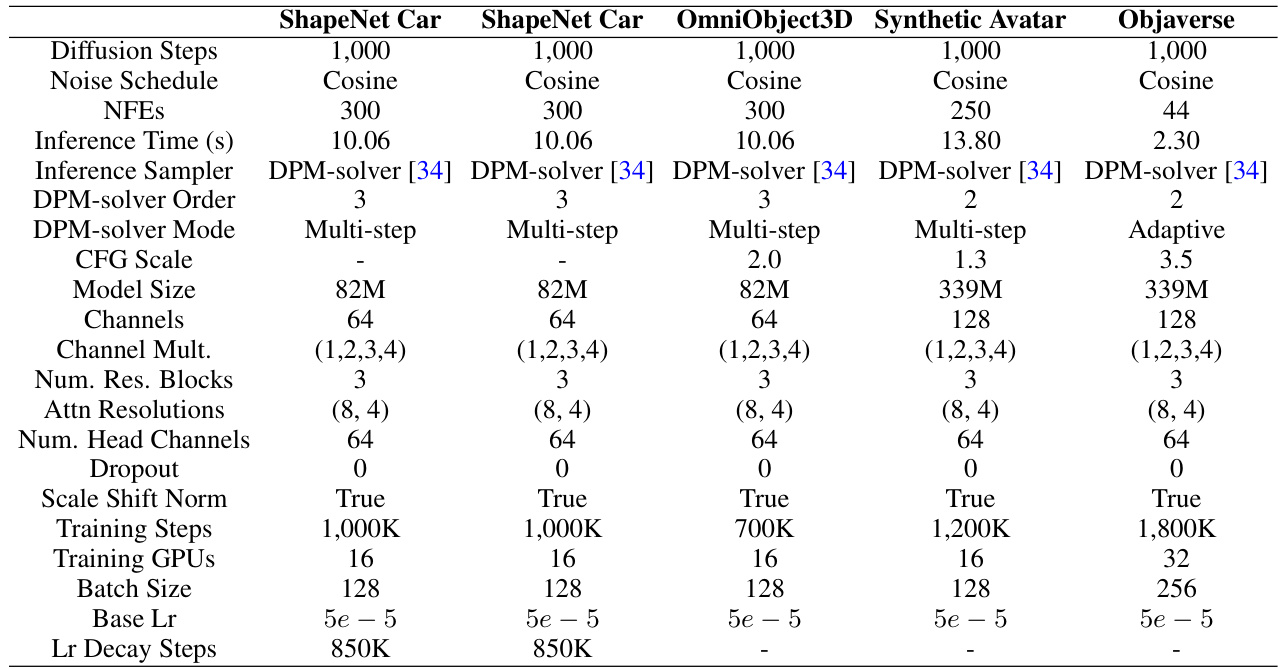
This table compares GaussianCube with other 3D representations in terms of spatial structure, fitting quality (PSNR, LPIPS, SSIM), relative fitting speed, and the number of parameters. It highlights GaussianCube’s superior performance and efficiency, especially when compared to methods using shared implicit feature decoders.
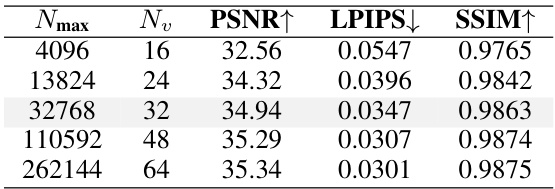
This table compares the proposed GaussianCube method with other 3D representations in terms of spatial structure, fitting quality (PSNR, LPIPS, SSIM), relative speed, and the number of parameters used. It highlights GaussianCube’s superior performance and efficiency, especially when compared to methods using shared implicit feature decoders.

This table compares GaussianCube against other 3D representations on the ShapeNet Car dataset. It shows the spatial structure, fitting quality (PSNR, LPIPS, SSIM), relative fitting speed, and the number of parameters for each method. It highlights that GaussianCube achieves comparable or better quality with significantly fewer parameters, especially when compared to methods using a shared implicit feature decoder.
Full paper#