Implicitly Guided Design with PropEn: Match your Data to Follow the Gradient

dhFHO90INk

Natasa Tagasovska et el.

TL;DR
#

Many scientific domains require generating new models or optimizing existing ones while meeting specific criteria. Traditional methods rely on generative models and discriminators, demanding large datasets which are often unavailable. This poses significant challenges, especially when dealing with complex landscapes.

The proposed framework, PropEn, addresses this limitation using a “matching” technique. It pairs each sample with a similar one having a better property value, thereby implicitly guiding the optimization process without training a discriminator. Combined with an encoder-decoder architecture, PropEn provides a domain-agnostic generative framework for efficient property enhancement. The method’s effectiveness is demonstrated across various applications, including protein design and airfoil optimization, with wet-lab validation for the former.

Key Takeaways
#

Why does it matter?
#

This paper is crucial for researchers in design optimization across various scientific domains. It offers a novel, data-efficient framework that significantly improves design optimization using a ‘matching’ technique, overcoming limitations of data-hungry models. The theoretical analysis and wet-lab validation strengthen its impact, opening new avenues for applications in various fields.

Visual Insights
#

This figure illustrates the difference between implicit and explicit guidance in design optimization. Implicit guidance (top) uses a matching technique to create a dataset where samples are paired with similar ones having a better property value. This matched dataset is then used to train an encoder-decoder model which implicitly learns the direction of improvement. In contrast, explicit guidance (bottom) trains separate generator and discriminator models to explicitly guide the optimization process in the latent space. The figure highlights how PropEn uses implicit guidance to overcome the limitations of data-hungry explicit methods.

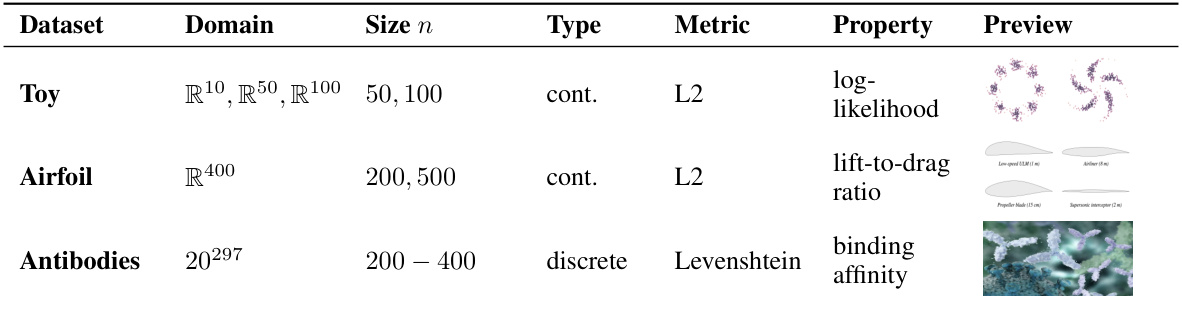
This table provides a summary of the datasets used in the experiments section of the paper. It includes information about the domain of each dataset, the number of samples (size n), the type of data (continuous or discrete), the metric used for evaluation, the property being optimized, and a visual preview of the data.

In-depth insights
#

Implicit Guidance
#

Implicit guidance in the context of machine learning for design optimization offers a powerful alternative to traditional explicit methods. Instead of using a separate discriminator to explicitly guide a generative model, implicit guidance leverages the inherent structure of the data to implicitly steer the optimization process. By matching samples with similar ones exhibiting better property values, the method crafts a training dataset that inherently points towards improvement. This approach is particularly attractive when dealing with limited datasets and complex design spaces, because it circumvents the need for training a data-hungry discriminator. Furthermore, by focusing on matched pairs, implicit guidance keeps the generated designs within the realm of plausible solutions, mitigating the risk of unrealistic outputs often associated with explicit methods. The theoretical underpinnings suggest that this matching strategy approximates the gradient of the property of interest, offering a computationally efficient method to enhance properties. PropEn, the proposed framework, demonstrates the effectiveness and competitiveness of this implicit approach across several domains, including protein design and airfoil optimization, solidifying its value as a robust and versatile technique for guided design in scenarios with limited data.

Matching Datasets
#

The concept of ‘Matching Datasets’ is crucial for effective data augmentation and implicit guidance in machine learning, particularly when dealing with limited data. The core idea revolves around pairing each data point with a similar one possessing a superior property value. This matching process implicitly encodes the direction of improvement, effectively creating a larger dataset that guides the learning process without explicit supervision. The effectiveness of matching hinges on the choice of appropriate metrics for measuring similarity and the definition of superior property. A careful selection is paramount to avoid introducing bias or selecting non-representative matches. The generated matched dataset serves as the basis for training a model, often an encoder-decoder architecture, that learns to generate new designs that are similar to the input yet exhibit enhanced properties. This method avoids the need for a discriminator, which is often problematic in data-scarce scenarios, thus improving efficiency and robustness. Theoretical analysis can reveal how well the gradient of the desired property is approximated during training using this matched dataset. However, the matching approach has computational cost and limitations, making the selection of appropriate metrics crucial for balancing these aspects.

Gradient Approx.
#

Approximating gradients efficiently is crucial for many machine learning applications, especially when dealing with limited data or complex, high-dimensional spaces. The core idea revolves around cleverly using a matched dataset to implicitly estimate the gradient direction. Matching pairs of similar data points, where one exhibits a superior property value, creates a dataset that inherently points towards improvement. This circumvents the need for explicit gradient calculations or training of a discriminator, a significant advantage when data is scarce. The theoretical analysis likely demonstrates that training on this matched dataset leads to a model that implicitly learns an approximation of the gradient, achieving efficient design optimization. A key aspect is likely the theoretical justification showing this approximation accurately reflects the true gradient, providing a sound foundation for the approach. This is especially important given the focus on limited data scenarios, where traditional methods might fail due to their high data requirements. The effectiveness and competitive advantages would be established through rigorous experiments and evaluations.

Design Optimization
#

Design optimization, a core theme in the provided research paper, focuses on enhancing the properties of existing designs or generating new ones that meet specific criteria. The paper advocates for implicit guidance, contrasting it with traditional methods that rely on explicit guidance using discriminators. This novel approach avoids the need for large datasets which is beneficial for real-world scientific applications with limited data. Matching techniques are employed to create a larger training dataset, implicitly indicating the direction of improvement. The authors demonstrate that training on this matched dataset approximates the gradient of the desired property, leading to efficient optimization. The methodology proves domain-agnostic, applicable across various scientific fields, as shown through evaluations in toy problems and real-world applications including protein design and airfoil optimization. Wet lab validation further supports the effectiveness of the proposed method, showcasing its practical utility and competitiveness against common baselines.

Future Works
#

The “Future Works” section of this research paper on implicitly guided design using PropEn presents exciting avenues for expansion. Extending PropEn to handle multi-property optimization is crucial, allowing for the simultaneous enhancement of multiple design characteristics. This requires careful consideration of potential trade-offs between properties and sophisticated methods for handling conflicting optimization goals. Exploring various similarity metrics beyond Euclidean distance could significantly improve PropEn’s performance on different data modalities, especially those with complex or non-Euclidean structures. Applying PropEn to other domains, such as materials science and small molecule design, will demonstrate its generalizability and broad applicability, particularly when datasets are limited. Finally, developing a multi-property PropEn framework is essential, allowing for a comprehensive optimization strategy considering the interconnectedness of various design attributes. This can substantially enhance its effectiveness and utility, enabling the generation of truly superior and more robust designs across a wider range of application domains.

More visual insights
#

More on figures

This figure shows the results of PropEn on a pinwheel toy dataset with 72 training examples. The left panels (a) and (b) illustrate the optimization trajectories for in-distribution (IID) and out-of-distribution (OOD) seed designs, respectively. The grey circles represent the training data, colored by the property value. The pink points are the initial held-out test points, and the orange ‘x’ markers show the optimization trajectories generated by PropEn. The color intensity of the ‘x’ markers increases with each optimization step, demonstrating improvement in the property value. The right panel (c) shows the sum of the negative log-likelihoods (NLL) of the seed and optimized designs over the optimization steps. This plot visually demonstrates the trajectory of PropEn optimization and its ability to improve the property value while remaining within the data distribution for IID seeds and leveraging the closest regions in the data distribution for OOD seeds.

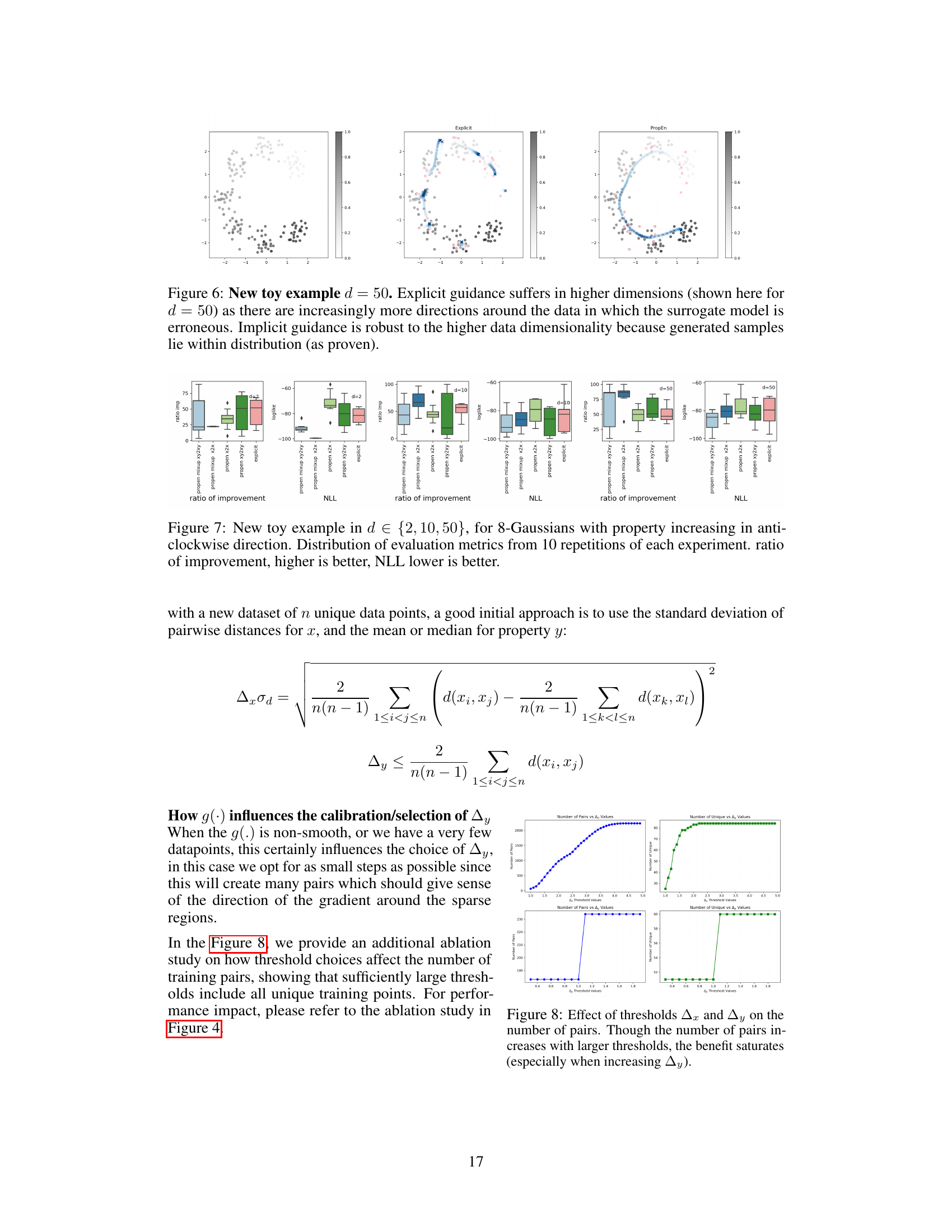
This figure shows the results of PropEn on two toy datasets, 8-Gaussians and Pinwheel, in 50 and 100 dimensions. The results from 10 independent runs of each experiment are shown as distributions for ratio of improvement and negative log-likelihood (NLL). The figure helps visualize the performance of PropEn compared to explicit guidance in higher-dimensional spaces.

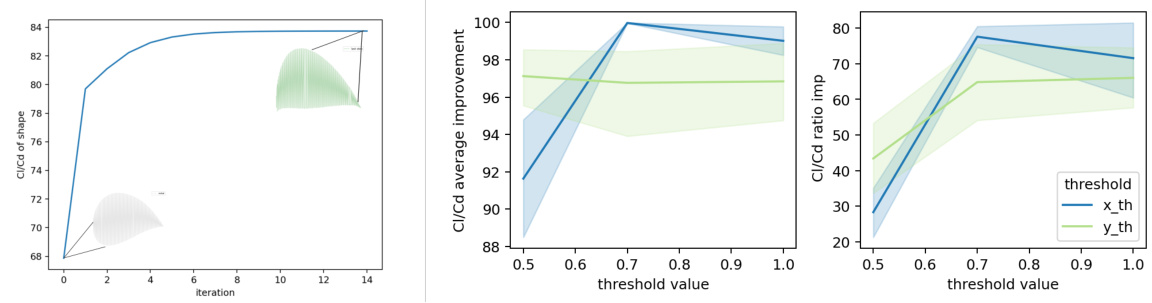
This figure presents ablation studies on the airfoil optimization task using PropEn. Panel (a) shows that PropEn consistently improves the lift-to-drag ratio (Cl/Cd) over multiple iterations while generating realistic airfoil shapes. Panels (b) and (c) analyze the impact of the matching thresholds ∆x and ∆y on PropEn’s performance. These thresholds control the size of the matched dataset by defining the allowed differences in airfoil shape and Cl/Cd between paired samples. The results indicate how the choice of thresholds influences the optimization process.

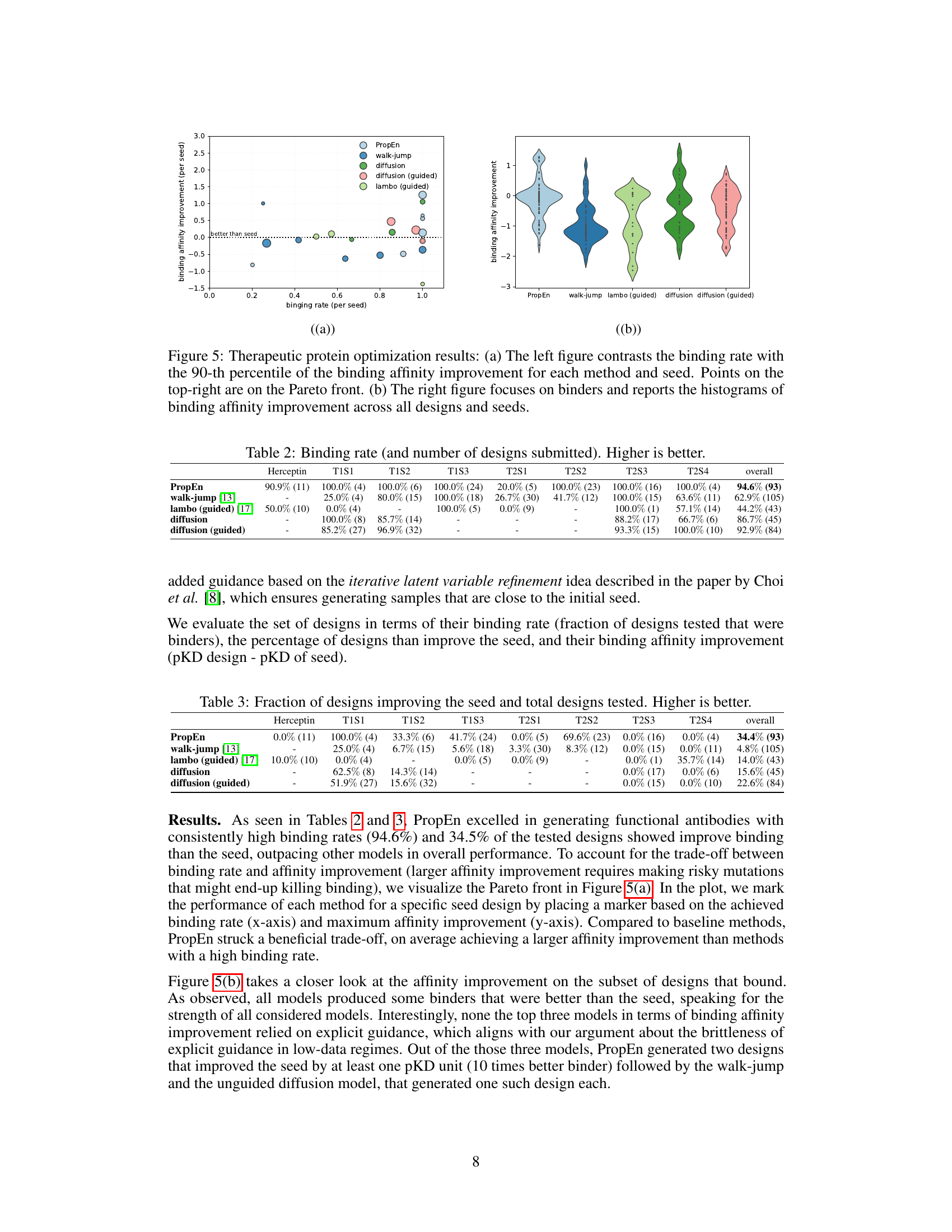
This figure shows the results of therapeutic protein optimization experiments. Panel (a) is a scatter plot showing the trade-off between binding rate and binding affinity improvement for different methods, including PropEn. Points in the top-right quadrant represent the best balance of high binding rate and high affinity improvement. Panel (b) displays violin plots showing the distribution of binding affinity improvements for each method, focusing only on the designs that successfully bound to the target.

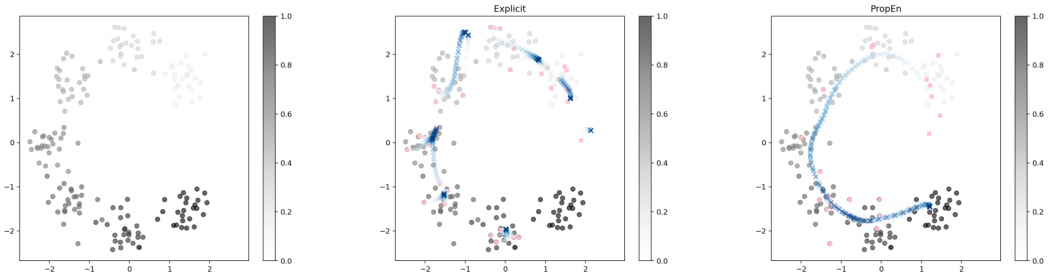
This figure shows the results of applying PropEn to a pinwheel-shaped dataset with 72 training examples. The left panel displays the training data points, colored by their property values (size). Pink points represent initial test points, and orange ‘x’ points show the trajectory of PropEn optimization. The color intensity of the trajectory points increases with each iteration, indicating improvement in the property. The right panel shows the negative log-likelihood (NLL) of the initial seeds and the optimized designs across the optimization steps. It demonstrates that PropEn successfully improves the design and remains within the data distribution.

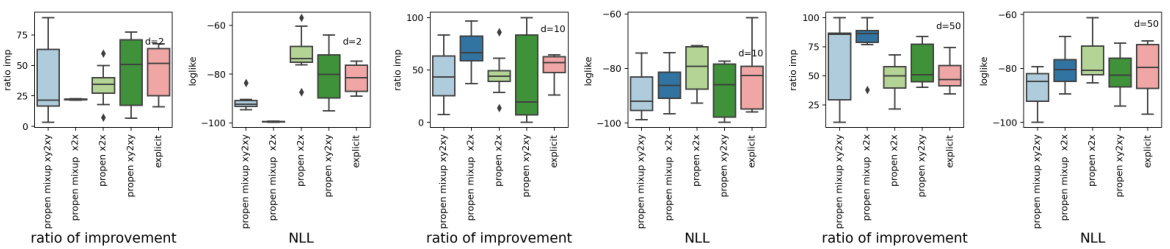
This figure shows the results of experiments using PropEn on two toy datasets, 8-Gaussians and Pinwheel, with dimensionalities of 50 and 100. It displays the distribution of evaluation metrics (ratio of improvement and negative log-likelihood) across 10 repetitions of each experiment. This visualization helps in understanding the performance consistency of PropEn across different settings and datasets. The results demonstrate PropEn’s superiority over explicit guidance methods.

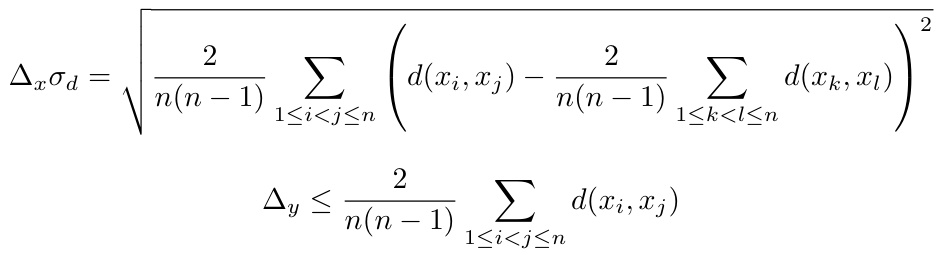
This figure shows the performance comparison between PropEn and explicit guidance methods on 8-Gaussians and pinwheel toy datasets with dimensionality 50 and 100. The boxplots illustrate the distribution of different evaluation metrics (ratio of improvement and negative log-likelihood) across ten repetitions of each experiment for each method. It aims to demonstrate PropEn’s effectiveness and advantages, particularly in higher dimensional spaces, compared to traditional explicit guidance.

This figure presents the results of PropEn on two toy datasets (8-Gaussians and Pinwheel) with different dimensionalities (d = 50 and d = 100). The results of 10 independent runs are shown to highlight the variability of PropEn’s performance. It shows the distribution of the ratio of improvement and the negative log-likelihood (NLL) across multiple runs for each setting. This demonstrates PropEn’s robustness across different settings and its effectiveness in improving the property of interest.

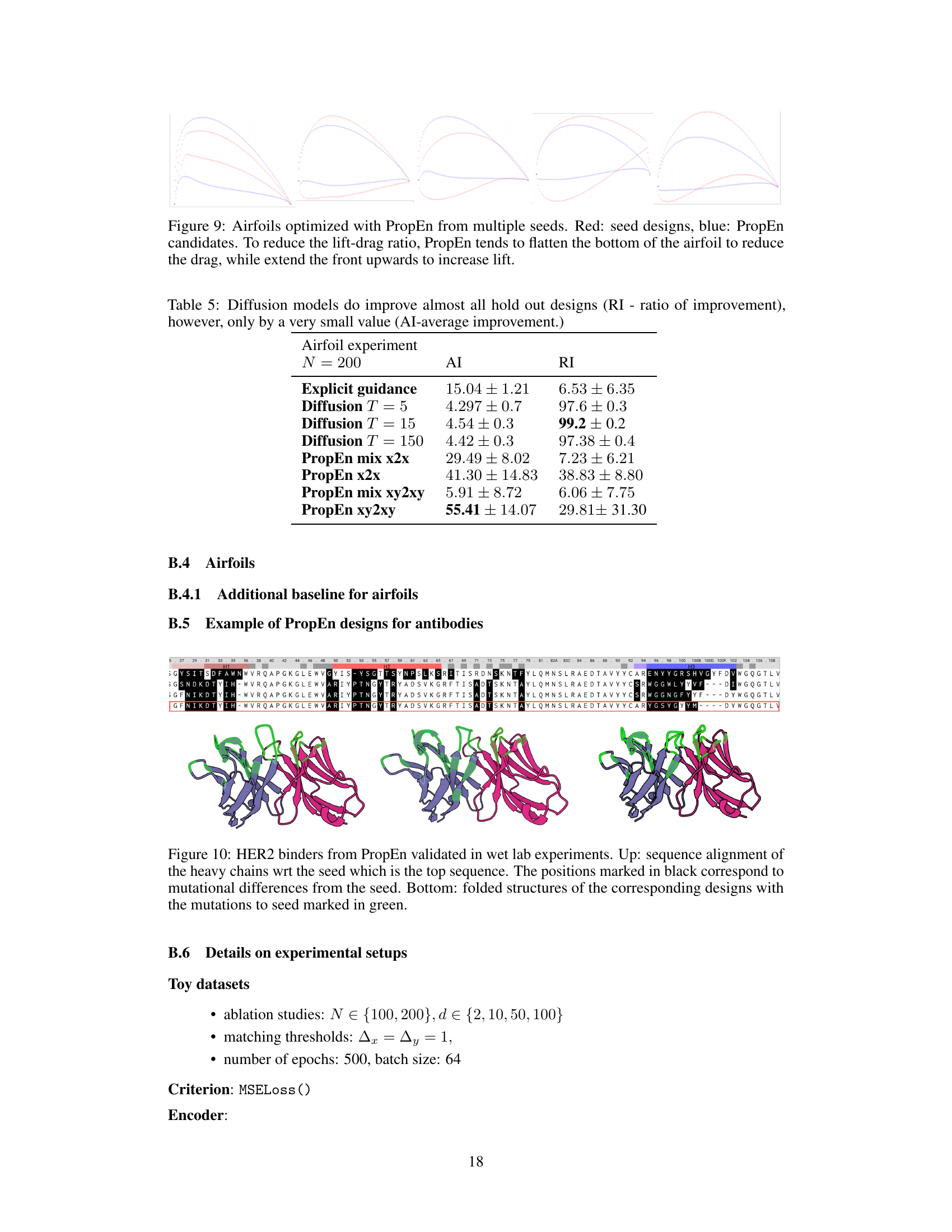
This figure shows the results of wet lab experiments validating the designs generated by PropEn for HER2 binders. The top part shows the sequence alignment of the heavy chains of the designed antibodies with the original seed sequence, highlighting the mutations introduced by PropEn. The bottom part shows the 3D folded structures of the designed antibodies, with the mutations shown in green. This figure demonstrates the ability of PropEn to generate novel and functional antibody designs.