↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Understanding how deep neural networks (DNNs) make decisions is a major challenge in explainable AI. Existing methods for interpreting DNNs often lack faithfulness, failing to accurately reflect the network’s internal logic. This paper addresses these issues by focusing on the concept of ‘interactions’ between input variables, which represent fundamental inference patterns within the DNN. Early work empirically observed that DNNs learn interactions in two phases: initially, simpler interactions are favored, followed by the learning of more complex ones, often leading to overfitting.
This research rigorously proves the two-phase dynamics of interaction learning. The authors introduce a mathematical framework that explains how a DNN’s generalization power changes throughout training. They derive an analytic solution that accurately predicts the real dynamics of interactions across different DNN architectures and tasks. This theoretical framework provides deeper insights into DNN behavior, particularly regarding the transition from underfitting to overfitting, leading to new approaches for enhancing DNN performance and interpretability.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in deep learning and explainable AI. It provides a theoretical foundation for understanding how deep neural networks learn interactions, bridging the gap between empirical observations and theoretical understanding. This opens new avenues for improving the generalization and robustness of DNNs and developing more faithful explanation methods.
Visual Insights#
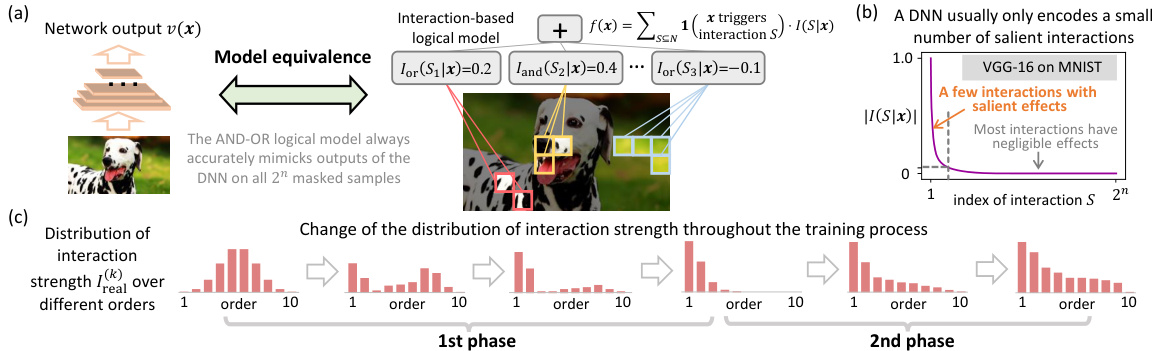
This figure illustrates three key concepts of the paper. (a) shows the equivalence of a DNN’s inference to a logical model using AND-OR interactions. (b) demonstrates the sparsity of interactions, highlighting that only a few have significant effects. (c) visually represents the two-phase learning dynamics of DNNs: a first phase where low-order interactions are dominant, and a second phase where high-order interactions emerge.

This table summarizes the mathematical settings used for calculating interactions, including the output function used by the DNN, the threshold for determining salient interactions, and the baseline values used for masking input variables. Different strategies are used for image data (zero baseline on the feature map after ReLU), text data (using the [MASK] token), and point cloud data (using the cluster center of each point cluster).
In-depth insights#
DNN Interaction Dynamics#
Analyzing DNN interaction dynamics reveals crucial insights into model behavior and generalization. The two-phase learning process, initially characterized by a wide distribution of interaction complexities, progresses to prioritize low-order interactions before gradually incorporating higher-order ones. This shift reflects a transition from underfitting (removal of noise interactions) to overfitting (learning complex, non-generalizable patterns). Mathematical proofs provide theoretical grounding for the observed dynamics, emphasizing the link between interaction complexity and generalization power. Further research could explore variations in this dynamic based on network architecture and task type, potentially leading to more robust and interpretable DNN models. Understanding the interplay between sparsity, transferability, and the two phases offers a promising avenue for improving DNN efficiency and trustworthiness.
Two-Phase Learning#
The concept of “Two-Phase Learning” in the context of deep neural networks (DNNs) learning symbolic interactions is a significant contribution. The first phase focuses on pruning high-order interactions, which are less generalizable and prone to overfitting. This phase leads to a model that encodes primarily simpler, more robust interactions, thus improving generalization. The second phase, however, sees the emergence of increasingly complex interactions. Although this might initially seem counterintuitive, it reflects the DNN’s attempt to fine-tune its understanding of the data. This two-phase dynamic explains the transition from underfitting to overfitting, offering valuable insights into DNN training processes and the role of interaction complexity. Mathematical proof supporting these phases further solidifies the finding’s significance. The theoretical framework provides a mechanism to predict the dynamics of interactions during training, potentially informing strategies for improving model generalizability and robustness.
Interaction Sparsity#
Interaction sparsity, a central concept in the provided research, reveals that deep neural networks (DNNs) surprisingly rely on a small subset of interactions between input variables to make predictions. This sparsity contrasts with the vast number of potential interactions, implying an efficient encoding of information. The faithfulness of post-hoc explanations, often doubted due to the complexity of DNNs, is surprisingly supported by this finding: a small set of interactions accurately captures the DNN’s inference logic. The research explores the dynamics of this sparsity during training, showing a two-phase evolution. Initially, the DNN focuses on low-order interactions. Later, it incorporates higher-order ones, which are more complex but potentially prone to overfitting. This two-phase model offers a powerful framework for understanding generalization and overfitting in DNNs. By focusing on the essential interactions, this research contributes to both a better comprehension of DNN internal workings and enhanced methods for their interpretation.
Theoretical Analysis#
A theoretical analysis section in a research paper would rigorously examine the core concepts and mechanisms of the presented work. It would likely involve mathematical modeling to represent the system’s behavior and derive key properties, potentially using theorems and proofs to establish the validity of claims. The analysis might explore limiting cases or boundary conditions to highlight the robustness of the model. Furthermore, it could delve into the underlying assumptions and their implications, acknowledging potential limitations or areas where further research is needed. A strong theoretical analysis would provide a solid foundation for the presented findings and contribute significantly to the field’s understanding of the phenomenon under investigation, ultimately strengthening the paper’s overall contribution.
Future Research#
Future research directions stemming from this two-phase dynamics study could involve developing more sophisticated noise models to better capture the nuances of the training process and improve the accuracy of theoretical predictions. Further exploration into the interplay between network architecture and the two-phase dynamics is warranted. Investigating whether specific architectural choices influence the duration or characteristics of each phase would provide valuable insights into DNN design. Finally, extending the theoretical framework to encompass other types of interactions beyond AND-OR relationships, and applying the findings to different learning paradigms (e.g., reinforcement learning) are promising avenues for future work. The generalizability of the two-phase dynamics across various tasks and datasets should be further investigated, focusing on applications beyond image and text processing.
More visual insights#
More on figures
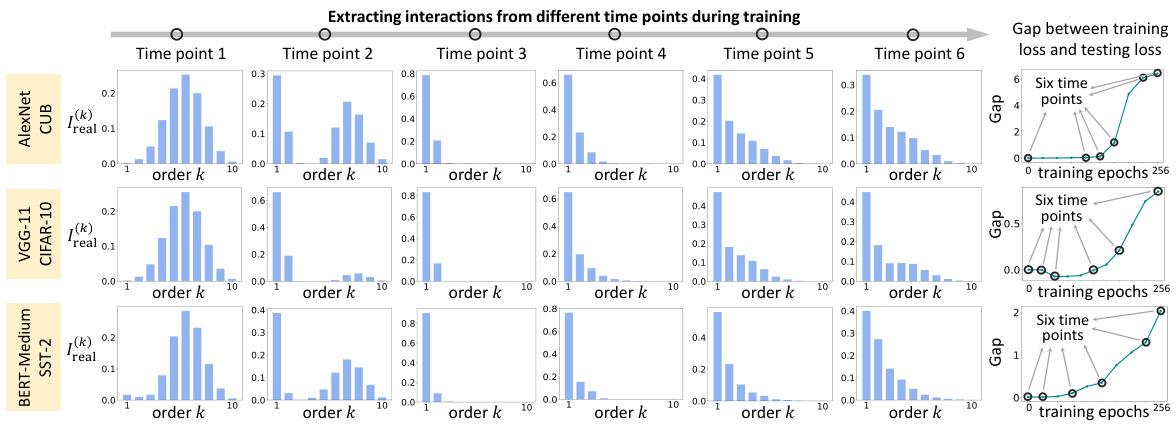
This figure demonstrates the two-phase dynamics of interaction complexity during the training process of various deep neural networks (DNNs). Each row represents a different DNN trained on a different dataset. The x-axis represents the order (complexity) of the interactions, and the y-axis represents the interaction strength. The figure shows how the distribution of interaction strength changes over six different time points during training. Before training, the DNNs primarily encode interactions of medium complexity. In the first phase, low-order interactions are emphasized while high-order interactions are suppressed. In the second phase, high-order interactions gradually increase, indicating a shift towards overfitting. The timing of the transition to the second phase aligns with the point where the gap between training and testing loss begins to increase.

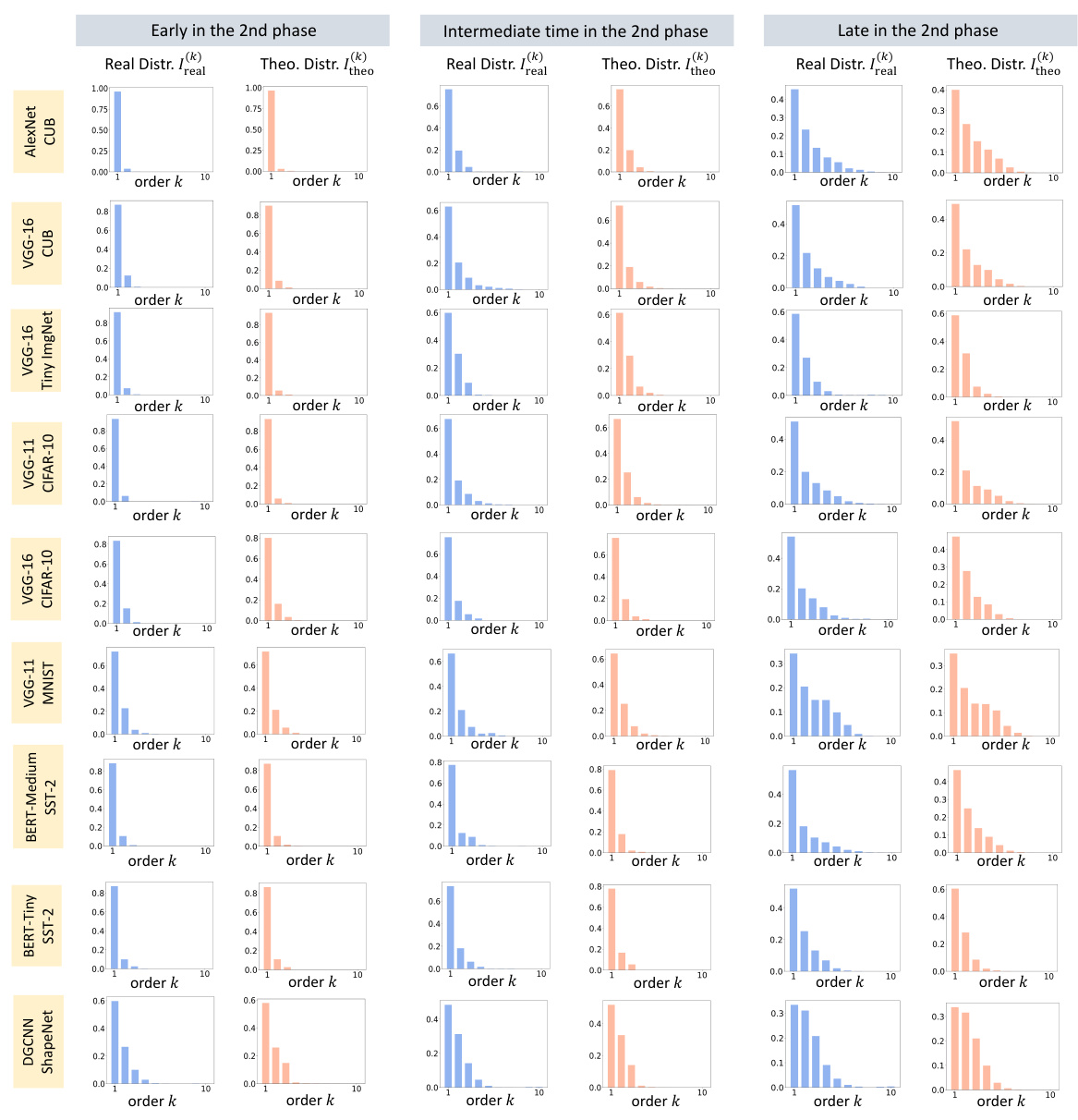
This figure shows the curves of r(k) (the ratio of the strength of low-order interactions to that of high-order interactions) with different σ² (noise levels) and n (number of variables). The curves demonstrate that the ratio r(k) monotonically increases with σ². This result supports Proposition 1, which states that as the noise level decreases during training, the relative strength of low-order interactions compared to high-order interactions also decreases.
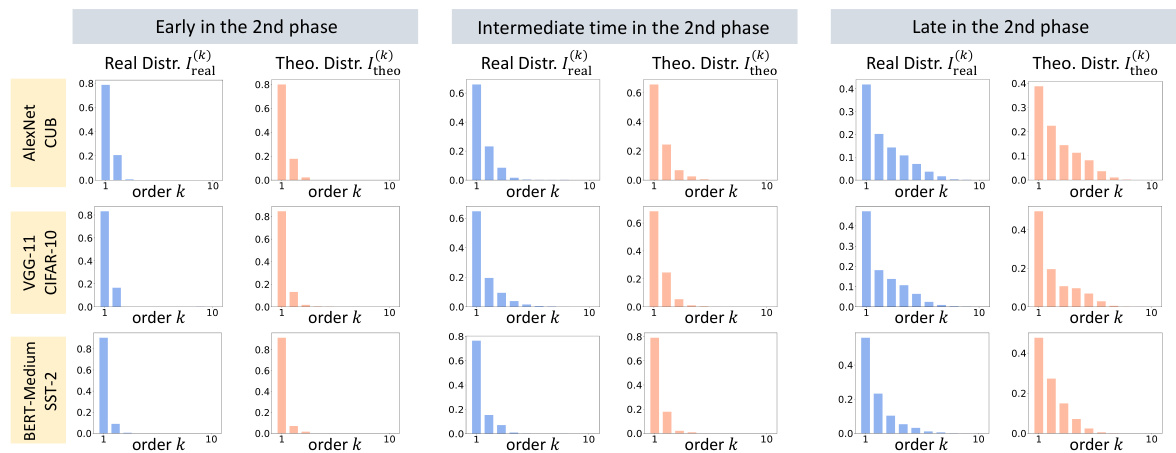
This figure demonstrates the two-phase dynamics of interaction complexity during DNN training across various datasets and architectures. Each row displays the distribution of interaction strength (I(k)) across different orders (k) at various training epochs. The figure highlights the two phases: an initial phase where the DNN primarily removes interactions of medium to high complexity and a second phase where it gradually learns increasingly complex interactions. The onset of the second phase correlates with an increase in the gap between training and testing loss.
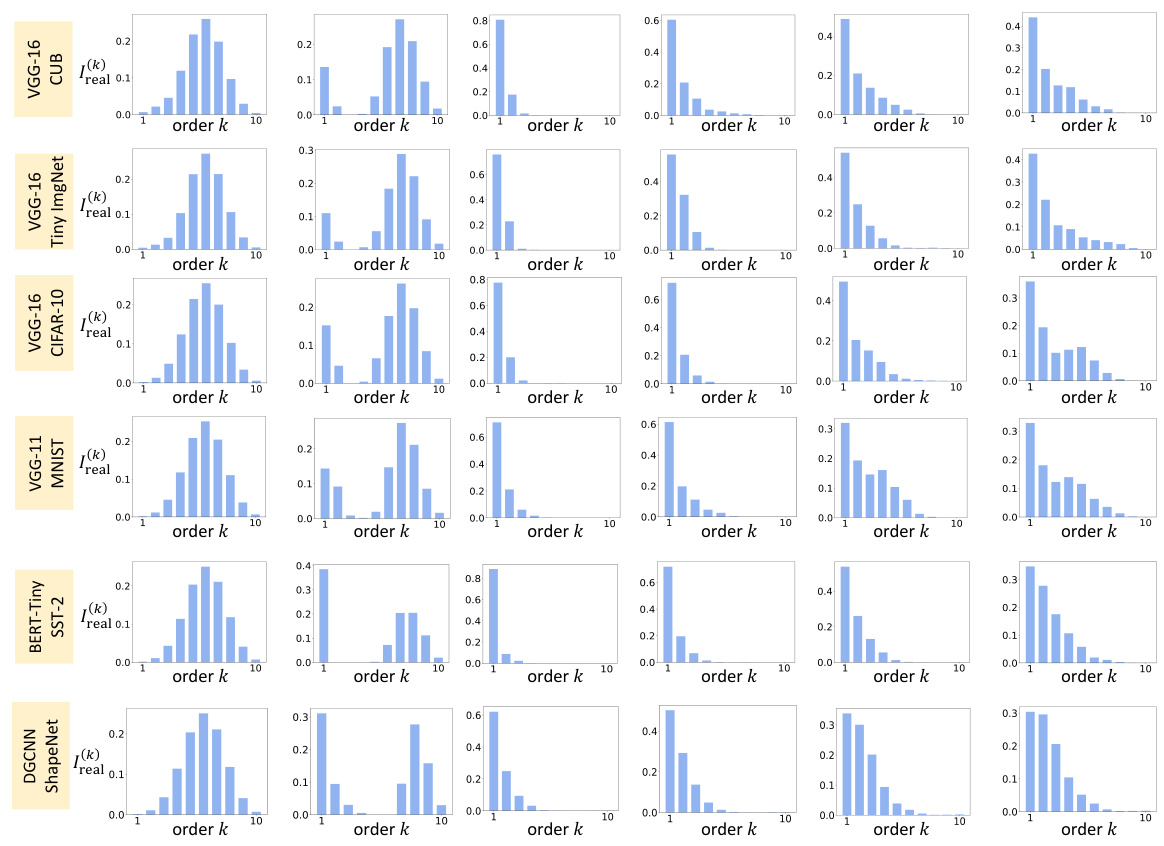
This figure shows how the distribution of interaction strength changes over different orders (k) during the training process of various DNNs on different datasets. Each row represents a different DNN trained for a different task. The plots show that in the initial state before training, the distribution has a spindle shape, with medium-order interactions being most prominent. Then, a two-phase dynamic is observed in all DNNs. In the first phase, medium and high-order interactions are removed, leaving only low-order interactions. In the second phase, higher-order interactions are gradually learned. The beginning of the second phase coincides with the increase of loss gap between training and testing loss, which indicates the start of overfitting. This provides empirical evidence supporting the theory proposed in the paper that DNNs learn interactions in two phases.
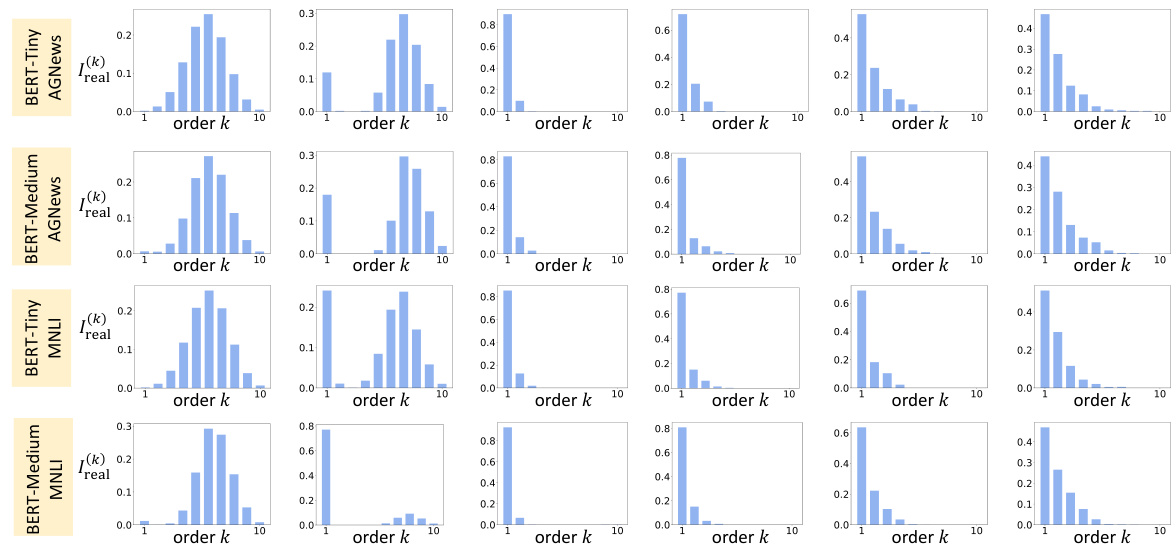
This figure shows how the distribution of interaction strength changes during the training process for various DNNs trained on different datasets. Each row represents a different DNN and dataset, and the columns show the distribution of interaction strength at different time points during training. The figure demonstrates a two-phase dynamic, with an initial phase where the DNN eliminates interactions of medium and high complexity, and a second phase where the DNN gradually learns interactions of increasing complexity. The onset of the second phase coincides with an increase in the gap between training and testing loss, suggesting a transition from underfitting to overfitting.
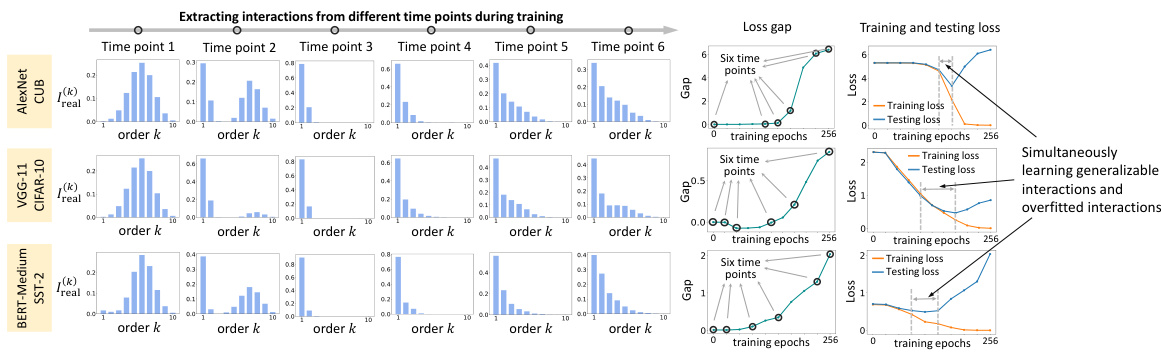
This figure demonstrates the training and testing loss curves, along with the loss gap and the distribution of interaction strength across different orders. Each row represents a different DNN trained on a different dataset. The figure illustrates how the two phases of interaction learning relate to the training and testing loss curves. The loss gap is the difference between the training and testing loss, reflecting generalization performance. In the first phase, the loss gap decreases as the DNN learns more generalizable low-order interactions, and in the second phase, the loss gap increases as the DNN begins to learn more complex, high-order interactions which are typically less generalizable, indicating overfitting.

This figure shows the distribution of interaction strength (I(k)) across different orders (k) during the training process for several DNNs. Each row represents a different DNN trained on a different dataset. The plots visualize the shift in the distribution from a relatively even distribution before training to a two-phase pattern during training. The first phase shows a decrease in medium and high-order interaction strength, while the second phase shows an increase in higher-order interactions. The timing of the transition between these two phases aligns with when the gap between training and testing loss increases, suggesting a connection to overfitting.
This figure shows how the distribution of interaction strength changes over different orders (complexity) throughout the training process for several different DNNs trained on various datasets. It demonstrates the two-phase dynamics of interaction learning observed in the paper. Before training, medium-complexity interactions dominate. Then, in phase one, the DNN removes medium- and high-complexity interactions and prioritizes low-order interactions. In phase two, it gradually learns higher-order interactions. The onset of phase two correlates with the point where the difference between training and testing loss begins to increase (the loss gap).
Full paper#



















