↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current training-free guided diffusion methods struggle with complex constraints, often resulting in lower-quality generations, particularly when using a limited inference budget. These methods typically alternate between diffusion steps and gradient steps for loss-guided optimization, resulting in suboptimal results. They are also sensitive to initialization, and performance drops significantly when using fewer function evaluations.
Trust Sampling tackles these issues with a novel approach. Instead of alternating between steps, it formulates each diffusion timestep as an independent optimization problem. This allows for multiple gradient steps on a proxy constraint function, continuing until the proxy becomes unreliable. Additionally, it incorporates a method for early termination when the sample diverges from the model’s state manifold. This approach leads to improved generation quality and efficiency across diverse domains (images and 3D motion), significantly outperforming existing methods in terms of fidelity and constraint satisfaction, even with fewer computations.
Key Takeaways#
Why does it matter?#
This paper is important because it offers a novel and effective method for guided diffusion, addressing current limitations in satisfying challenging constraints during generation. It presents a flexible and efficient framework applicable across diverse domains, improving generation quality and showing significant advancements over existing methods. This opens new avenues for research in training-free constrained generation and has implications for various applications involving complex generative tasks.
Visual Insights#

The figure shows examples of image and human motion tasks where Trust Sampling can be applied. For image tasks, super-resolution, inpainting, and Gaussian deblurring are demonstrated. For human motion tasks, hand and foot tracking, and obstacle avoidance are shown. These examples highlight the method’s versatility across various constraint problems in different domains.
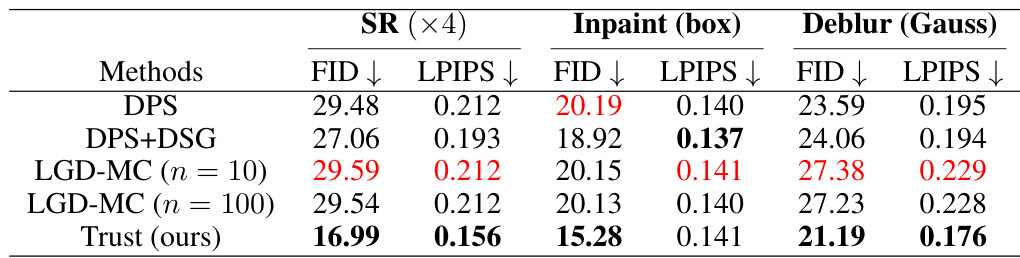
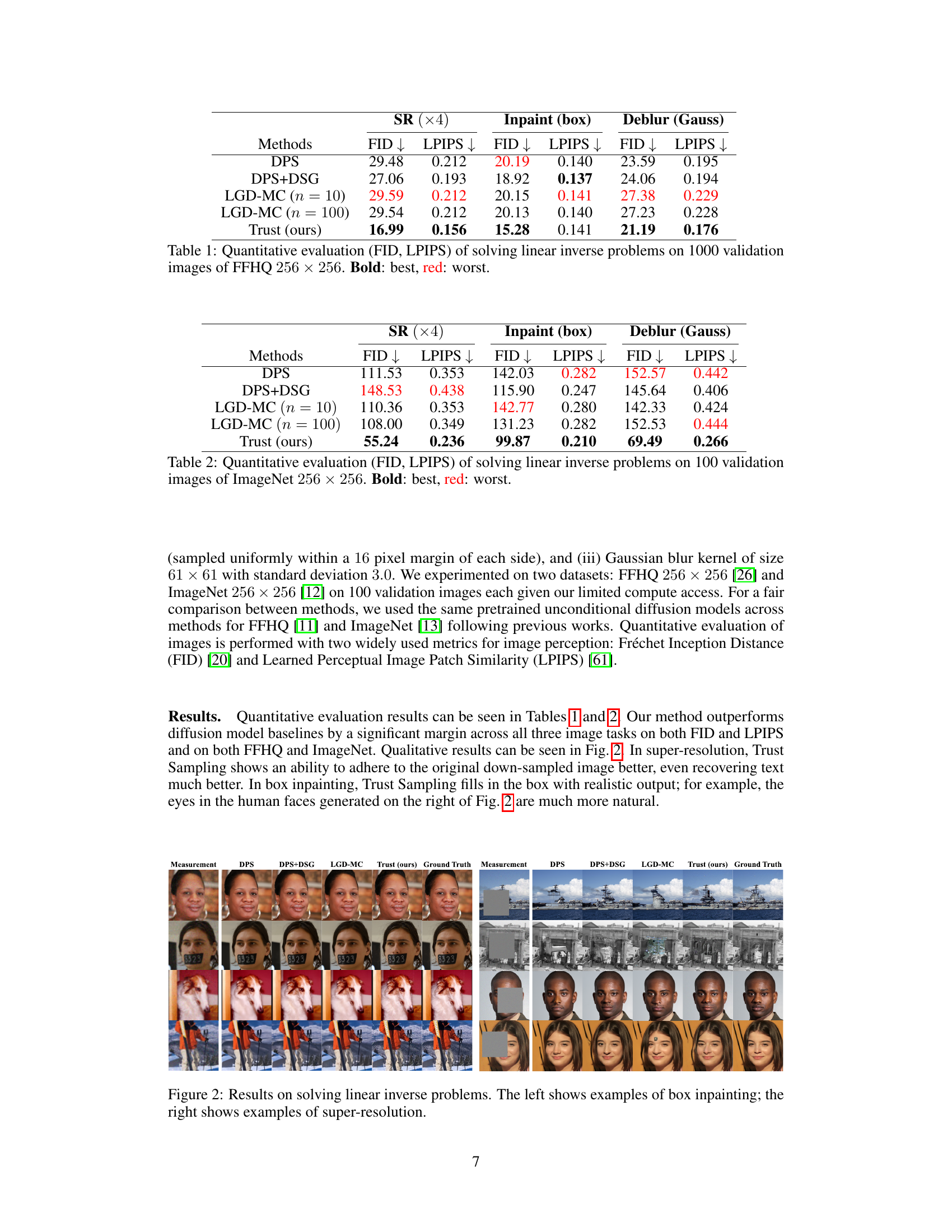
This table presents a quantitative comparison of different methods for solving three linear inverse problems (Super-Resolution, Inpainting, and Deblurring) on the FFHQ dataset. The performance is measured using two metrics: Fréchet Inception Distance (FID) and Learned Perceptual Image Patch Similarity (LPIPS). Lower scores indicate better performance. The table shows that the ‘Trust’ method achieves the best results for all three tasks.
In-depth insights#
Trust Sampling#
The proposed method, Trust Sampling, offers a novel approach to constrained diffusion by framing each diffusion timestep as an independent optimization problem. Instead of alternating between diffusion steps and gradient steps on a loss function, it iteratively takes gradient steps until the proxy constraint function’s reliability is deemed low. This is determined by the variance of the sample at each diffusion level, thereby balancing fidelity to the unconditional diffusion model and adherence to the constraints. A key innovation is the introduction of trust schedules to control the number of gradient steps, preventing over-optimization of the proxy, and the estimation of the diffusion model’s state manifold to allow for early termination if the sample wanders too far. These combined mechanisms yield improved generation quality and constraint satisfaction compared to existing methods, across diverse image and motion generation tasks.
Guided Diffusion#
Guided diffusion methods enhance the capabilities of diffusion models by incorporating guidance signals during the sampling process. This allows the generation of samples that adhere to specific constraints, moving beyond unconditional generation. Classifier guidance and classifier-free guidance are prominent approaches, utilizing pre-trained classifiers or score functions to direct the sampling trajectory. However, these methods often necessitate retraining for new constraints. Loss-guided diffusion offers a more flexible alternative, using the gradient of a loss function to steer the generation. Trust sampling, as introduced in the research paper, builds upon this by formulating the inference process as a series of constrained optimization problems, enabling more accurate and controlled generation. The key improvements of trust sampling lie in its use of iterative optimization and its ability to trust the proxy constraint function judiciously, leading to higher quality outputs while addressing limitations of previous methods. Early termination strategies, based on estimating the state manifold, further enhance efficiency and sample quality.
Optimization Views#
From an optimization perspective, the paper reformulates the constrained guided diffusion process as a series of constrained optimization problems. Each optimization step involves iteratively refining the sample by following the gradient of a proxy constraint function until the proxy is deemed unreliable, based on variance analysis at each diffusion level. Trust Sampling is the core methodology, balancing the unconditional diffusion model with constraint adherence by adaptively determining the number of gradient descent steps. Early termination is also incorporated using estimated state manifold boundaries to prevent the sample from straying too far from realistic regions. This optimization framework is flexible, enabling the application of diverse constraints across different data modalities without requiring retraining of the diffusion model. The flexible optimization approach of Trust Sampling offers several advantages over prior work by allowing adaptive adjustment to the optimization process at each step, thus improving generation quality and efficiency. This iterative refinement is crucial in managing the trade-off between following the unconditional distribution and satisfying constraints, leading to superior results compared to single-step approaches.
Manifold Boundaries#
The concept of ‘manifold boundaries’ in the context of diffusion models is crucial for understanding and improving the quality of constrained generation. Manifolds represent the space of likely data points that a model has seen during training. Constrained diffusion aims to generate samples that satisfy specific conditions while remaining within this manifold. The boundaries of this manifold are important because they define the limits of trustworthy constraint optimization. When a sample strays too far from the manifold, the proxy constraint function used for guidance becomes less reliable, potentially resulting in unrealistic or nonsensical generations. Early termination mechanisms based on estimating the distance from the manifold boundary are important for efficiency as it helps prevent the model from wasting time and computation on unreliable optimization steps. Estimating these boundaries effectively involves analyzing the predicted noise magnitudes of generated samples. Samples within the boundaries exhibit noise magnitudes consistent with the model’s training data; samples outside these boundaries show noise levels that differ significantly, indicating unreliability and justifying early termination. The practical application of this principle results in more efficient and higher-quality constrained generations.
Future Directions#
Future research could explore more sophisticated trust models, perhaps incorporating uncertainty estimates or Bayesian approaches for more robust proxy guidance. Adaptive trust schedules that dynamically adjust to the complexity of the constraint and the diffusion process itself would improve efficiency. Furthermore, investigating alternative optimization methods beyond gradient descent, such as those leveraging second-order information or exploring the manifold structure of the diffusion model, could lead to more accurate and stable constrained generation. Combining trust sampling with other techniques, such as classifier guidance or score matching, warrants attention to see if synergistic improvements are possible. Finally, expanding the scope of applications, especially in complex, high-dimensional domains like 3D modeling and video generation, will be crucial in testing the generalizability and limitations of the framework. Careful consideration of potential ethical concerns, such as the generation of realistic deepfakes, is necessary for responsible development and deployment of the presented approach.
More visual insights#
More on figures

This figure shows qualitative results of different methods on solving linear inverse problems such as box inpainting and super-resolution. The left side displays results for box inpainting, where a square region of the image is masked out and the model attempts to fill it in realistically. The right side presents super-resolution results, demonstrating the ability of the models to upscale lower-resolution images. Each column represents a different method: Measurement (the input), DPS, DPS+DSG, LGD-MC, Trust (the proposed method), and Ground Truth. The figure visually compares the outputs of each method for several different image examples.

This figure shows qualitative results for two linear inverse problems: box inpainting and super-resolution. The left side displays examples of images where a square region has been masked out (box inpainting). The right side demonstrates the super-resolution of low-resolution images. For each problem, the results are shown for several different methods: DPS, DPS+DSG, LGD-MC, and Trust Sampling (the authors’ method). The figure visually compares the performance of these different methods in terms of image quality and fidelity to the original image.

This figure shows qualitative results of applying the Trust Sampling method on super-resolution tasks. The top two rows are results from the FFHQ dataset, while the bottom two rows are from ImageNet. Each row shows an example of an image with different levels of super-resolution performed using the method. The goal is to improve upon prior methods by better adhering to the original image and recovering details.

This figure shows qualitative results for the Trust Sampling method on the super-resolution task. The top two rows display results using images from the FFHQ dataset, while the bottom two rows show results from the ImageNet dataset. The figure visually demonstrates the method’s ability to improve the resolution of images while preserving image details and overall quality.

This figure shows the qualitative results of applying the Trust Sampling method to various human motion generation tasks. Each row represents a different task, including hand and foot tracking, jumping, root tracking, and obstacle avoidance. The tasks involve generating motions that adhere to specific constraints. For example, the ‘jumping’ task requires the generated motion to clear a certain height, indicated by the horizontal dotted line. The visualization highlights the method’s ability to effectively balance between adhering to the constraints and maintaining the natural appearance of the generated motion.
More on tables
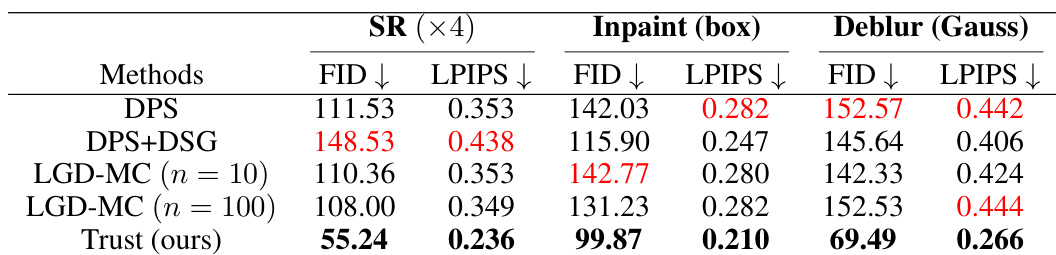
This table presents a quantitative comparison of different methods for solving three linear inverse problems (Super-Resolution, Inpainting, and Deblurring) on the ImageNet dataset. The performance of each method is measured using two metrics: Fréchet Inception Distance (FID) and Learned Perceptual Image Patch Similarity (LPIPS). Lower FID and LPIPS scores indicate better performance. The table highlights the best-performing method for each task in bold and the worst-performing method in red.
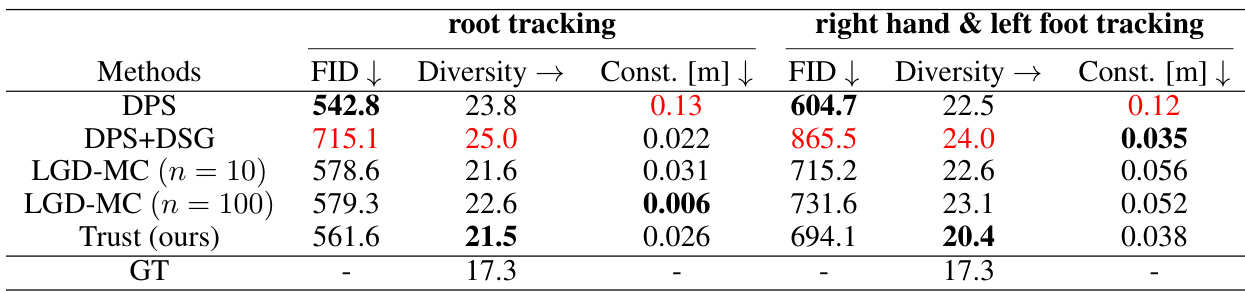
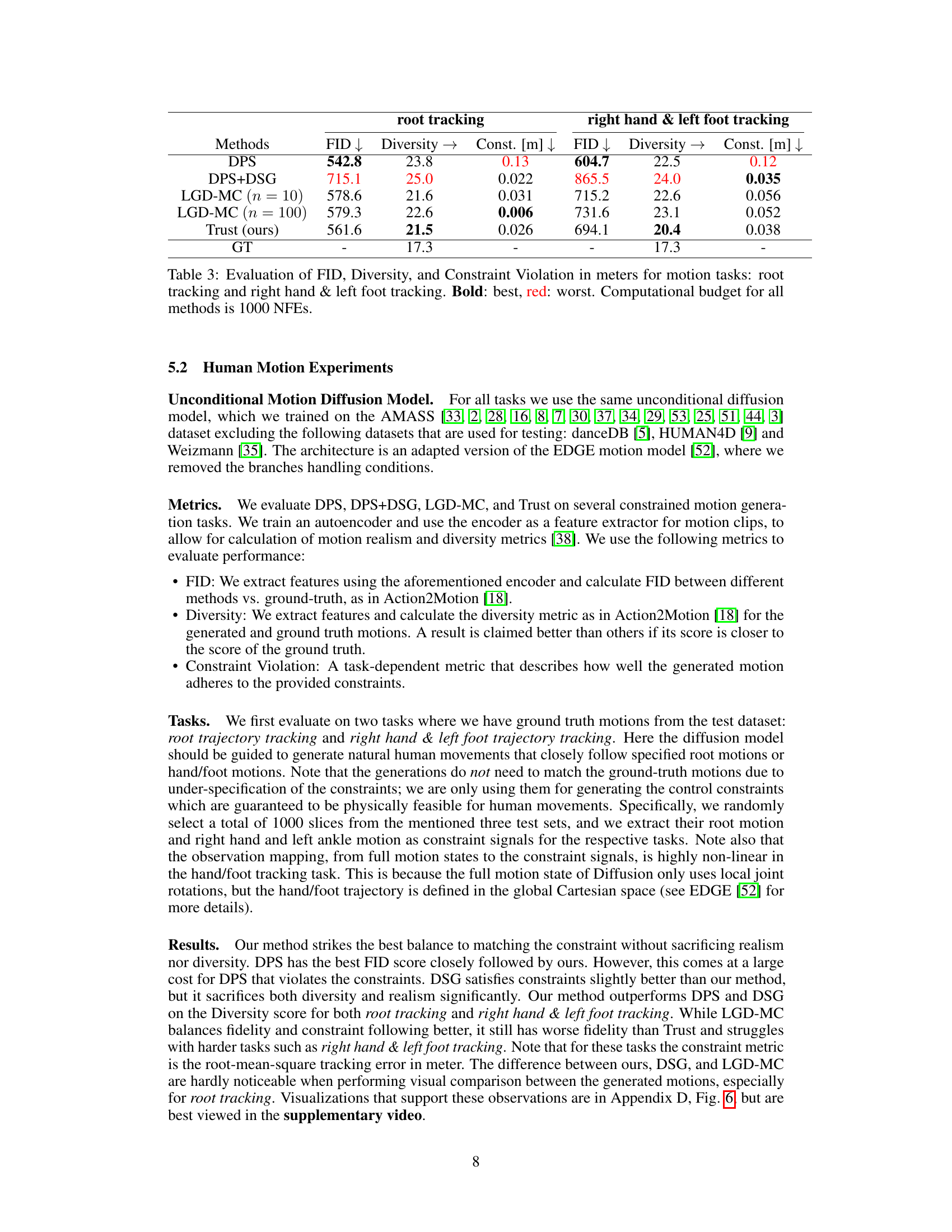
This table presents a quantitative comparison of different methods (DPS, DPS+DSG, LGD-MC, and Trust Sampling) on two human motion generation tasks: root tracking and right hand & left foot tracking. The evaluation metrics include FID (Fréchet Inception Distance), which measures the quality of generated motion; Diversity, indicating the variety of generated motion sequences; and Constraint Violation (in meters), representing how well the generated motion adheres to the specified constraints. The results show that Trust Sampling achieves a good balance between FID, Diversity, and constraint satisfaction.
This table presents the quantitative results of three different image restoration tasks (Super-Resolution, Inpainting, Deblurring) evaluated using two metrics: Fréchet Inception Distance (FID) and Learned Perceptual Image Patch Similarity (LPIPS). The results are shown for four methods: DPS, DPS+DSG, LGD-MC (with 10 and 100 samples), and Trust Sampling (the proposed method). Lower FID and LPIPS scores indicate better performance. The experiments were conducted on 1000 validation images from the FFHQ dataset (256x256 resolution).

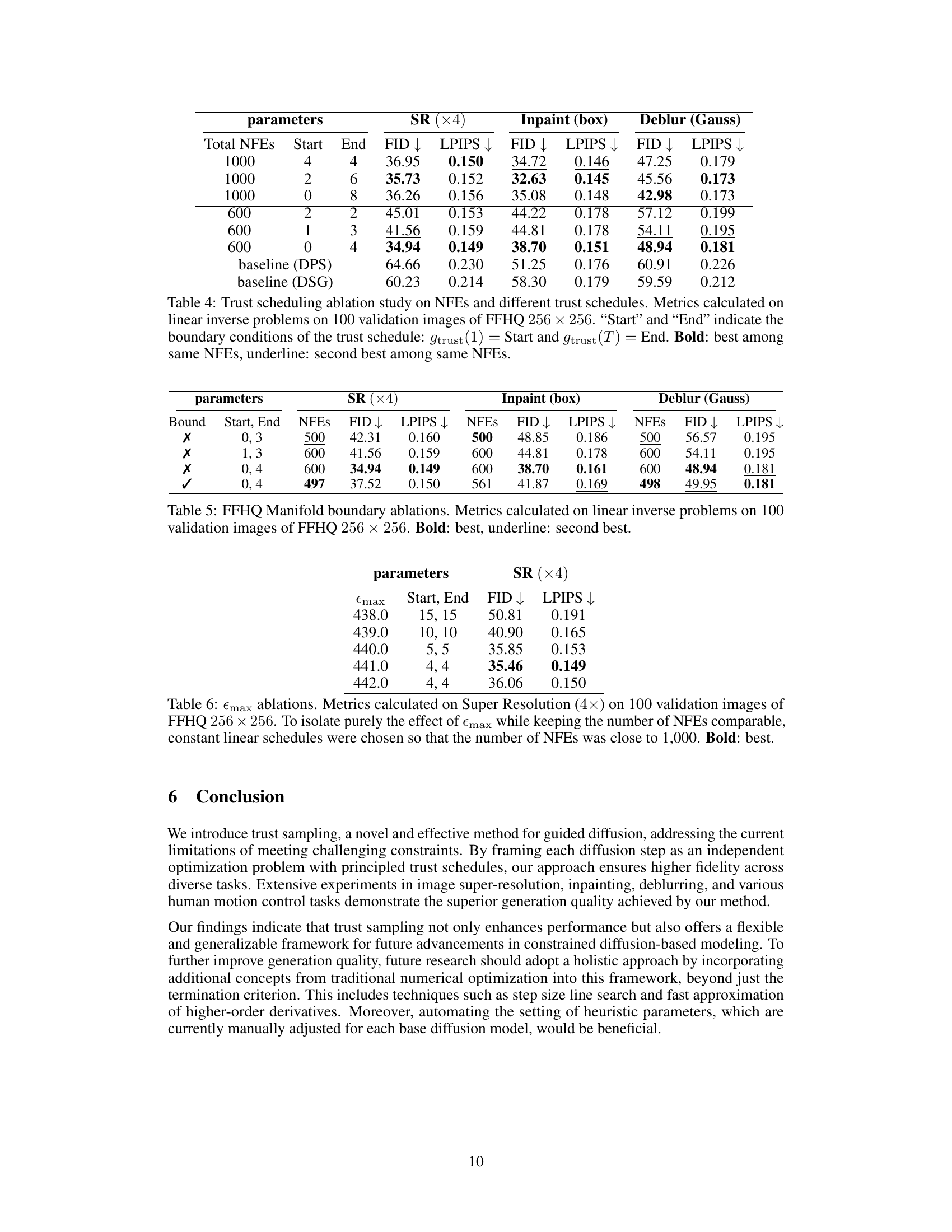
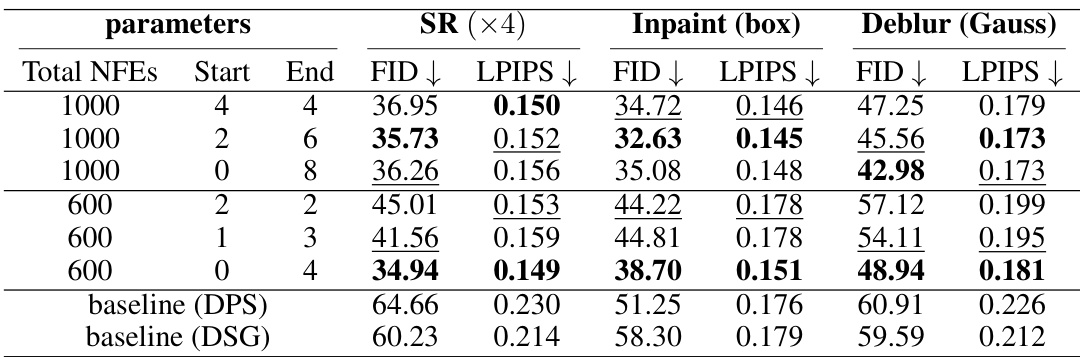
This table presents ablation study results on the impact of using manifold boundary estimates in the Trust Sampling algorithm. It compares different trust schedule parameters (‘Start’, ‘End’) and total number of function evaluations (NFEs) across three image restoration tasks (Super-Resolution, Inpainting, Deblurring) using the FFHQ dataset. The results show the effect of incorporating manifold boundary estimates on model performance, measured by FID and LPIPS scores. The best performing configurations are highlighted.
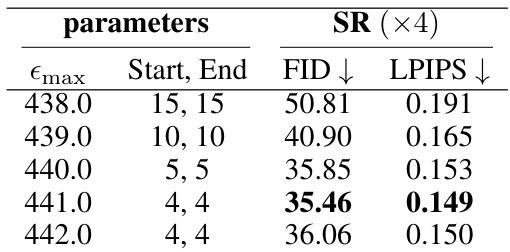
This table presents ablation results on the effect of varying the parameter Emax on the super-resolution task using the FFHQ dataset. Different values of Emax were tested, each with a corresponding constant linear trust schedule designed to keep the number of neural function evaluations (NFEs) around 1000. The results show the FID and LPIPS scores obtained for each Emax value, with the best performing Emax value highlighted in bold.

This table lists the hyperparameters used in the image experiments. For each task (Super-Resolution, Inpainting, Deblurring) on each dataset (FFHQ, ImageNet), it shows the maximum number of neural function evaluations (NFEs), the number of DDIM steps, the starting and ending points of the stochastic linear trust schedule used for termination criteria, and the maximum allowed predicted noise magnitude (εmax). The table separates the results based on whether 1000 or 600 NFEs were used.
Full paper#