↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current neural image compression methods typically use simple scalar quantization for the latent representations, which limits performance. While vector quantization offers better performance, it’s computationally expensive. This paper tackles this challenge.
The proposed solution is a novel learning method that designs optimal lattice vector quantizers (OLVQ). OLVQ learns the optimal codebooks based on the statistics of latent features, achieving better rate-distortion performance than traditional methods. This method is efficient and improves image compression significantly, while retaining the computational efficiency of scalar quantization.
Key Takeaways#
Why does it matter?#
This paper is important because it significantly improves the rate-distortion performance of neural image compression by learning optimal lattice vector quantizers. This addresses a critical limitation of current methods and opens new avenues for research in efficient and high-quality image compression techniques. The proposed approach is computationally efficient, making it suitable for various applications, including resource-constrained devices. The findings have broader implications for various fields that rely heavily on image data.
Visual Insights#

This figure compares three different types of quantizers: uniform scalar quantizer (USQ), lattice vector quantizer (LVQ), and general vector quantizer (GVQ) in two dimensions. It visually demonstrates how codewords (points) are organized and partitioned in each method. The USQ uses uniformly spaced horizontal and vertical lines, LVQ uses a structured hexagonal lattice, and GVQ allows for arbitrarily shaped Voronoi cells to optimally fit the data distribution. This illustrates the trade-off between complexity and effectiveness.
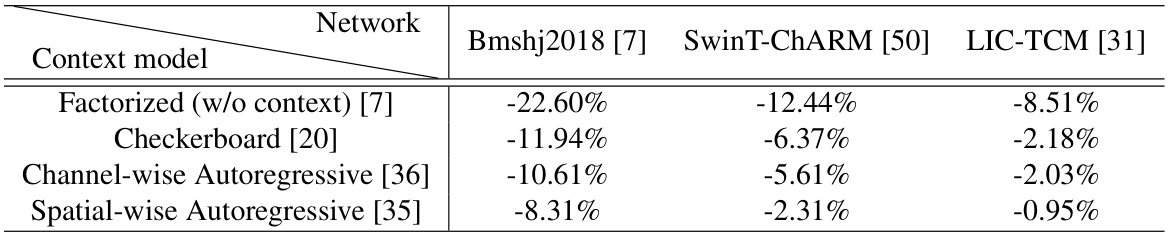
This table presents the bitrate savings achieved by using the Optimal Lattice Vector Quantization (OLVQ) method compared to a standard scalar quantizer. The results are shown for three different image compression networks (Bmshj2018, SwinT-ChARM, LIC-TCM) and four different context models (Factorized, Checkerboard, Channel-wise Autoregressive, Spatial-wise Autoregressive). A negative percentage indicates bitrate savings, showing the improvement achieved by OLVQ over the scalar quantizer. The lattice vector dimension was set to 32 for all results shown.
In-depth insights#
Optimal LVQ Design#
Optimal Lattice Vector Quantization (LVQ) design hinges on overcoming the limitations of traditional LVQ’s which are often optimized for uniform data distributions, making them suboptimal for real-world, complex data like image latent features. A key challenge is adapting the LVQ structure to the specific characteristics of the data distribution. This necessitates a move beyond fixed lattice structures to a learning-based approach. Learning the optimal lattice codebook involves finding the basis vectors that best shape and orient the quantizer cells to minimize distortion and coding rate. This can be achieved through end-to-end training, which directly optimizes for rate-distortion performance. The learning process should be carefully designed to handle the non-differentiability of the traditional closest vector problem, which is commonly addressed using techniques like Babai’s rounding method. Furthermore, constraints such as orthogonality on basis vectors can significantly enhance the accuracy of quantization and improve training stability. Overall, an optimal LVQ design involves a delicate balance between learning flexibility, computational efficiency, and the inherent structural constraints of lattices, necessitating innovative learning methods.
DNN Compression#
Deep Neural Network (DNN) compression techniques aim to reduce the size and computational cost of DNNs without significant performance degradation. Model compression strategies encompass various methods, such as pruning, quantization, knowledge distillation, and low-rank approximation. Pruning removes less important connections or neurons, while quantization reduces the precision of weights and activations. Knowledge distillation transfers knowledge from a larger, more complex model to a smaller one. Low-rank approximation decomposes weight matrices into lower-rank representations. The choice of method often depends on the specific DNN architecture, target platform, and acceptable accuracy loss. Optimizing for both storage and speed is crucial, as compressed models ideally should be faster and require less memory. The effectiveness of each technique often varies depending on factors such as the dataset and model architecture. Research continues to explore novel hybrid methods and improvements to existing ones to further enhance compression ratios and maintain accuracy.
Rate-Distortion#
Rate-distortion theory is fundamental to lossy data compression, aiming to minimize distortion for a given rate (or vice versa). In the context of neural image compression, rate refers to the number of bits used to represent the compressed image, while distortion measures the difference between the original and reconstructed images, often using metrics like PSNR or MS-SSIM. The optimal rate-distortion performance is achieved by balancing these competing factors. The paper explores this balance by proposing a novel learning method for optimal lattice vector quantization (OLVQ), showing improvements in rate-distortion performance compared to traditional scalar quantization techniques. The key is the adaptive nature of OLVQ, which learns to fit the quantizer structure to the specific distribution of the latent features, leading to better compression efficiency. The experimental results demonstrate significant bitrate savings while maintaining good image quality, highlighting the effectiveness of the proposed approach in optimizing the trade-off between rate and distortion.
Orthogonal LVQ#
Orthogonal Lattice Vector Quantization (LVQ) presents a compelling approach to neural image compression by leveraging the structured nature of lattices while addressing the limitations of traditional LVQ methods. Standard LVQ methods, optimized for uniform data distributions, often underperform with the complex, non-uniform distributions encountered in latent spaces of deep neural networks. Orthogonal LVQ improves upon this by imposing orthogonality constraints on the basis vectors of the lattice generator matrix. This constraint enhances the accuracy of the quantization process, particularly when using Babai’s rounding technique for efficient nearest-neighbor search. The key advantage is the improved balance between computational efficiency and compression performance. By better aligning the quantizer cells with the underlying data distribution, orthogonal LVQ facilitates a more effective exploitation of inter-feature dependencies, ultimately leading to superior rate-distortion results. This approach moves beyond the limitations of uniform scalar quantization and traditional LVQ, offering a potentially significant advancement in end-to-end neural image compression systems. The effectiveness of this approach would be further strengthened by rigorous evaluation of its robustness under various image complexities, network architectures, and training procedures, alongside a thorough comparison with other sophisticated quantization techniques. Further investigations into the optimal dimensionality and lattice structure would further refine the method’s capabilities and expand its potential applications in broader image compression research.
Future of LVQ#
The future of Lattice Vector Quantization (LVQ) appears bright, particularly within the context of neural image compression. LVQ’s inherent structural efficiency provides a compelling advantage over unstructured vector quantization methods, while offering a computational cost closer to scalar quantization. Future research could focus on adaptive LVQ techniques that dynamically adjust lattice parameters based on data characteristics, moving beyond the currently explored rate-distortion optimized (OLVQ) approach. This might involve incorporating learned metrics of data complexity to automatically determine optimal lattice structures. Furthermore, exploring the use of novel lattice structures beyond traditional ones could yield significant performance improvements. Finally, integrating LVQ with advancements in deep learning architectures such as transformers, and investigating its application in other domains beyond image compression (e.g., audio or video compression, feature extraction) are promising avenues for further development and wider adoption of this effective quantization method.
More visual insights#
More on tables
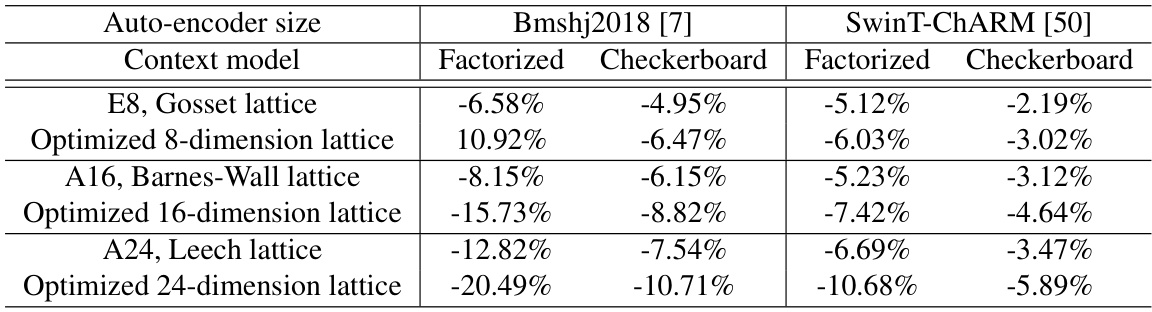
This table presents a comparison of bitrate savings achieved by various lattice vector quantization methods against a scalar quantizer. It shows the performance of classical, pre-defined lattices (Gosset, Barnes-Wall, Leech) and the learned, optimized lattices of the proposed method. Results are broken down by autoencoder size (Bmshj2018, SwinT-CHARM), and context model (Factorized, Checkerboard). The optimized lattices consistently outperform both the scalar quantizer and the pre-defined lattices, demonstrating the effectiveness of the proposed learning approach in adapting to specific data distributions.
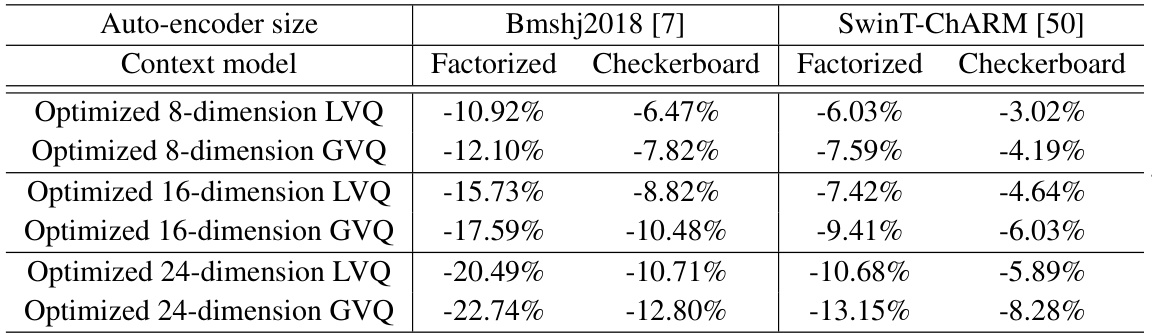
This table compares the bitrate savings achieved by using different types of lattice vector quantization methods (classical pre-defined and learned optimal) against the scalar quantizer. The comparison is done across various image compression models (Bmshj2018 and SwinT-ChARM) and context models (Factorized and Checkerboard). The table shows how much better the learned optimal lattice vector quantizers perform in terms of bitrate savings compared to the other methods.

This table compares the inference times of three different quantization methods: uniform scalar quantization (USQ), lattice vector quantization (LVQ), and general vector quantization (GVQ) across different dimensions (1, 8, 16, and 32). For the general vector quantizer, the codebook size was increased as the dimension increased. The table shows that USQ has the fastest inference time, followed by LVQ, and then GVQ, highlighting LVQ’s balance between computational efficiency and scalability.

This table presents the bitrate savings achieved by the proposed optimal lattice vector quantization (OLVQ) method compared to a standard scalar quantizer across various image compression network models and context models. The results are presented as percentages of bitrate reduction. The lattice vector dimension used in these experiments is 32.

This table compares the bitrate savings achieved by using different lattice vector quantization methods against a scalar quantizer in image compression. It shows results for both pre-defined (classical) lattices (Gosset, Barnes-Wall, Leech) and the learned optimal lattices, across two different compression network models (Bmshj2018 and SwinT-CHARM) and two context models (Factorized and Checkerboard). The table highlights how the proposed learned optimal lattice quantizer significantly outperforms both the scalar quantizer and the pre-defined lattices.
Full paper#



















