↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current quantized/binarized training approaches for deep learning suffer from performance loss and high computational costs due to approximations of gradients. This paper addresses these issues by proposing a novel mathematical principle: Boolean variation, a new calculus for Boolean logic. This allows training deep learning models directly with Boolean weights and/or activations.
The proposed Boolean Logic Deep Learning (BOLD) framework introduces Boolean backpropagation and optimization, enabling native Boolean domain training. Extensive experiments show that BOLD achieves baseline full-precision accuracy in ImageNet classification and surpasses state-of-the-art in other tasks (semantic segmentation, super-resolution, NLP), while significantly reducing energy consumption. BOLD provides a scalable and efficient algorithm for natively training deep models in binary, addressing a major open challenge in the field.
Key Takeaways#
Why does it matter?#
This paper is highly important for researchers as it presents a novel framework for training deep learning models natively in the Boolean domain, significantly reducing energy consumption and computational costs while achieving state-of-the-art accuracy in various tasks. It opens new avenues for research in low-precision arithmetic design and hardware acceleration of deep learning models, particularly in resource-constrained environments such as edge devices. The framework’s generality and flexibility make it applicable to various network architectures, potentially leading to more efficient and sustainable AI systems.
Visual Insights#
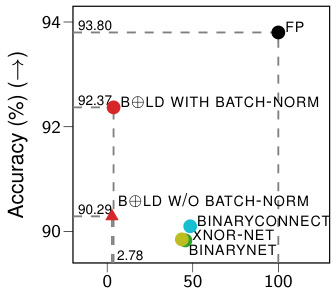
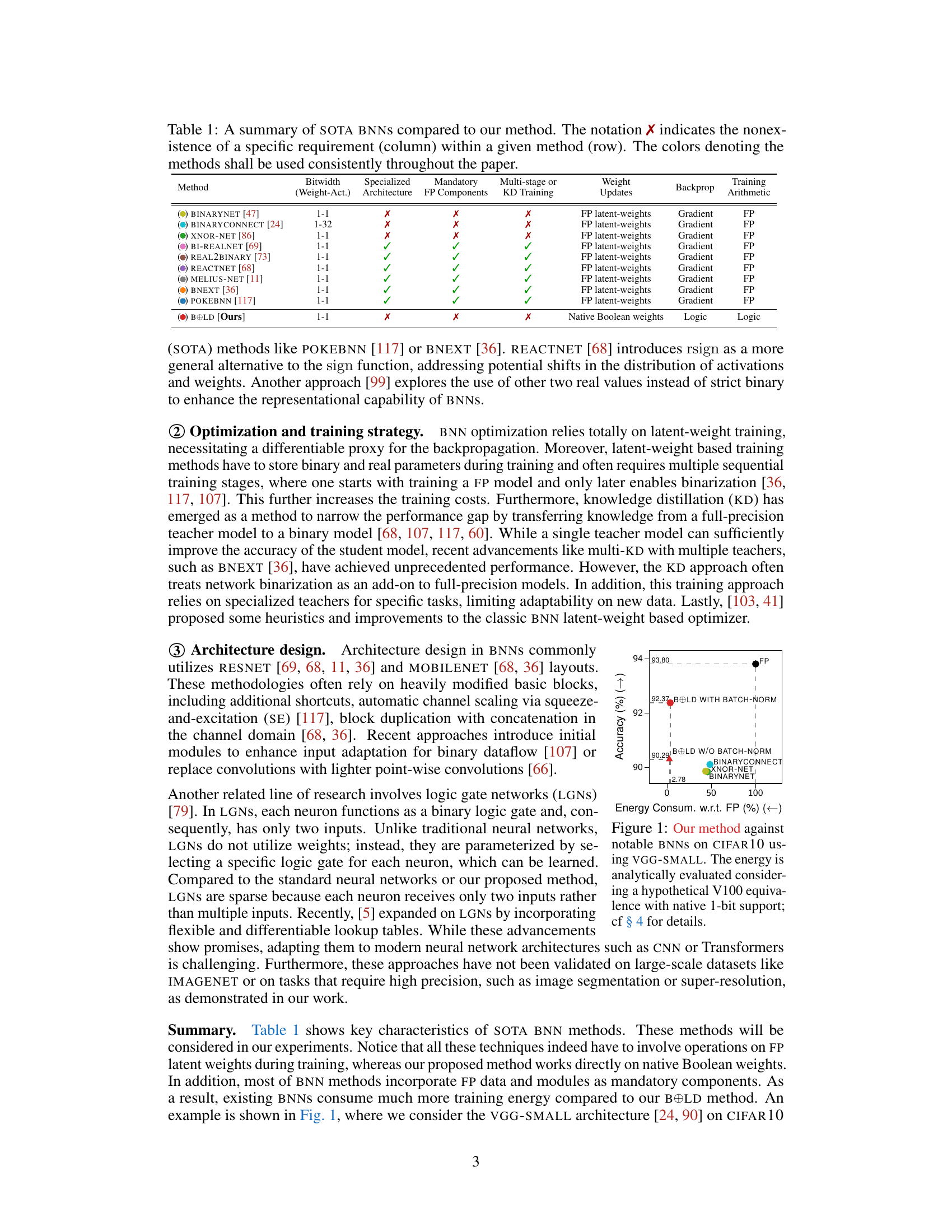
The figure compares the performance of the proposed BOLD method against other state-of-the-art binarized neural networks (BNNs) on the CIFAR10 dataset using the VGG-SMALL architecture. It shows that BOLD achieves comparable accuracy while significantly reducing energy consumption during both training and inference, demonstrating its superior efficiency compared to existing BNN methods. The energy consumption is calculated analytically based on the hypothetical V100 architecture with native 1-bit support, with further details provided in section 4 of the paper.
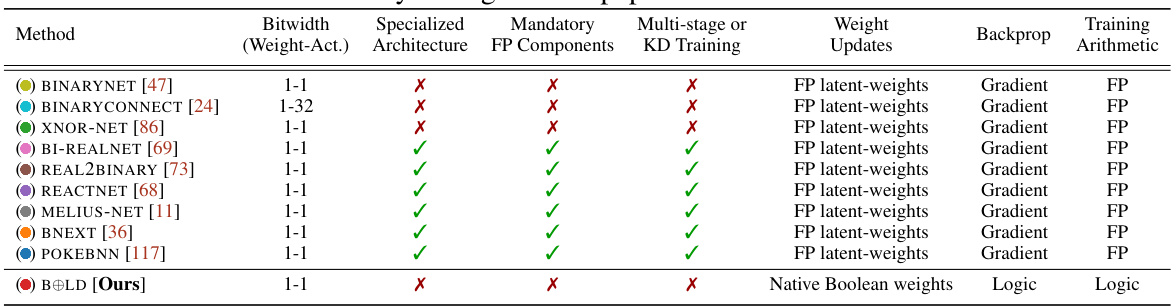
This table compares the state-of-the-art (SOTA) binarized neural networks (BNNs) with the proposed method BOLD. It highlights key characteristics of each method, including the bitwidth of weights and activations, whether the method uses a specialized architecture, if full-precision components are mandatory, whether multi-stage training or knowledge distillation (KD) is employed, the type of weight updates, the backpropagation method used, and the arithmetic used in training. The table helps illustrate how BOLD differs from existing approaches by natively training Boolean weights and activations without relying on full-precision latent weights, thereby achieving significant efficiency gains.
In-depth insights#
Boolean Logic NN#
Boolean Logic Neural Networks represent a novel approach to neural network design, moving beyond the typical reliance on real-valued arithmetic. By employing Boolean logic operations for weight updates and neuron activations, BOLD significantly reduces computational complexity and energy consumption. This is achieved by training the network natively in the Boolean domain, eliminating the need for computationally expensive gradient approximations inherent in traditional binarized neural networks. While this paradigm shift leads to notable performance gains in various applications, it also presents challenges. The convergence properties of Boolean Logic NNs require careful analysis, and further research is needed to determine the limits of their expressiveness in approximating complex functions and to explore hardware implementations which may be needed for widespread applicability. The theoretical foundation for BOLD, including the novel concept of Boolean variation and its associated chain rule, establishes a rigorous mathematical framework for this new approach to neural network training. Early empirical results show significant energy and computational savings with comparable or even improved performance on certain tasks. Further research into hardware acceleration and the development of more sophisticated optimization strategies will be critical to fully realize the potential of Boolean Logic NNs.
BOLD Training#
The concept of “BOLD Training” introduces a novel approach to training deep neural networks, focusing on leveraging Boolean logic operations for enhanced efficiency. Instead of relying on traditional real-valued arithmetic, BOLD uses Boolean representations for both weights and activations. This allows for drastically reduced memory usage and potentially lower energy consumption during training. The key innovation lies in its novel mathematical framework, which defines a notion of Boolean variation that enables the use of backpropagation in the Boolean domain. The framework allows for the training of Boolean weights directly without the need for approximate gradient calculations or the maintenance of high-precision latent weights, which are common limitations of existing binary neural network approaches. Theoretical analysis, supporting the convergence of the method, is presented, while the practical efficacy is demonstrated across a range of challenging tasks including image classification, super-resolution and natural language processing. Experimental results highlight significant performance improvements and substantial efficiency gains compared to state-of-the-art binary neural networks.
ImageNet Results#
An ImageNet analysis would be crucial for evaluating the proposed Boolean Logic Deep Learning (BOLD) method. It would involve comparing BOLD’s performance against existing state-of-the-art (SOTA) models on ImageNet classification. Key metrics to consider are top-1 and top-5 accuracy, which measure the model’s ability to correctly classify images. Additionally, energy efficiency during both training and inference phases should be analyzed as a primary focus. The results should showcase BOLD’s ability to achieve SOTA accuracy while significantly reducing energy consumption. Detailed analysis would look into the effect of various model designs and architectural choices on accuracy and efficiency. A comparison with different quantization techniques is needed, and it is expected that BOLD would demonstrate a clear superiority in terms of energy efficiency while being competitive in terms of accuracy. The analysis should extend to an evaluation of training speed, showing faster convergence compared to existing binarized neural networks (BNNs). Finally, a discussion on the scalability and limitations of BOLD in the context of ImageNet would provide valuable insights into its potential applicability for real-world large-scale applications.
Energy Efficiency#
The research paper significantly emphasizes energy efficiency as a crucial factor in evaluating deep learning model performance, contrasting it with traditional metrics like FLOPS. It argues that existing binarized neural network (BNN) approaches, while aiming to reduce computational complexity, often fall short due to reliance on full-precision latent weights and approximations during training. The proposed Boolean Logic Deep Learning (BOLD) framework directly addresses this by natively operating in the Boolean domain, thereby achieving substantial energy savings during both training and inference. The authors back up their claims through analytical evaluations and extensive experiments on various tasks. They demonstrate that BOLD achieves comparable or even surpassing accuracy compared to the state-of-the-art BNNS, while significantly reducing energy consumption across various datasets and model architectures. The analytical evaluation of energy consumption considers chip architecture, memory hierarchy, data flow, and arithmetic precision, illustrating a comprehensive approach to measuring efficiency that moves beyond simple operational count estimations. This focus on practical efficiency makes the BOLD framework a promising development for resource-constrained environments and edge computing applications.
Future of BOLD#
The future of Boolean Logic Deep Learning (BOLD) is bright, promising significant advancements in deep learning. BOLD’s inherent efficiency, stemming from its native Boolean operations, positions it as a leading candidate for resource-constrained environments like edge computing and mobile devices. Further research could explore BOLD’s compatibility with diverse network architectures, extending beyond CNNs and transformers to encompass other model types. Improving the training algorithms to further enhance convergence speed and stability while maintaining accuracy is crucial. The development of specialized hardware tailored to BOLD’s unique computational characteristics could unlock its full potential, leading to substantial performance gains. Exploring the theoretical underpinnings of BOLD through a rigorous mathematical framework will solidify its foundation. Finally, investigating BOLD’s application to novel domains such as reinforcement learning and causal inference could open up new possibilities for innovation.
More visual insights#
More on figures

This figure illustrates the backpropagation process in a network containing a Boolean linear layer. It shows how signals flow between layers. The key is that the signals (δLoss/δxl+1k,j and δLoss/δxlk,i) can be either real-valued or Boolean, depending on the nature of the subsequent (l+1) layer. The Boolean linear layer (layer l) uses Boolean weights (wli,j ∈ B) and Boolean inputs (xlk,i ∈ B) to process the data. The figure highlights that the framework is flexible to handle different layer types and data types.

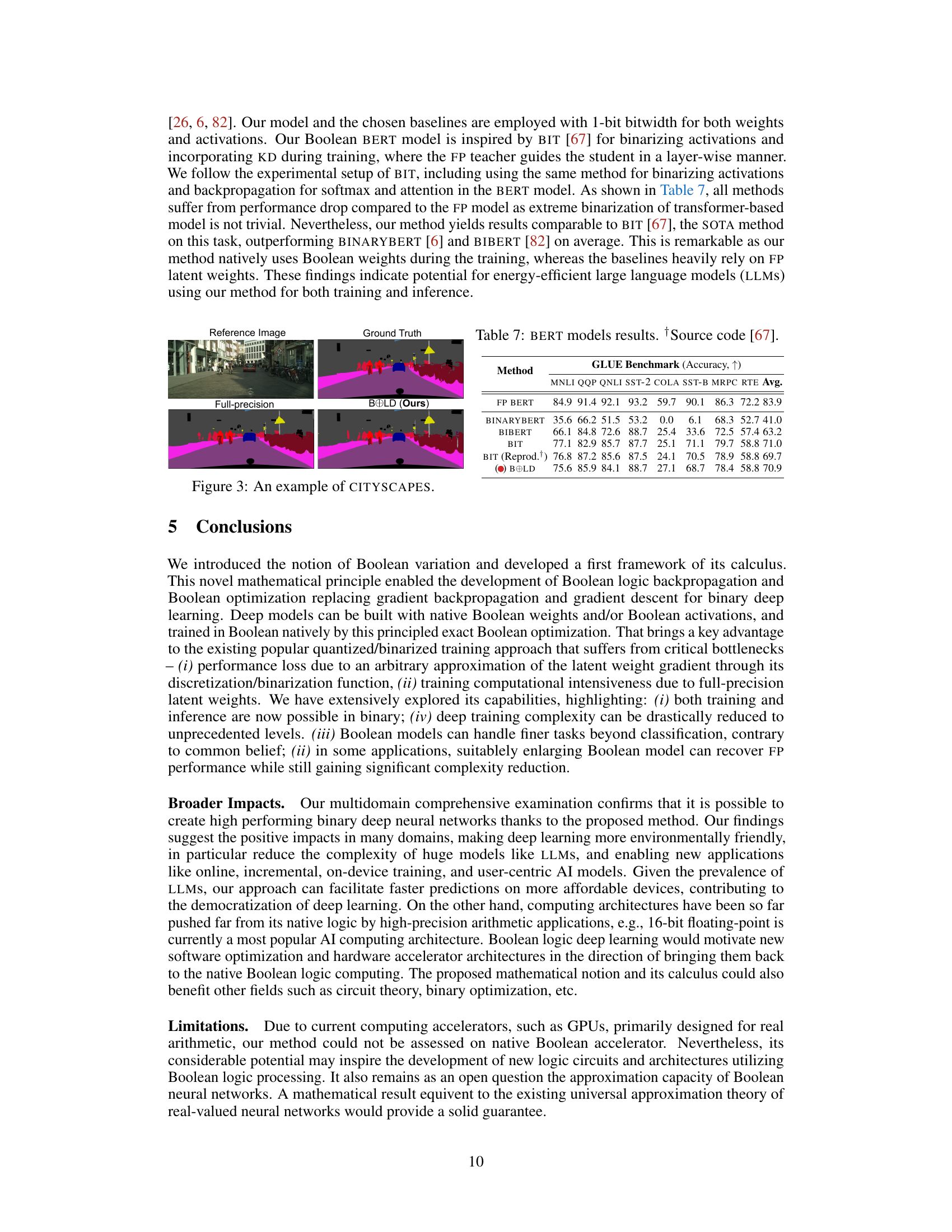
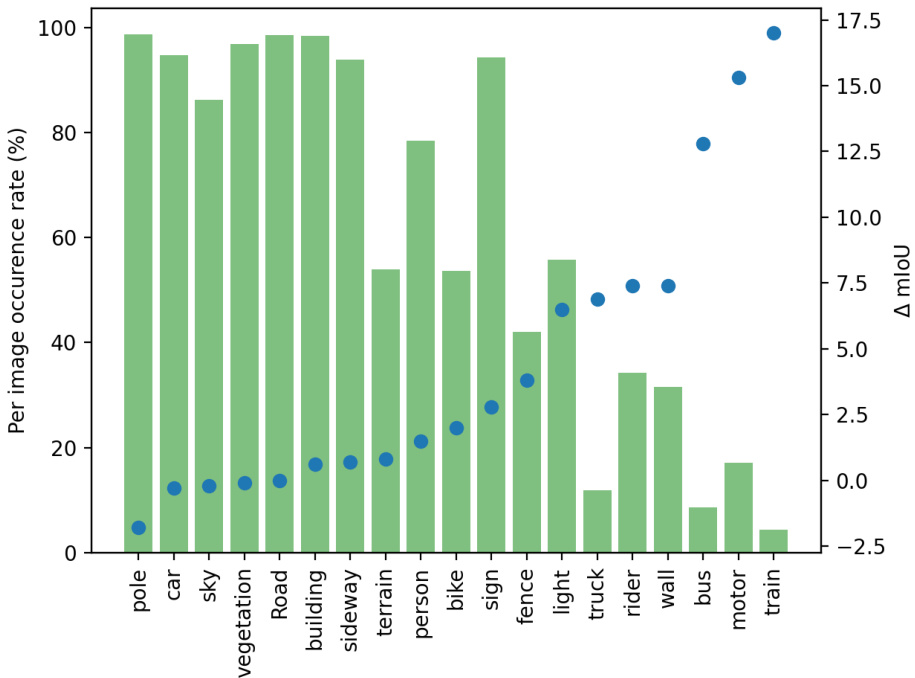
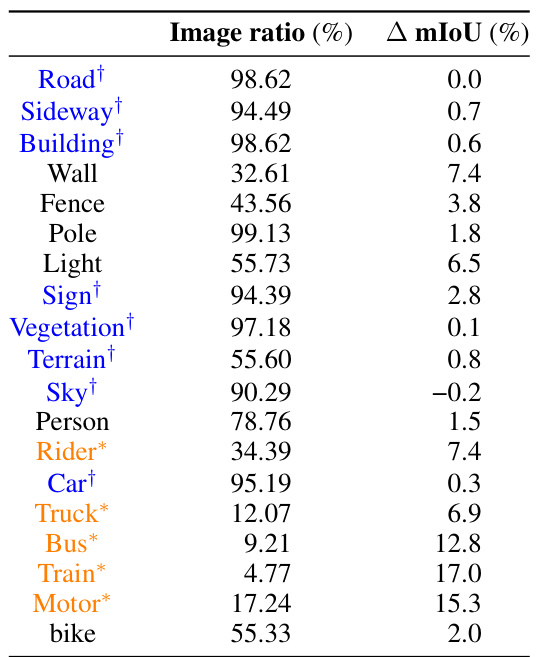
This figure shows a qualitative comparison of semantic segmentation results on the CITYSCAPES dataset. The top row displays the input image and the ground truth segmentation mask. The bottom row shows the segmentation results from a full-precision model and the BOLD (Boolean Logic Deep Learning) model. The colors in the segmentation masks represent different classes in the CITYSCAPES dataset (e.g., road, building, person, vehicle). The figure is intended to visually demonstrate the performance of the BOLD model compared to a full-precision baseline model. Note that, although the BOLD model uses significantly less precision, the qualitative results seem very close to the results from the full-precision model.
This figure compares the performance of the proposed BOLD method against other state-of-the-art binarized neural networks (BNNs) on the CIFAR-10 dataset using the VGG-Small architecture. It highlights the significant energy savings achieved by BOLD while maintaining competitive accuracy. The energy consumption is analytically estimated, considering the hypothetical use of a V100 GPU with native 1-bit support. Further details are provided in Section 4 of the paper.

This figure compares the performance of the proposed BOLD method against other state-of-the-art binarized neural networks (BNNs) on the CIFAR-10 dataset using the VGG-SMALL architecture. It highlights the significant reduction in energy consumption achieved by BOLD during both training and inference while maintaining comparable accuracy to other methods. The energy values are analytically estimated based on a hypothetical NVIDIA V100 GPU with native 1-bit support, and further details are available in section 4 of the paper.
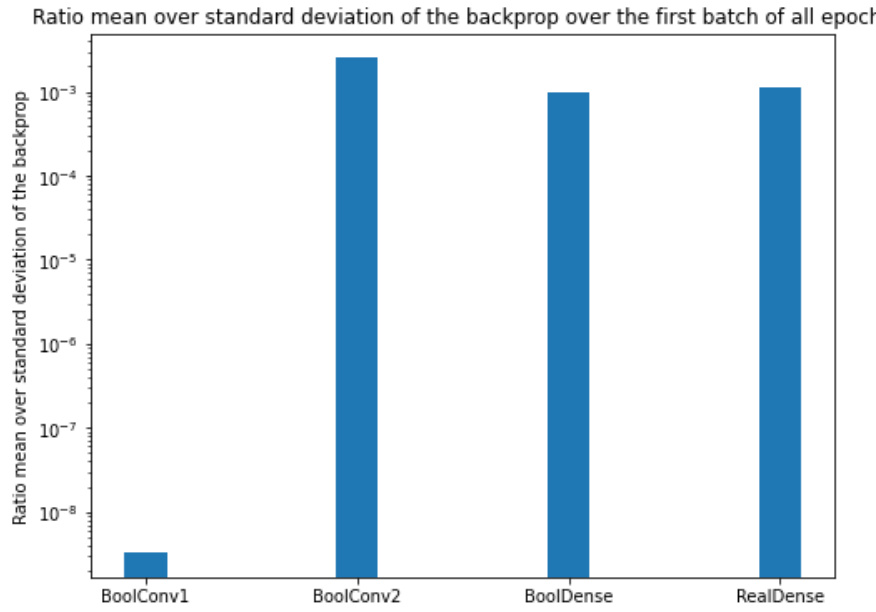
This figure shows the empirical ratio of the mean to standard deviation of the backpropagation signal. The experiment was conducted using a CNN composed of BoolConv, BoolConv, BoolDense, and RealDense layers with the MNIST dataset. The results are presented as a bar chart, showing the ratio for each layer type.
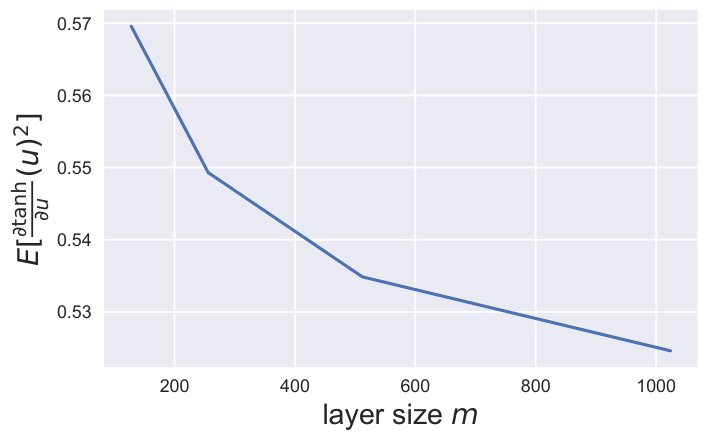
The figure shows the expected value of the derivative of the hyperbolic tangent function (tanh) with respect to its input, where the input is an integer. The plot shows how this expected value changes as the output size (m) of the layer varies. The expected value of the tanh derivative decreases as m increases, indicating a decreasing impact of the activation function’s non-linearity as the layer size grows. This observation is important for understanding the backpropagation behavior in Boolean Logic Deep Learning (BOLD), where the activation function is a threshold function and this effect is considered in the scaling of the backpropagation signals.

This figure shows two different designs for Boolean blocks in a neural network architecture. Block I is a simpler design that uses mostly Boolean operations, while Block II uses a combination of Boolean and real-valued operations. Block II also has additional shortcut and concatenation operations. The figure also shows the layout of the standard RESNET18 architecture for comparison.

This figure compares four different types of neural network blocks, including a Boolean block without batch normalization (BN), a BNEXT sub-block [36], a REACTNET [68] block, and a BINEAL-NET [77] block. It highlights that the Boolean block uses only binary operations, while the others employ a mix of binary and full-precision (FP) operations, particularly Batch Normalization, PReLU activation function, and Squeeze-and-Excitation modules. The figure emphasizes the greater efficiency and simplicity of the Boolean block due to its reduced reliance on full-precision operations. Different dataflows are also shown using arrows (binary, integer, real).
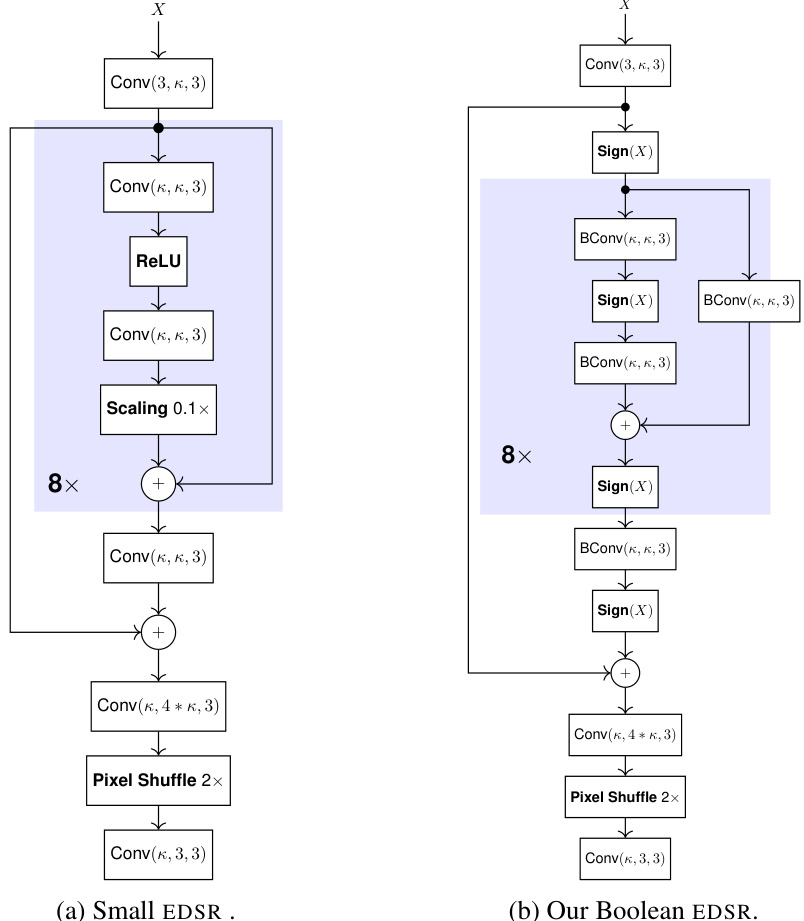
This figure compares the architecture of a standard EDSR model for super-resolution with the proposed Boolean EDSR model. The standard EDSR uses convolutional layers with ReLU activation functions, while the Boolean EDSR replaces these with Boolean convolution layers and a Boolean activation function. Both models use the same basic structure, including residual blocks and a final pixel shuffle layer, illustrating how the Boolean methods can be applied to existing network architectures.

This figure shows the results of applying the proposed Boolean super-resolution method to two images: one from the BSD100 dataset (‘013’) and one from the Set14 dataset (‘014’). The ground truth high-resolution images are shown next to their corresponding outputs from the Boolean super-resolution method. The Peak Signal-to-Noise Ratio (PSNR) values are provided as a quantitative measure of the method’s performance.

This figure compares a ground-truth high-resolution image with the output of the Boolean super-resolution model. The model is able to generate a visually similar image to the ground truth, with a PSNR of 34.90 dB. The enlarged crops allow for a detailed comparison of textures and details.
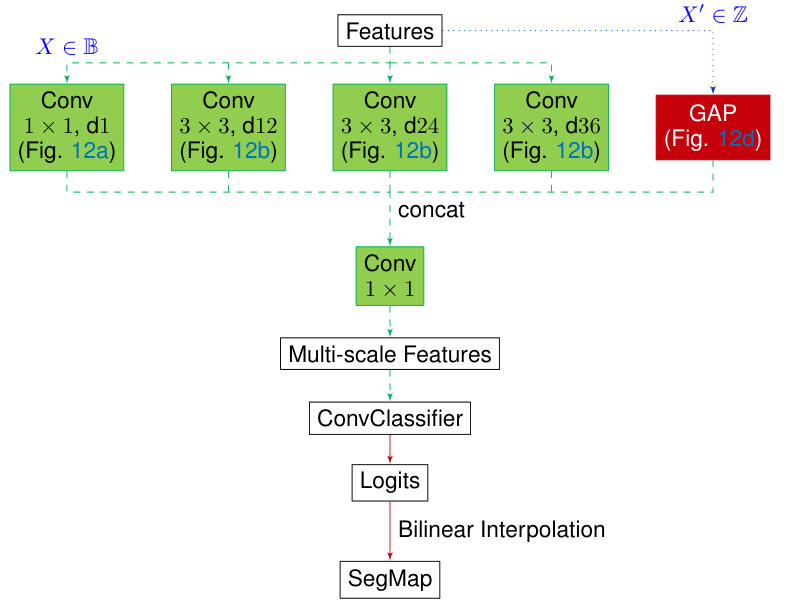
This figure illustrates the architecture of the Boolean semantic segmentation model. It shows the flow of data through different layers and operations, starting from input features and ending with the output segmentation map. The model utilizes a combination of Boolean convolutional layers, a multi-scale feature extraction block using dilated convolutions (ASPP), and a final classifier layer.
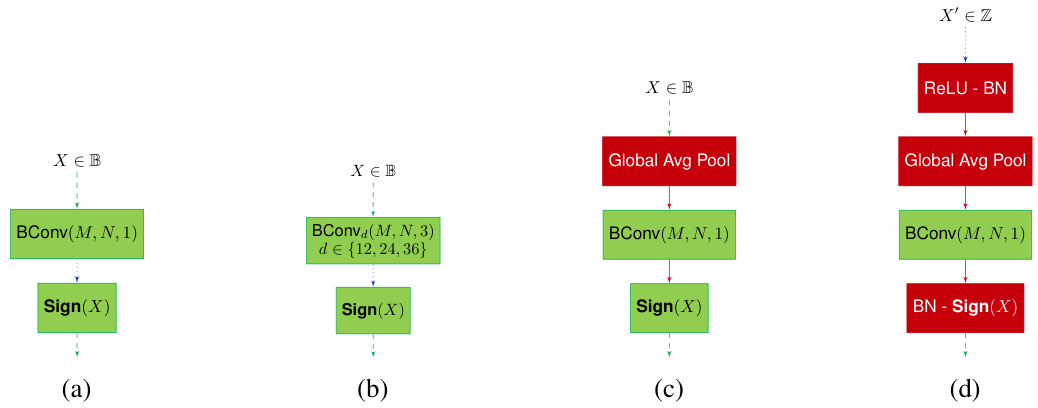
This figure shows the architecture of the Boolean Atrous Spatial Pyramid Pooling (BOOL-ASPP) module used in the semantic segmentation task. It highlights the four main branches: a 1x1 convolution branch, three 3x3 dilated convolution branches with varying dilation rates, a naive global average pooling branch, and a modified global average pooling branch. The figure illustrates how these branches process Boolean inputs (X ∈ B) and eventually produce a final output (X’ ∈ Z). The use of Boolean convolutions (BConv) and Boolean activation functions (Sign(X)) are clearly marked, showing a core aspect of the BOLD approach. The modified GAP branch emphasizes a key difference between the BOOL-ASPP and the standard ASPP, showcasing the unique handling of inputs within BOLD.
This figure compares the performance of the proposed BOLD method against other state-of-the-art binarized neural networks (BNNs) on the CIFAR-10 dataset using the VGG-SMALL architecture. The key metric shown is the energy consumption relative to the full-precision baseline. BOLD demonstrates significantly lower energy consumption while maintaining comparable accuracy.
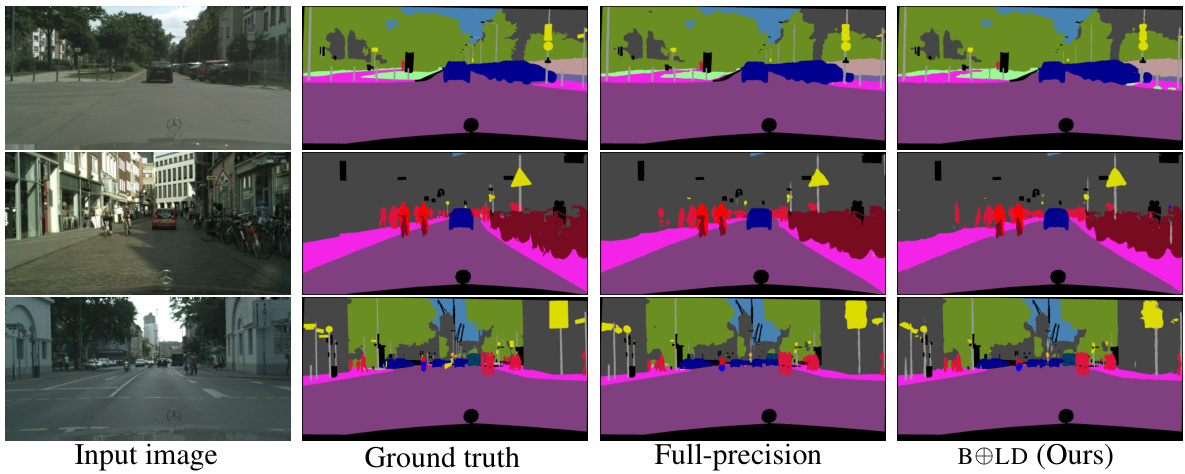
This figure shows a qualitative comparison of the results obtained using different methods on the CITYSCAPES validation set. Three image examples are shown, each with the input image, the ground truth segmentation, the segmentation produced by a full-precision model, and the segmentation result produced by the proposed BOLD (Boolean Logic Deep Learning) method. The goal is to visually demonstrate the comparable performance of the BOLD method against the full precision baseline.
More on tables

This table compares the state-of-the-art (SOTA) binarized neural networks (BNNs) with the proposed BOLD method. It highlights key differences in bitwidth, specialized architecture requirements, use of full-precision components, knowledge distillation (KD), and the nature of weight updates and backpropagation. The table helps demonstrate that BOLD offers significant advantages in terms of efficiency and adaptability compared to existing BNN methods.

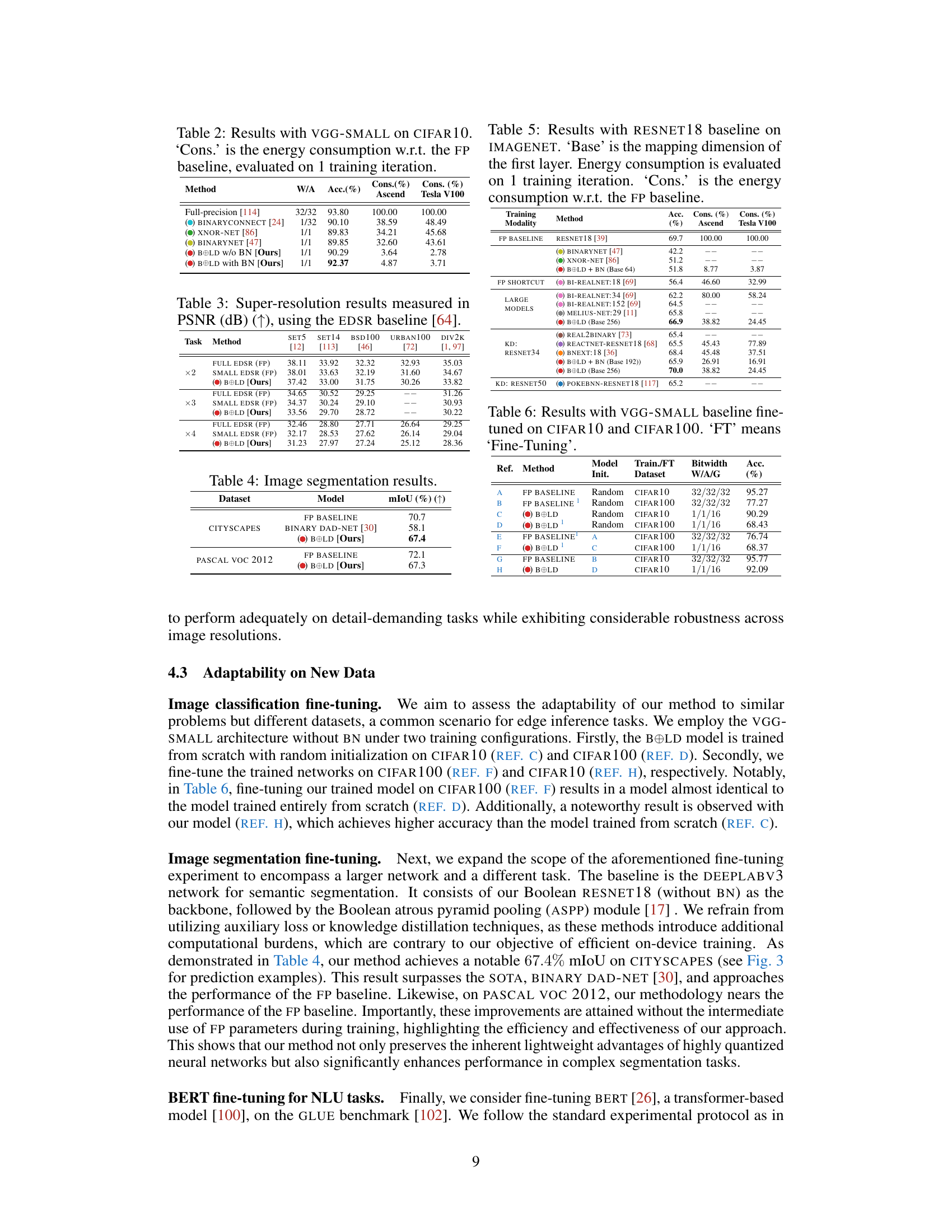
This table presents the results of the VGG-SMALL model on the CIFAR10 dataset. It compares different methods including the full-precision baseline, BINARYCONNECT, XNOR-NET, and BINARYNET, along with the proposed BOLD method both with and without Batch Normalization. The table shows the accuracy achieved by each method, as well as the energy consumption relative to the full-precision baseline. This highlights the energy efficiency of BOLD.
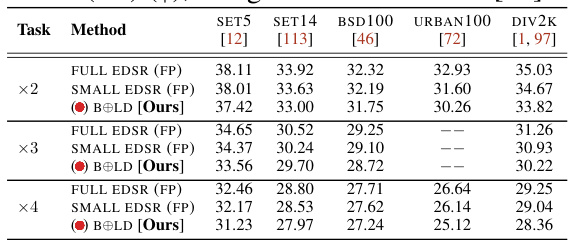
This table presents the Peak Signal-to-Noise Ratio (PSNR) in decibels for different super-resolution models on five benchmark datasets. The models include the full EDSR, a smaller EDSR, and the proposed BOLD method. The results are evaluated for upscaling factors of ×2, ×3, and ×4. Higher PSNR values indicate better image quality.

This table compares the state-of-the-art (SOTA) binarized neural networks (BNNs) with the proposed method BOLD. It highlights key differences in bitwidth, specialized architecture needs, whether full-precision (FP) components are mandatory, and the use of knowledge distillation (KD) during training. The table clearly shows BOLD’s advantages in terms of its simplicity and efficiency compared to existing methods.
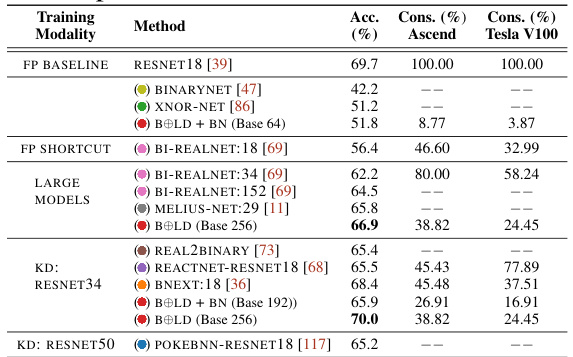
This table compares the performance of different methods, including the proposed BOLD method, on the ImageNet dataset using the RESNET18 architecture. It shows the accuracy achieved by each method and the energy consumption relative to the full-precision baseline for both Ascend and Tesla V100 hardware. Different training modalities are considered, including standard training, fine-tuning using a RESNET34 teacher, and fine-tuning using a RESNET50 teacher.
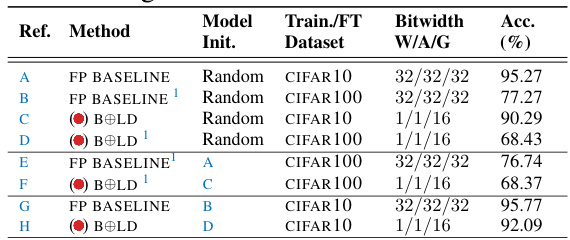
This table presents the results of fine-tuning experiments conducted using the VGG-SMALL baseline model on two different datasets: CIFAR10 and CIFAR100. The table shows the accuracy achieved by various methods, including the full-precision baseline and the proposed BOLD method. It also indicates whether the models were trained from scratch or fine-tuned from a pre-trained model. Bitwidth information for weights, activations and gradients are also shown.

This table compares the state-of-the-art (SOTA) binarized neural networks (BNNs) with the proposed method (BOLD). It highlights key characteristics of each method, including bitwidth (of weights and activations), the use of specialized architectures, the need for full-precision components, whether knowledge distillation (KD) was employed for training, and the type of weight updates and backpropagation used. The comparison reveals that BOLD stands out as the only method not relying on full-precision latent weights for training, while achieving comparable or superior accuracy and significantly lower energy consumption.

This table compares the state-of-the-art (SOTA) binarized neural networks (BNNs) against the proposed method, BOLD. It provides a detailed overview of different aspects of various BNNs, including their weight and activation bitwidths, specialized architecture requirements, use of full-precision components, the application of knowledge distillation (KD) during training, the nature of their weight update mechanisms, and whether or not they utilize backpropagation for training. It highlights the differences in complexity and the training strategies used by different methods, ultimately demonstrating BOLD’s unique capabilities and advantages in terms of efficiency and performance.

This table compares the state-of-the-art (SOTA) binarized neural networks (BNNs) with the proposed method BOLD. It highlights key differences in bitwidth (weight/activation), specialized architecture, mandatory full-precision components, knowledge distillation (KD) usage, weight update methods, backpropagation techniques and the type of arithmetic used. It shows that BOLD differs significantly from existing BNNs, lacking the need for latent-weight-based training, specialized architectures, and intermediate FP components, while still performing competitively in terms of accuracy.

This table compares the state-of-the-art (SOTA) binarized neural networks (BNNs) with the proposed method BOLD. It highlights key differences in bitwidth, specialized architecture requirements, the use of full-precision (FP) components, knowledge distillation (KD) training, and whether backpropagation involves FP latent weights. The table shows that BOLD is unique in that it natively trains Boolean weights, unlike other methods that leverage FP weights during training. This difference contributes to BOLD’s improved efficiency and complexity.
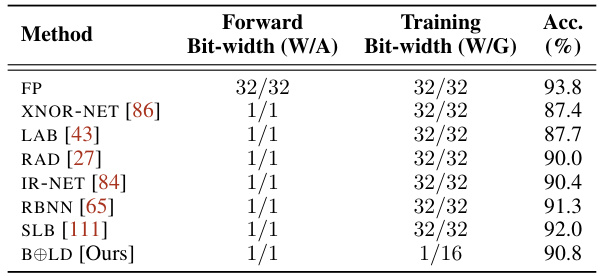
This table presents the results of the experiments conducted using VGG-SMALL on CIFAR10 dataset. The results are compared to those of various other methods like XNOR-NET, BINARYNET, etc. The table shows the accuracy, energy consumption (relative to FP baseline) using the Ascend and Tesla V100 hardware architectures. The results show that the BOLD method achieves higher accuracy than most other methods with only a fraction of the energy cost.

This table compares the state-of-the-art (SOTA) binarized neural networks (BNNs) against the proposed method BOLD. It highlights key differences in bitwidth (of weights and activations), specialized architectures, the use of full-precision (FP) components, knowledge distillation (KD) training techniques, and the weight update backpropagation methods. The table reveals that BOLD uniquely operates directly on native Boolean weights without relying on FP components or KD, offering a more efficient and scalable training approach.
This table compares the state-of-the-art (SOTA) binarized neural networks (BNNs) with the proposed Boolean Logic Deep Learning (BOLD) method. It highlights key differences in bitwidth, specialized architecture needs, mandatory full-precision components, knowledge distillation (KD) usage, and training strategies to provide a comprehensive comparison of efficiency and complexity.

This table compares the state-of-the-art (SOTA) binarized neural networks (BNNs) with the proposed method BOLD. It provides a detailed comparison across various aspects such as the bitwidth of weights and activations, specialized architecture, the use of full-precision components, knowledge distillation (KD) training, and the type of weight update method used. The table highlights the differences and advantages of BOLD over existing SOTA methods.
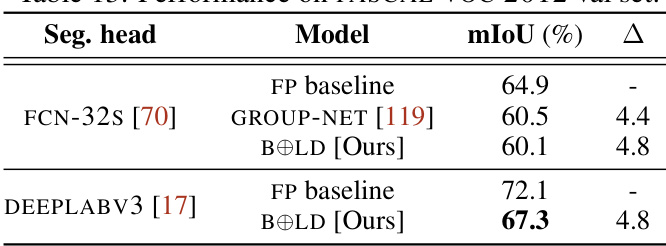
This table presents the results of experiments performed using the VGG-SMALL model on the CIFAR10 dataset. It compares the performance of different methods, including the full-precision baseline, and various binarized neural network approaches. The table shows accuracy, as well as energy consumption relative to the full-precision baseline, offering a comprehensive comparison of accuracy vs. efficiency.

This table compares the state-of-the-art (SOTA) binarized neural networks (BNNs) against the proposed method BOLD. It highlights key differences in bitwidth (for weights and activations), specialized architectures, the use of full-precision (FP) components, knowledge distillation (KD) during training, and whether the method requires weight updates and backpropagation using FP latent weights. BOLD is distinguished by its native Boolean weight and activation training, eliminating the need for FP approximations commonly found in other BNNs.

This table compares state-of-the-art binarized neural networks (BNNs) with the proposed method (BOLD). It shows the bitwidth used for weights and activations, whether specialized architectures are used, if full-precision components are mandatory, and if multi-stage training or knowledge distillation (KD) is employed. BOLD is the only method without full precision components and without needing multi-stage training. This highlights the efficiency and flexibility advantages of the BOLD architecture.

This table compares state-of-the-art (SOTA) binarized neural networks (BNNs) with the proposed Boolean Logic Deep Learning (BOLD) method. It highlights key differences in bitwidth, specialized architecture, use of full-precision (FP) components, knowledge distillation (KD) training, the type of weight updates, backpropagation methods, and the type of arithmetic performed. The table shows that BOLD offers advantages by being free from FP components and KD, leading to enhanced efficiency.

This table compares the state-of-the-art (SOTA) binarized neural networks (BNNs) with the proposed method BOLD. It highlights key differences such as bitwidth (weight-activation), specialized architectures, the use of full-precision (FP) components, knowledge distillation (KD), weight update methods, backpropagation, training arithmetic, and FP latent weights. The table shows that BOLD is unique in its direct use of Boolean weights without relying on FP latent weights, which leads to improved energy efficiency.

This table compares state-of-the-art (SOTA) binarized neural networks (BNNs) with the proposed BOLD method. It highlights key differences in terms of bitwidth (for weights and activations), specialized architecture requirements, the use of full-precision (FP) components, the need for knowledge distillation (KD) during training, and the use of backpropagation and FP latent weights during training. The table shows that BOLD offers a unique approach, eliminating the need for several features prevalent in previous methods while still achieving competitive accuracy.

This table compares the state-of-the-art (SOTA) binarized neural networks (BNNs) with the proposed Boolean Logic Deep Learning (BOLD) method. It highlights key differences across various aspects, such as bitwidth (for weights and activations), specialized architecture requirements, whether full-precision (FP) components or knowledge distillation (KD) are mandatory, the training method (multi-stage training), and what type of arithmetic is used. The table helps to show how BOLD stands out by using Boolean operations natively, eliminating the need for FP components and multi-stage training methods.

This table compares the state-of-the-art (SOTA) binarized neural networks (BNNs) against the proposed BOLD method. It highlights key differences in bitwidth, specialized architecture requirements, the use of full-precision (FP) components, knowledge distillation (KD), weight update methods, backpropagation, and the arithmetic used. This allows for a clear comparison of efficiency and complexity among various BNN approaches.
Full paper#