Dynamics of Supervised and Reinforcement Learning in the Non-Linear Perceptron

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in neural networks and machine learning because it provides a novel and robust method to analyze learning dynamics in nonlinear perceptrons, a fundamental building block of complex neural networks. The new approach is verified with real-world datasets and helps researchers understand the effects of various factors, such as input noise and learning rules, on the learning process. This opens up new avenues for designing more efficient and robust learning algorithms.

Visual Insights

#

This figure illustrates the learning dynamics in a nonlinear perceptron. Panel A shows the perceptron model, where weights ‘w’ map inputs ‘x’ to output ‘ŷ’. Panel B depicts the input data distribution as two multivariate normal distributions with labels ‘y = ±1’, with the weight vector ‘w’ being orthogonal to the classification boundary. Panel C demonstrates how the stochastic nature of the update equations leads to a probability distribution flow of weights over time.

In-depth insights

#

Nonlinear Perceptron Dynamics

#

The study of nonlinear perceptron dynamics offers crucial insights into the learning process within neural networks. Nonlinearity, unlike in simpler linear models, introduces complexities in understanding how the perceptron adapts to data. The research likely explores how different learning rules, such as supervised and reinforcement learning, affect the perceptron’s weight updates and learning curves within this nonlinear context. The influence of input data distribution is also likely investigated; the characteristics of the input data significantly affect the learning process in nonlinear systems. Noise in the input data, another key component, further complicates the dynamics, impacting the learning speed and the stability of learned patterns. Analyzing how noise affects learning across different learning paradigms is a key aspect. The core of the analysis probably involves deriving and solving differential equations that model the evolution of the perceptron’s weights over time. The aim is likely to provide a comprehensive mathematical framework that captures the impact of nonlinearities, data distribution, and noise on the learning process, with the ultimate goal of building more efficient and robust neural networks. Validation of this framework using real-world data, such as the MNIST dataset, is critical for verifying the theoretical findings and assessing the practical applicability of the approach.

Stochastic Process Approach

#

The heading ‘Stochastic Process Approach’ suggests a methodological focus on modeling the learning dynamics of neural networks using stochastic processes. This approach acknowledges the inherent randomness in learning, stemming from noisy input data and the learning rule itself. By treating weight updates as a stochastic process, the authors move beyond deterministic models, offering a more realistic representation of learning in both artificial and biological neural networks. This framework likely allows for analyzing the evolution of the probability distribution of network weights over time and potentially deriving flow equations describing this evolution. A key advantage is the capacity to capture the effects of various factors (input noise, learning rule, task structure) on the overall learning dynamics without linearizing the system. This is crucial because neural network nonlinearities significantly impact learning, and linear approximations often fail to capture this. The stochastic process approach thus provides a robust, nuanced way to understand the complex interplay of these factors, which is especially important for more sophisticated neural network architectures than the simple perceptron studied here.

Input Noise Effects

#

The research explores how input noise impacts learning dynamics in a nonlinear perceptron, revealing non-intuitive effects depending on the learning rule used (supervised or reinforcement). For supervised learning, noise along the coding direction slows down learning, while noise orthogonal to it speeds it up. Reinforcement learning shows a different trend, indicating that the relationship between noise and learning speed is more complex and depends on the input data distribution. The study highlights a trade-off between learning speed and the rate of forgetting previously learned tasks. High input noise leads to faster learning but also accelerates forgetting, while lower noise slows learning but preserves previously acquired knowledge. This nuanced impact of noise on learning suggests the need for careful consideration when designing learning systems, particularly those intended for continual learning scenarios.

Continual Learning Curve

#

Continual learning, the ability of a system to learn new tasks without forgetting previously learned ones, is a significant challenge in machine learning. A continual learning curve would visually represent this process, tracking performance on both old and new tasks as the system encounters them. Catastrophic forgetting, where the acquisition of new knowledge obliterates prior learning, is a crucial factor influencing the shape of this curve. An ideal continual learning curve would display a relatively flat line for older tasks while exhibiting improvement on newer ones, demonstrating successful knowledge retention and transfer. Factors like the learning algorithm, the similarity between tasks, and the presence of noise all significantly affect the curve’s trajectory, potentially leading to sharp declines in performance on older tasks or slow convergence on new ones. Analyzing these curves provides invaluable insights into the effectiveness of different continual learning strategies and helps identify critical areas for improvement. The input data distribution and the chosen learning rule also play significant roles in determining the curve’s characteristics; noise can be especially detrimental, hastening forgetting, while effective learning rules promote graceful knowledge maintenance.

MNIST Dataset Test

#

The MNIST dataset test section would likely assess the model’s generalization ability on real-world data. The authors likely trained their nonlinear perceptron on a subset of the MNIST dataset and then evaluated its performance on a held-out test set. Key performance metrics would include classification accuracy, potentially broken down by digit, and possibly other metrics such as precision and recall. Analysis of the results may involve comparing the model’s performance to existing state-of-the-art results, providing evidence of its effectiveness. A successful MNIST test would strengthen the paper’s claims by demonstrating the practical applicability of their theoretical model and would be a crucial validation of their approach. It would be interesting to see how factors like input noise, learning rules, and regularization parameters influenced the performance on this complex, real-world dataset. The findings from the MNIST tests would offer valuable insights into the model’s robustness and potential limitations, paving the way for future research on more complex tasks.

More visual insights

#

More on figures

This figure displays the results of simulations and analytical calculations of the learning dynamics of a nonlinear perceptron performing binary classification, using both supervised learning (SL) and reinforcement learning (RL). Panels A and B show vector fields representing the weight dynamics for SL and RL, respectively, with example trajectories. Panels C and D compare simulation and analytical results for the learning curves of SL and RL under different noise levels. Panel E illustrates how the asymptotic weight norm (the final magnitude of the weight vector) depends on the regularization parameter λ.

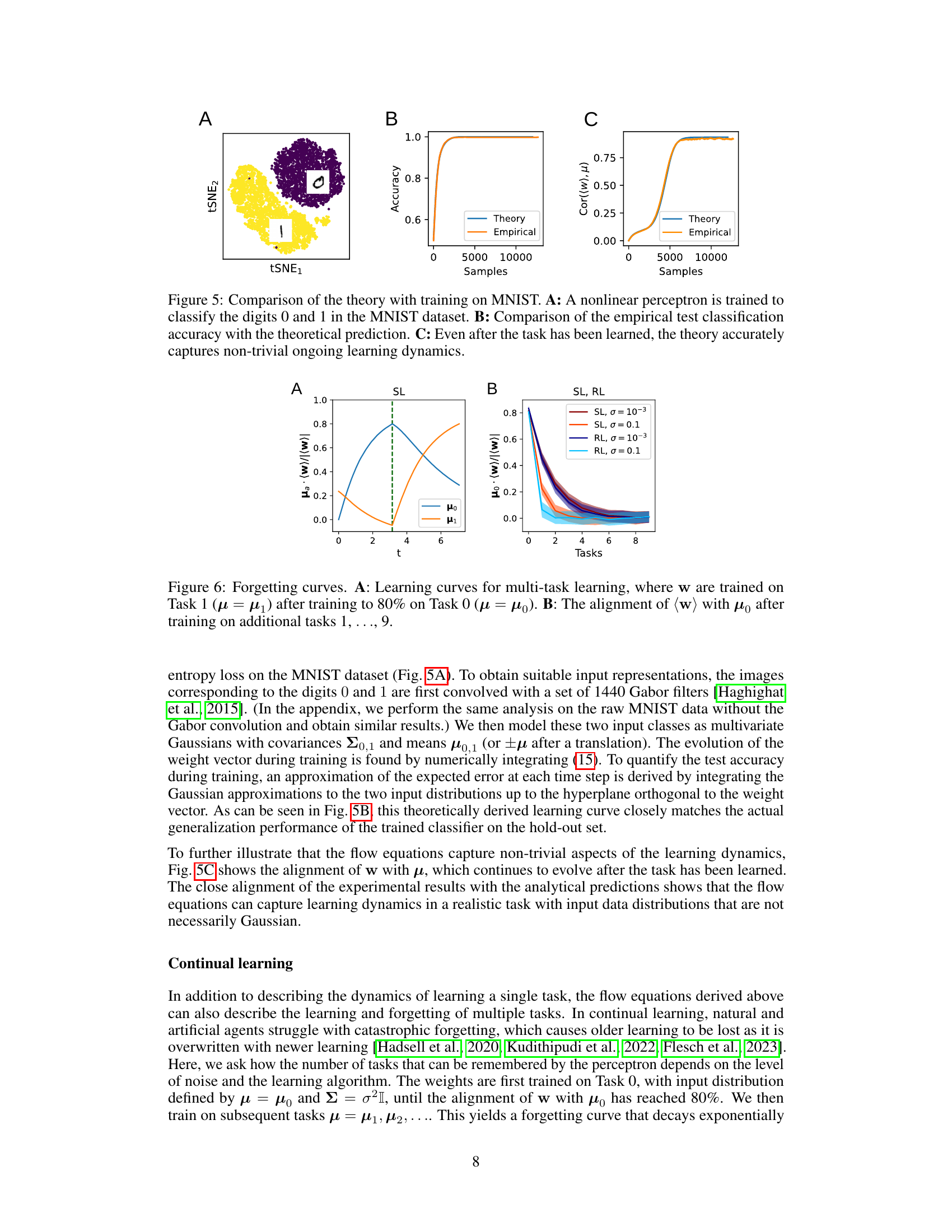
This figure shows the relationship between input noise and the time it takes for a perceptron to learn a classification task. Panel A demonstrates that for isotropic noise, increasing the noise level leads to faster learning. Panel B illustrates how anisotropic noise, where the variance is different along different directions, is characterized. Panel C shows that when anisotropic noise is shifted towards the decoding direction, learning slows down. The figure highlights the effects of both isotropic and anisotropic input noise on learning time, demonstrating differences between supervised and reinforcement learning.

This figure shows how the total variance of the weight vector w changes over time (t) for both supervised learning (SL) and reinforcement learning (RL) under different levels of isotropic input noise (σ). Panel A displays the results for SL, while Panel B shows the results for RL. Each panel shows curves for three different noise levels (σ = 0, σ = 0.5, and σ = 1). The y-axis represents the trace of the weight covariance matrix (tr(Cov(w))), a measure of the overall spread or uncertainty in the weight vector. The key observation is that higher input noise leads to a faster decay in the total variance, meaning the weights converge more quickly to a stable solution. This behavior is observed for both SL and RL, indicating a consistent effect of noise on the learning process.

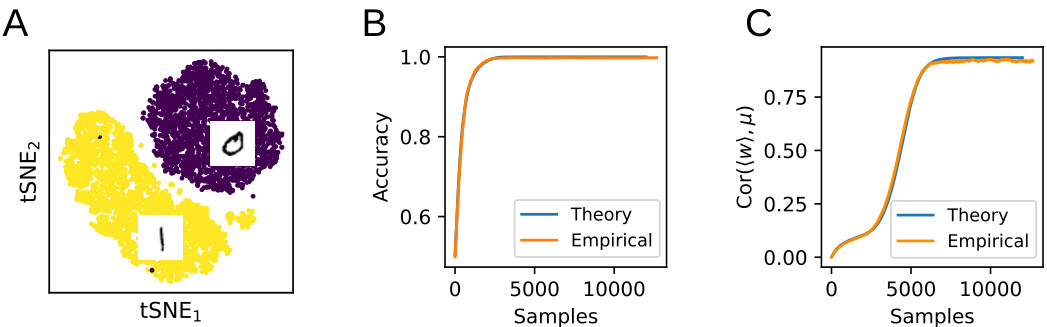
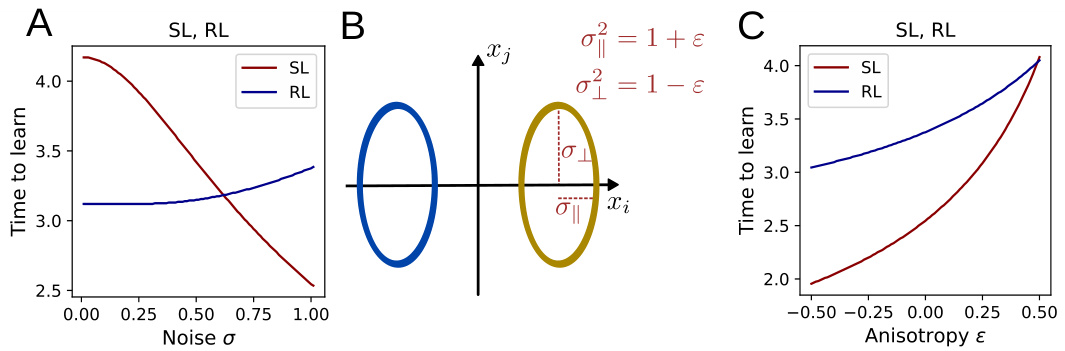
This figure compares the theoretical predictions of the paper’s model with actual results from training a nonlinear perceptron on a subset of the MNIST dataset. Panel A shows a t-SNE visualization of the data, illustrating the separation of the two classes (digits 0 and 1). Panel B compares the theoretical and empirical test classification accuracy over the training process. Panel C shows the correlation between the weight vector (w) and the mean of the data distribution (µ), demonstrating how the theory accurately reflects the learning dynamics even after the task is learned.

Figure 6 demonstrates the continual learning process. Panel A presents learning curves for two tasks, showing how the weights (w) are trained on Task 1 after reaching 80% accuracy on Task 0. Panel B illustrates the forgetting curve, demonstrating the decline in alignment between the weights and the initial task (μ₀) as more tasks are introduced. This figure quantifies the effects of continual learning, highlighting the trade-off between learning new tasks and forgetting previously learned ones.

This figure compares the theoretical predictions of the model with empirical results from training a nonlinear perceptron on the MNIST dataset to classify the digits 0 and 1. Panel A shows a t-SNE embedding of the weight vectors during training. Panel B compares the empirical test accuracy with the theoretical prediction based on the model’s equations. Panel C demonstrates that even after the task is learned, the model accurately captures the ongoing learning dynamics, suggesting its continued validity beyond initial learning.

Full paper

#