↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Robust routing problems, like the Traveling Salesman Problem (TSP), are notoriously difficult to solve when travel times are uncertain. Traditional methods struggle with the computational complexity, especially as the problem size grows. Furthermore, these methods often fail to provide solutions robust enough to handle unpredictable real-world scenarios.
This paper introduces a novel solution using neural networks. The authors develop an end-to-end neural model that leverages a dual multi-head cross-attention mechanism to effectively extract features from uncertain travel time data, ultimately generating robust routes. The model minimizes the maximum deviation from optimal solutions in the worst-case scenario, which is effectively demonstrated using experiments with robust TSP and VRP, significantly outperforming other methods in efficiency.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in robust optimization and neural combinatorial optimization. It presents a novel neural approach for solving robust routing problems, a significant challenge in logistics and operations research. The work’s efficiency and effectiveness, particularly for large-scale problems, are valuable. Furthermore, the generalizability of the method to various robust routing scenarios opens new avenues for further research in this rapidly advancing field.
Visual Insights#

This figure illustrates an example of the Robust Traveling Salesman Problem (RTSP) with interval uncertainty. Panel (a) shows the graph with the interval travel times for each edge. Panel (b) highlights a sample solution (green edges) and its corresponding worst-case scenario (where uncertainty maximizes regret; shown by edge values). Panel (c) shows the optimal TSP solution under the worst-case scenario.
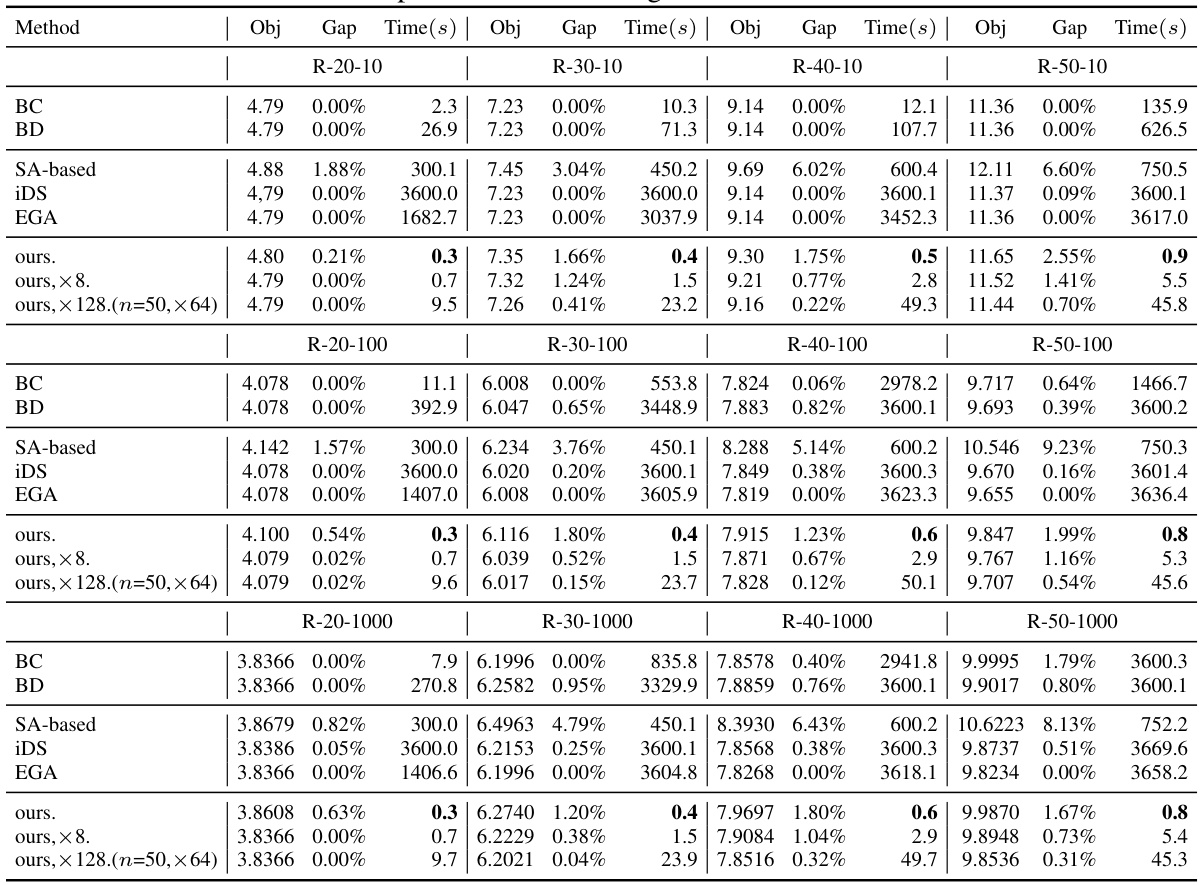
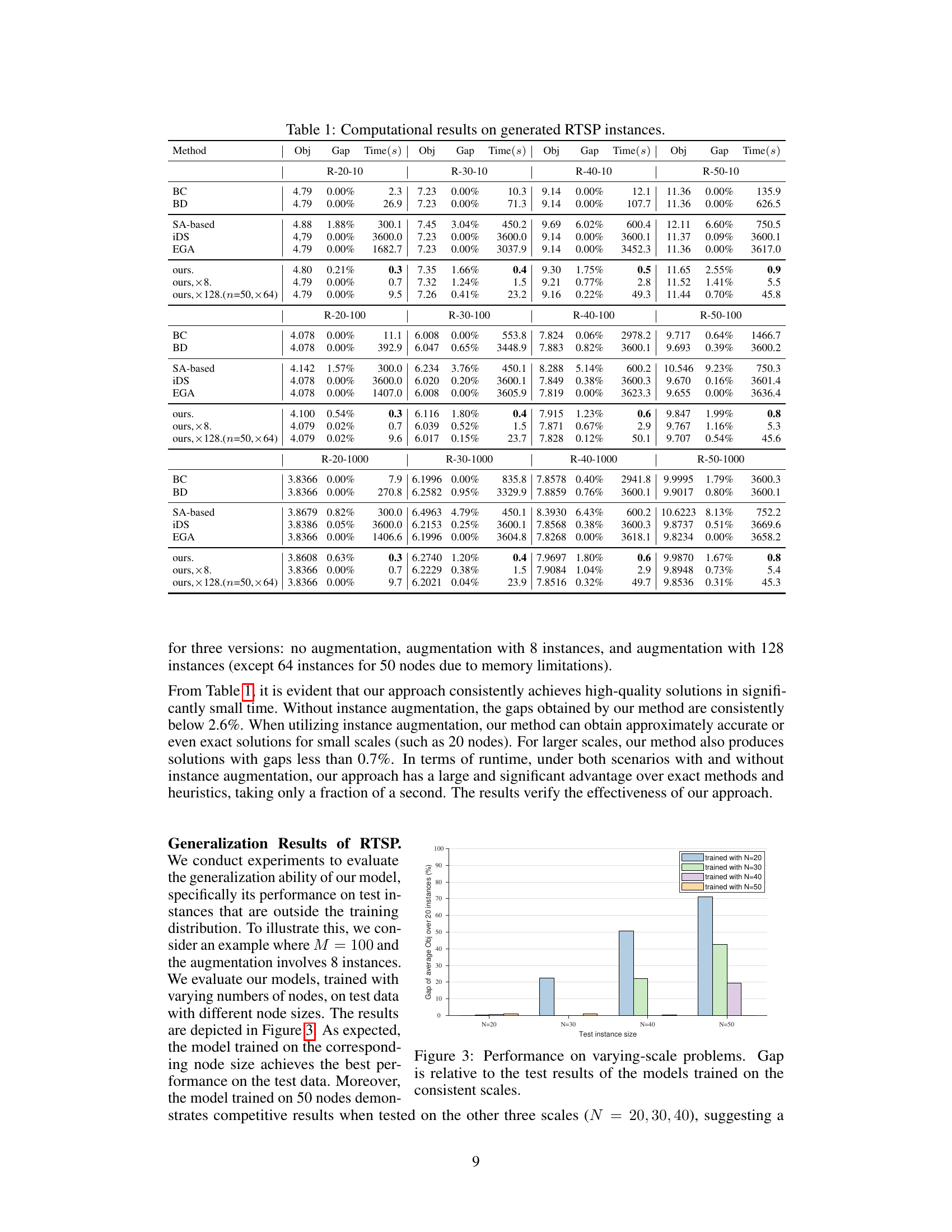
This table presents the computational results of various methods on randomly generated RTSP instances. It compares the performance of exact methods (BC, BD), heuristic methods (SA-based, iDS, EGA), and the proposed neural combinatorial optimization method (ours) across different problem scales (R-20-10, R-30-10, R-40-10, R-50-10, R-20-100, R-30-100, R-40-100, R-50-100, R-20-1000, R-30-1000, R-40-1000, R-50-1000). For each method and problem instance, the table reports the objective value (Obj), the optimality gap (Gap), and the solving time (Time). The proposed method is tested with different levels of instance augmentation (no augmentation, augmentation with 8 instances, and augmentation with 128 instances).
In-depth insights#
Robust Routing#
Robust routing tackles the challenge of finding optimal routes in the presence of uncertainty. Traditional routing algorithms often fail under real-world conditions where travel times, demands, or other factors are unpredictable. Robust routing addresses this by incorporating uncertainty explicitly into the optimization process. Various approaches exist, including stochastic methods that model uncertainty probabilistically and robust optimization techniques that focus on finding solutions that perform well under the worst-case scenario. A key consideration is the trade-off between robustness and optimality; more robust solutions might be less efficient in ideal conditions. The choice of the appropriate method depends heavily on the specific application and the nature of the uncertainties involved. Recent advancements leverage machine learning and AI to improve the efficiency and scalability of robust routing algorithms, particularly in complex scenarios with large-scale data and intricate constraints. The area is rapidly evolving, with ongoing research focused on developing more effective algorithms and understanding the impact of different uncertainty models.
Neural Optimization#
Neural optimization techniques offer a powerful approach to solving complex optimization problems, especially those that are computationally intractable using traditional methods. The core idea is to leverage the power of neural networks to learn effective solutions or policies that guide the search for optima. This can be particularly advantageous in scenarios with noisy data, high dimensionality, or non-convex landscapes where gradient-based methods struggle. Different neural architectures, such as recurrent neural networks or graph neural networks, can be tailored to specific problem structures, like those found in traveling salesman problems or vehicle routing problems. The success of neural optimization hinges on the ability to effectively represent the problem, usually through embeddings that capture relevant features. The training process often involves reinforcement learning or supervised learning, using carefully designed reward functions or datasets of optimal solutions. While powerful, limitations include the need for large training datasets, the potential for overfitting, and the interpretability of learned solutions. Future research should explore techniques to improve generalizability, interpretability, and computational efficiency of these methods.
Budget Uncertainty#
The concept of ‘Budget Uncertainty’ in robust optimization problems, particularly within the context of routing problems like the Traveling Salesman Problem (TSP) and Vehicle Routing Problem (VRP), is crucial for balancing solution robustness and computational tractability. It introduces a parameter (often denoted as Γ) that limits the number of uncertain parameters (e.g., travel times) that can deviate from their nominal values simultaneously. This approach moves beyond overly conservative interval uncertainty sets, allowing for a more realistic modeling of uncertainty while preventing the combinatorial explosion that would occur if all parameters could deviate arbitrarily. The budget uncertainty set provides a flexible way to tune the level of conservatism, offering a trade-off between solution quality (optimality under the worst-case scenario) and computational cost. This parameter is vital in finding practical solutions, as it prevents excessive conservatism when dealing with large-scale instances. In essence, the budget uncertainty set allows for a more nuanced and practical approach to robust optimization by controlling the extent of deviations considered in the worst-case scenario, leading to both more realistic solutions and more manageable computational demands.
Dual Attention#
The concept of ‘Dual Attention’ in a research paper likely refers to a mechanism that employs two separate attention modules, each focusing on different aspects or representations of the input data. This could involve using two distinct attention heads operating simultaneously to capture complementary information or a system where one attention module processes one data type, such as visual features, while another focuses on a different type, such as textual features. The duality might enhance the model’s capacity to integrate diverse information sources, leading to richer feature representations. This approach could be especially beneficial for tasks requiring holistic understanding, integrating context from multiple modalities or perspectives. The effectiveness depends on factors like the specific attention mechanisms used, how the dual attention outputs are combined, and the nature of the data. A key benefit could be improved performance and model robustness by leveraging complementary information for more accurate and comprehensive predictions, but the overall design and implementation are crucial for achieving this.
Future Work#
Future research could explore several promising avenues. Extending the model to handle more complex uncertainty sets beyond the budget uncertainty set is crucial for broader applicability. Investigating alternative neural architectures, such as graph neural networks or transformers, could potentially improve efficiency and scalability. A significant area for advancement is developing more sophisticated reward functions that better capture the trade-off between robustness and optimality. Empirical evaluations on larger-scale real-world datasets would provide stronger evidence of the model’s practical performance. Finally, exploring the application of this framework to other combinatorial optimization problems, such as the vehicle routing problem with time windows or the generalized assignment problem, is warranted to assess its generalizability and impact. Addressing these aspects would significantly enhance the robustness and applicability of the neural combinatorial optimization approach to the robust routing problem.
More visual insights#
More on figures

This figure illustrates the complete solution framework of the proposed neural combinatorial optimization method for solving the robust routing problem. The framework uses an encoder-decoder structure. The encoder takes the input data (Up_Matrix and Low_Matrix) representing the upper and lower bounds of travel times between nodes and extracts problem features using a MatNet model. The decoder uses masked multi-head cross-attention and a single attention and scaling mechanism to generate a probability distribution over the next node to visit in the route. A pre-trained TSP model calculates the reward (r) based on the max-regret value of the completed route, which is used to train the policy network. The reward is zero until a complete route is generated, making it a sparse reward.

This figure shows the generalization ability of the model trained on different sizes of the RTSP problem (N = 20, 30, 40, and 50). The x-axis represents the size of test instances (N), while the y-axis displays the average optimality gap percentage across 20 instances. The bars illustrate the performance of models trained on various sizes of training datasets. The results show that models trained on larger datasets achieve better generalization, specifically with the model trained on 50 nodes demonstrating competitive results even when tested on smaller datasets.

This figure illustrates an example of the Robust Traveling Salesman Problem (RTSP) with interval uncertainty. Part (a) shows the graph with edges having travel times defined by intervals. Part (b) shows a specific solution (‘1 → 2 → 3 → 4 → 1’) and its corresponding worst-case scenario, where the travel times on the selected edges reach their upper bounds, while others are at their lower bounds. Part (c) shows the optimal solution for this worst-case scenario.
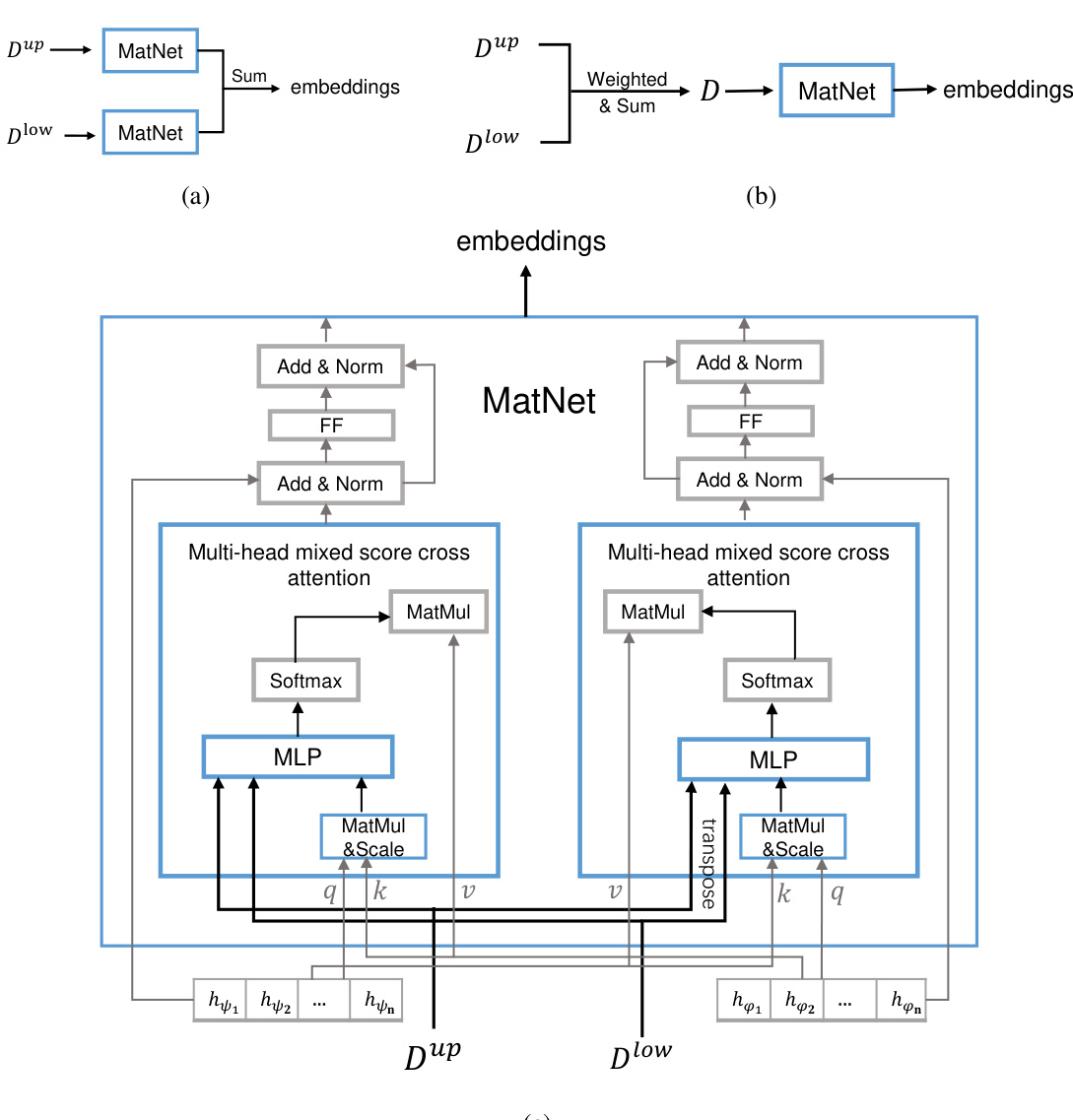
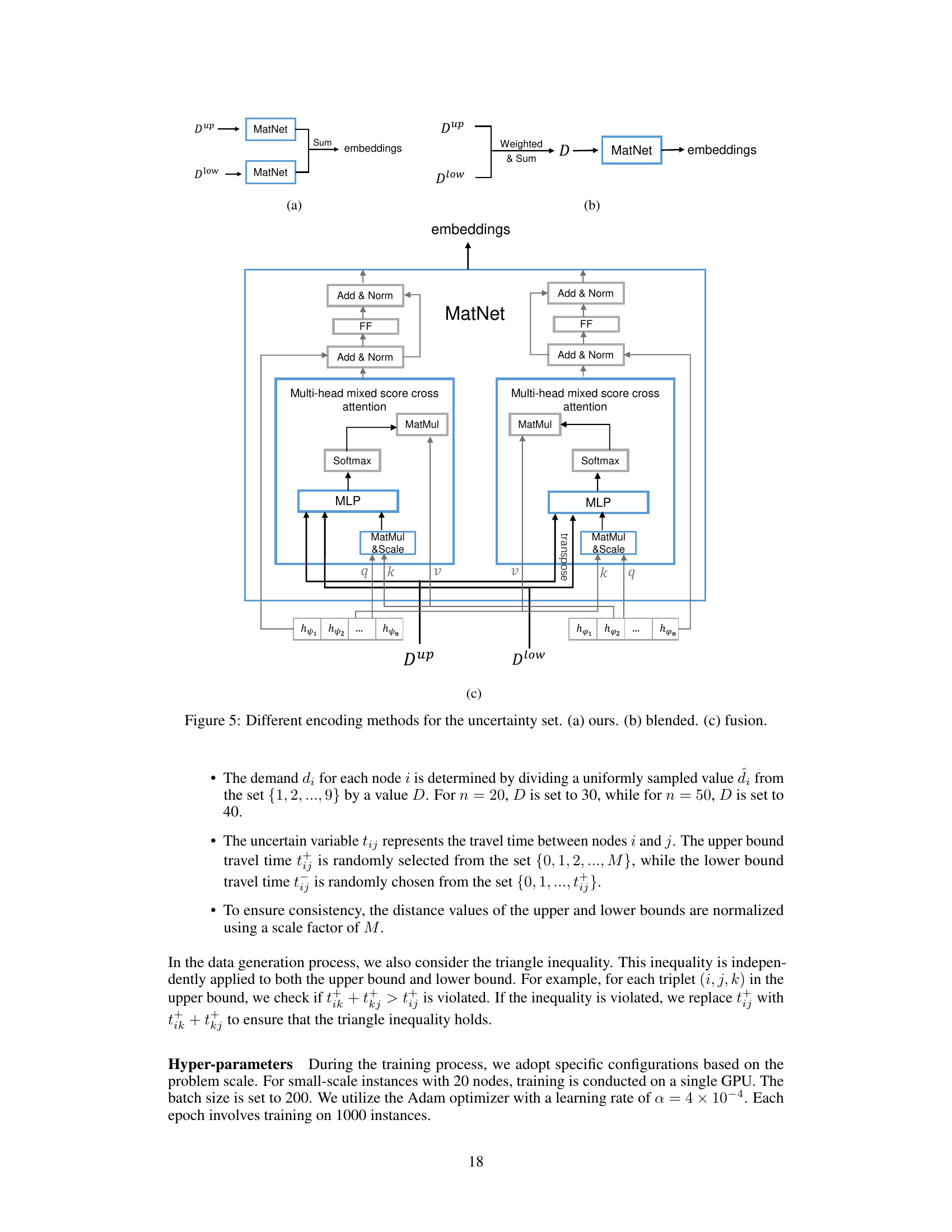
This figure illustrates three different methods for encoding the uncertainty set in the robust routing problem. Method (a) uses a dual-weighted graph approach where the upper and lower bound matrices are processed separately before being combined. Method (b) creates a blended matrix by weighting the upper and lower bound matrices before processing. Method (c) uses a fusion approach where the matrices and attention scores are combined using a multi-layer perceptron (MLP) before being fed into the encoder.

This figure shows the training curves of the proposed neural combinatorial optimization model for solving the Robust Traveling Salesman Problem (RTSP) with 50 nodes and interval uncertainty. The left subplot (a) displays the training loss over 2000 epochs, indicating a decrease in loss as the model learns. The right subplot (b) shows the training score (objective value), also over 2000 epochs, reflecting improvement in solution quality as the training progresses.

This figure illustrates three different methods for encoding the uncertainty set in the robust routing problem. Method (a) uses two separate matrices (one for upper bounds and one for lower bounds) and then combines their embeddings. Method (b) blends the two matrices into a single matrix before encoding. Method (c) fuses the matrices and attention scores using a multi-layer perceptron before encoding. These different approaches are compared to determine which is most effective for handling uncertainty in the model.
More on tables
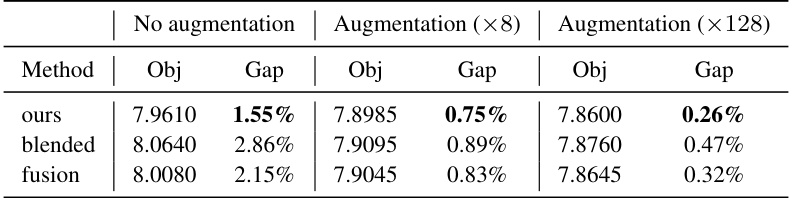
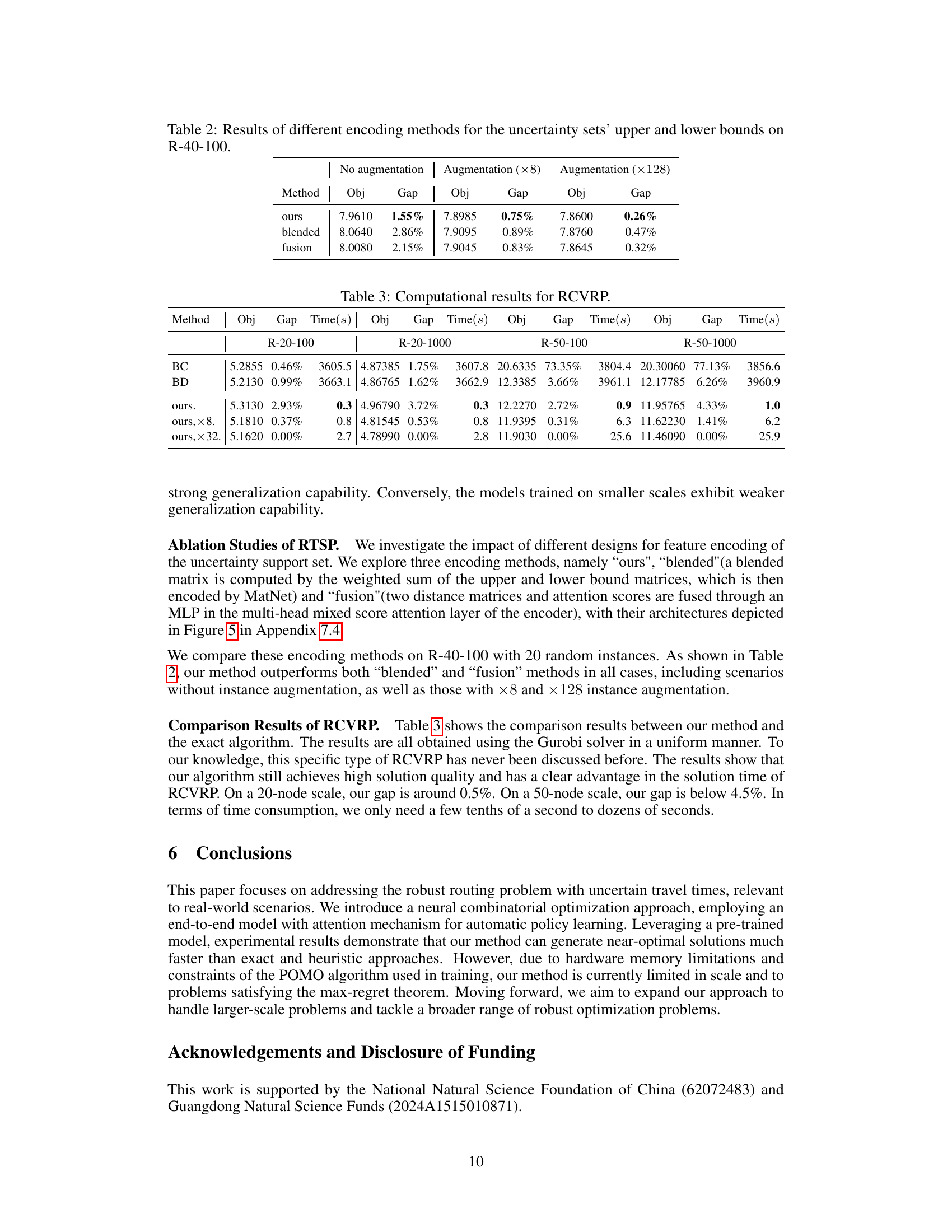
This table presents the results of three different encoding methods for handling the uncertainty sets’ upper and lower bounds in the Robust Traveling Salesman Problem (RTSP). The three methods are: ‘ours’, ‘blended’, and ‘fusion’. The table compares the average objective value (‘Obj’) and the gap (‘Gap’) between the obtained objective value and the optimal value for each encoding method, considering three augmentation levels: no augmentation, augmentation with 8 instances, and augmentation with 128 instances. The results show the effectiveness of the proposed ‘ours’ method compared to the ‘blended’ and ‘fusion’ methods.
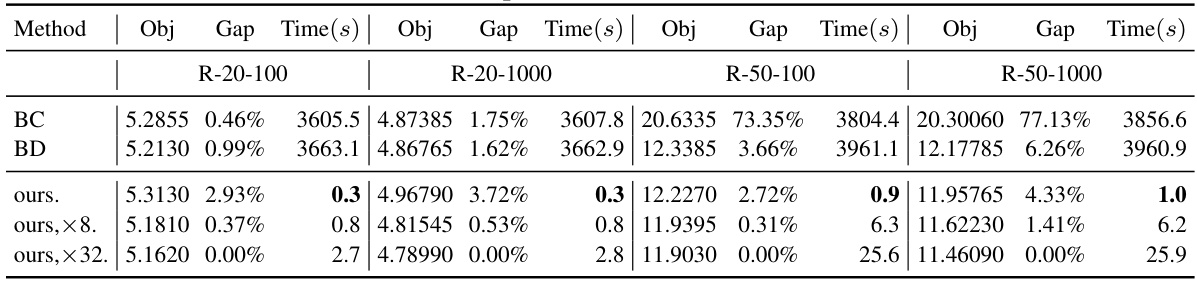
This table presents the results of the proposed neural combinatorial optimization method and other existing methods for solving the Robust Traveling Salesman Problem (RTSP) with different problem sizes (number of nodes). The results include the average objective value obtained by each method, the relative gap between the obtained solution and the best-known optimal value (Gap), and the average solving time per instance (Time). The methods are categorized into three groups: exact methods, heuristic methods, and the proposed method. Different augmentation strategies (no augmentation, augmentation with 8 instances, and augmentation with 128 instances) are also compared for the proposed method. This table demonstrates the computational efficiency and accuracy of the proposed method compared to existing methods.
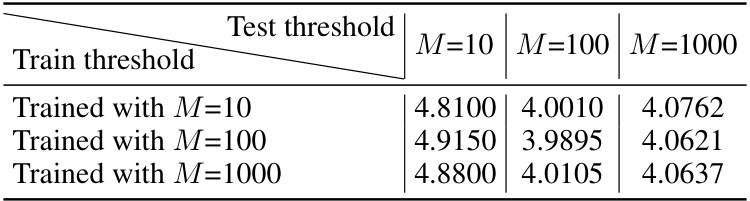
This table presents the results of an experiment evaluating the generalization ability of the trained model on RTSP problems with varying threshold values (M). Three models were trained using different training threshold values (M=10, M=100, M=1000). The performance of each trained model is then tested on instances with different test threshold values (M=10, M=100, M=1000). The table shows the average objective values obtained for each combination of training and testing threshold values. This experiment aims to assess how well the model generalizes to unseen threshold values, thereby demonstrating its robustness and ability to handle different problem characteristics.
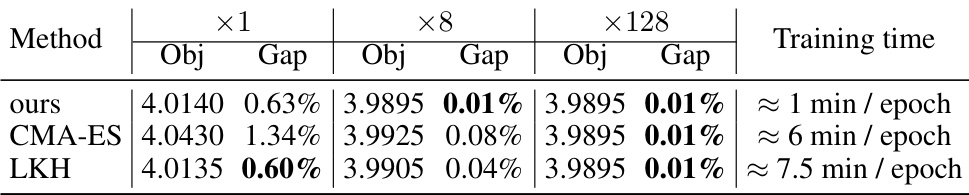
This table compares the performance of three different built-in TSP solving algorithms (ours, CMA-ES, and LKH) on the R-20-100 problem instances. The comparison is done across three augmentation levels (no augmentation, ×8 augmentation, and ×128 augmentation), with each showing the objective value (Obj), optimality gap (Gap), and training time per epoch. The results highlight the effectiveness of the proposed method (‘ours’) in terms of both solution quality and training efficiency.

This table presents a comparison of the results obtained using different values of Γ (gamma), a parameter that controls the robustness of the budget uncertainty set, for the RTSP problem with 20 nodes. The table compares the objective values (‘Obj’) and computation times (‘Time(s)’) for three different values of Γ: Γ = floor(N/2), Γ = floor(N/4), and Γ = 0. These results highlight the impact of Γ on the solution quality and computational efficiency. The ‘ours128’ and ‘ours8’ rows refer to the proposed approach with different levels of instance augmentation.
Full paper#