Make Continual Learning Stronger via C-Flat

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in continual learning due to its novel optimization method, C-Flat, which significantly enhances learning stability. C-Flat addresses the catastrophic forgetting problem, a major challenge in CL, by promoting flatter loss landscapes. This approach is simple, versatile and highly effective across diverse CL methods and datasets. Its plug-and-play nature allows easy integration with existing CL methods, paving the way for improved performance and new research directions. The thorough analysis and experimental results provide a strong baseline for future CL research, opening avenues for exploration in other machine learning subfields.

Visual Insights

#

This figure illustrates the core idea of C-Flat, comparing it to direct tuning and regularization-based approaches. Direct tuning (a) leads to catastrophic forgetting. Regularization (b) provides a balance but suboptimal results. C-Flat (c) achieves better generalization by finding a global optimum with a flatter loss landscape, preventing catastrophic forgetting.

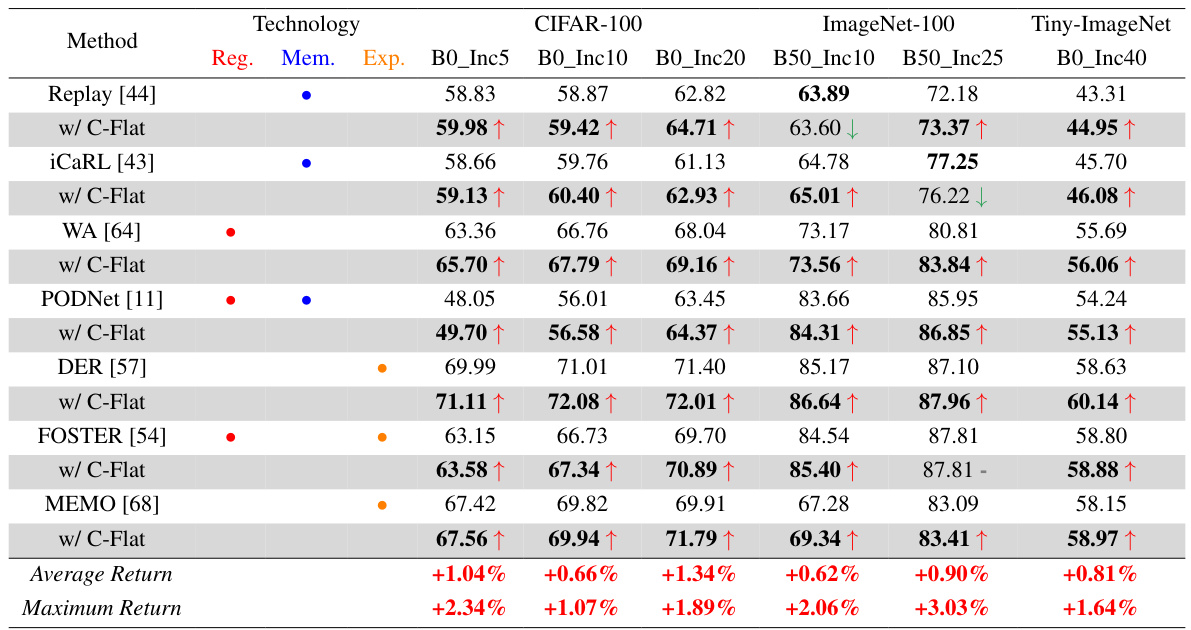
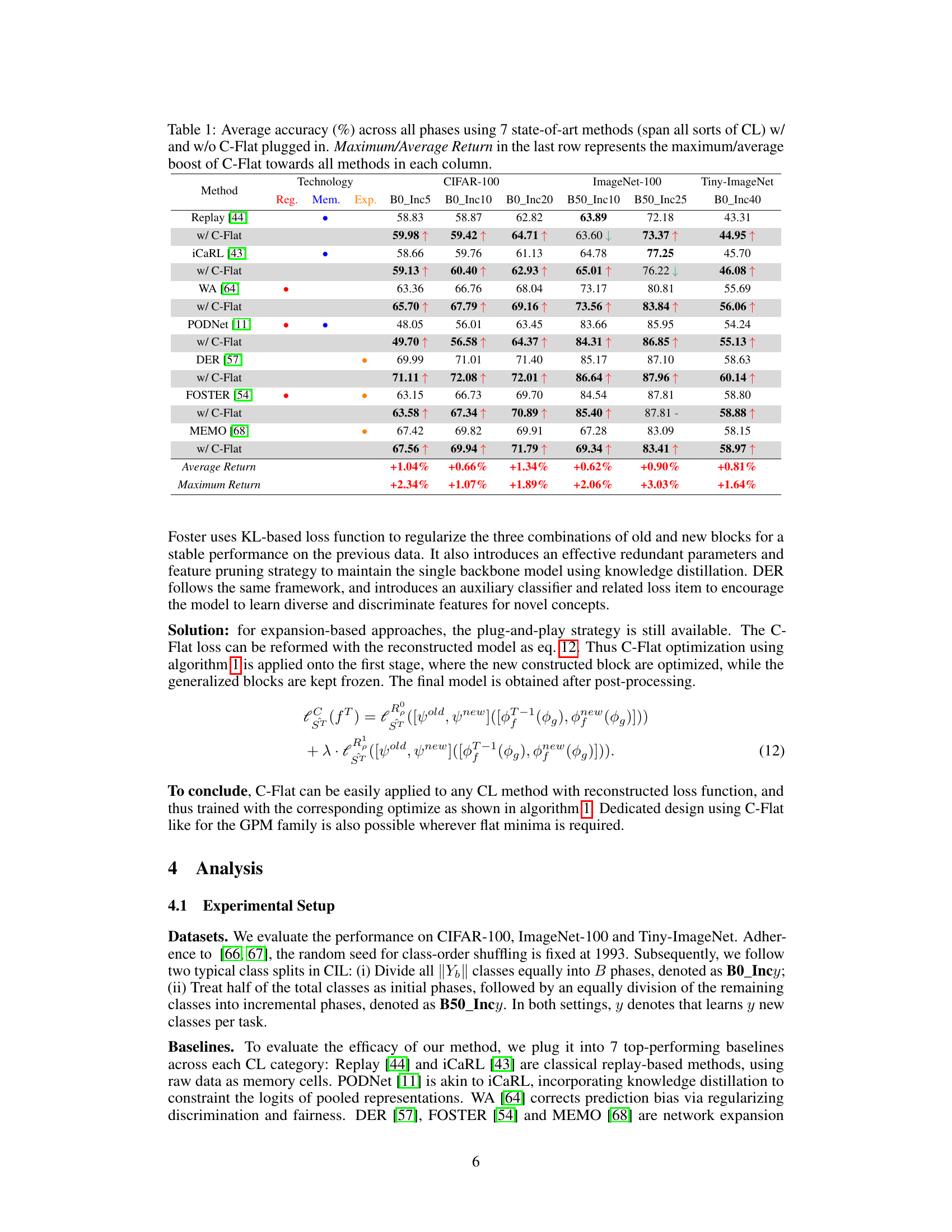
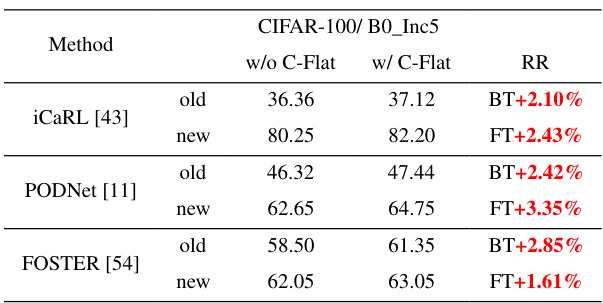
This table presents the average accuracy of seven state-of-the-art continual learning (CL) methods across different benchmark datasets (CIFAR-100, ImageNet-100, and Tiny-ImageNet) and incremental learning scenarios. The results are shown both with and without the proposed C-Flat method integrated. The ‘Average Return’ and ‘Maximum Return’ rows highlight the performance improvement gained by using C-Flat. It demonstrates the consistent performance boost of C-Flat across various CL methods and datasets, showcasing its versatility and effectiveness.

In-depth insights

#

C-Flat: A New Optimizer

#

The heading ‘C-Flat: A New Optimizer’ suggests a novel optimization method for continual learning, likely focusing on addressing catastrophic forgetting. C-Flat’s core innovation probably lies in its approach to loss landscape manipulation, aiming for flatter minima which generally enhance generalization and stability. This contrasts with existing methods that might focus solely on zeroth-order sharpness, potentially leading to overly sharp minima and reduced robustness. The name “C-Flat” itself implies a focus on continual learning (“C”) and a flattened loss landscape (“Flat”). Therefore, the paper likely presents empirical results demonstrating improved performance on various continual learning benchmarks by applying C-Flat to existing continual learning algorithms. The ease of integration, suggested by the ’new optimizer’ framing, is a key selling point, indicating it can be added to existing methods with minimal code changes, improving their overall effectiveness. The implications are significant, potentially leading to wider adoption of better-performing continual learning models across different domains and applications.

Sharpness & Flatness

#

The concepts of sharpness and flatness in loss landscapes are central to the paper’s exploration of continual learning. Sharp minima, often associated with high curvature, are characterized by sensitivity to parameter changes, leading to poor generalization and catastrophic forgetting. Conversely, flat minima, exhibiting low curvature, are considered more robust, offering improved generalization and better memory retention across tasks. The paper highlights the tradeoff between these two characteristics, proposing that while zeroth-order methods prioritize flat minima, they might not always achieve global optimality. The introduction of C-Flat aims to leverage the advantages of flatness while enhancing learning stability and global optimization, effectively addressing the sensitivity-stability dilemma inherent in continual learning by finding a balance between sharp and flat minima that promotes both task-specific learning and knowledge preservation. This approach seeks to overcome the limitations of solely pursuing flat minima by ensuring superior generalization performance.

Unified CL Framework

#

The proposed “Unified CL Framework” aims to address the challenge of catastrophic forgetting in continual learning (CL) by offering a versatile and easily integrable optimization method called C-Flat. C-Flat enhances learning stability by focusing on a flatter loss landscape, improving model generalization across tasks. This contrasts with existing methods that primarily focus on minimizing sharpness, which can sometimes lead to sharper, less generalizable minima. The framework’s “plug-and-play” nature makes it compatible with various CL approaches, including memory-based, regularization-based, and expansion-based methods. The framework’s effectiveness is demonstrated through extensive experiments across diverse datasets and CL categories, showing consistent performance improvements. The emphasis on flat minima and the unified nature of the framework present a significant contribution to the CL field, potentially serving as a valuable baseline for future research in the area.

Computational Efficiency

#

The paper investigates the computational efficiency of its proposed C-Flat optimization method for continual learning. C-Flat aims to enhance learning stability by promoting flatter minima in the loss landscape, a strategy shown to improve generalization. While the method itself adds computational overhead compared to standard optimizers like SGD, the paper demonstrates that significant performance gains can be achieved with only a fraction of the full C-Flat optimization iterations. This suggests that C-Flat’s benefits outweigh the added computational cost. Specifically, the authors show that using just 10% to 50% of the typical C-Flat iterations can yield substantial performance improvements, significantly reducing training time while still providing competitive or superior accuracy compared to baseline methods. This makes C-Flat a more practical option for real-world continual learning applications, offering a favorable trade-off between computational efficiency and performance gains.

Future Research

#

Future research directions stemming from this continual learning (CL) study using C-Flat could involve several promising avenues. Extending C-Flat’s applicability to a wider array of CL scenarios, beyond class-incremental learning, is crucial. This includes exploring its effectiveness in areas like task-incremental learning and domain-incremental learning. Investigating the theoretical underpinnings of C-Flat more deeply is needed to better understand its generalization capabilities and its interaction with different loss landscape characteristics. Developing more robust and efficient methods for estimating Hessian information could improve C-Flat’s performance and practicality. Finally, a comprehensive empirical evaluation of C-Flat across various datasets and network architectures would strengthen its position as a general-purpose CL optimization technique. Addressing these research directions could significantly enhance the field of CL and pave the way for more robust and adaptable AI systems.

More visual insights

#

More on figures

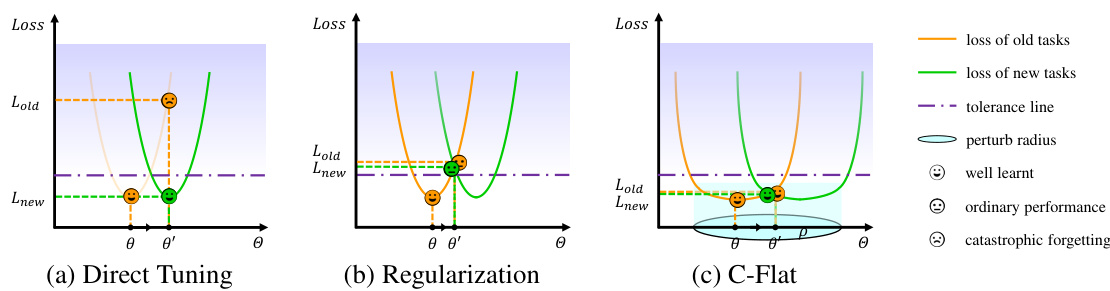
This figure illustrates three different approaches to continual learning (CL) and how they address the issue of catastrophic forgetting. (a) Direct Tuning shows that focusing solely on minimizing the loss of the new task leads to catastrophic forgetting of previous tasks. (b) Regularization attempts to balance the optimization between new and old tasks, but may still lead to suboptimal performance. (c) C-Flat, the proposed method, aims to find a global optima with a flattened loss landscape, thus improving the generalization ability and preventing catastrophic forgetting. The figure highlights the difference in the loss landscape and the optimal points achieved by each method.

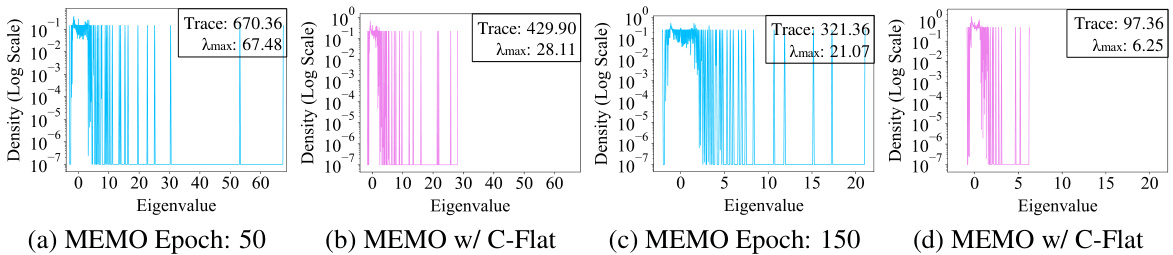
This figure displays the distribution of Hessian eigenvalues and their traces for MEMO (Memory-based method) on the CIFAR-100 dataset with B0_Inc10 setting (10 classes per increment). It compares the results with and without the application of C-Flat optimization. The plots visualize how C-Flat alters the eigenvalue distribution, leading to flatter minima and a smaller trace, indicating improved model generalization and a less sharp loss landscape. The trace is a measure of the overall flatness of the loss landscape, while the maximum eigenvalue represents the sharpness of the loss function. The results showcase that C-Flat leads to flatter minima with smaller eigenvalues and trace values, resulting in improved generalization ability in continual learning.

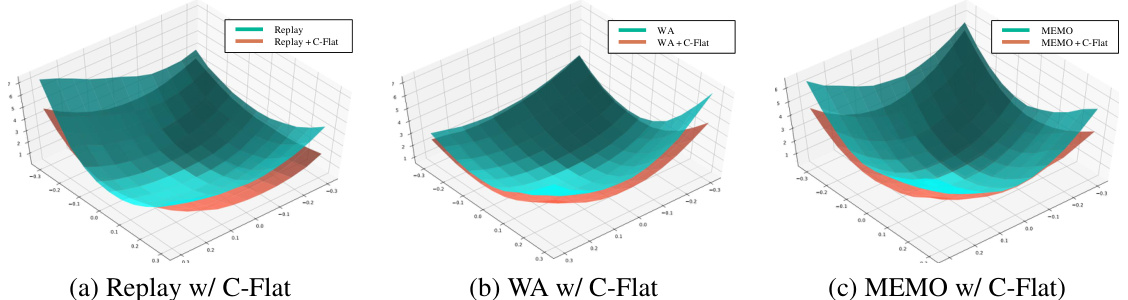
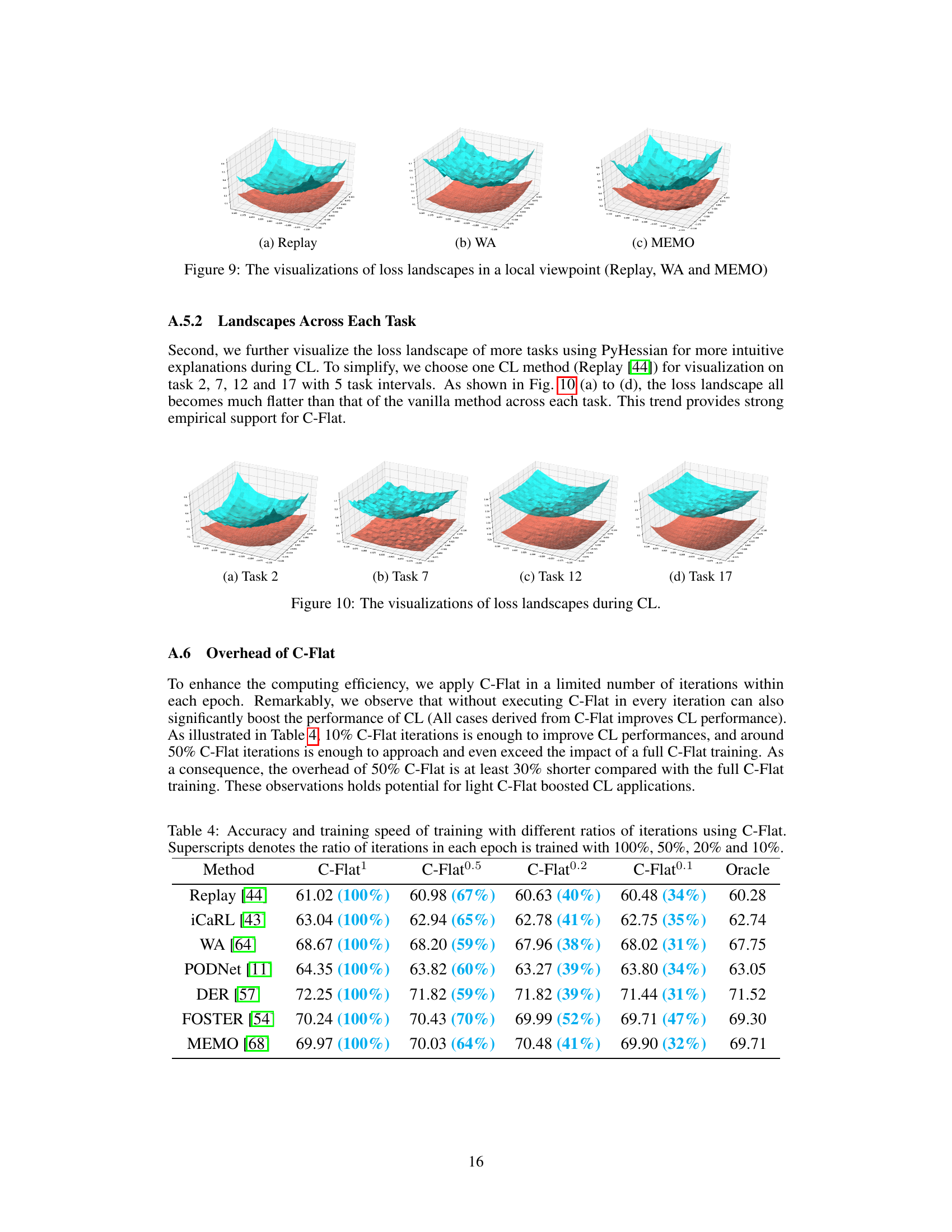
This figure visualizes the loss landscapes of three different continual learning methods: Replay, WA, and MEMO, both with and without the application of C-Flat. By perturbing model parameters around the training completion point (CIFAR-100 dataset, B0_Inc10 setting), the plots illustrate the impact of C-Flat on the shape of the loss landscape, highlighting how it leads to flatter minima compared to the baselines. The visualization uses the first two Hessian eigenvectors.

This figure compares the performance of C-Flat against a zeroth-order flatness method across different continual learning settings (B0_Inc10 and B0_Inc20). It shows average accuracy across multiple continual learning methods (Replay, iCaRL, WA, PODNet, DER, FOSTER, MEMO). The results indicate that C-Flat consistently outperforms the zeroth-order sharpness method, demonstrating its effectiveness in improving model generalization.

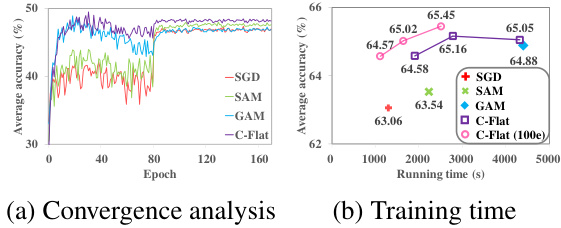
The figure analyzes the computation overhead of the proposed C-Flat optimizer compared to other methods (SGD, SAM, GAM). Subfigure (a) shows the convergence speed and accuracy, demonstrating that C-Flat converges faster and achieves higher accuracy with fewer iterations. Subfigure (b) shows the training time, indicating that C-Flat outperforms other optimizers with less time, especially when using a smaller number of iterations.

This figure presents an ablation study on the hyperparameters λ and ρ of the C-Flat algorithm. Subfigures (a) and (b) show the impact of λ and ρ, respectively, on the performance of three different continual learning methods: WA, Replay, and MEMO. Subfigures (c) and (d) focus on the MEMO method, comparing the effects of ρ and its scheduler on the performance when using different optimizers: SGD, SAM, GAM, and C-Flat. The results visualize how the performance varies with different settings of λ and ρ, offering insight into the algorithm’s sensitivity and robustness.

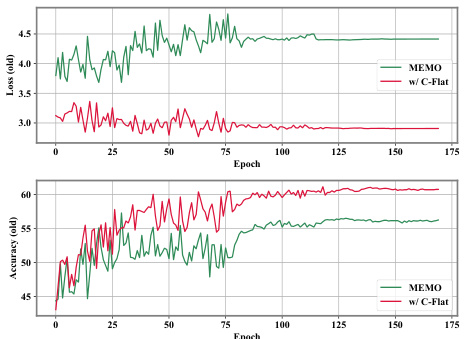
This figure visualizes the change in loss and forgetting of old tasks in continual learning. The top panel shows the loss on old tasks over epochs for both the MEMO method and MEMO with C-Flat. The bottom panel shows the accuracy on old tasks over epochs for both methods. The results indicate that C-Flat leads to lower loss and less forgetting of old tasks during continual learning.

This figure visualizes the loss landscapes of three different continual learning methods: Replay, WA, and MEMO, both with and without the application of C-Flat. By perturbing model parameters around their final trained values along the two largest Hessian eigenvectors, the plots illustrate the shape of the loss surface near the minimum. The goal is to show how C-Flat results in a flatter loss landscape, which is associated with better generalization and less catastrophic forgetting.

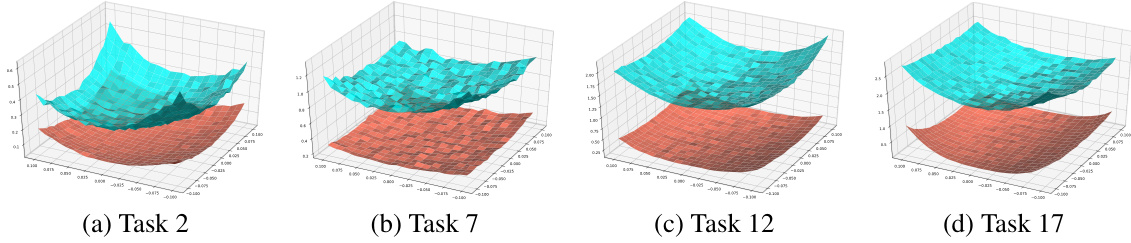
This figure visualizes the loss landscapes at different tasks during continual learning using PyHessian. It shows that the loss landscape becomes flatter when using C-Flat, compared to a baseline method, which supports the claim that flatter loss landscapes improve continual learning performance.

More on tables

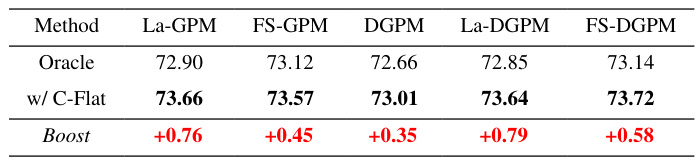
This table presents the results of applying C-Flat to the FS-DGPM series of continual learning methods. It compares the performance of the original FS-DGPM methods (La-GPM, FS-GPM, DGPM, La-DGPM, and FS-DGPM) with the performance after incorporating the C-Flat optimization. The ‘Oracle’ row shows the baseline performance, and the ‘w/ C-Flat’ row shows the performance with C-Flat added. The ‘Boost’ row indicates the improvement in performance achieved by using C-Flat, demonstrating that C-Flat consistently improves the performance of various continual learning approaches.

This table presents the average accuracy achieved by seven state-of-the-art continual learning (CL) methods across multiple benchmark datasets (CIFAR-100, ImageNet-100 Tiny-ImageNet) and different incremental learning scenarios (B0_Inc5, B0_Inc10, B0_Inc20, B50_Inc10, B50_Inc25, B0_Inc40). The results are shown both with and without the proposed C-Flat optimization method. The ‘Maximum/Average Return’ rows indicate the maximum and average improvement in accuracy achieved by incorporating C-Flat into each method.

This table presents the average accuracy of seven state-of-the-art continual learning (CL) methods across three datasets (CIFAR-100, ImageNet-100, and Tiny-ImageNet) and various incremental settings. It compares the performance of each method with and without the proposed C-Flat optimization. The ‘Maximum/Average Return’ rows show the performance improvement achieved by incorporating C-Flat, indicating its effectiveness in boosting the performance of existing CL algorithms.

This table presents the average accuracy achieved by seven state-of-the-art continual learning (CL) methods across multiple benchmark datasets (CIFAR-100, ImageNet-100, Tiny-ImageNet). The results are shown for both the original methods and the same methods with the proposed C-Flat optimization integrated. The ‘Maximum/Average Return’ rows indicate the improvement gained by adding C-Flat, highlighting the consistent performance boost across various CL approaches and datasets.

Full paper

#