TL;DR#
Many machine learning models benefit from incorporating inductive biases, such as symmetries. Recent advancements model physical dynamics through Hamiltonian mechanics, guaranteeing energy conservation. However, manually embedding such constraints can be challenging. This work addresses this challenge by using Noether’s theorem to link symmetries with conserved quantities which can be learned.
This paper proposes “Noether’s Razor,” a novel method that jointly learns the Hamiltonian and conserved quantities. It uses approximate Bayesian model selection, avoiding the need for manual regularization to prevent trivial solutions. This end-to-end training procedure leverages the Occam’s razor effect to find the simplest representation. Experiments on harmonic oscillators and n-body systems demonstrate the efficacy of Noether’s Razor in accurately identifying conserved quantities and symmetries, leading to improved predictive accuracy.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in machine learning and physics because it bridges the gap between symmetry exploitation and Hamiltonian learning. It introduces a novel Bayesian model selection method that automatically learns conserved quantities and their associated symmetries directly from data, opening new avenues for building more accurate and generalizable physics-informed machine learning models and advancing our understanding of symmetry discovery in complex systems.
Visual Insights#

🔼 This figure shows a graphical model representing the probabilistic relationships between different variables in the proposed method. The non-symmetrised observable Fθ acts as a prior on the Hamiltonian function. The conserved quantities Cη influence the Hamiltonian by enforcing symmetries. The symmetrised Hamiltonian H then generates the observed trajectory data X. This model incorporates the concept of Noether’s theorem, linking symmetries to conserved quantities, into a Bayesian framework for learning Hamiltonian systems.
read the caption
Figure 1: Graphical probabilistic model. Trajectory data X depends on a symmetrised Hamiltonian H induced by non-symmetrised observable F and conservation laws C.

🔼 This table compares the performance of three different Hamiltonian neural network (HNN) models on a simple harmonic oscillator task: a vanilla HNN, an HNN with the proposed symmetry learning method, and an HNN with the correct SO(2) symmetry (acting as a reference oracle). The metrics evaluated are training and testing mean squared error (MSE), negative log-likelihood (NLL), Kullback-Leibler divergence (KL), evidence lower bound (ELBO), and negative ELBO. The results demonstrate that the symmetry learning method achieves performance comparable to the reference oracle and significantly outperforms the vanilla HNN, particularly in terms of test MSE.
read the caption
Table 1: Learning Hamiltonian dynamics of the simple harmonic oscillator. We compare a vanilla HNN, our symmetry learning method, and a model with the correct SO(2) symmetry built-in as reference oracle. Our method achieves reference oracle performance, indicating correct symmetry learning, and outperforms the vanilla model by improving predictive performance on the test set.
In-depth insights#
Noether’s Theorem#
Noether’s Theorem, a cornerstone of theoretical physics, elegantly connects symmetries in a system with conserved quantities. Its application in machine learning, as explored in this paper, offers a powerful way to incorporate inductive biases. By framing symmetries as learnable conserved quantities, the model can directly learn these symmetries from data, rather than relying on pre-defined constraints. This approach leverages the principle of Occam’s Razor, favoring simpler models that explain the data effectively while avoiding overfitting by penalizing overly complex or unconstrained hypotheses. The method’s strength lies in its ability to automatically discover and utilize symmetries inherent in the data, improving generalization and predictive accuracy, which contrasts with traditional methods that require manually specifying symmetries. The Bayesian model selection framework provides a natural mechanism for implementing this approach, allowing the model to learn both the Hamiltonian and conserved quantities simultaneously, enhancing performance further. However, limitations exist: the approach is restricted to quadratic conserved quantities, and the scaling of the method to more complex systems is still an active area of research. Despite these limitations, this novel use of Noether’s theorem presents a significant advance in the intersection of physics-informed machine learning and Bayesian model selection.
Bayesian Symmetry#
Bayesian approaches to symmetry detection offer a powerful alternative to classical methods. Instead of imposing symmetries a priori, Bayesian methods learn symmetries from data, using the data to inform the prior distribution over possible symmetries. This is particularly appealing when the true symmetries of a system are unknown or complex. A Bayesian framework allows for quantifying uncertainty in the identified symmetries through posterior distributions. This uncertainty quantification is crucial as it acknowledges that the observed data may be imperfect or incomplete, and thus the inferred symmetries might only be approximate. By incorporating prior knowledge about likely symmetries, Bayesian methods can guide the learning process and reduce overfitting, while simultaneously learning the strength of the symmetry from the data. The use of model selection techniques within the Bayesian framework (e.g., marginal likelihood maximization) can assist in automatically choosing the model complexity appropriate for the observed data, effectively acting as an Occam’s razor in identifying the most parsimonious representation that balances fit with complexity. This combines inductive bias with data-driven learning, making them particularly useful for complex systems where classical methods struggle.
Variational Inference#
Variational inference (VI) is a powerful approximation technique for Bayesian inference, particularly useful when dealing with intractable posterior distributions. VI frames Bayesian inference as an optimization problem, where a simpler, tractable distribution (the variational distribution) is chosen to approximate the true posterior. This approximation is optimized by minimizing a divergence measure, often the Kullback-Leibler (KL) divergence, between the variational distribution and the true posterior. The core idea is to find the variational distribution that is closest to the true posterior, allowing for approximate posterior computations such as calculating moments or sampling. A key advantage is scalability: VI can handle high-dimensional data and complex models, where exact inference methods become computationally infeasible. However, the accuracy of VI depends heavily on the choice of the variational family; a poorly chosen family might result in a poor approximation and inaccurate inferences. Furthermore, the optimization process in VI can be challenging, requiring careful selection of hyperparameters and potentially getting stuck in local optima. Despite these limitations, VI remains a prominent and versatile technique in various applications, including machine learning, probabilistic modeling, and Bayesian statistics, offering a balance between accuracy and computational efficiency.
Hamiltonian Learning#
Hamiltonian learning leverages principles of Hamiltonian mechanics to model dynamical systems. Key to this approach is the representation of the system’s energy (Hamiltonian) as a neural network, allowing for learning from data while respecting fundamental physical constraints. This contrasts with standard neural network approaches which may not guarantee energy conservation or other physical properties. A major advantage is improved generalization and predictive accuracy, especially for long-term predictions, as the learned dynamics are inherently consistent with the laws of physics. However, challenges include efficiently learning complex Hamiltonians from potentially noisy or incomplete data, as well as handling high-dimensional systems. Furthermore, choosing appropriate neural network architectures and loss functions is critical for successful learning. Research in this area is actively exploring ways to incorporate symmetries and conserved quantities to further enhance learning efficiency and generalization.
Symmetry Discovery#
The concept of ‘Symmetry Discovery’ within the context of the provided research paper centers around the automated identification of conserved quantities and their associated symmetries directly from data, bypassing the need for manual specification. This is achieved through a novel application of Noether’s theorem, which elegantly connects symmetries with conserved quantities in Hamiltonian systems. The approach uses a Bayesian model selection framework, enabling the model to automatically favor the simplest (most parsimonious) yet effective symmetry that explains the data, effectively implementing Occam’s Razor. A crucial aspect is the parameterization of symmetries as learnable conserved quantities, directly incorporated into the model’s prior, thus enabling end-to-end learning of both the Hamiltonian and the symmetries. The method leverages a variational lower bound to the marginal likelihood, providing a differentiable objective for optimization. This innovative technique allows the model to simultaneously learn both the Hamiltonian and the conserved quantities from data, demonstrating a practical approach to automated symmetry discovery in complex dynamical systems.
More visual insights#
More on figures

🔼 This figure compares the learned Hamiltonians from three different models on the phase space of a simple harmonic oscillator. The first model is a vanilla Hamiltonian Neural Network (HNN). The second model incorporates the proposed symmetry learning method, while the third model uses the correct SO(2) symmetry as an oracle. The final image shows the true Hamiltonian. This visualization helps to understand how each model learns and represents the inherent symmetry of the system, highlighting the impact of the proposed method in learning the rotational symmetry from data.
read the caption
Figure 2: Learned Hamiltonians on phase space of simple harmonic oscillator by HNN models.
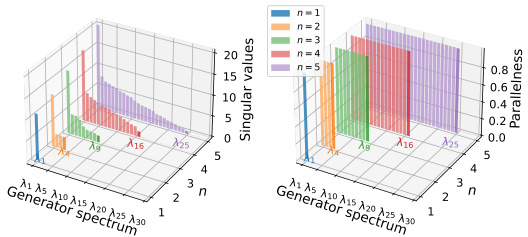
🔼 This figure shows two plots. The left plot displays the singular values of the learned generators for different values of n (number of oscillators). The right plot shows the parallelness (a measure of how closely the learned generators align with the ground truth generators) for each of the learned generators. The plots demonstrate that as n increases, the method correctly learns the U(n) symmetry group, indicated by the presence of n² non-zero singular values and high parallelness values for the corresponding generators. This provides strong visual evidence supporting the paper’s claim of successful automatic symmetry discovery for n-harmonic oscillators.
read the caption
Figure 3: Singular value and parallelness of the singular vectors of the learned generators, for n oscilators. U(n) is correctly learned.
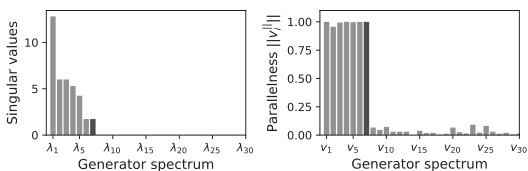
🔼 This figure shows the results of analyzing the learned symmetries for n-harmonic oscillators. The left panel displays the singular values of the learned generators, demonstrating that there are n² non-zero singular values, consistent with the U(n) symmetry group’s dimensionality. The right panel shows the parallelness (the cosine similarity) of the first n² right singular vectors with the ground truth generators. The high parallelness values (close to 1) confirm that the learned generators effectively span the same subspace as the true generators, indicating successful learning of the U(n) symmetry.
read the caption
Figure 3: Singular value and parallelness of the singular vectors of the learned generators, for n oscilators. U(n) is correctly learned.
More on tables

🔼 This table presents the results of an experiment comparing three different Hamiltonian Neural Networks (HNNs) on a 3-fold harmonic oscillator system. The first HNN is a vanilla model without any explicit symmetry constraints. The second HNN incorporates the authors’ symmetry learning method. The third HNN uses the known correct U(3) symmetry as a fixed reference. The table shows that the symmetry learning method achieves comparable performance to the reference model, and significantly outperforms the vanilla model in terms of both ELBO (a measure of model fit) and test MSE (mean squared error on test data). This demonstrates the effectiveness of the proposed symmetry learning approach in improving both model fit and generalization.
read the caption
Table 2: Learning Hamiltonian dynamics of 3-fold harmonic oscillators. We compare HNN with symmetry learning to a vanilla HNN without symmetry learning and to the correct U(3) symmetry built-in as fixed reference oracle. We find that our method can discover the correct symmetry, achieves reference oracle performance, and outperforms vanilla training in both ELBO and test performance.

🔼 This table presents the results of three different Hamiltonian neural network models applied to a 2D 3-body system: a vanilla HNN, an HNN with learned symmetry (the proposed method), and an HNN with the correct SE(2) symmetry built-in as an oracle. The metrics reported are training and test mean squared error (MSE), negative log-likelihood (NLL), Kullback-Leibler divergence (KL), evidence lower bound (-ELBO), and test MSE on three different test sets: the standard test set, a shifted test set, and a wider test set. The results demonstrate that the method with learned symmetry achieves performance comparable to the oracle model, significantly outperforming the vanilla model.
read the caption
Table 3: Learning Hamiltonian dynamics of 2d 3-body system with variational Hamiltonian neural networks (HNN). We compare our symmetry learning method to a vanilla model without symmetry learning and a model with the correct SE(2) symmetry built-in as a reference oracle. Our method capable of discoverying symmetry achieves the oracle performance, outperforming the vanilla method.
Full paper#



















