↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat
TL;DR#
Current methods for 3D surface reconstruction in open scenes face challenges. Neural Radiance Fields (NeRF) methods are slow and require extensive training, while 3D Gaussian Splatting (3DGS) methods, though fast, suffer from high memory usage and can produce rough surfaces. This paper introduces Gaussian Voxel Kernel Functions (GVKF) to overcome these limitations.
GVKF cleverly integrates the speed of 3DGS with the accuracy of implicit representations. It uses kernel regression to create a continuous scene representation from discrete 3DGS data. This allows for high-fidelity surface reconstruction with real-time rendering speed, requiring significantly less memory than previous approaches. The method is shown to be effective in experiments on challenging datasets.
Key Takeaways#
Why does it matter?#
This paper is important because it offers a novel solution to the challenge of efficient and high-quality 3D surface reconstruction in open scenes. It presents a significant advance over existing methods by combining the speed of explicit representations with the accuracy of implicit ones. This opens up exciting new avenues for research in autonomous driving, virtual reality, and other applications requiring real-time 3D scene understanding.
Visual Insights#
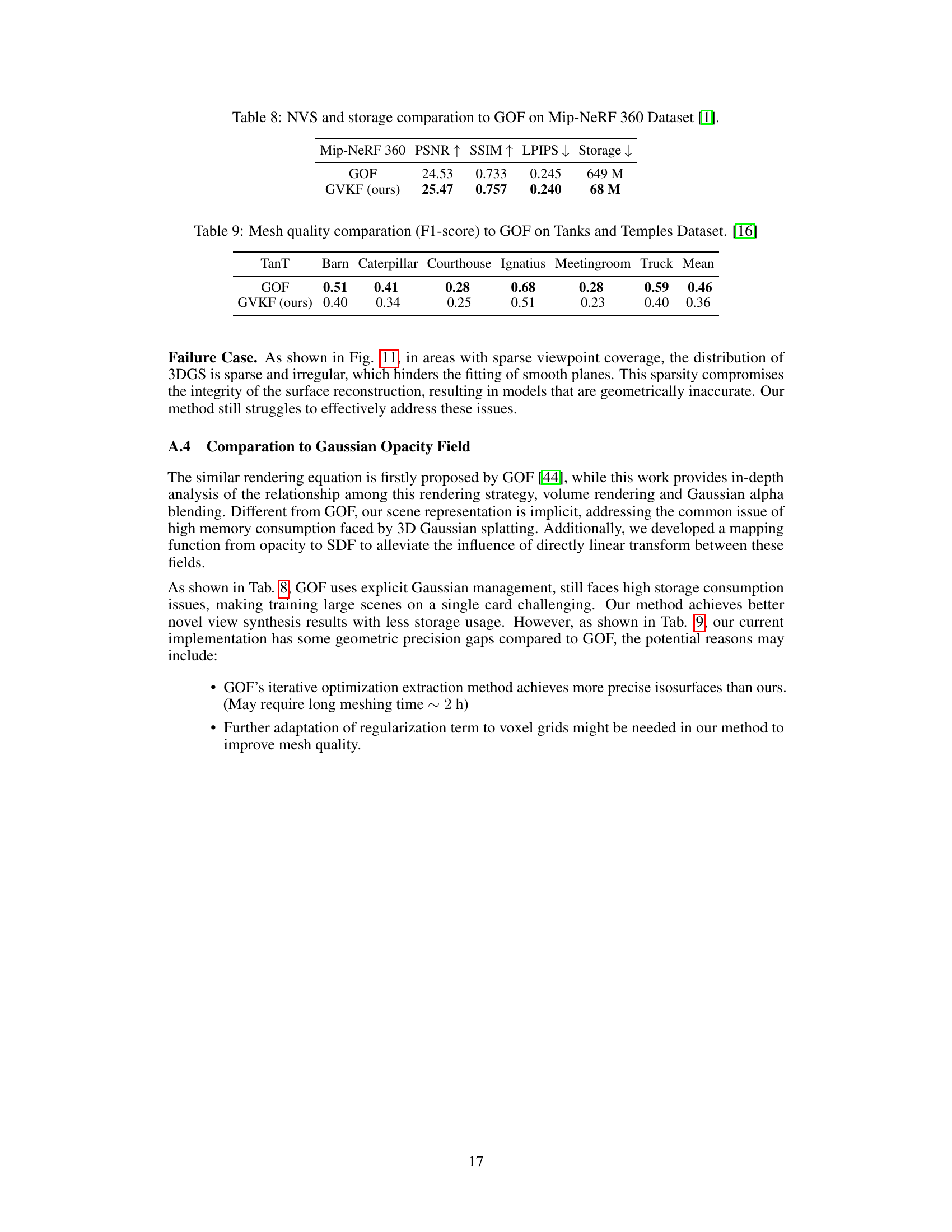
This figure illustrates the framework of the Gaussian Voxel Kernel Functions (GVKF) method. It shows how discrete Gaussian primitives are used to represent a continuous scene opacity density field through kernel regression. The method integrates this with a modified rasterization pipeline and directly maps the resulting neural opacity field to an implicit surface for mesh reconstruction.

This table compares two predominant approaches in 3D surface reconstruction: 3D Gaussian Splatting (3DGS) rendering and volume rendering. It highlights the advantages and disadvantages of each method in terms of mathematical expression, rendering speed, memory consumption, and the quality of 3D surface representation.
In-depth insights#
GVKF: Core Idea#
The core idea behind GVKF is to bridge the gap between the speed of explicit 3D Gaussian splatting (3DGS) and the accuracy of implicit neural radiance fields (NeRF) for 3D surface reconstruction. GVKF leverages the fast rasterization of 3DGS but uses kernel regression to create a continuous scene representation from the discrete Gaussian primitives. This allows for high-fidelity surface reconstruction without the extensive training time of NeRF-based methods. A key innovation is the mathematical integration of Gaussian alpha blending with traditional volume rendering, allowing for a more efficient and effective implicit scene representation. This innovative approach, along with the use of a sparse voxel grid for efficient Gaussian management, results in a method that is both faster and more memory-efficient than existing approaches. The bidirectional mapping between opacity and surface allows for direct mesh extraction, further enhancing the method’s efficiency and utility.
3DGS Enhancement#
The concept of “3DGS Enhancement” in the context of 3D surface reconstruction revolves around improving the efficiency and quality of 3D Gaussian Splatting (3DGS). Standard 3DGS, while offering fast rendering, suffers from high memory consumption and limitations in representing fine surface details, particularly in sparse regions. Enhancements focus on addressing these shortcomings. This might involve optimizing the splatting algorithm itself for speed and memory efficiency, employing advanced data structures for better spatial organization of Gaussian primitives, or integrating techniques like kernel regression to create a continuous scene representation from the discrete Gaussian points. Implicit surface extraction methods could also be incorporated to improve surface quality and reduce reliance on explicit point clouds. The ultimate goal is a method that combines the speed advantages of 3DGS with the higher fidelity of methods such as Neural Radiance Fields (NeRFs), while overcoming the limitations of both approaches. Key areas of exploration include efficient memory management of Gaussian primitives, advanced data structures such as octrees or hash tables, and the development of hybrid implicit-explicit representations that leverage the strengths of both approaches. A successful enhancement would balance computational cost, memory usage, and the fidelity of the resulting 3D model.
Implicit Surface#
The concept of implicit surfaces within the context of 3D reconstruction is crucial for representing complex shapes efficiently. Implicit surface representations define a surface indirectly, unlike explicit methods that use a mesh or point cloud. This indirect approach allows for greater flexibility and ease of manipulation, especially when dealing with evolving or complex shapes, and is particularly advantageous in the context of high-fidelity surface reconstruction in open scenes. The paper leverages this by creating a continuous scene representation built from discrete Gaussian primitives, effectively bridging the gap between explicit and implicit methods. This strategy ensures the benefits of fast rasterization while maintaining the accuracy afforded by continuous surfaces. The success of this approach hinges on the reliable mapping between the implicit surface and the discrete Gaussian representations, a critical aspect demanding careful mathematical treatment and algorithmic design. Accurate and efficient surface reconstruction necessitates a robust algorithm for extracting meshes from this implicit representation. The paper’s success is partially determined by how effectively this extraction is performed.
Open Scene Tests#
In evaluating a 3D surface reconstruction model’s performance in open scenes, a rigorous testing methodology is crucial. Open scene tests would ideally encompass diverse, complex environments, not just controlled lab settings. The tests must assess the accuracy and efficiency of the reconstruction across varying scene complexities, including variations in object density, occlusions, lighting conditions, and the presence of dynamic elements. Quantitative metrics such as PSNR, SSIM, and Chamfer distance should be employed to evaluate reconstruction accuracy. Qualitative analysis of the reconstructed surfaces is also vital, considering factors like visual fidelity, geometric detail, and the handling of fine details in challenging areas. Real-time performance is another important aspect in open scenes, as the speed of reconstruction is critical for practical applications. Finally, it is also important to consider memory and computational resource consumption as key factors when evaluating the model in open scenes.
GVKF Limitations#
The Gaussian Voxel Kernel Functions (GVKF) method, while promising for efficient 3D surface reconstruction in open scenes, presents some limitations. Local fitting of SDFs, unlike global approaches used in NeRF-based methods, hinders the accuracy in areas with sparse viewpoints, leading to uneven surfaces. The dependence on 3D Gaussian splatting, while enabling fast rasterization, inherently struggles with irregular or sparse Gaussian distributions, impacting surface quality in challenging scenes. Although GVKF aims for real-time rendering, achieving this might require optimization compromises in certain aspects of the reconstruction quality. The handling of dynamic elements and complex scenes remains underdeveloped, indicating a potential drawback in practical applications involving movement or cluttered environments. Finally, while a mapping is derived from opacity to the surface, the process involves a transcendental equation, potentially adding computational complexity.
More visual insights#
More on figures
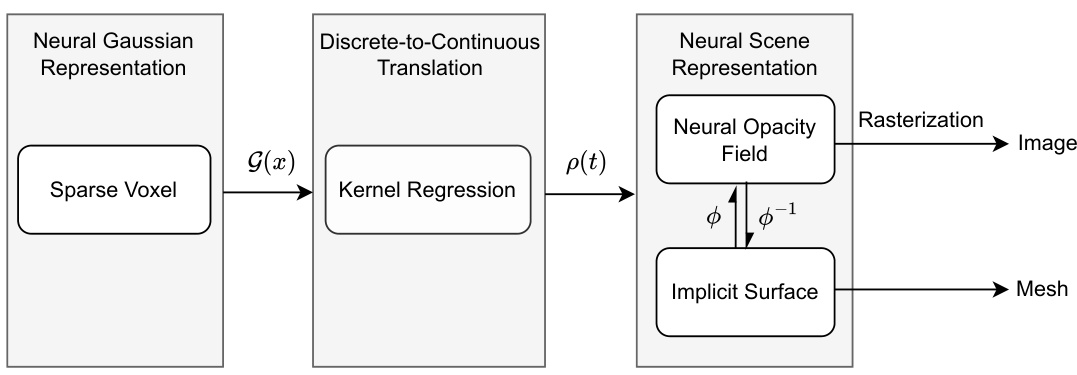
This figure compares three different rendering methods: volume rendering, 3D Gaussian splatting with alpha blending, and the proposed GVKF rendering. It illustrates how each method represents the opacity density function p(t) along a ray. Volume rendering uses a continuous representation. 3D Gaussian splatting uses discrete Gaussians, leading to a discontinuous opacity function. GVKF combines the speed of 3DGS rasterization with a continuous opacity representation via kernel regression, creating a smoother, more accurate representation.
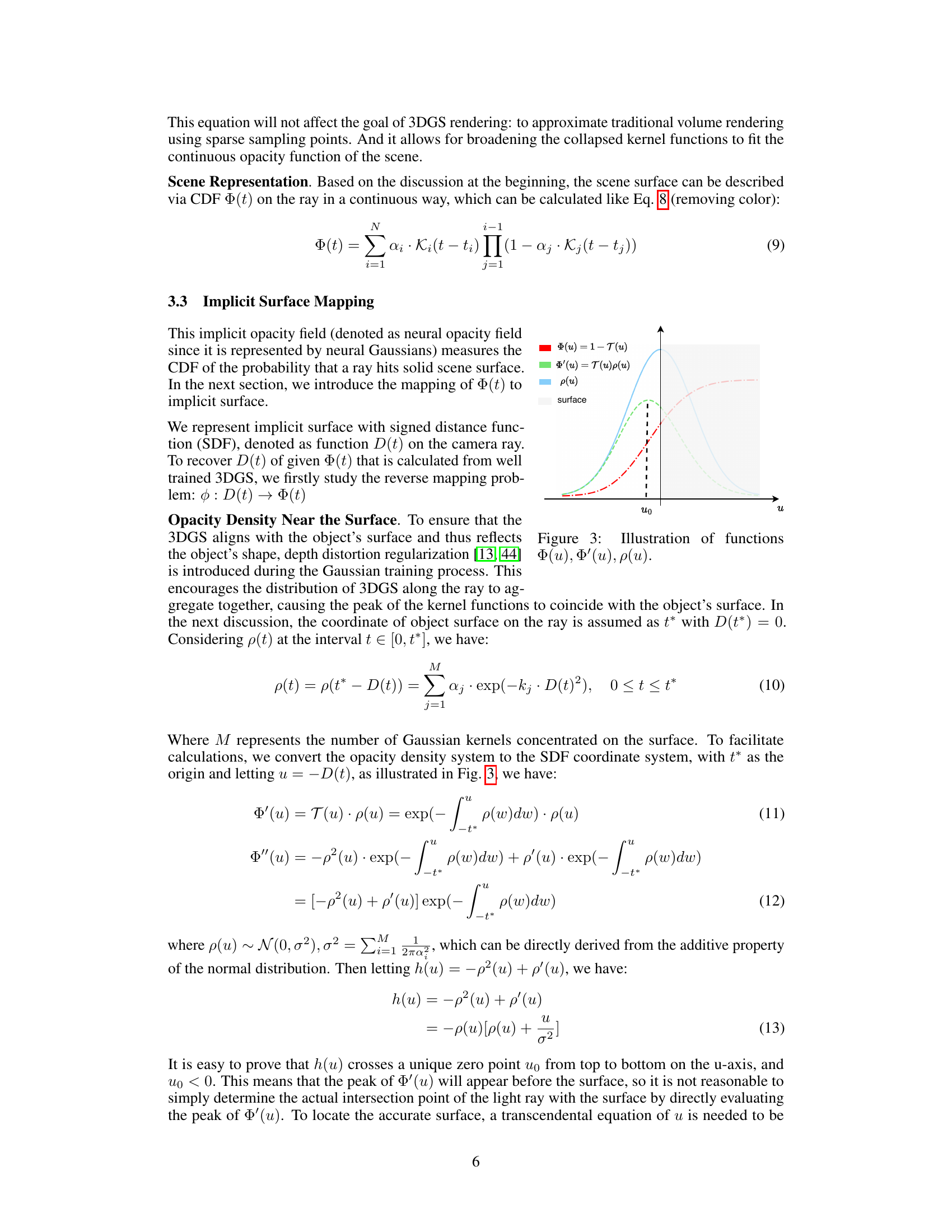
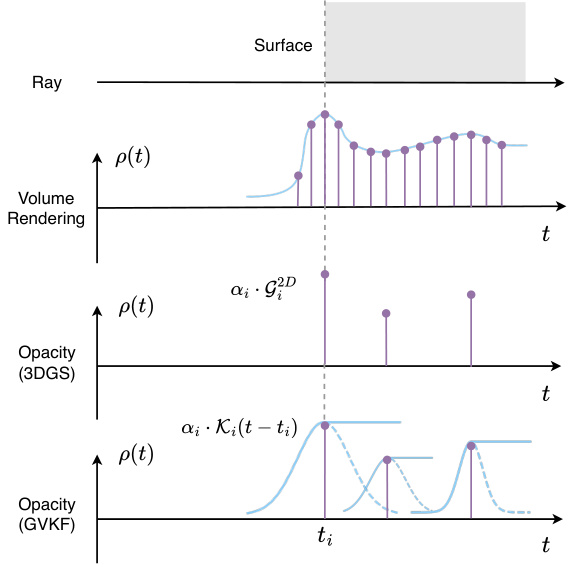
This figure illustrates the relationship between three functions: Φ(u), Φ’(u), and p(u), which are crucial for understanding the implicit surface mapping in the GVKF method. Φ(u) represents the cumulative distribution function (CDF) of the probability that a ray hits a particle. Φ’(u) represents the probability density function (PDF), showing the probability of a ray encountering a particle at a specific point. p(u) is the opacity density function, indicating the probability of a ray being blocked at a given point. The dashed black line represents the location of the surface (where D(t*) = 0). The figure demonstrates how the peak of Φ’(u) precedes the actual surface location, highlighting the need for a more sophisticated method (using Logistic Function) to accurately map from the opacity density to the surface location.

This figure compares the results of novel view synthesis and surface reconstruction on the Waymo Open Dataset between the proposed GVKF method and two other methods (StreetSurf and 2DGS). Each row shows the ground truth image alongside the results from the three different methods for a different scene. PSNR (Peak Signal-to-Noise Ratio) values are included to quantify the image quality of the reconstruction. The results suggest that the GVKF method outperforms the others in terms of geometric accuracy and detail, particularly in open scenes.
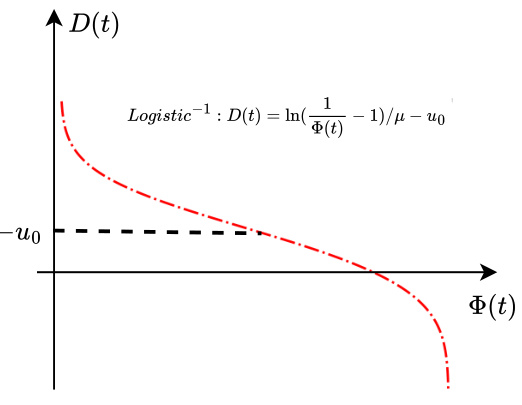
This figure illustrates the relationship between the opacity density function p(u), the cumulative distribution function Φ(u), and its derivative Φ’(u) near the surface of an object. The x-axis represents the distance u (negative signed distance from the surface), and the y-axis represents the values of these functions. The peak of Φ’(u) indicates the most likely location of the surface along the ray, while Φ(u) represents the cumulative probability of a ray hitting the surface up to distance u. The function p(u) depicts the opacity density at a given distance from the surface.

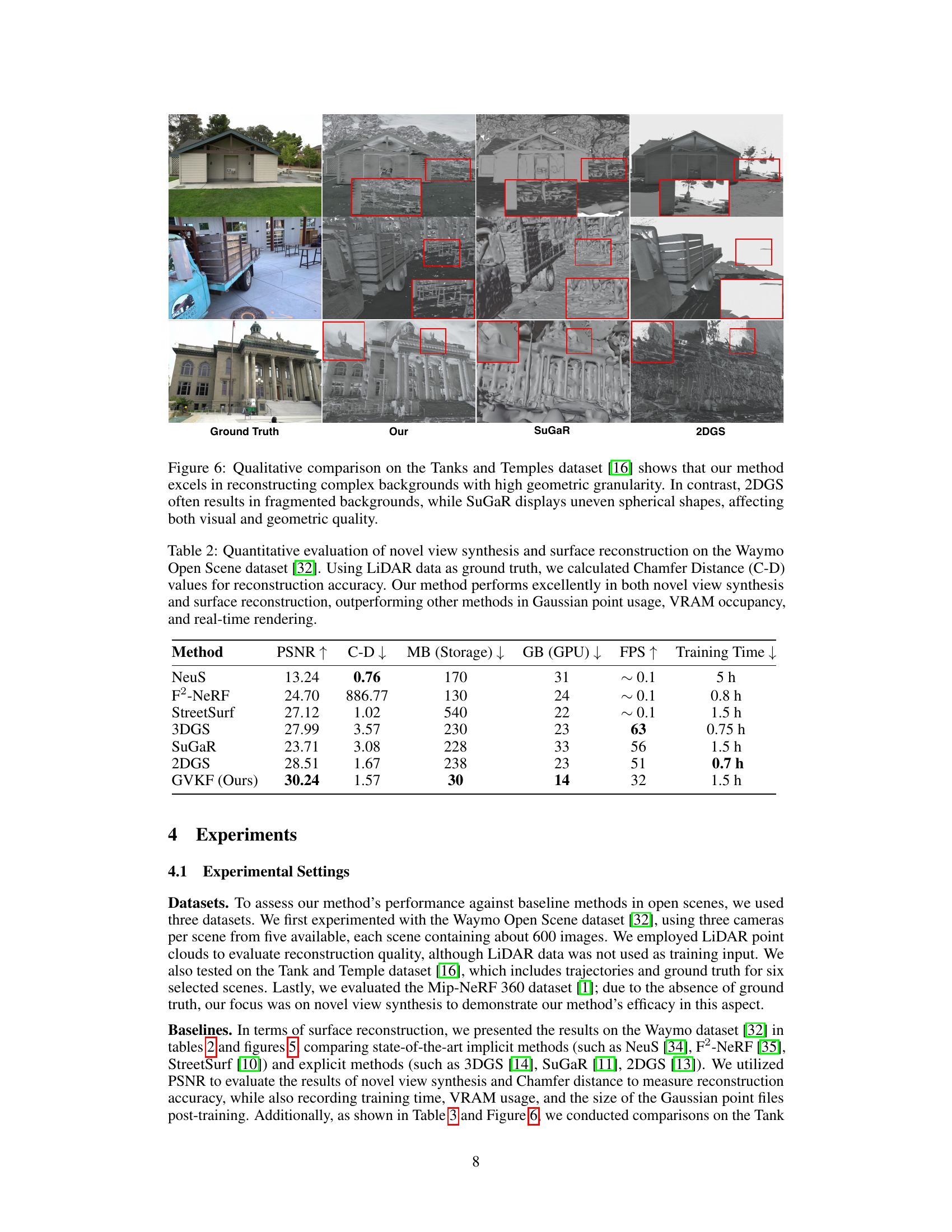
This figure compares the qualitative results of surface reconstruction on the Tanks and Temples dataset between the proposed GVKF method and other existing methods (SuGaR and 2DGS). The results show that GVKF outperforms other methods by having higher geometric granularity and reconstructing more complex backgrounds, while SuGaR and 2DGS produce fragmented backgrounds and uneven spherical shapes. The red boxes highlight areas where the difference is prominent.
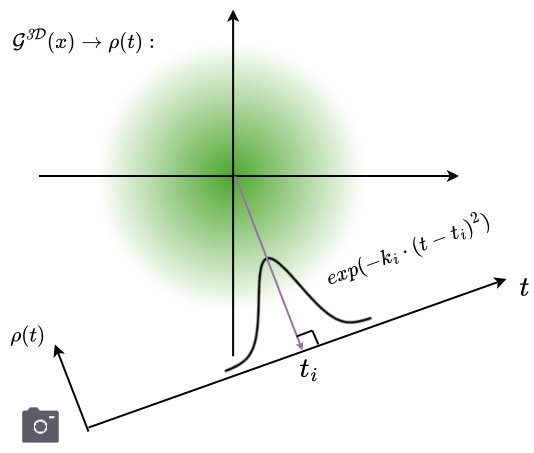
This figure illustrates the transformation of a 3D Gaussian primitive G(x) into a 1D Gaussian function p(t) along a ray. The 3D Gaussian is projected onto a line (the ray), resulting in a 1D Gaussian distribution with its peak at t_i representing the point of maximum impact of the 3D Gaussian on that specific ray. The formula and derivation of this transformation are mathematically explained in the paper.

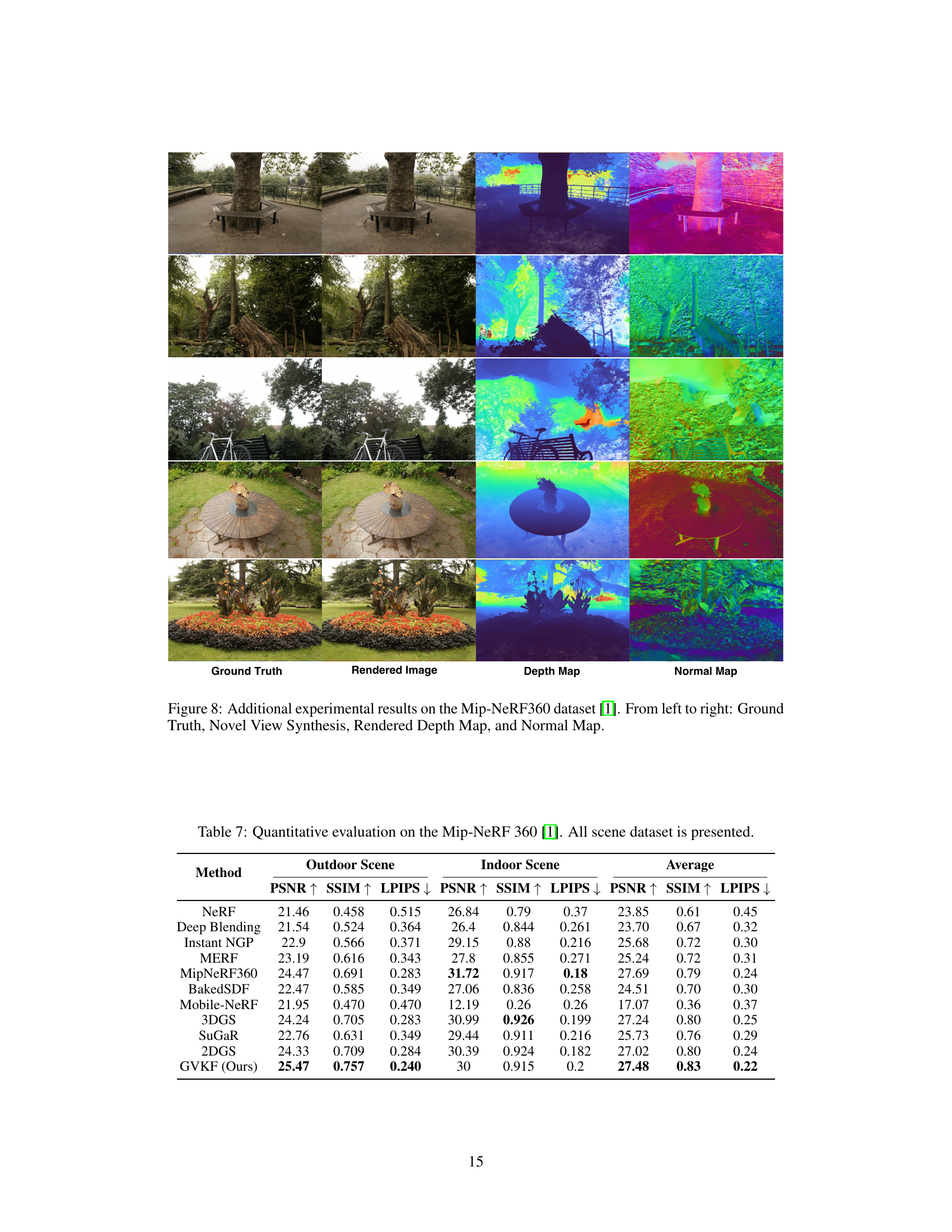
This figure shows a qualitative comparison of the proposed GVKF method with ground truth data on the Mip-NeRF360 dataset. For several scenes, it displays the ground truth image alongside a rendered image produced by the GVKF method. It also shows the depth map and normal map generated by GVKF for each scene. This allows for a visual assessment of the accuracy and quality of the method’s reconstruction in terms of geometry, depth, and surface normals.

This figure presents a qualitative comparison of the proposed GVKF method with ground truth data on the Mip-NeRF360 dataset. It shows several example scenes where the method was tested, with the ground truth, novel view synthesis results, depth maps, and normal maps presented side-by-side for each scene. This allows for a visual assessment of the accuracy and quality of the surface reconstruction and novel view synthesis achieved by the GVKF method.
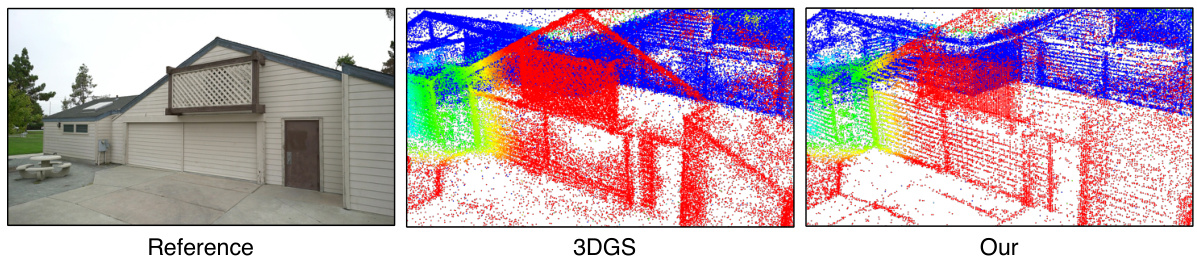
This figure compares the Gaussian point visualization of the proposed GVKF method with that of the traditional 3DGS method. The reference image shows a clear, detailed view of the scene. The 3DGS visualization shows a scattered distribution of Gaussian points with some areas appearing denser than others. In contrast, the GVKF visualization demonstrates a more even and organized distribution of Gaussian points, leading to a smoother and more coherent representation of the scene’s geometry. This highlights the effectiveness of the GVKF method in efficiently managing and representing Gaussian primitives for 3D surface reconstruction.

This figure shows a failure case of the GVKF method where a sparse view area results in an uneven surface due to insufficient Gaussian points to represent the surface details accurately. It highlights a limitation of the approach when dealing with scenes where some areas have limited view coverage.
More on tables
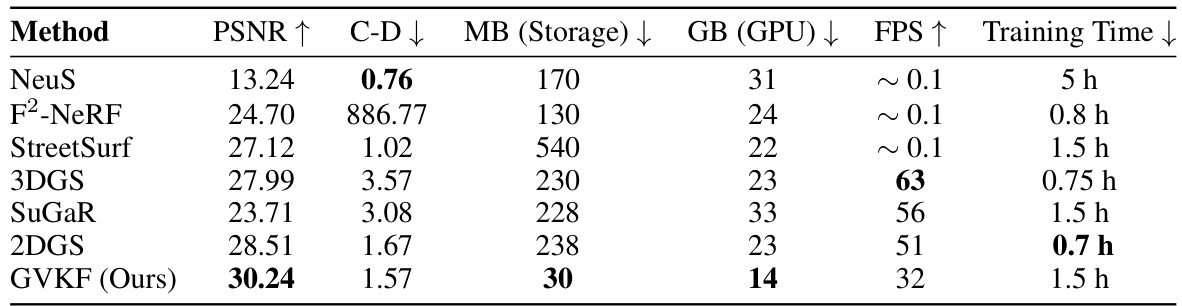
This table presents a quantitative comparison of different methods for novel view synthesis and surface reconstruction on the Waymo Open Scene dataset. The metrics used include PSNR (peak signal-to-noise ratio), Chamfer Distance (a measure of geometric reconstruction error), memory usage (MB), GPU memory usage (GB), frames per second (FPS), and training time. The results show that the proposed GVKF method outperforms existing state-of-the-art methods in terms of PSNR, Chamfer Distance, memory and GPU usage and rendering speed.
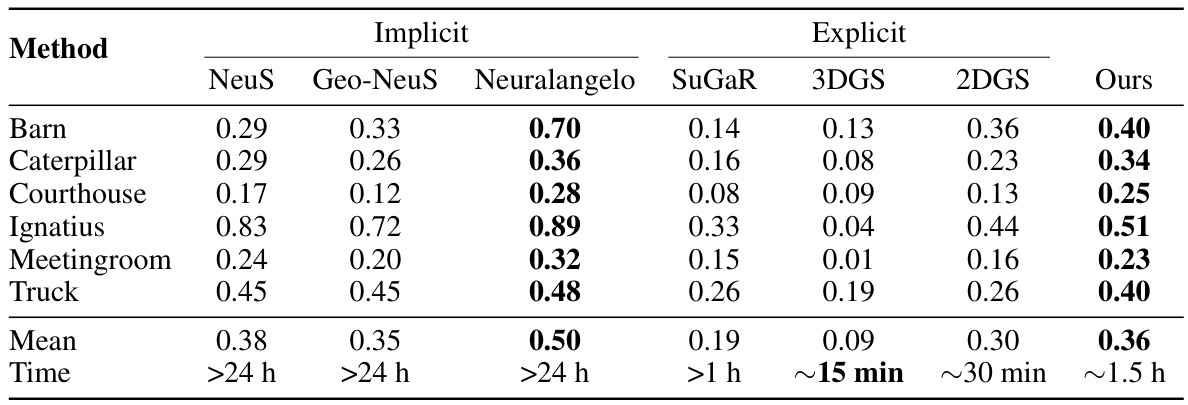
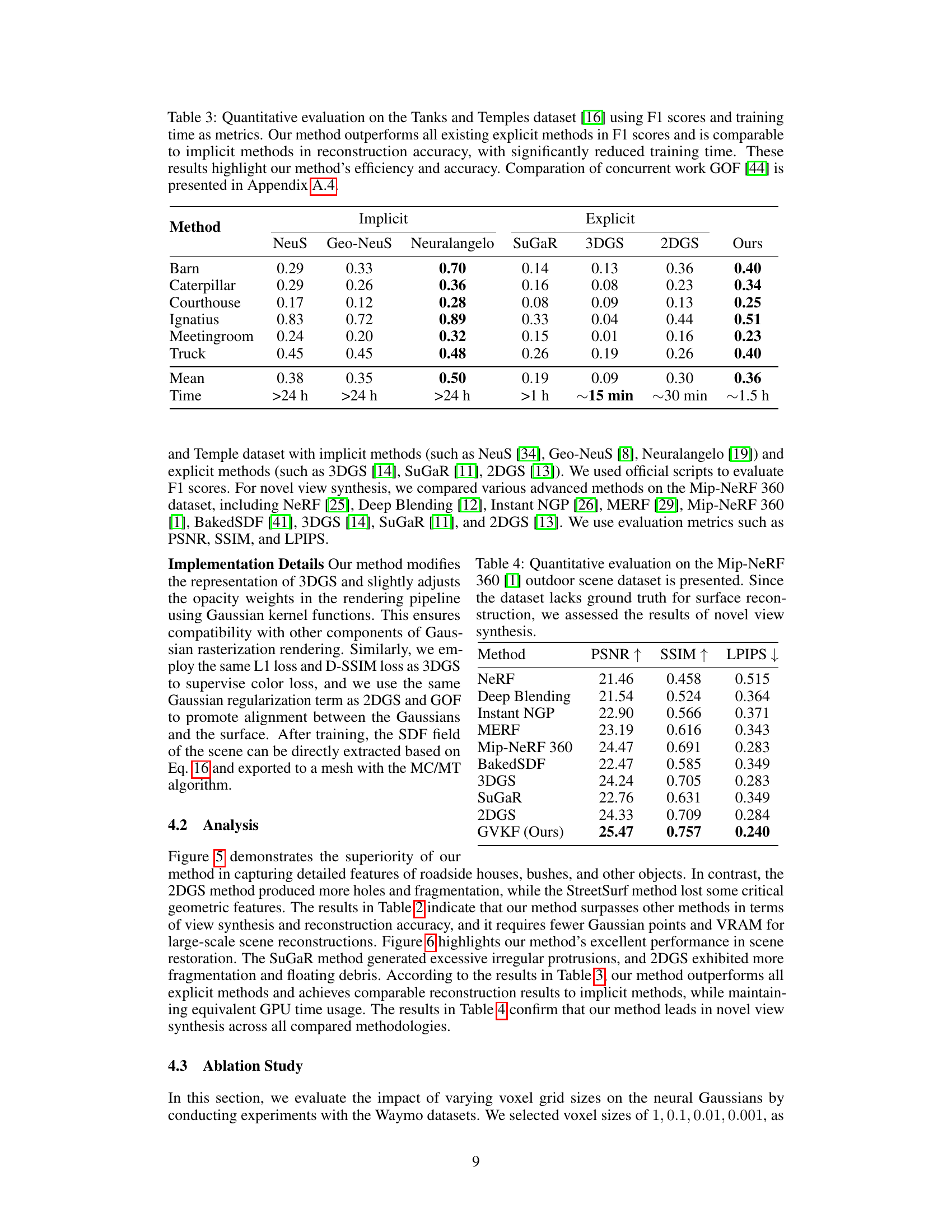
This table presents a quantitative comparison of different methods (both implicit and explicit) for 3D surface reconstruction on the Tanks and Temples dataset. The metrics used are F1 scores and training time. The results show that the proposed method outperforms existing explicit methods in terms of F1 scores and has comparable accuracy to implicit methods while significantly reducing training time.
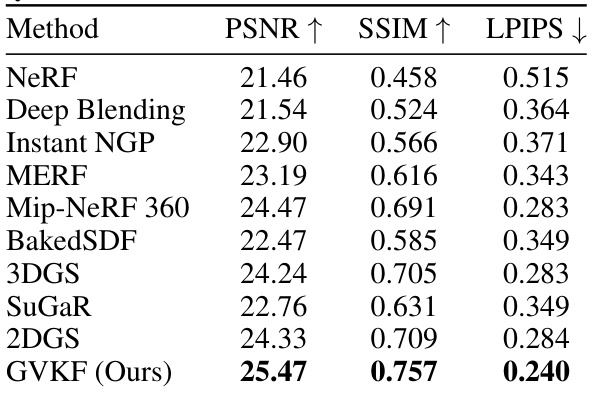
This table presents a quantitative comparison of different novel view synthesis methods on the Mip-NeRF 360 dataset. The metrics used for comparison are PSNR (higher is better), SSIM (higher is better), and LPIPS (lower is better), providing a comprehensive assessment of the visual quality of the generated novel views. The results are averaged across all scenes in the dataset.

This table presents the results of an ablation study on the GVKF method. The study investigates the impact of removing the voxel grid and the SDF mapping on the performance of the method, measured by PSNR, F1 score, memory usage, storage, training time and meshing time. The results show that using both voxel grid and SDF mapping is beneficial for the performance of the method.
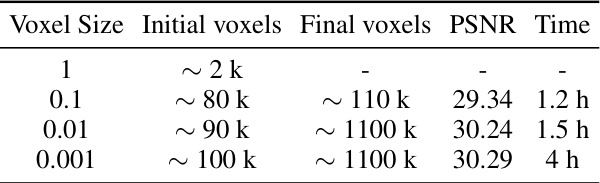
This table presents the results of an ablation study on the effect of varying voxel grid sizes on the neural Gaussians. It shows the initial number of voxels, the final number of voxels after training, the peak signal-to-noise ratio (PSNR), and the training time for different voxel sizes (1, 0.1, 0.01, and 0.001). The data demonstrates the trade-off between training time and PSNR as the voxel size is reduced.
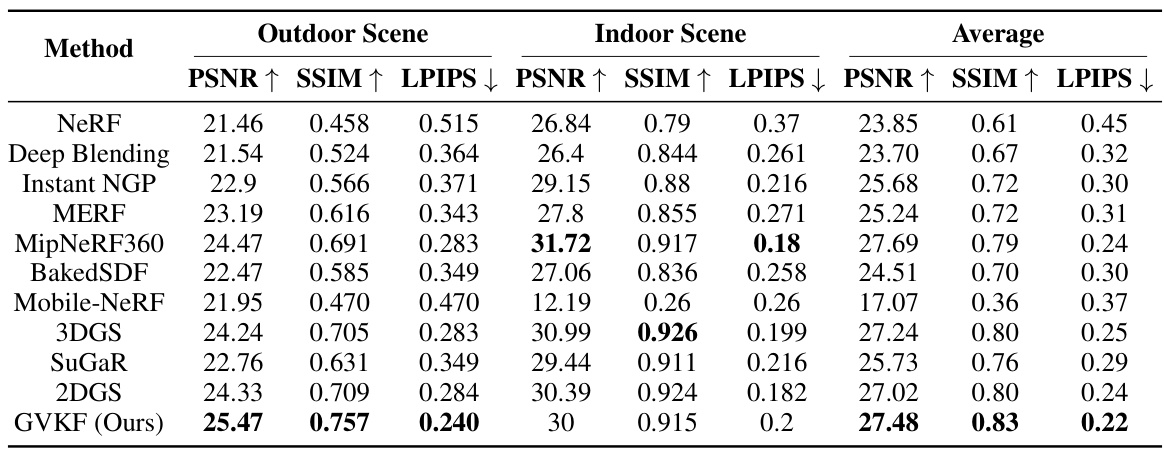
This table presents a quantitative comparison of different methods for novel view synthesis and surface reconstruction using the Waymo Open Scene dataset. The metrics used are PSNR (Peak Signal-to-Noise Ratio), Chamfer Distance (C-D), memory usage (MB), GPU memory usage (GB), Frames Per Second (FPS), and training time. LiDAR data serves as the ground truth for evaluating reconstruction accuracy. The results demonstrate the superior performance of the proposed GVKF method in terms of PSNR, reduced Chamfer distance, lower memory consumption, higher FPS, and comparable training time.
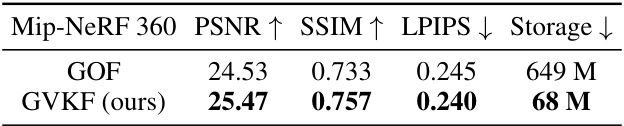
This table compares the performance of the proposed GVKF method with the GOF method on the Mip-NeRF 360 dataset in terms of novel view synthesis (NVS) quality and storage requirements. The metrics used are PSNR (peak signal-to-noise ratio), SSIM (structural similarity index), LPIPS (learned perceptual image patch similarity), and storage size (in megabytes). Higher PSNR and SSIM values indicate better image quality, while lower LPIPS values and smaller storage sizes represent improved performance.

This table presents a quantitative comparison of the proposed GVKF method against several existing implicit and explicit methods for 3D surface reconstruction on the Tanks and Temples dataset. The comparison focuses on F1 scores (a measure of reconstruction accuracy) and training time. The results show that GVKF outperforms explicit methods in terms of F1 score and is competitive with implicit methods while requiring significantly less training time. A comparison to the concurrent work GOF [44] is available in the appendix.
Full paper#