↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current graph learning methods struggle with catastrophic forgetting when handling new data, especially in few-shot scenarios where labeled data is limited. Existing solutions often rely on extensive memory and computationally expensive fine-tuning, which hinder efficiency and scalability. This paper tackles these issues.
The proposed method, Mecoin, uses a novel memory module to efficiently store and update class prototypes. This addresses catastrophic forgetting by separating class prototype learning and node probability distribution learning. Experiments show Mecoin’s significant performance gains over existing methods in accuracy and reduced forgetting rate, demonstrating its practical value in real-world applications with limited resources.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in graph learning and continual learning. It directly addresses the challenge of catastrophic forgetting in dynamic graph settings, a significant hurdle limiting real-world applications. By proposing an efficient memory module, it offers a practical solution with superior performance compared to existing methods. This opens up new avenues for research, particularly in few-shot incremental learning scenarios where data is scarce, improving the applicability of graph neural networks in evolving systems.
Visual Insights#
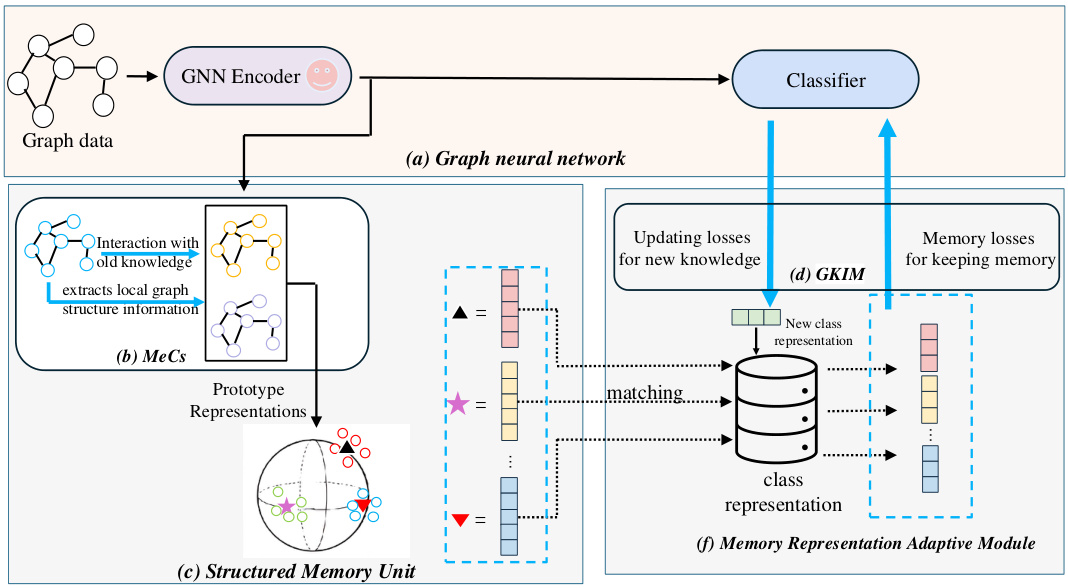
This figure shows the architecture of the Mecoin framework for graph few-shot class-incremental learning (GFSCIL). It consists of three main modules: a graph neural network (GNN) encoder and classifier, a structured memory unit (SMU), and a memory representation adaptive module (MRaM). The GNN processes the graph data, while the SMU maintains and updates class prototypes using the Memory Construction Module (MeCs). The MRaM facilitates adaptive knowledge interaction with the GNN through the Graph Knowledge Interaction Module (GKIM), allowing the model to learn from limited samples and retain prior knowledge.
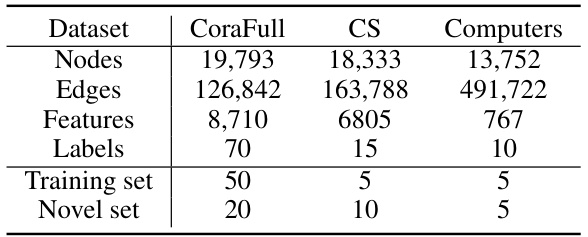
This table presents the characteristics of three real-world graph datasets used in the experiments: CoraFull, CS, and Computers. For each dataset, it shows the number of nodes, edges, features (attributes of the nodes), labels (classes), the size of the training set used for the initial GNN pre-training, and the size of the novel set used for the incremental few-shot learning experiments. The split of the datasets into training and novel sets reflects the setup for continual learning.
In-depth insights#
Memory Module Design#
Designing an effective memory module for continual learning in graph neural networks is crucial for mitigating catastrophic forgetting. A well-designed module should efficiently store and retrieve relevant information, ideally with minimal memory footprint and computational overhead. Structured Memory Units (SMUs) offer an elegant approach by organizing memory into meaningful structures, perhaps using prototypes to represent learned classes. This allows for efficient updating of class prototypes with new data and improves knowledge retention. However, simply caching prototypes isn’t sufficient. Mechanisms to manage interactions between new information and stored prototypes are essential. Memory Construction Modules (MCMs), for example, can leverage self-attention mechanisms to guide these interactions, emphasizing pertinent information. Furthermore, Memory Representation Adaptation Modules (MRAMs) might improve efficiency by decoupling prototype learning from parameter fine-tuning. This approach could store class probabilities separately and dynamically update them, reducing the need for extensive parameter adjustments that can lead to catastrophic forgetting. The key lies in finding the optimal balance between memory capacity and computational efficiency while minimizing forgetting.
Catastrophic Forgetting#
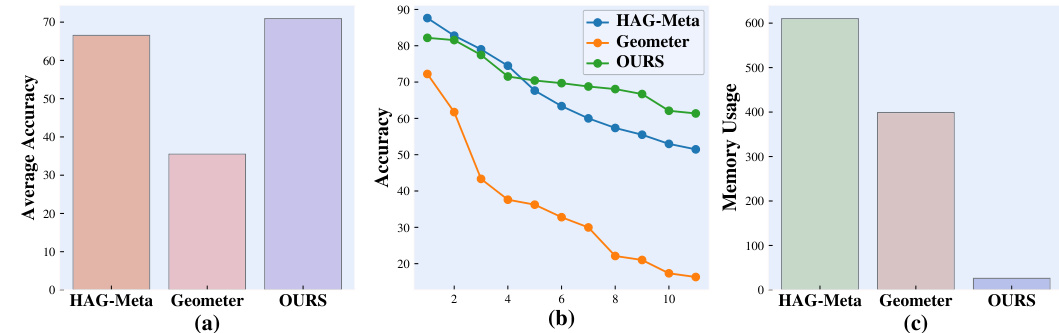
Catastrophic forgetting, a significant challenge in incremental learning, is the tendency of neural networks to rapidly forget previously learned knowledge when adapting to new tasks. In the context of graph few-shot class-incremental learning (GFSCIL), this problem is amplified by the scarcity of labeled data for new classes. Traditional methods often address this by storing large amounts of data, leading to high memory consumption. However, efficient memory mechanisms are crucial to enable GFSCIL while mitigating forgetting. The paper addresses this by proposing a novel memory module that focuses on maintaining class prototypes efficiently through structured memory units and memory representation adaptation, thereby reducing the need for extensive parameter fine-tuning that contributes to forgetting. The key innovation lies in separating class prototype learning from probability distribution learning. This allows the model to maintain knowledge of past categories effectively even while adapting to new ones. The approach demonstrates significant improvements in accuracy and retention compared to state-of-the-art methods, highlighting the effectiveness of addressing catastrophic forgetting through memory management techniques specialized for the unique characteristics of GFSCIL.
GFSCIL Experiments#
In the hypothetical “GFSCIL Experiments” section, a robust evaluation of the proposed Mecoin framework would be crucial. This would necessitate a multifaceted experimental design, likely involving multiple real-world graph datasets exhibiting varying characteristics in terms of size, node/edge density, and label distribution. Baselines would need careful selection, encompassing state-of-the-art methods in graph few-shot class-incremental learning (GFSCIL) such as those using regularization, memory replay, or prototype-based approaches. Metrics should go beyond simple accuracy, incorporating measures of catastrophic forgetting and memory efficiency. The results should be presented in a clear, concise manner, possibly using tables and figures that effectively visualize performance across different sessions and datasets. Statistical significance testing would be important to validate the observed improvements. Furthermore, an ablation study would strengthen the claims by systematically evaluating the impact of each component of Mecoin (SMU, MRaM, GKIM), demonstrating their individual contributions and synergistic effects. Finally, a discussion comparing the results to baselines should be included, along with an analysis of the limitations and potential areas for future work, providing a comprehensive assessment of Mecoin’s effectiveness and potential in GFSCIL scenarios.
Ablation Study#
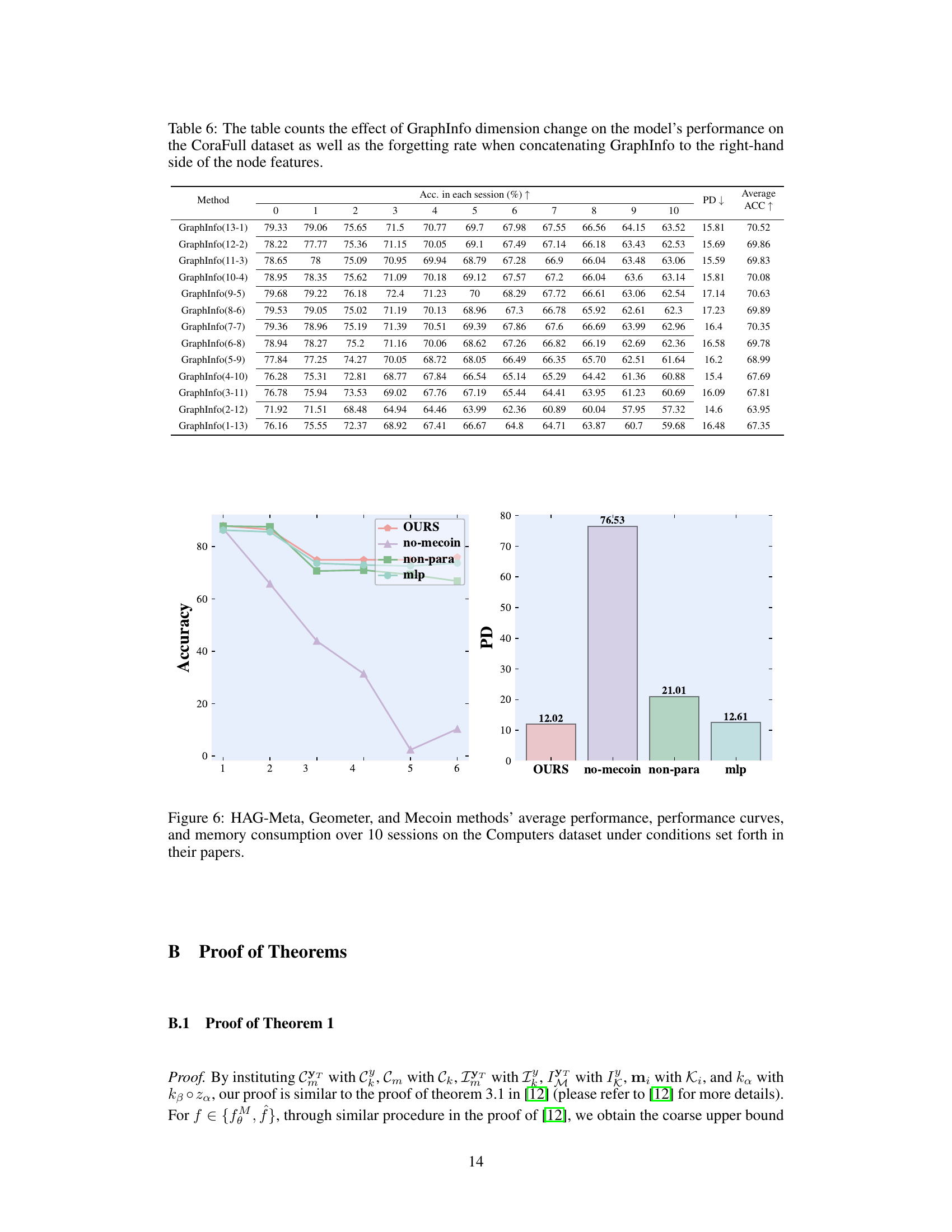
An ablation study systematically removes components of a model to assess their individual contributions. In this context, it would involve evaluating Mecoin’s performance with and without key modules (e.g., the Structured Memory Unit, Memory Representation Adaptive Module, or Graph Knowledge Interaction Module). By isolating each part, the study would quantify the specific impact of each component on metrics like accuracy and forgetting rate. This allows researchers to validate design choices and highlight which aspects are most crucial to Mecoin’s success. For instance, disabling the GraphInfo component would reveal the extent to which local graph structure information contributes to effective prototype learning and memory retention. A thorough ablation study is essential for establishing a comprehensive understanding of Mecoin’s inner workings and its overall effectiveness in few-shot class-incremental learning for graphs. The results can then inform future development and optimization of the method.
Future Directions#
Future research could explore several promising avenues. Improving the efficiency and scalability of Mecoin for handling extremely large graphs is crucial. This might involve exploring more efficient memory structures or incorporating techniques like graph sparsification. Another area of focus is enhancing Mecoin’s ability to handle more complex graph structures, such as those with heterogeneous node types and edge relationships. Furthermore, researchers could investigate different knowledge distillation strategies and the potential for using more sophisticated mechanisms to prevent catastrophic forgetting. Finally, a thorough evaluation on a broader range of datasets with varying characteristics and complexities would strengthen the generalizability and robustness of Mecoin. The effectiveness of Mecoin with limited labeled data in real-world scenarios also warrants further investigation, requiring evaluation on real-world GFSCIL tasks with scarce labeled samples to fully demonstrate its practical application.
More visual insights#
More on figures
This figure illustrates the architecture of the Mecoin framework for Graph Few-Shot Class-Incremental Learning (GFSCIL). It shows the interaction between a Graph Neural Network (GNN), a Structured Memory Unit (SMU), and a Memory Representation Adaptive Module (MRaM). The GNN is pre-trained and its encoder parameters are frozen during GFSCIL. The SMU uses a Memory Construction Module (MeCs) to create and store class prototypes. The MRaM facilitates the interaction between the GNN and the SMU, enabling adaptive knowledge transfer.

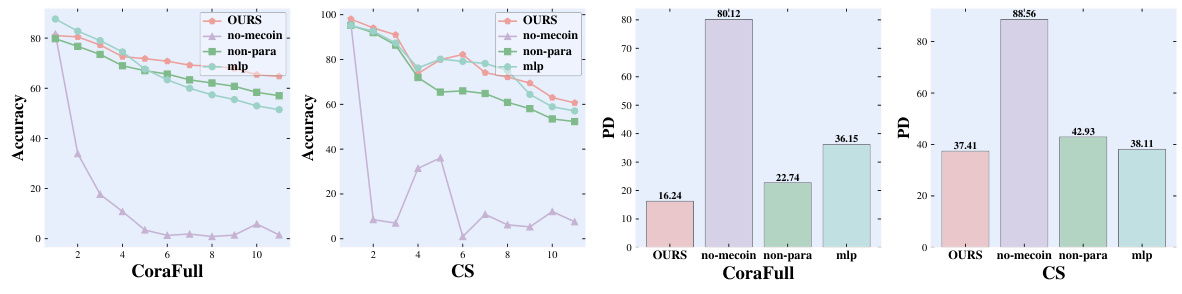
This figure shows the results of ablation experiments on GKIM. Four different scenarios are compared: 1. GKIM with all features enabled. 2. GKIM without node feature interaction with class prototypes in the SMU. 3. GKIM without GraphInfo. 4. GKIM without the MeCs module. The results are shown separately for three different datasets: CoraFull, Computers, and CS. The plots visualize the performance in terms of accuracy and forgetting rate.
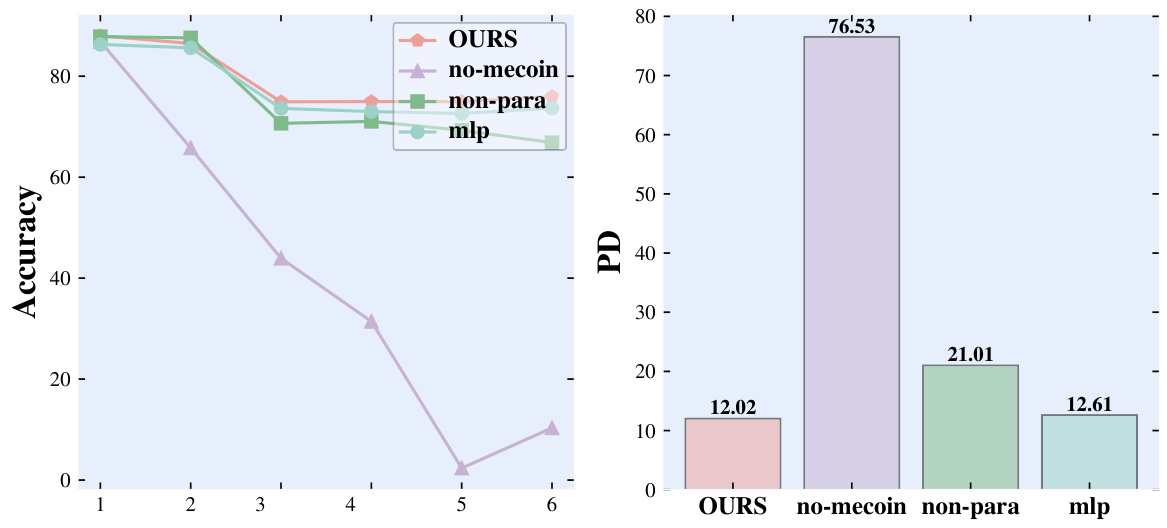
This figure shows the performance and forgetting rates of different methods across multiple sessions on two datasets. The left two columns display line charts illustrating the accuracy of each method over time, while the right two columns present histograms depicting their forgetting rates. The comparison helps to visualize how effectively each method maintains past knowledge while learning new information.
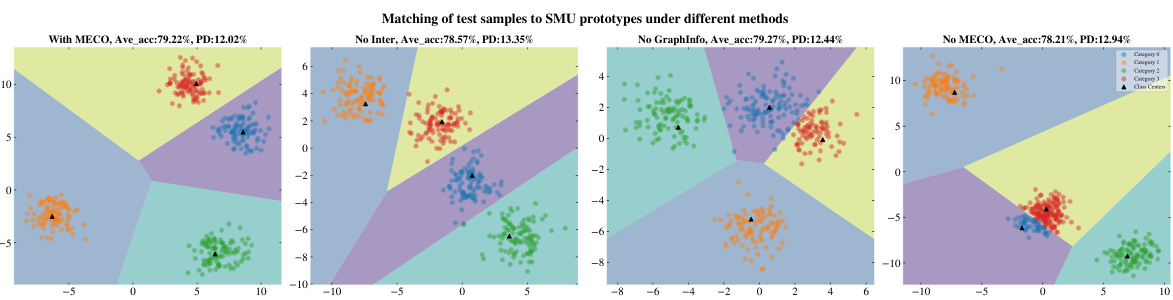
This figure shows the results of an ablation study on the GKIM model for graph few-shot continual learning. Four different versions of the model are tested on the Computers dataset: the full GKIM model, a version without GraphInfo, a version where node features do not interact with class prototypes, and a version without MeCs. The results show that all components contribute to the model’s performance. The visualization displays the clustering of 400 samples from four randomly selected categories, highlighting the differences in prototype representation and class boundary separation among the various model versions.
This figure shows the ablation study results on the performance of GKIM under different configurations. The leftmost column shows the results of GKIM with all features enabled (MeCs, GraphInfo, interaction between node features and class prototypes). Subsequent columns remove one component at a time: no interaction between node features and class prototypes, no GraphInfo, and finally no MeCs. Each row represents results on a different dataset (CoraFull, Computers, CS). The plots visualize the resulting accuracy and forgetting rate (PD) for each session.
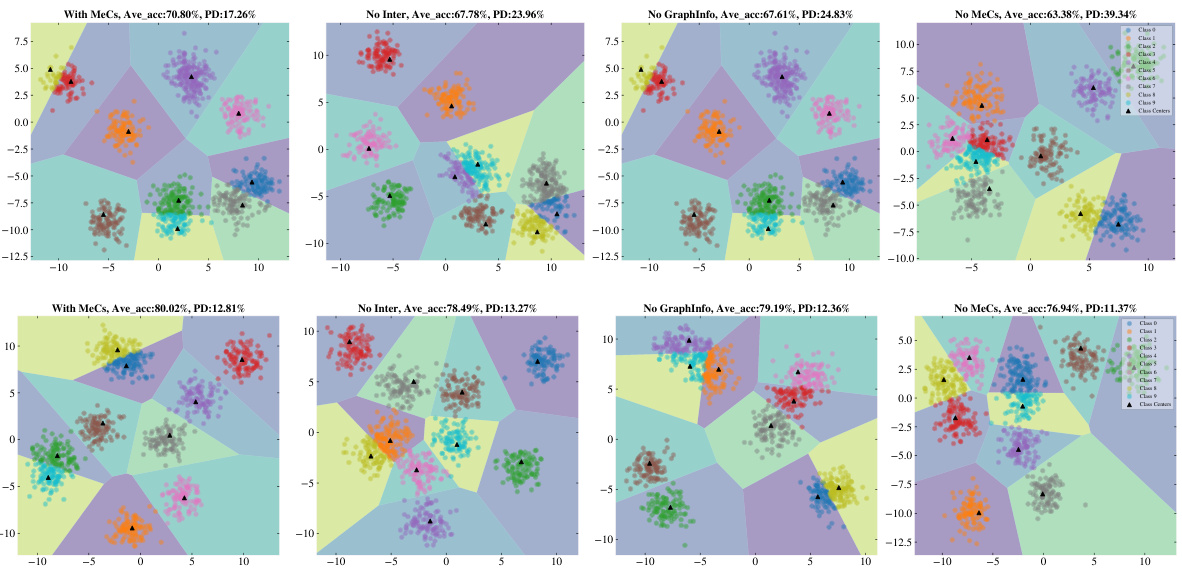
This figure shows the ablation study results of the GKIM module in the Mecoin framework. It presents four variations of the GKIM’s performance across three datasets (CoraFull, Computers, CS) under different conditions. The four conditions tested are: GKIM with all features enabled, GKIM without interaction between node features and class prototypes (No Inter), GKIM without local graph structure information (No GraphInfo), and GKIM without the Memory Construction Module (MeCs, which is renamed from MeCo in the original paper). The results are visualized in a two-dimensional space, illustrating differences in accuracy and forgetting rate across these conditions.

This figure shows the results of an ablation study on the GKIM component of the Mecoin framework. Four variations of GKIM are tested: (1) GKIM with all features enabled, (2) GKIM where node features do not interact with class prototypes, (3) GKIM without local graph structure information, and (4) GKIM without the MeCs module. The results are shown for three datasets: CoraFull, Computers, and CS. Each plot displays the results for a specific dataset and GKIM configuration, illustrating the model’s performance and highlighting the contribution of each component of GKIM.
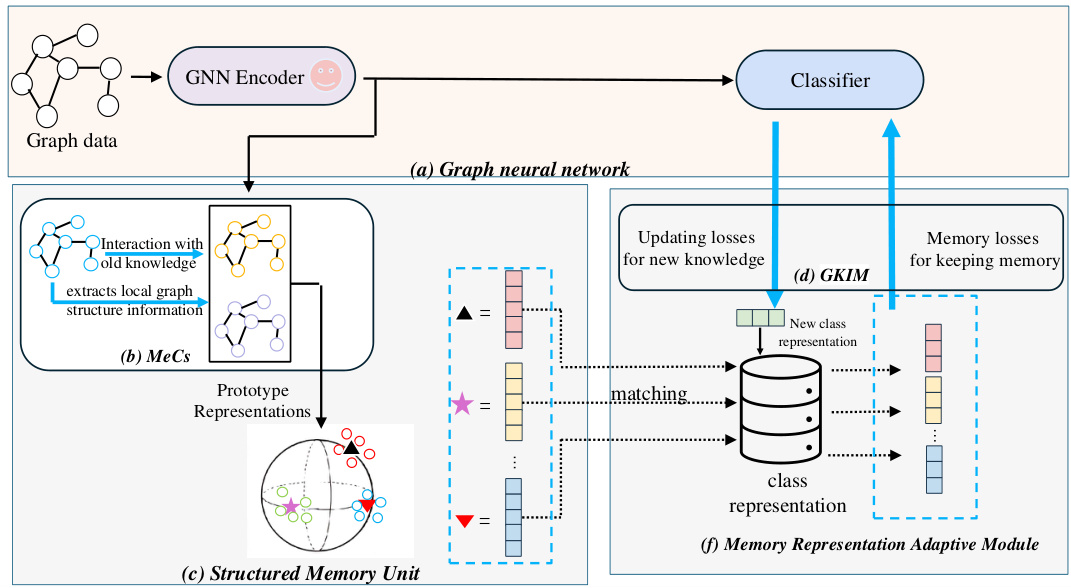
This figure provides a high-level overview of the Mecoin framework, illustrating its key components for graph few-shot class-incremental learning (GFSCIL). It shows how a pre-trained graph neural network (GNN) encoder interacts with the Mecoin’s modules. The Structured Memory Unit (SMU) constructs and stores class prototypes using a Memory Construction Module (MeCs), and the Memory Representation Adaptive Module (MRaM) dynamically manages knowledge interaction with the GNN to avoid catastrophic forgetting.
More on tables
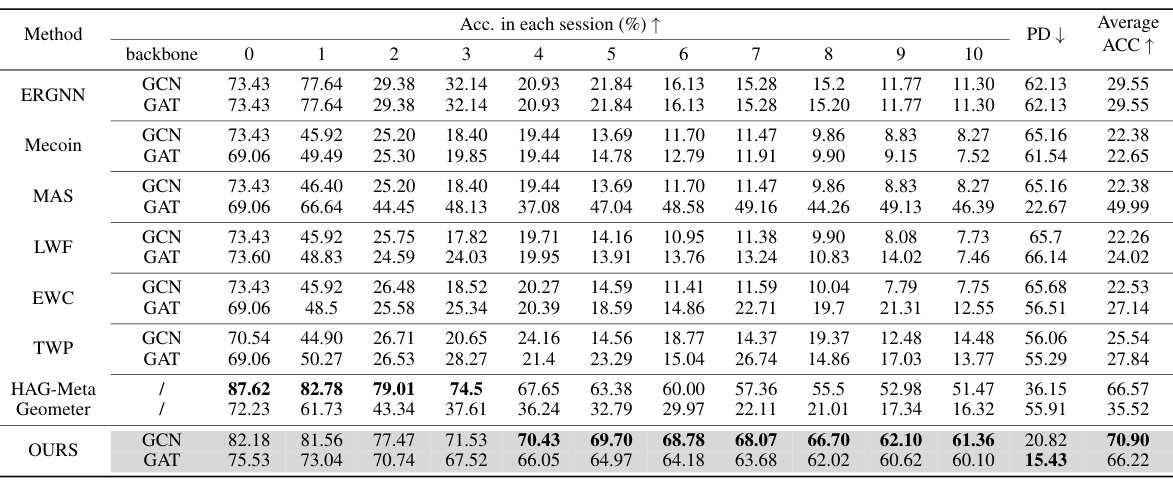
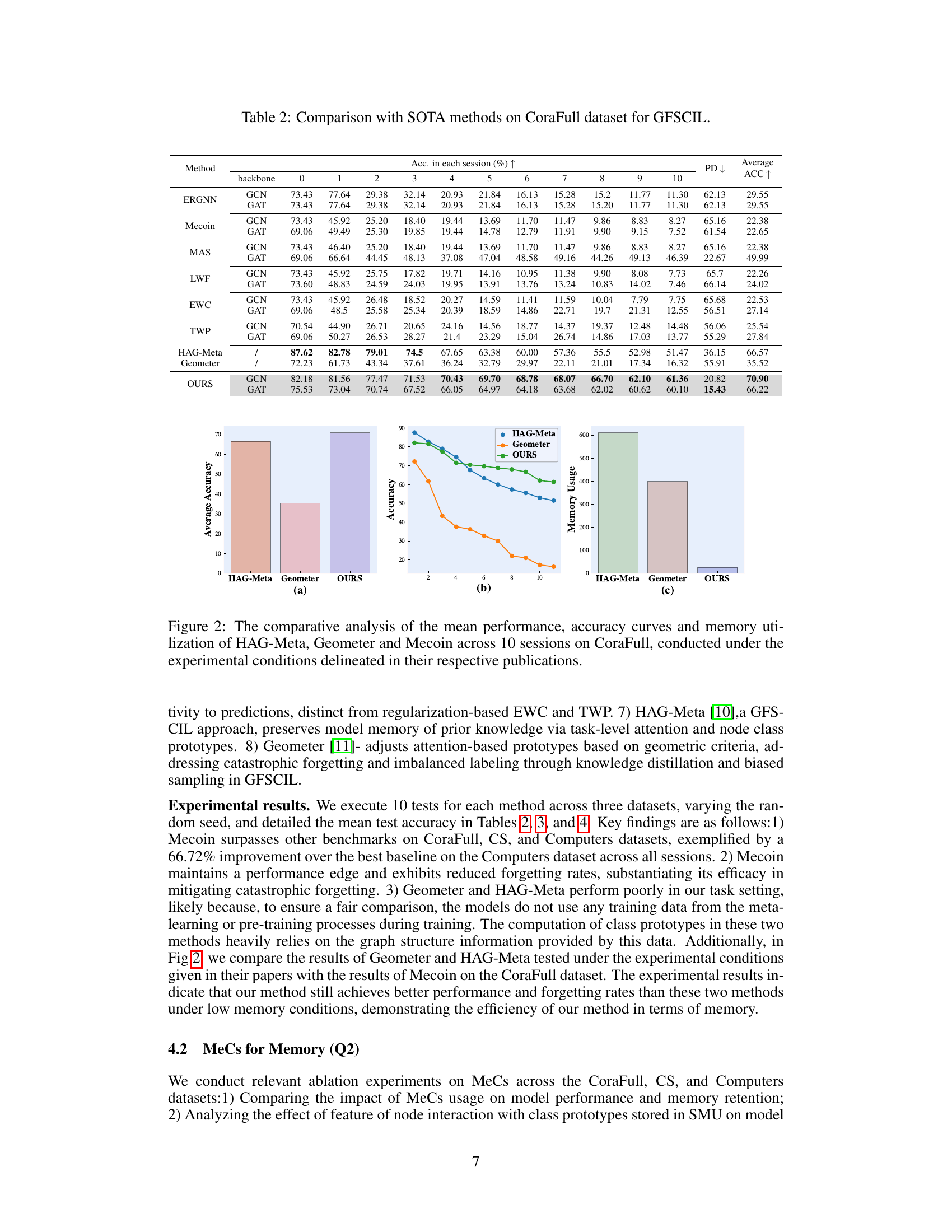
This table compares the performance of Mecoin against other state-of-the-art (SOTA) methods on the CoraFull dataset for the task of graph few-shot class-incremental learning (GFSCIL). It shows the accuracy achieved by each method in each of the ten sessions, along with the average accuracy and forgetting rate (PD). The backbone GNN architecture (GCN or GAT) used by each method is also specified.
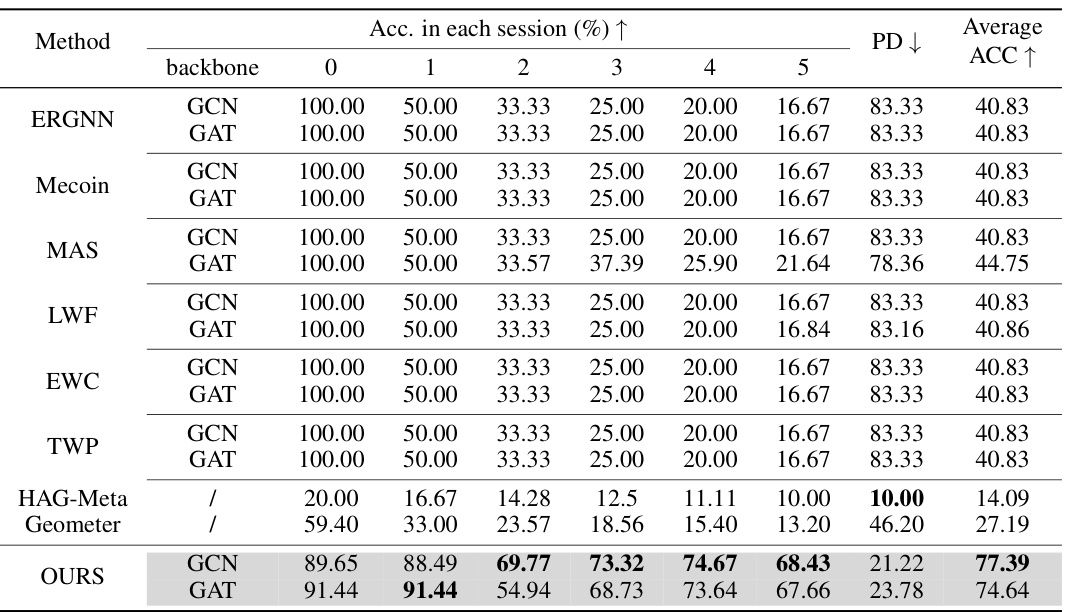
This table compares the performance of Mecoin with other state-of-the-art (SOTA) methods on the Computers dataset for Graph Few-Shot Class-Incremental Learning (GFSCIL). It shows the accuracy achieved by each method in each of the five sessions (0-5), the percentage of data points that were misclassified (PD), and the average accuracy across all sessions. The goal is to evaluate the effectiveness of Mecoin in maintaining prior knowledge while learning new classes from limited samples. The results indicate Mecoin’s superior performance compared to the baselines.
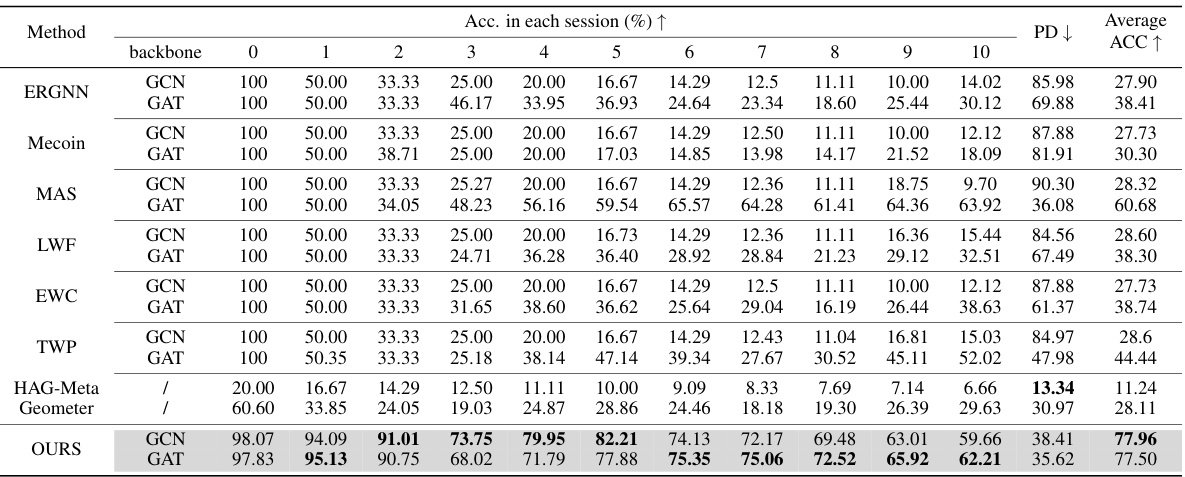
This table compares the performance of Mecoin against other state-of-the-art (SOTA) methods for Graph Few-Shot Class-Incremental Learning (GFSCIL) on the CoraFull dataset. It shows the accuracy achieved by each method in each of ten sessions, the average accuracy across all sessions, and the percentage of data points that are incorrectly predicted (PD). The backbone used for each model (GCN or GAT) is also indicated.
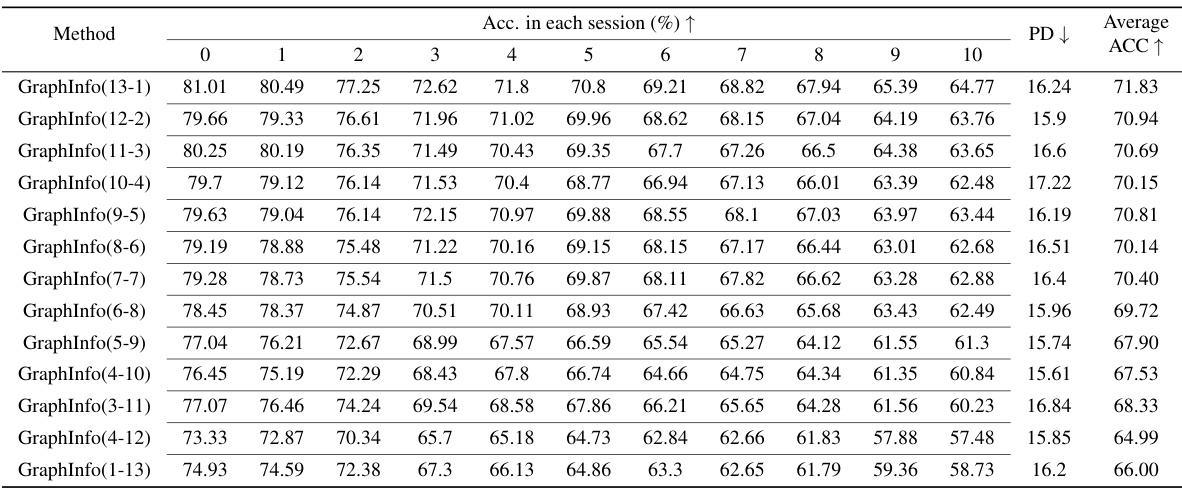
This table compares the performance of Mecoin against other state-of-the-art (SOTA) methods on the CoraFull dataset for graph few-shot class-incremental learning (GFSCIL). It shows the accuracy achieved by each method in each of the ten sessions, along with the average accuracy and forgetting rate (PD). The table allows for a direct comparison of Mecoin’s performance against existing techniques in terms of both accuracy and the ability to retain knowledge learned in previous sessions.
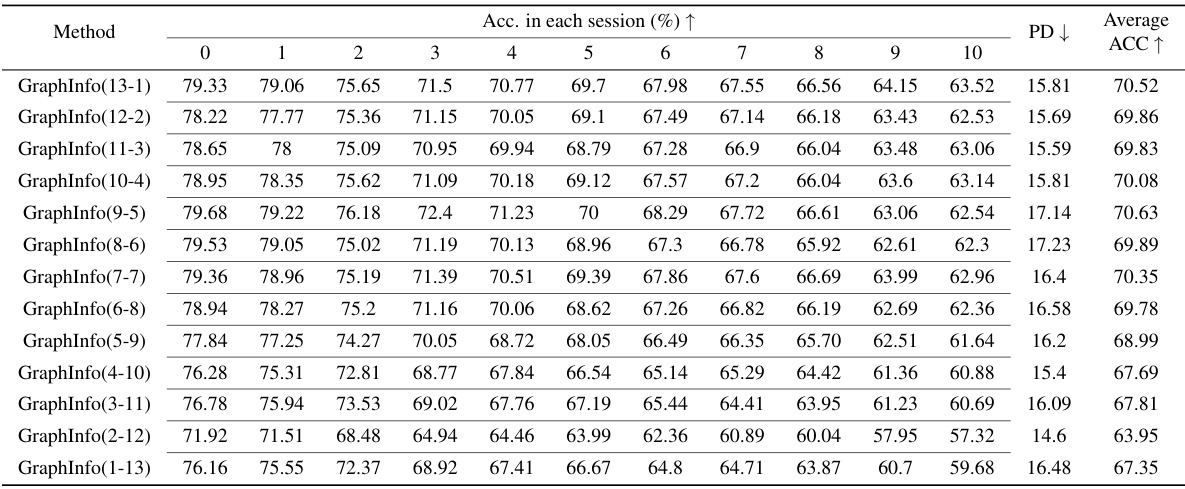
This table presents a comparison of the proposed Mecoin model’s performance against other state-of-the-art (SOTA) methods on the CoraFull dataset for the task of Graph Few-Shot Class-Incremental Learning (GFSCIL). It shows the accuracy achieved by each method in each of the ten sessions, along with the average accuracy and forgetting rate (PD). The table allows for a direct performance comparison between Mecoin and various baseline techniques, demonstrating its effectiveness in handling the GFSCIL task on this specific dataset.

This table compares the performance of the proposed Mecoin method against several state-of-the-art (SOTA) methods on the CoraFull dataset for the Graph Few-Shot Class-Incremental Learning (GFSCIL) task. The table shows the accuracy achieved by each method in each of the ten sessions (0-9) of incremental learning. It also indicates the average accuracy and the Percentage of Data forgotten (PD) for each method. The backbone network used (GCN or GAT) is also specified for each method.
Full paper#