↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many real-world problems exhibit only approximate symmetries, posing challenges for equivariant deep learning models which assume exact symmetries. Current methods for handling approximate symmetries are often limited in applicability. Neural Processes (NPs), being a popular meta-learning model, are greatly impacted by this issue as many real-world datasets which NPs are often used for only have approximate symmetries.
This paper tackles this challenge by developing a general framework for building approximately equivariant architectures. The key idea is to approximate non-equivariant mappings using equivariant ones with additional fixed inputs, effectively relaxing strict equivariance constraints in a data-driven manner. This method is shown to significantly improve the performance of NPs on synthetic and real-world regression tasks, outperforming both strictly equivariant and non-equivariant counterparts.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with equivariant models and meta-learning. It introduces a novel approach to build approximately equivariant neural processes, which are more flexible and robust for real-world applications. The proposed method significantly improves generalisation capabilities and offers a more practical way to leverage symmetries in data, opening exciting new avenues of research for both theoretical and applied research.
Visual Insights#
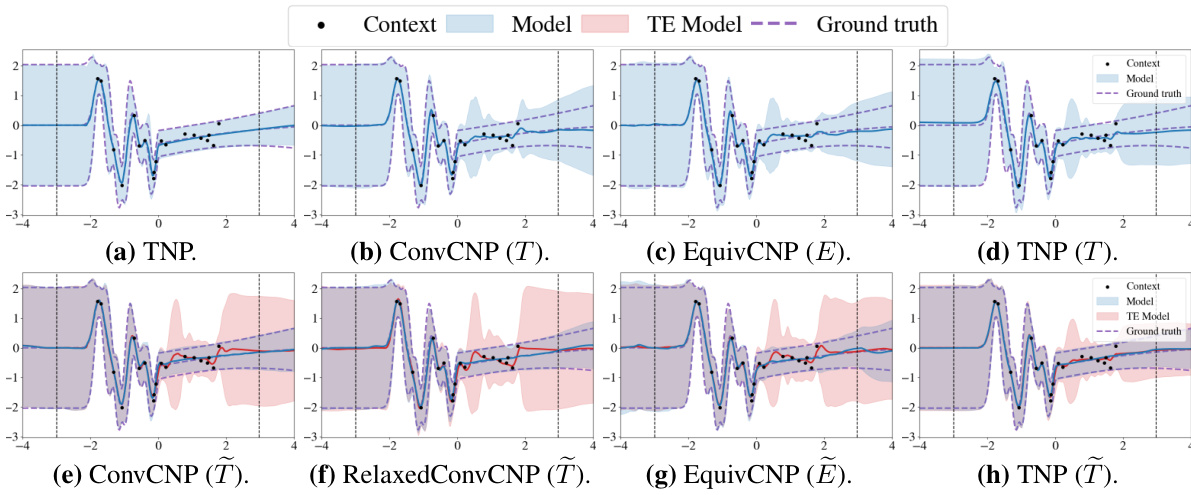
This figure compares the predictive distributions of different neural process models on a single synthetic 1D regression dataset. It highlights the performance of standard (non-equivariant), strictly equivariant, and approximately equivariant models. The approximately equivariant models are shown with and without their additional fixed inputs, illustrating how those inputs affect the predictive distribution and allow for flexibility beyond strict equivariance. The shaded area represents the uncertainty.
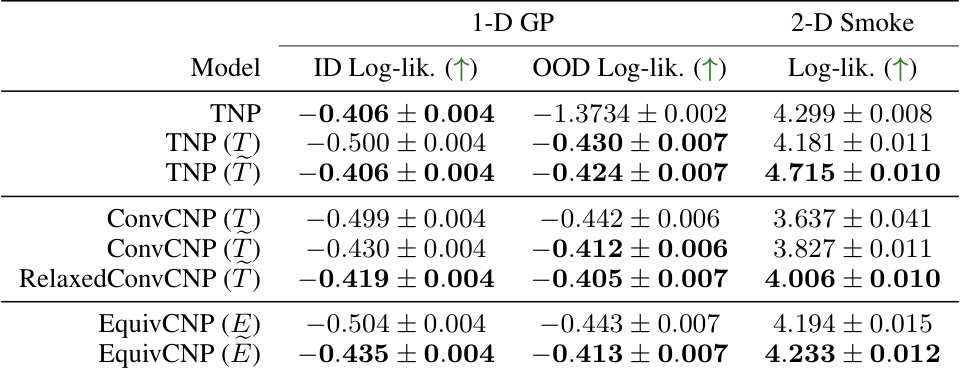
This table presents the average test log-likelihoods achieved by various neural process models on two different experiments: a synthetic 1-D Gaussian process regression task and a 2-D smoke plume simulation. The table is organized by model type (TNP, ConvCNP, RelaxedConvCNP, EquivCNP), showing performance for both in-distribution and out-of-distribution settings (where applicable). The best performing model within each model class is highlighted in bold. Note that different Neural Process variants were used for the 1D and 2D experiments.
In-depth insights#
Approx. Equiv. NPs#
The concept of “Approx. Equiv. NPs” introduces a flexible approach to neural process (NP) design. Traditional equivariant NPs leverage symmetries in data to improve efficiency and generalization, but real-world data often only exhibits approximate symmetries. This section explores how to build NPs that can flexibly adapt to varying degrees of equivariance, departing from strict equivariance when necessary. The approach presented likely involves modifying existing equivariant NP architectures to incorporate additional learnable parameters that control the departure from strict equivariance, enabling data-driven adjustments. A key advantage is the proposed architecture- and symmetry-agnostic nature, making it applicable to various NP types. This method might improve performance over both strictly equivariant and non-equivariant models by achieving a balance between exploiting existing symmetries and adapting to data irregularities. The results would likely demonstrate this improvement across multiple regression tasks involving both synthetic and real-world data, suggesting that approximation flexibility is key to improving performance in scenarios with complex real-world data.
Equiv. Decomp. Thm#
The core idea behind an ‘Equivariant Decomposition Theorem’ revolves around approximating non-equivariant functions using equivariant ones. This is crucial because real-world data often only exhibits approximate, not exact, symmetries. The theorem likely establishes conditions under which a non-equivariant mapping between function spaces can be approximated arbitrarily well by an equivariant mapping with additional fixed inputs. This decomposition is significant because it allows us to leverage the efficiency and generalizability benefits of equivariant architectures while accommodating the imperfections of real-world data. The proof probably involves techniques from functional analysis, such as the approximation of compact operators or the use of a specific basis to separate equivariant and non-equivariant components. The additional inputs act as a correction factor, compensating for the discrepancy between the exact symmetry and its approximate realization in the data. The theorem’s strength lies in its generality—it might be applicable to various symmetry groups and model architectures, which greatly expands its practical utility in machine learning. A key aspect is the trade-off between approximation accuracy and the number of additional inputs; more inputs generally allow for better approximations, but this may come at the cost of increased model complexity.
Empirical Eval.#
An empirical evaluation section in a research paper should thoroughly investigate the claims made. It needs to present results from multiple experiments across various datasets, clearly demonstrating the effectiveness of the proposed methods compared to relevant baselines. The presentation should go beyond simply reporting numbers; it must involve a detailed analysis of those numbers, including discussion of the statistical significance of the findings and error bars. The evaluation should highlight both the strengths and weaknesses of the approach, including potential failure cases and their causes. The section’s strength lies in its ability to showcase the practical impact and generalizability of the research, answering the question of how well the proposed method works in the real world, or within different scenarios.
Generalization#
The concept of generalization is central to the success of machine learning models, and this paper explores it within the context of approximately equivariant neural processes (NPs). True equivariance, while beneficial, is often unrealistic for real-world data, which frequently exhibit only approximate symmetries. The authors show that approximately equivariant models offer a way to leverage the advantages of equivariance without the limitations of strict adherence. Their approach shows improved performance on synthetic and real-world tasks compared to both strictly equivariant and non-equivariant counterparts, suggesting that this flexible approach to symmetry can greatly improve generalization. The core innovation is a methodology for constructing approximately equivariant models from existing equivariant architectures, agnostic to the specific symmetry group and model choice. Theoretical results provide a sound basis for this approach, underpinning the flexibility and broad applicability of the method. However, future work should focus on more precisely quantifying and controlling the degree of equivariance relaxed, as this would aid in better understanding and utilizing this valuable property for real-world applications.
Future Work#
Future research directions stemming from this work on approximately equivariant neural processes are plentiful. Rigorously quantifying and controlling the degree to which these models depart from strict equivariance is crucial. Current methods offer a probabilistic approach, but a more precise, deterministic measure is needed. Further exploration into more sophisticated methods for incorporating approximate equivariance into various architectures beyond the simple additions used here is warranted. Scaling these models to larger, more complex datasets and real-world problems is also a significant challenge. The current experiments, while demonstrating efficacy, are relatively small-scale. The generalizability to more complex scenarios, such as those with high-dimensional inputs and varying degrees of symmetry-breaking, needs further investigation. Finally, a deeper theoretical analysis exploring the relationship between the number of added inputs and approximation error would provide valuable insights into model design and optimization strategies. Understanding the interplay between approximate equivariance and generalization performance is a key area requiring more in-depth exploration. This would involve testing on diverse datasets, assessing robustness to various noise levels, and exploring the implications of different model architectures and training methodologies.
More visual insights#
More on figures
This figure compares the predictive distributions of three different types of neural process models (TNP, ConvCNP, and EquivCNP) on a single synthetic 1D regression dataset. It highlights how the approximately equivariant models (those incorporating the approach described in the paper) balance strict equivariance with the ability to model non-equivariant aspects of the data. The plot shows both the standard model prediction and a prediction without utilizing the fixed inputs (representing the strictly equivariant case).

This figure compares the predictive distributions of three different types of neural process models (TNP, ConvCNP, and EquivCNP) on a single synthetic 1D regression dataset. It highlights the impact of incorporating approximate equivariance. The blue lines represent the predictive distribution of the approximately equivariant model, while the red lines show the distribution obtained when the additional fixed inputs that break strict equivariance are removed. The dotted black lines show the range of target values.

This figure compares the predictive distributions of three different types of neural process models (TNP, ConvCNP, and EquivCNP) on a single 1D synthetic regression dataset. The key takeaway is the performance of approximately equivariant models; they balance the benefits of equivariance (generalization) with the flexibility to account for deviations from strict symmetry in real-world data, achieving better performance than both strictly equivariant and non-equivariant models.

This figure compares the predictive distributions of various neural process models on a single synthetic 1-D regression dataset. It highlights the differences between non-equivariant, strictly equivariant, and approximately equivariant models. The approximately equivariant models are shown with and without the additional fixed inputs that break strict equivariance. The comparison allows visualization of how these modifications affect model predictions and uncertainty estimation.
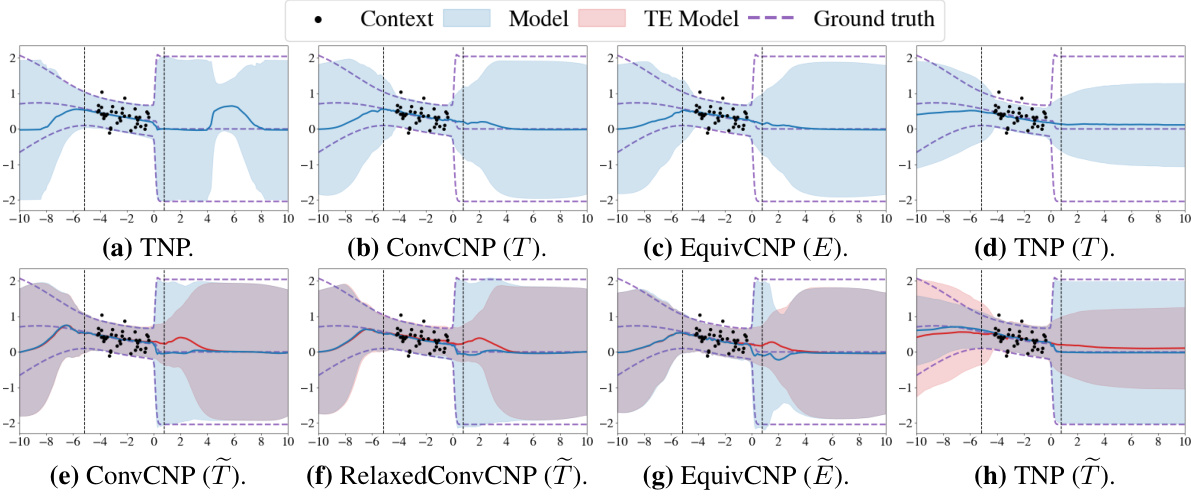
This figure compares the predictive distributions of various neural process (NP) models on a single synthetic 1D regression dataset. The models shown include standard non-equivariant NPs, strictly equivariant NPs, and approximately equivariant NPs (the latter created using the method presented in the paper). The figure highlights how the approximately equivariant models balance between the flexibility of non-equivariant models and the efficiency of equivariant models. The use of red lines to illustrate the results without fixed inputs emphasizes the impact of the method developed for achieving approximate equivariance.
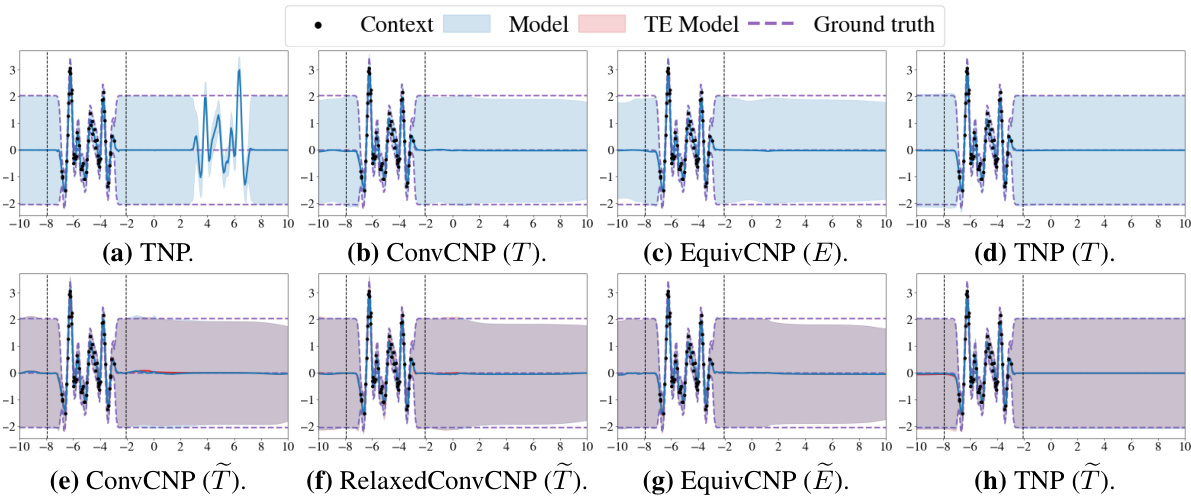
This figure compares the predictive distributions of several neural process models (TNP, ConvCNP, EquivCNP) on a single synthetic 1D regression dataset. It highlights the performance of approximately equivariant models by contrasting their predictive distributions with those of their strictly equivariant and non-equivariant counterparts. The use of fixed inputs in the approximately equivariant models is shown by comparing their full predictive distribution with the distribution obtained when these fixed inputs are zeroed out. The target range is also indicated.
This figure compares the predictive distributions of three different types of neural process models (TNP, ConvCNP, and EquivCNP) on a single synthetic 1D regression dataset. It highlights how the approximately equivariant models (shown in blue) balance flexibility (departing from strict equivariance) with generalizability (closely matching the predictions of their strictly equivariant counterparts). The red lines in the approximately equivariant model plots show what the predictions would have been if the non-equivariant components of the models were not used.

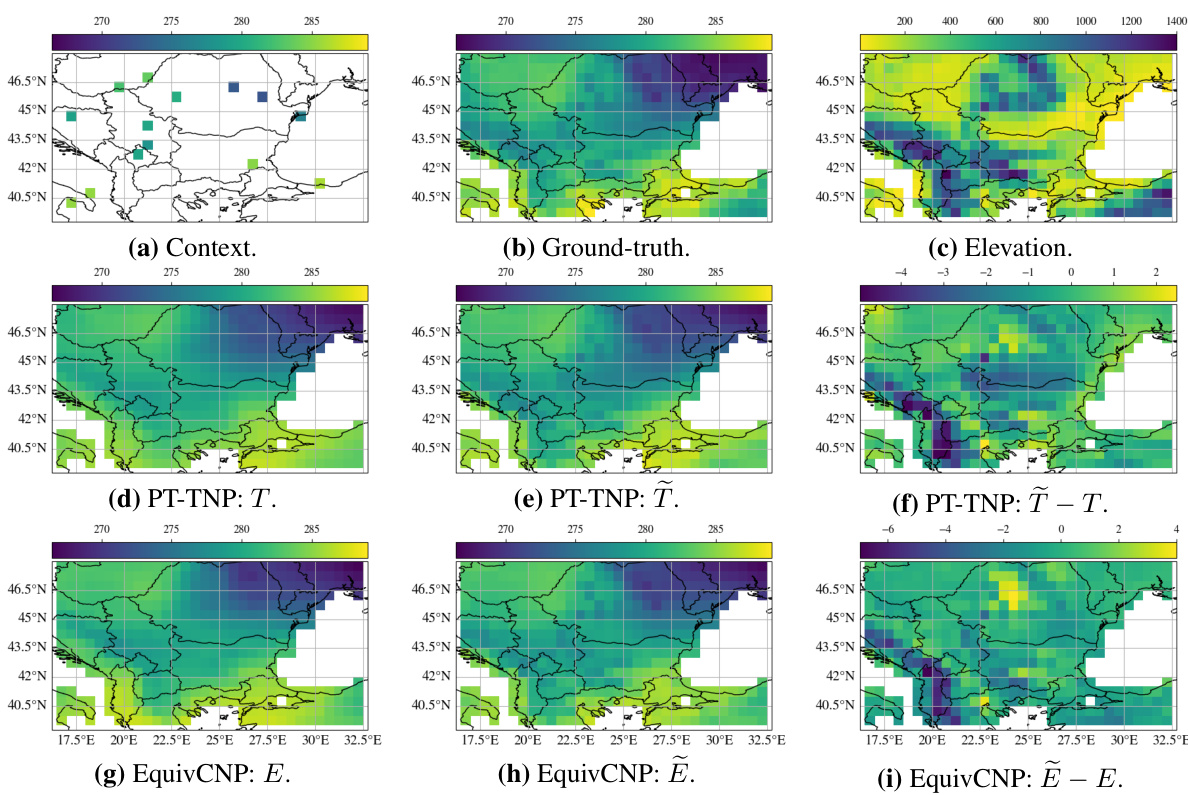
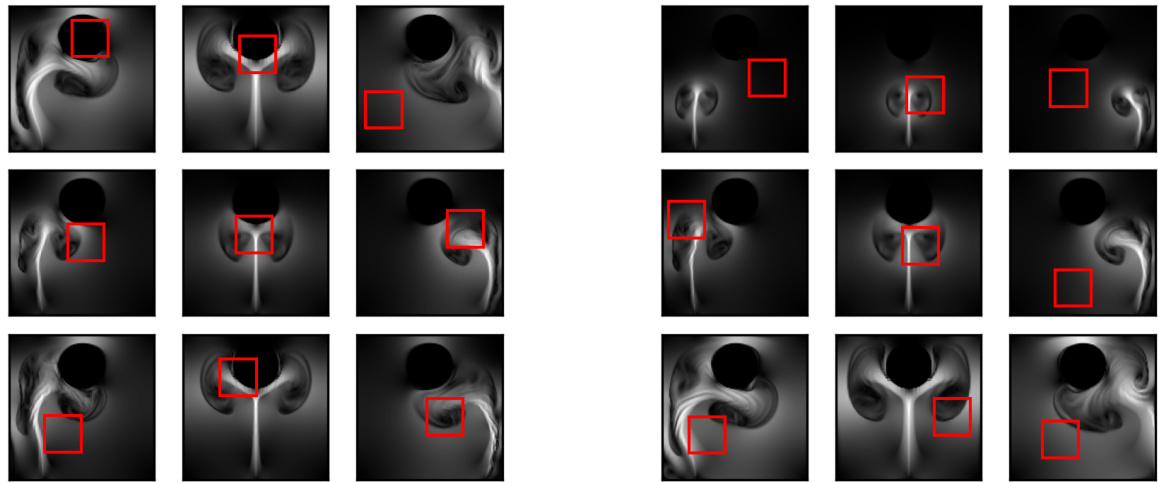
This figure compares the predictive means of different models on a smoke plume dataset. The top row displays the predicted means for several models: ground truth, non-equivariant, equivariant, and approximately equivariant versions of PT-TNP, ConvCNP, and EquivCNP. The bottom row shows the absolute differences between each model’s prediction and the ground truth. This allows for a visual comparison of how well each model’s predictions match the ground truth, and how approximate equivariance affects performance.
More on tables
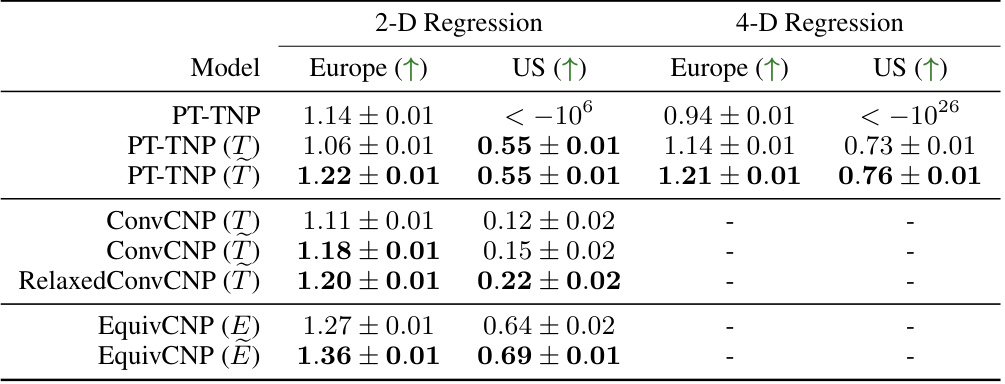
This table presents the results of the 2D and 4D environmental regression experiments. It compares the average test log-likelihoods achieved by various neural process models (non-equivariant, equivariant, and approximately equivariant) on two different geographical regions (Europe and the US). The models are grouped by their underlying architecture, and the best performing model within each group is highlighted in bold. The table allows for comparison of model performance across different levels of equivariance (strict, approximate, and none) and dimensionality of the input data (2D vs 4D).
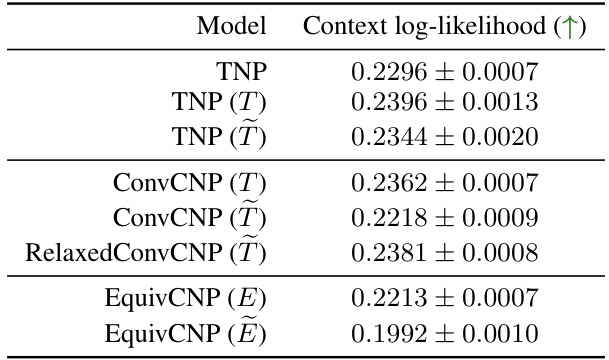
This table presents the average test log-likelihoods achieved by different neural process models on the synthetic 1-D Gaussian Process dataset when only tested on the context sets (i.e., without the target sets). The models include the non-equivariant TNP, equivariant versions of the TNP, ConvCNP, and EquivCNP, and approximately equivariant counterparts of the TNP and ConvCNP models. The ground truth log-likelihood is provided for comparison. This allows to measure the model’s ability to accurately reconstruct the context set, which is a key component of the neural process.
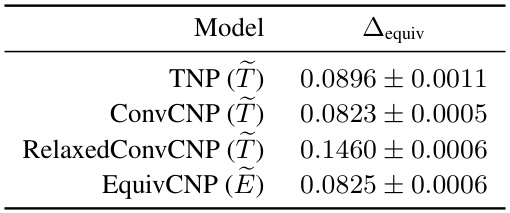
This table presents the equivariance deviation (Δequiv) for each of the approximately equivariant models evaluated in the 1D synthetic GP experiment. The equivariance deviation is calculated as the L1 norm of the difference between the predictive mean of the approximately equivariant model and the predictive mean of the strictly equivariant model (obtained by zeroing out the fixed inputs). This metric quantifies how much the approximately equivariant model deviates from strict equivariance. Lower values indicate a closer adherence to strict equivariance.

This table presents the average test log-likelihoods achieved by two different models, TNP (T) and ConvCNP (T), under various numbers of fixed inputs (0, 1, 2, 4, 8, 16). It shows how the model performance changes as the number of fixed inputs increases, illustrating the impact of adjusting the degree of approximation to equivariance. All standard deviations across the different numbers of fixed inputs are consistently 0.004.
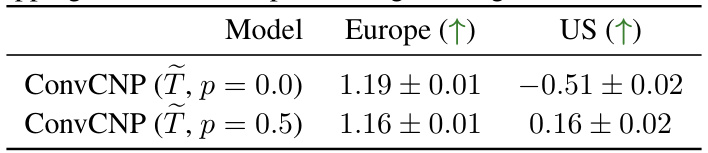
This table presents the average test log-likelihoods achieved by two different ConvCNP models in a 2D environmental regression experiment. The models differ in the probability (p) of dropping out the fixed inputs during training. The results show the log-likelihoods for both Europe and the US regions. The values show that using a dropout probability of 0.5 improves out-of-distribution generalization to the US.
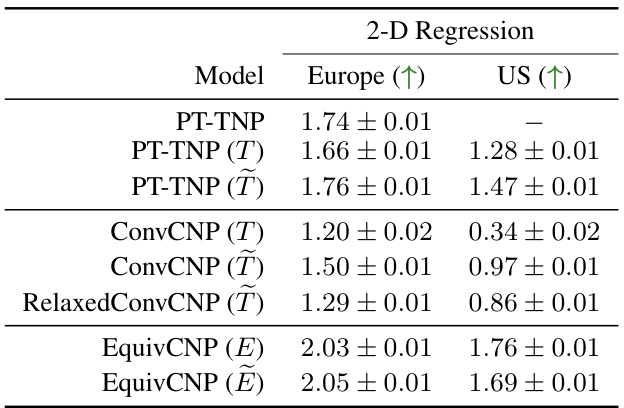
This table presents the results of the 2D and 4D environmental regression experiments. It compares the average test log-likelihoods achieved by different neural process models (PT-TNP, ConvCNP, RelaxedConvCNP, EquivCNP) under different conditions of equivariance: strictly equivariant, approximately equivariant, and non-equivariant. The best performing model within each class is highlighted in bold. The data used is ERA5 surface air temperature data for Europe and the central US.
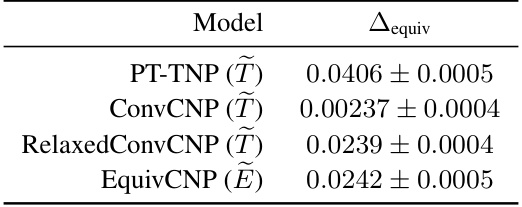
This table presents the equivariance deviation (Δequiv) for each of the approximately equivariant models used in the 2-D environmental regression experiment. The equivariance deviation is a measure of how much the approximately equivariant model deviates from a strictly equivariant model. A lower value indicates a closer approximation to strict equivariance. The table shows that the approximately equivariant models generally have low equivariance deviation, indicating that they are only slightly deviating from strict equivariance.

This table shows the average test log-likelihoods for the ConvCNP (T) model in the 2-D environmental regression experiment. The results are broken down by the number of additional fixed inputs used in the model (0, 1, 2, 4, 8, and 16), with the likelihoods calculated for the Europe region. The table demonstrates how the model performance changes as the number of fixed inputs increases.
Full paper#