↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Local differential privacy (LDP) protects individual data, but its inherent perturbation reduces data utility. This paper focuses on the “private sampling” problem, where each client holds a dataset and aims to privately release a sample from its dataset. Existing solutions often rely on arbitrary choices that affect their performance. The lack of a fundamental understanding of this privacy-utility trade-off limits the development of truly efficient and accurate private sampling methods.
This research addresses these limitations. The authors rigorously define the optimal privacy-utility trade-off for private sampling and propose new sampling mechanisms that are proven to be universally optimal across a wide range of utility measures. The mechanisms’ superiority over baselines is demonstrated numerically for both finite and continuous data spaces. This research establishes a solid theoretical foundation for private sampling and provides universally optimal mechanisms, significantly advancing the state-of-the-art in privacy-preserving data analysis.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in differential privacy and machine learning. It provides rigorous theoretical foundations for private sampling, a fundamental task with wide applications in generative models and other privacy-preserving techniques. The work offers universally optimal mechanisms, resolving a critical open problem and providing a benchmark for future research. It also opens avenues for exploring more efficient algorithms and evaluating their performance in various applications.
Visual Insights#

This figure compares the original data distribution (a Gaussian ring distribution) with the sampling distributions produced by the baseline method from a previous work ([35]) and the proposed method. The privacy budget (epsilon) is set to 0.5. The image visually demonstrates that the proposed mechanism produces a sampling distribution that is much closer to the original distribution than the baseline method.
In-depth insights#
Minimax PUT Defined#
A section titled ‘Minimax PUT Defined’ in a PDF research paper would likely formalize the privacy-utility trade-off (PUT) using a minimax framework. This approach would be crucial for establishing rigorous guarantees about the performance of a privacy-preserving mechanism, particularly in adversarial settings where an attacker might exploit weaknesses in the utility measure. The minimax formulation would involve defining a worst-case utility, minimizing the maximum possible divergence between the original and the privatized data. It would likely consider different f-divergences as utility measures, reflecting various notions of distance between distributions. The section would likely discuss optimal mechanisms and their minimax utilities, providing theoretical bounds on the achievable privacy-utility balance. Proofs and detailed mathematical analyses would underpin these claims, and a precise, formal definition of the minimax PUT would be essential. This formalization would be a key contribution, providing a foundation for further research and practical applications in privacy-preserving machine learning.
Optimal Samplers#
The concept of ‘Optimal Samplers’ in the context of locally differentially private (LDP) mechanisms is crucial for balancing privacy and utility. Optimality is typically defined in a minimax sense, aiming to minimize the worst-case divergence between the original data distribution and the one produced by the sampler. This minimax framework is important because it provides strong guarantees, regardless of the specific data distribution encountered. The paper likely explores several samplers and rigorously proves the optimality of a specific mechanism, potentially through a theoretical analysis. This theoretical analysis is important for establishing the fundamental limits of privacy-preserving sampling. The study may further include numerical experiments to showcase the practical performance of the optimal samplers compared to alternative approaches, highlighting their advantage in specific settings or data types. The development of such universally optimal samplers for all f-divergences is a significant theoretical contribution, demonstrating strong privacy and utility guarantees under a wide range of divergence measures. This is important, as the choice of divergence impacts the evaluation and interpretation of the sampler’s performance. Ultimately, the study of ‘Optimal Samplers’ in LDP significantly advances the field by providing both theoretically sound and practically efficient solutions for privacy-preserving data analysis.
Finite Space PUT#
The concept of ‘Finite Space PUT’ (Privacy-Utility Trade-off) in the context of local differential privacy (LDP) focuses on scenarios with a finite data domain. This simplification allows for a precise characterization of the optimal privacy-utility balance. The key advantage is the derivation of closed-form expressions for the minimax utility, avoiding the complexities of continuous spaces. This closed-form solution enables a complete theoretical understanding of the fundamental limits and optimal mechanisms for private sampling. Universally optimal mechanisms are identified, achieving the minimax optimal PUT regardless of the specific f-divergence used as the utility metric. Numerical experiments demonstrate the superiority of the proposed mechanisms over existing baselines in finite data spaces, confirming the theoretical findings. However, it’s crucial to note the limitations of the finite space assumption; it may not accurately represent many real-world data distributions, which are often continuous and high-dimensional. The finite-space assumption represents a critical theoretical stepping stone for understanding more complex scenarios.
Continuous PUT#
The concept of “Continuous PUT” (Privacy-Utility Trade-off) in a research paper would likely explore the scenario where data is not discrete but continuous. This requires a shift from analyzing individual data points (as in a discrete setting) to working with probability distributions representing the underlying data generating process. The analysis would need to address how different privacy mechanisms affect the continuous probability distribution, considering the trade-off between privacy guarantees (e.g., using a specific divergence measure) and the preservation of relevant information. A key challenge is defining appropriate metrics for utility in the continuous domain that capture the essence of the data’s characteristics. The minimax framework would likely be employed to determine the optimal mechanism under worst-case conditions. A continuous PUT analysis will likely include theoretical results characterizing the optimal trade-off, which could be extended to cover specific families of probability distributions. Finally, experimental validation using simulated or real continuous data would help demonstrate the theoretical bounds and potentially suggest more practical mechanisms that perform well in scenarios where the probability distributions are not perfectly known.
Future Work#
The “Future Work” section of a differential privacy research paper could explore several promising directions. Extending the theoretical framework to handle more complex data structures and distributions beyond the finite and continuous spaces analyzed in the paper would enhance its applicability. This could involve investigating scenarios with high-dimensional data or those incorporating temporal dependencies. Developing practical algorithms that effectively approximate optimal solutions while maintaining computational efficiency is also crucial. The current numerical experiments demonstrate the superiority of the proposed mechanism, but scalability remains a challenge. Furthermore, research into robust mechanisms that are less sensitive to noise and outliers could significantly enhance their usefulness in real-world applications, where data quality is often imperfect. Finally, investigating the privacy-utility trade-off under various forms of attacks is necessary to fully understand the efficacy of the proposed private sampling mechanisms. This requires a deeper analysis of the vulnerabilities and how these mechanisms could be strengthened against adversarial attacks. Further exploration of the relationship between the minimax utility and more nuanced performance metrics is vital to provide a comprehensive view of the method’s practicality.
More visual insights#
More on figures

This figure compares the original Gaussian ring distribution with the sampling distributions generated by the baseline method from a previous study [35] and the proposed mechanism in this paper. The privacy budget (∈) is set to 0.5. The figure visually demonstrates how well the proposed mechanism preserves the original distribution’s shape compared to the baseline, which shows noticeable differences. The details of the implementation can be found in Appendix F of the paper.
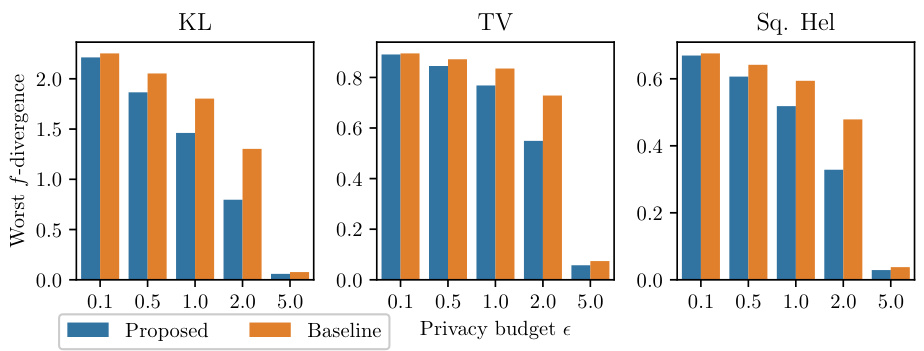
This figure compares the theoretical worst-case f-divergences of the proposed optimal private sampling mechanism and the previously proposed baseline mechanism for three common f-divergences (KL divergence, Total Variation distance, Squared Hellinger distance) across different privacy budgets (epsilon). The x-axis represents the privacy budget (epsilon), and the y-axis represents the worst-case f-divergence. The results demonstrate the superior performance of the proposed mechanism, achieving significantly lower worst-case f-divergences across all tested f-divergences and privacy budgets.
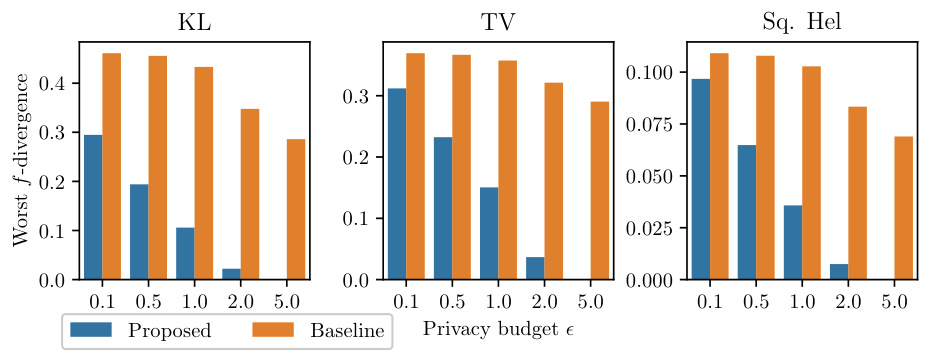
This figure compares the theoretical worst-case f-divergences of the proposed mechanism and the baseline method from [35] for a finite data space with k=10 and varying privacy budgets (epsilon). Three different f-divergences are shown: Kullback-Leibler (KL) divergence, Total Variation (TV) distance, and Squared Hellinger distance. The results demonstrate that the proposed mechanism consistently achieves lower worst-case f-divergences across all three metrics and privacy budgets.
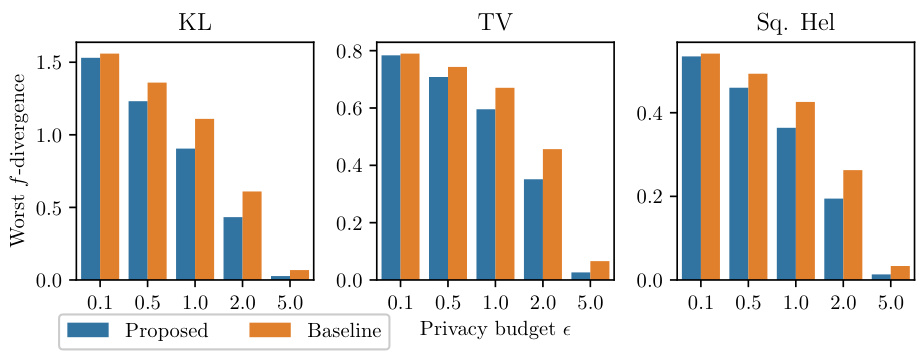
This figure compares the theoretical worst-case f-divergences of the proposed optimal mechanism and the baseline mechanism from Husain et al. [35] for different privacy budgets (epsilon). The comparison is shown for three common f-divergences: Kullback-Leibler (KL) divergence, Total Variation (TV) distance, and Squared Hellinger distance. The results demonstrate that the proposed mechanism consistently achieves lower worst-case f-divergences than the baseline, particularly in the medium privacy regime. The difference is significant for KL divergence and TV distance, but less pronounced for Squared Hellinger distance.
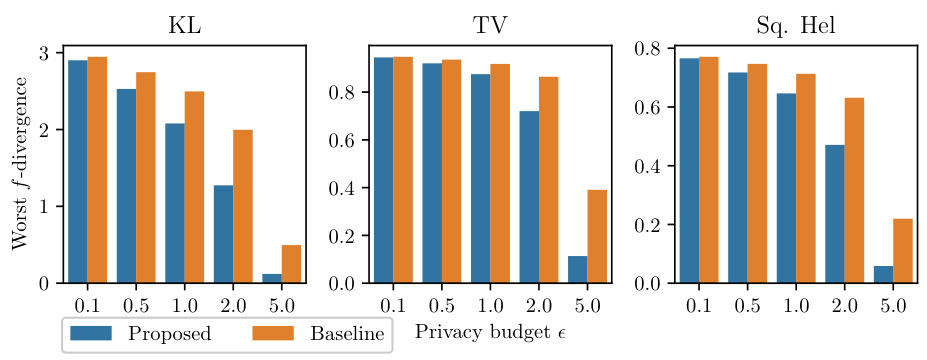
This figure compares the theoretical worst-case f-divergences of the proposed mechanism and the baseline mechanism for different privacy budgets (epsilon). The comparison is done for three different f-divergences: KL divergence, Total Variation distance, and Squared Hellinger distance. The results show that the proposed mechanism consistently achieves a lower worst-case f-divergence than the baseline mechanism across all privacy budgets and f-divergences. The size of the data space is k=10.
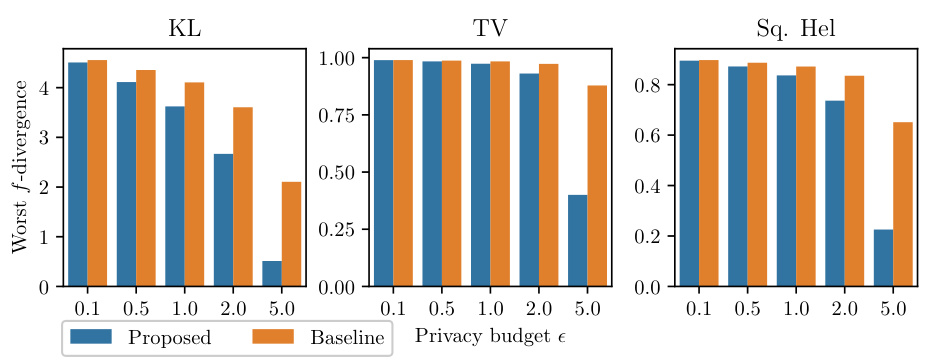
This figure compares the theoretical worst-case f-divergences of the proposed mechanism and the baseline mechanism from [35] for different privacy budgets (epsilon) and three types of f-divergences (KL-divergence, Total Variation distance, and squared Hellinger distance). The results demonstrate the superiority of the proposed mechanism over the baseline, especially in the medium privacy regime.
Full paper#



















