TL;DR#
Time series forecasting is crucial across various domains, but existing diffusion models suffer from instability due to limited datasets and a lack of guidance during the prediction process. This paper introduces a novel solution: the Retrieval-Augmented Time series Diffusion model (RATD). RATD tackles these issues by incorporating a two-part framework: an embedding-based retrieval process that identifies relevant historical data and a reference-guided diffusion model that uses these references to improve prediction accuracy. The retrieval process effectively maximizes the use of available data, while the reference-guided diffusion model overcomes the guidance deficiency.
The proposed RATD method demonstrates significant improvements in forecasting accuracy and stability, particularly in complex scenarios. The model’s effectiveness is demonstrated across multiple datasets, showcasing its ability to handle challenging prediction tasks. This contribution offers a new paradigm in time series forecasting, addressing critical limitations and paving the way for more robust and accurate predictions.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses the instability issue of existing time series diffusion models by proposing a novel Retrieval-Augmented Time series Diffusion model (RATD). RATD tackles data insufficiency and lack of guidance, common limitations in time series forecasting, opening new avenues for research and improving the accuracy and reliability of time series predictions across various domains. The approach of combining retrieval with diffusion models offers a novel paradigm, impacting research in fields like weather forecasting, finance, and healthcare.
Visual Insights#
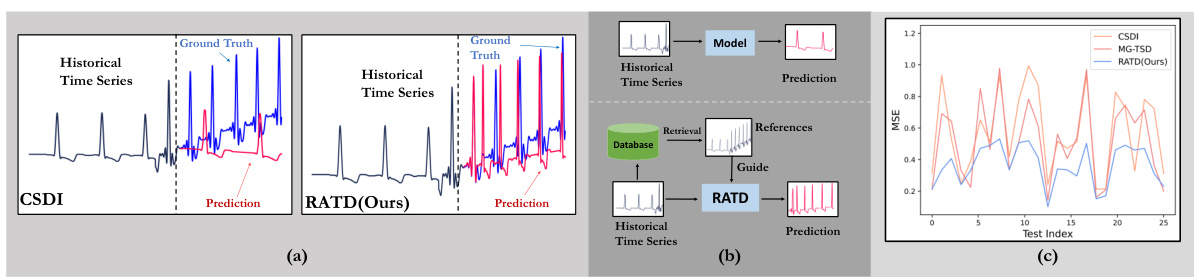
🔼 This figure compares the performance of the proposed RATD model with existing time series diffusion models (CSDI and MG-TSD) on time series forecasting tasks. Subfigure (a) shows that RATD makes much more accurate predictions than CSDI for cases with small proportion in the training set, by retrieving meaningful references. Subfigure (b) illustrates the framework of RATD, which consists of retrieval process and reference-guided diffusion model, comparing it with the conventional framework. Subfigure (c) demonstrates that RATD is more stable in handling complex prediction tasks than CSDI and MG-TSD by showing the mean squared error (MSE) of 25 forecasting tasks on the electricity dataset.
read the caption
Figure 1: (a) The figure shows the differences in forecasting results between the CSDI [36] (left) and RATD (right). Due to the very small proportion of such cases in the training set, CSDI struggles to make accurate predictions, often predicting more common results. Our method, by retrieving meaningful references as guidance, makes much more accurate predictions. (b) A comparison between our method's framework(bottom) and the conventional time series diffusion model framework(top). (c) We randomly selected 25 forecasting tasks from the electricity dataset. Compared to our method, CSDI and MG-TSD [9] exhibited significantly higher instability. This indicates that the RATD is better at handling complex tasks that are challenging for the other two methods.
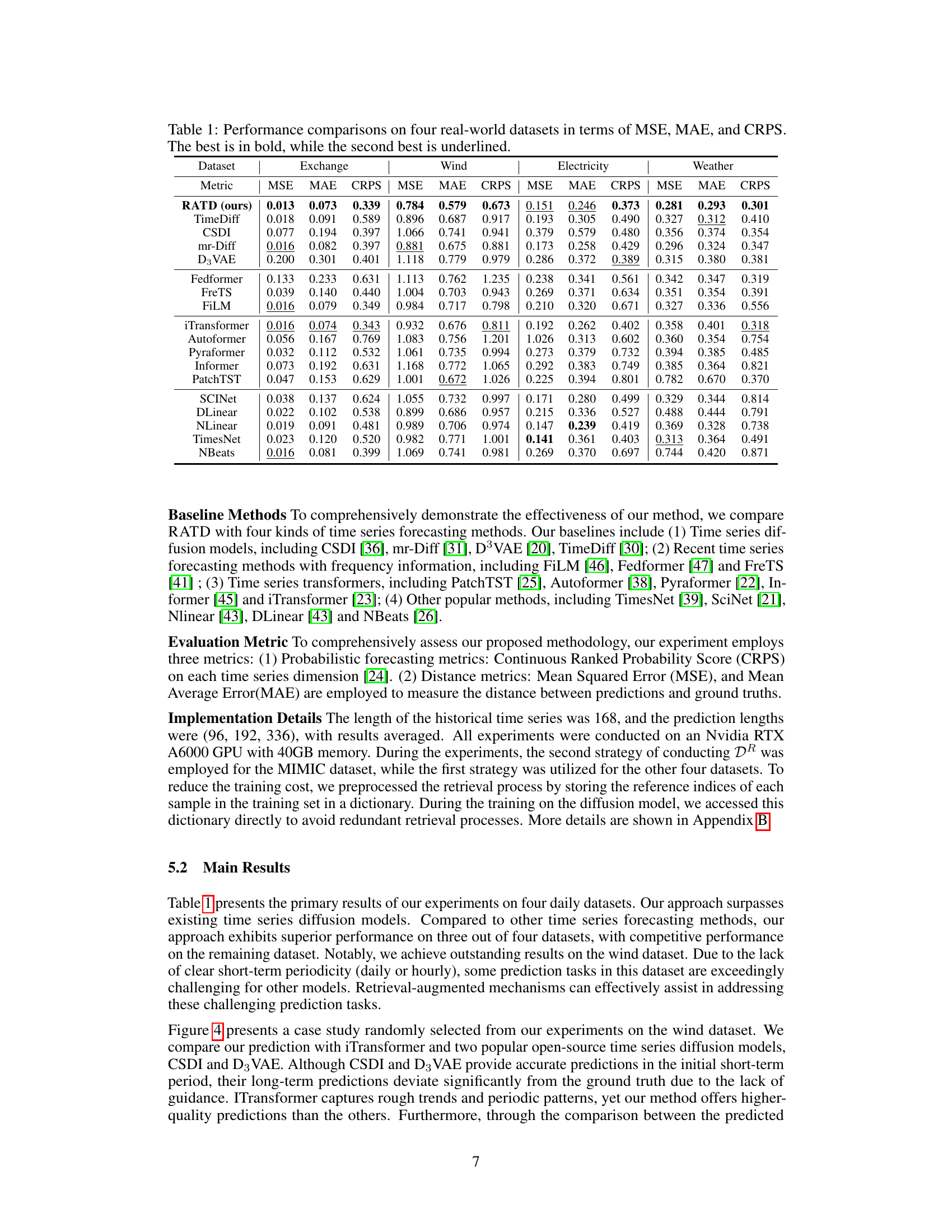
🔼 This table presents a comparison of the proposed RATD model’s performance against various baseline methods on four real-world datasets. The performance is evaluated using three metrics: Mean Squared Error (MSE), Mean Absolute Error (MAE), and Continuous Ranked Probability Score (CRPS). The best performing model for each metric on each dataset is shown in bold, and the second-best is underlined, allowing for easy comparison of the different approaches across various datasets and evaluation metrics.
read the caption
Table 1: Performance comparisons on four real-world datasets in terms of MSE, MAE, and CRPS. The best is in bold, while the second best is underlined.
In-depth insights#
Retrieval-Augmented Diffusion#
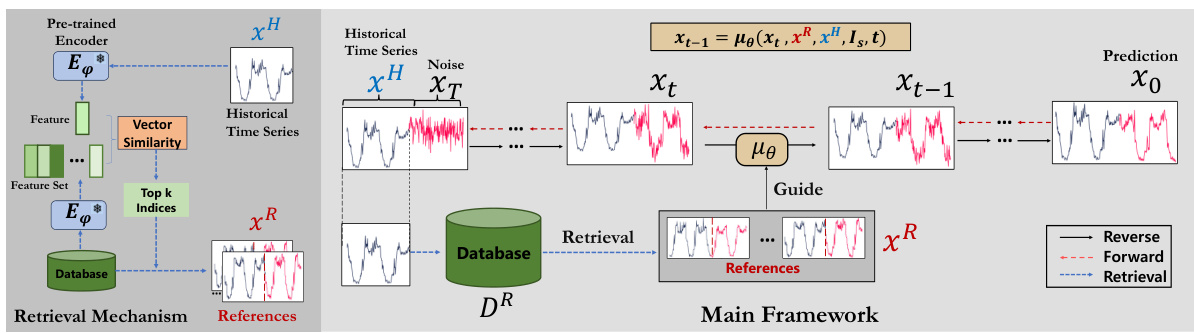
Retrieval-augmented diffusion models represent a powerful paradigm shift in generative modeling, particularly for time series forecasting. By integrating a retrieval mechanism into the diffusion framework, these models address critical limitations of traditional diffusion approaches. The core idea is to leverage a database of relevant past time series to guide the generation process. This provides a form of ‘contextual guidance’ that standard diffusion models often lack, resulting in improved stability and accuracy, especially when handling complex or imbalanced datasets. The retrieval process itself can be sophisticated, employing techniques like embedding-based similarity search, allowing the model to find the most relevant past time series efficiently. The integration of retrieved information can occur at various points in the diffusion process, through mechanisms like attention modules. This enables the model to dynamically incorporate the insights from past instances for better predictions. Overall, the combination of diffusion models’ capability to generate complex time series distributions with the external knowledge provided through retrieval creates a robust and adaptable method. It is particularly powerful in addressing situations where limited training data or data imbalance hinders standard diffusion model performance.
Reference-Guided Denoising#
Reference-guided denoising, in the context of diffusion models for time series forecasting, is a crucial innovation addressing the instability of existing methods. It leverages a retrieval mechanism to identify relevant past time series from a database that serve as references. These references, rather than acting as simple inputs, actively guide the denoising process of the diffusion model. This guidance is particularly beneficial for handling complex and imbalanced datasets, a common challenge in time series forecasting where sufficient data and balanced representation across categories are rarely available. By incorporating the reference information, the model is better equipped to learn nuanced patterns, handle unusual events, and produce more stable and accurate forecasts. The reference-guided mechanism compensates for the inherent lack of explicit semantic guidance in many time series. The effectiveness of this approach hinges on the design of both the retrieval and the integration of the references within the denoising process, necessitating careful consideration of embedding techniques, similarity metrics, and efficient attention mechanisms to maximize information utilization while minimizing computational overhead.
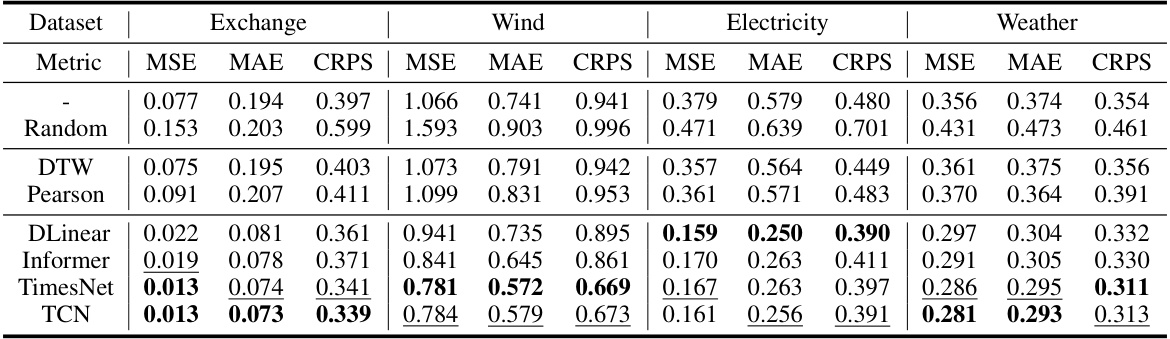
Dataset Construction Strategies#
Effective dataset construction is crucial for training robust time series forecasting models. Strategies must address inherent challenges like data scarcity and imbalance. One approach involves using the entire training set as a retrieval database, suitable when sufficient data exists. However, for imbalanced datasets, a stratified sampling technique is beneficial, ensuring representation from all categories. This tackles the issue of models overemphasizing frequently observed patterns at the expense of rare events. Preprocessing the database (e.g. creating embeddings) further enhances efficiency by enabling faster retrieval of relevant samples during training. Careful consideration of data characteristics and the model’s requirements is paramount for creating a database that optimally facilitates learning and accurate predictions. The chosen method should leverage available resources effectively to build a comprehensive and balanced dataset that avoids overfitting and biases.
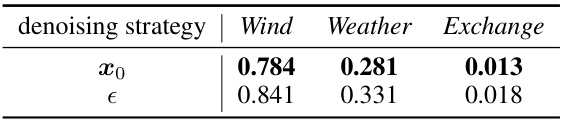
Model Ablation Study#
A model ablation study systematically removes components or features of a machine learning model to assess their individual contributions to the overall performance. This technique is crucial for understanding the model’s inner workings and identifying critical elements. By isolating the impact of each part, researchers can gain insight into the model’s strengths and weaknesses, and guide future model improvements. A well-designed ablation study should consider a range of different ablation strategies, carefully selecting components to remove or alter, and using appropriate metrics to evaluate performance. The results can inform decisions about model architecture, feature engineering, and hyperparameter tuning. It’s important to interpret ablation study results cautiously, as removing one component might unexpectedly impact the efficacy of others, highlighting the interconnectedness of model elements. A comprehensive study will demonstrate the robustness of findings by repeating the analysis with variations in experimental setups, and data splits to ensure reproducibility and generalizability.
Future Research#
Future research directions stemming from this Retrieval-Augmented Time series Diffusion model (RATD) could explore several promising avenues. Improving the retrieval mechanism is crucial; exploring more sophisticated similarity metrics beyond simple Euclidean distance, potentially incorporating temporal context or feature weighting, could significantly enhance reference selection. Another key area is developing more robust methods for handling imbalanced datasets. The current approach partially mitigates this issue, but more sophisticated techniques, such as data augmentation or cost-sensitive learning, warrant investigation. Further research could also focus on scaling RATD to handle even larger datasets and longer time series. This might necessitate exploring more efficient embedding techniques or distributed training strategies. Finally, extending RATD to incorporate other forms of side information, such as text descriptions or external knowledge graphs, promises to further boost the model’s accuracy and generalization capabilities, paving the way for more powerful and versatile time series forecasting models.
More visual insights#
More on figures
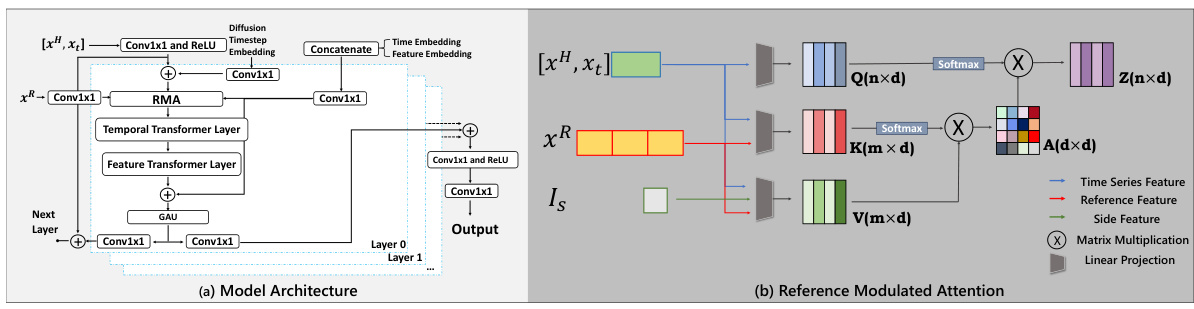
🔼 This figure shows the architecture of the proposed method’s core component: μθ, and its sub-component: Reference Modulated Attention (RMA). Part (a) illustrates the overall architecture of μθ, showing how time series features are processed through multiple layers (Conv1x1, ReLU, temporal and feature transformers, GAU) to generate the denoised time series. Part (b) details the RMA module, highlighting how it integrates three different kinds of features (time series feature, reference features, and side information) via matrix multiplication before feeding into the subsequent layers. This integration allows the model to effectively leverage references during the denoising process.
read the caption
Figure 3: The structure of μθ. (a) The main architecture of μθ is the time series transformer structure that proved effective. (b) The structure of the proposed RMA. We integrate three different features through matrix multiplication.
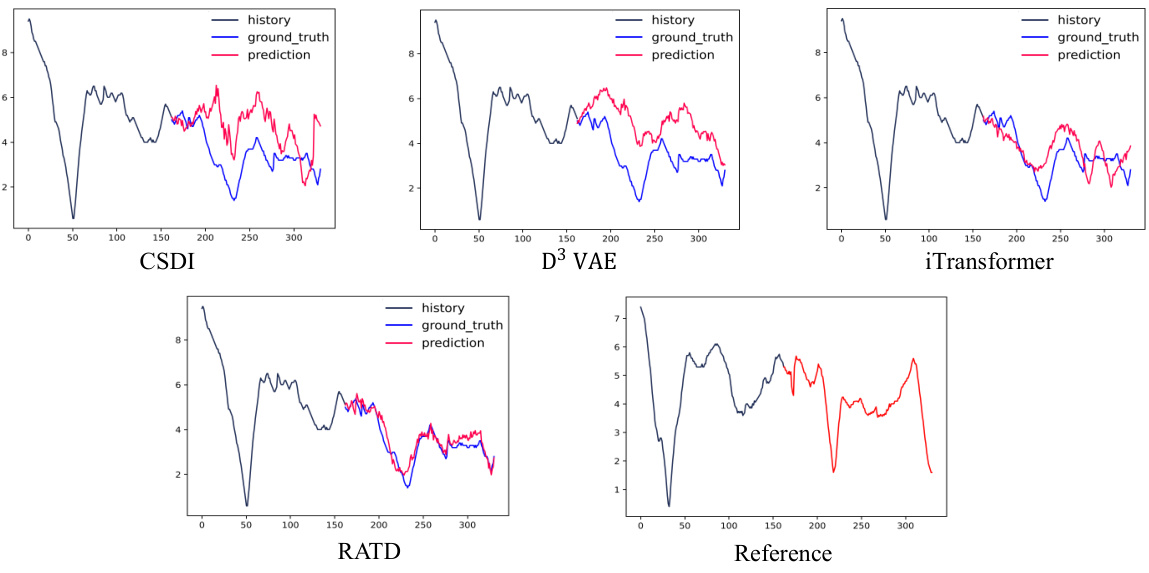
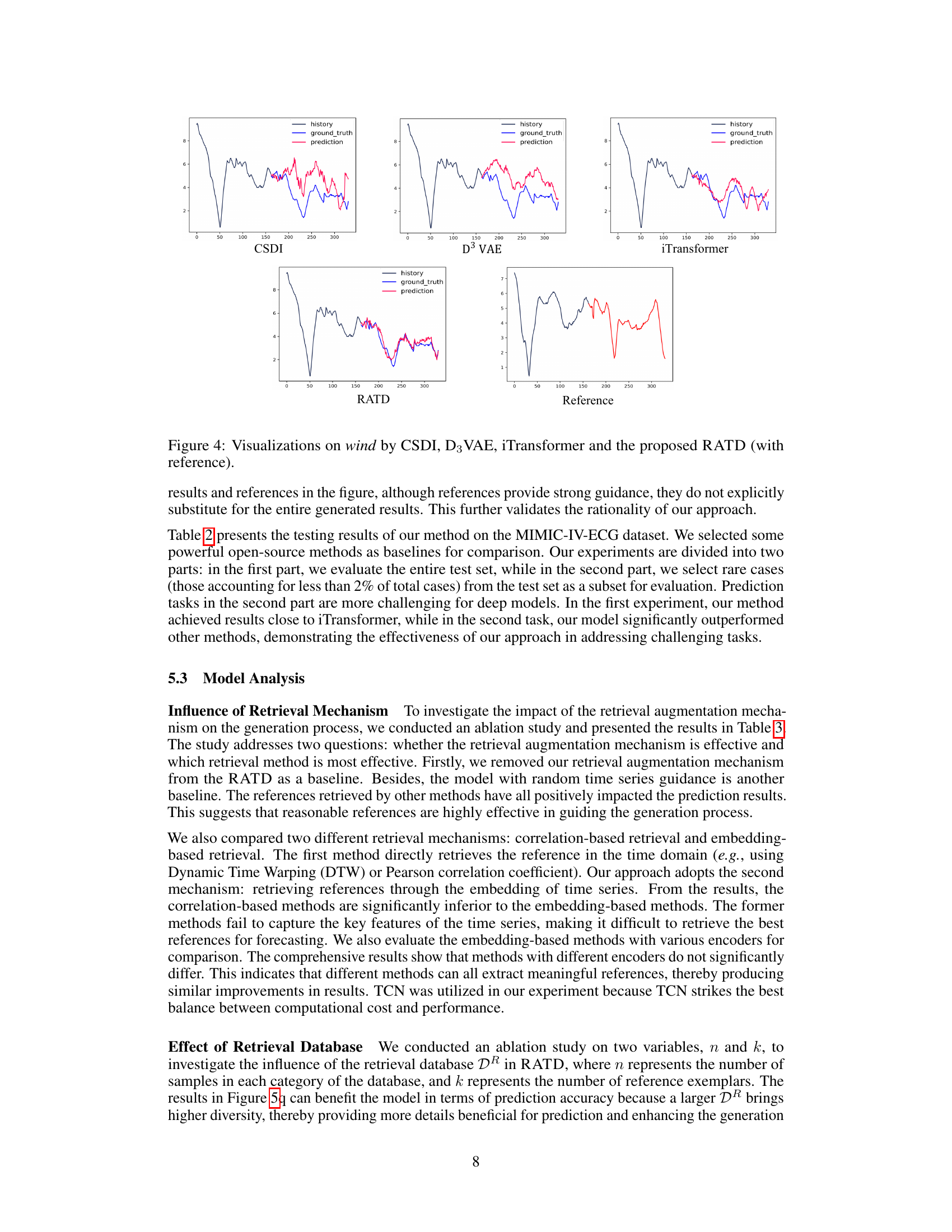
🔼 This figure compares the forecasting performance of four different models: CSDI, D3 VAE, iTransformer, and RATD on a wind dataset. Each model’s prediction is plotted alongside the ground truth and historical data. The figure showcases that RATD offers more accurate predictions, especially for long-term forecasting, outperforming other models.
read the caption
Figure 4: Visualizations on wind by CSDI, D3 VAE, iTransformer and the proposed RATD (with reference).
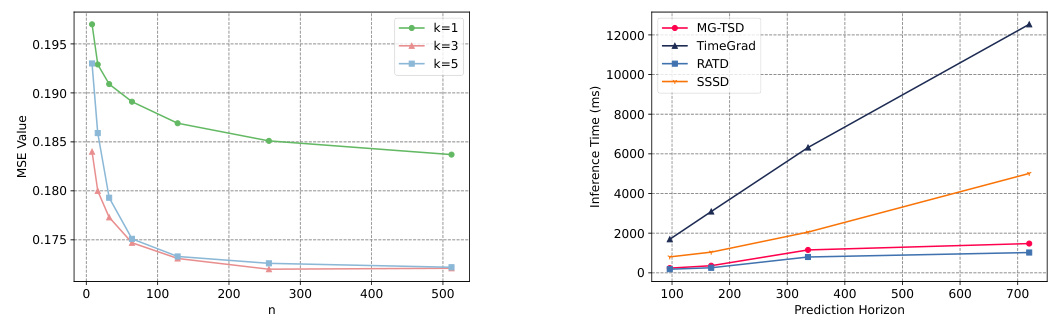
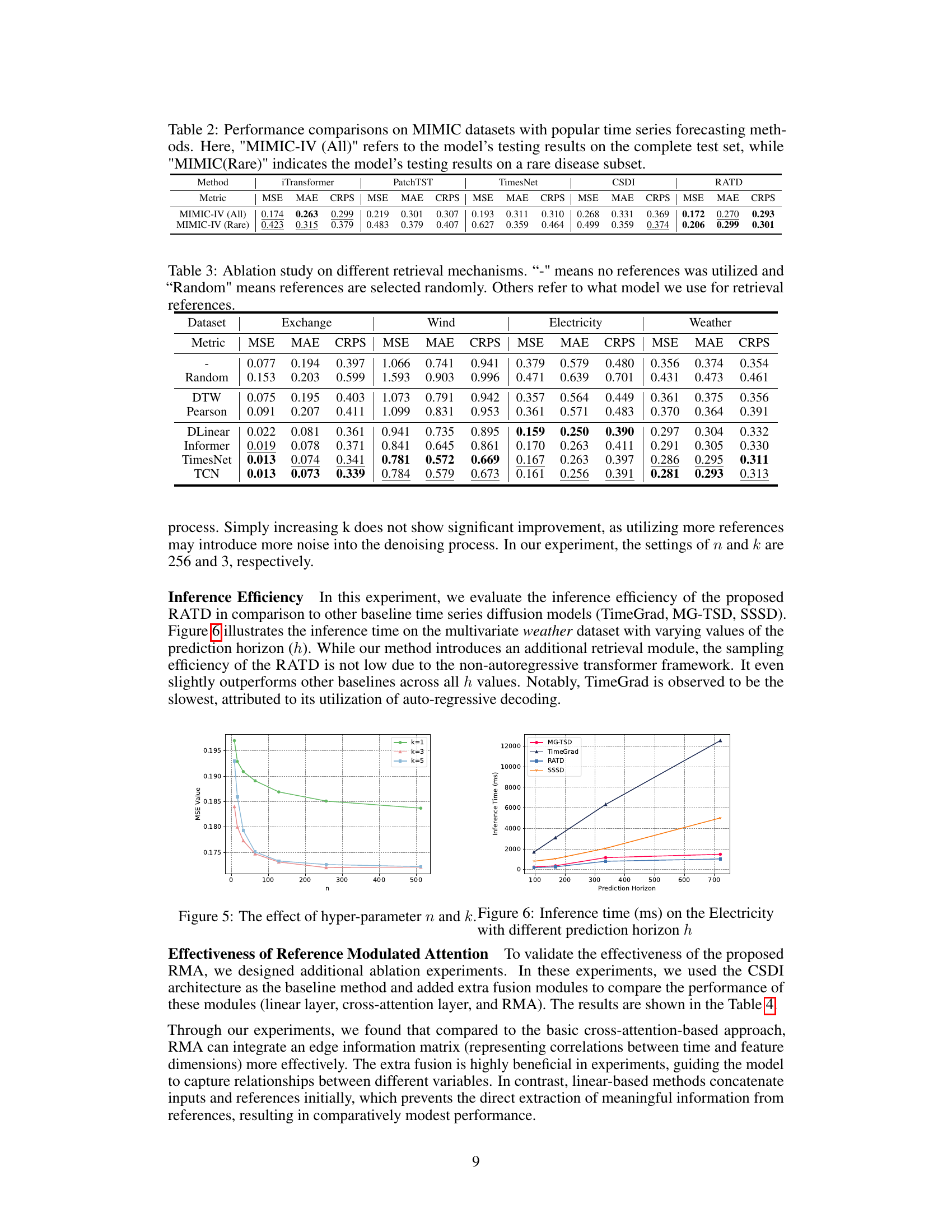
🔼 Figure 5 shows the impact of the hyperparameters n and k on the model’s performance. The left graph displays how the Mean Squared Error (MSE) changes as the number of samples (n) in each category of the database increases for different values of k (the number of retrieved references). The right graph shows the inference time in milliseconds (ms) for the Electricity dataset as the prediction horizon (h) increases for several different time series forecasting models: RATD, MG-TSD, TimeGrad, SSSD. The results demonstrate that carefully selecting these hyperparameters and using the proposed RATD model leads to more accurate and efficient predictions compared to baseline methods.
read the caption
Figure 5: The effect of hyper-parameter n and k. Figure 6: Inference time (ms) on the Electricity with different prediction horizon h
More on tables
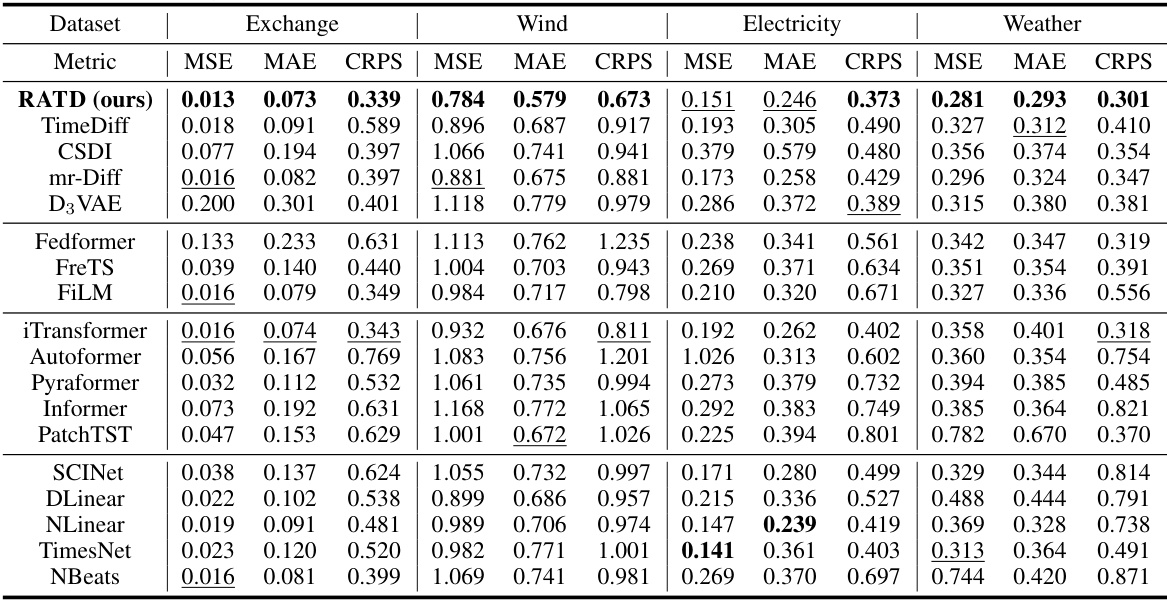
🔼 This table compares the performance of the proposed RATD model against several baseline models on four real-world datasets. The performance is evaluated using three metrics: Mean Squared Error (MSE), Mean Absolute Error (MAE), and Continuous Ranked Probability Score (CRPS). The best performing model for each metric and dataset is highlighted in bold, while the second-best is underlined. This allows for a clear comparison of the relative strengths and weaknesses of each model across different datasets and evaluation metrics.
read the caption
Table 1: Performance comparisons on four real-world datasets in terms of MSE, MAE, and CRPS. The best is in bold, while the second best is underlined.

🔼 This table compares the performance of RATD with other popular time series forecasting methods on the MIMIC-IV dataset. It presents results for the entire test set and a subset of rare cases (less than 2% of the total). The ‘Rare’ subset helps evaluate the model’s ability to handle complex, less-frequent data.
read the caption
Table 2: Performance comparisons on MIMIC datasets with popular time series forecasting methods. Here, 'MIMIC-IV (All)' refers to the model’s testing results on the complete test set, while 'MIMIC(Rare)' indicates the model’s testing results on a rare disease subset.
🔼 This table presents a comparison of the proposed RATD model against various baseline methods across four real-world datasets. The performance is evaluated using three metrics: Mean Squared Error (MSE), Mean Absolute Error (MAE), and Continuous Ranked Probability Score (CRPS). The best performing model for each metric and dataset is highlighted in bold, with the second-best underlined. This allows for a comprehensive comparison of the model’s effectiveness against existing state-of-the-art methods.
read the caption
Table 1: Performance comparisons on four real-world datasets in terms of MSE, MAE, and CRPS. The best is in bold, while the second best is underlined.

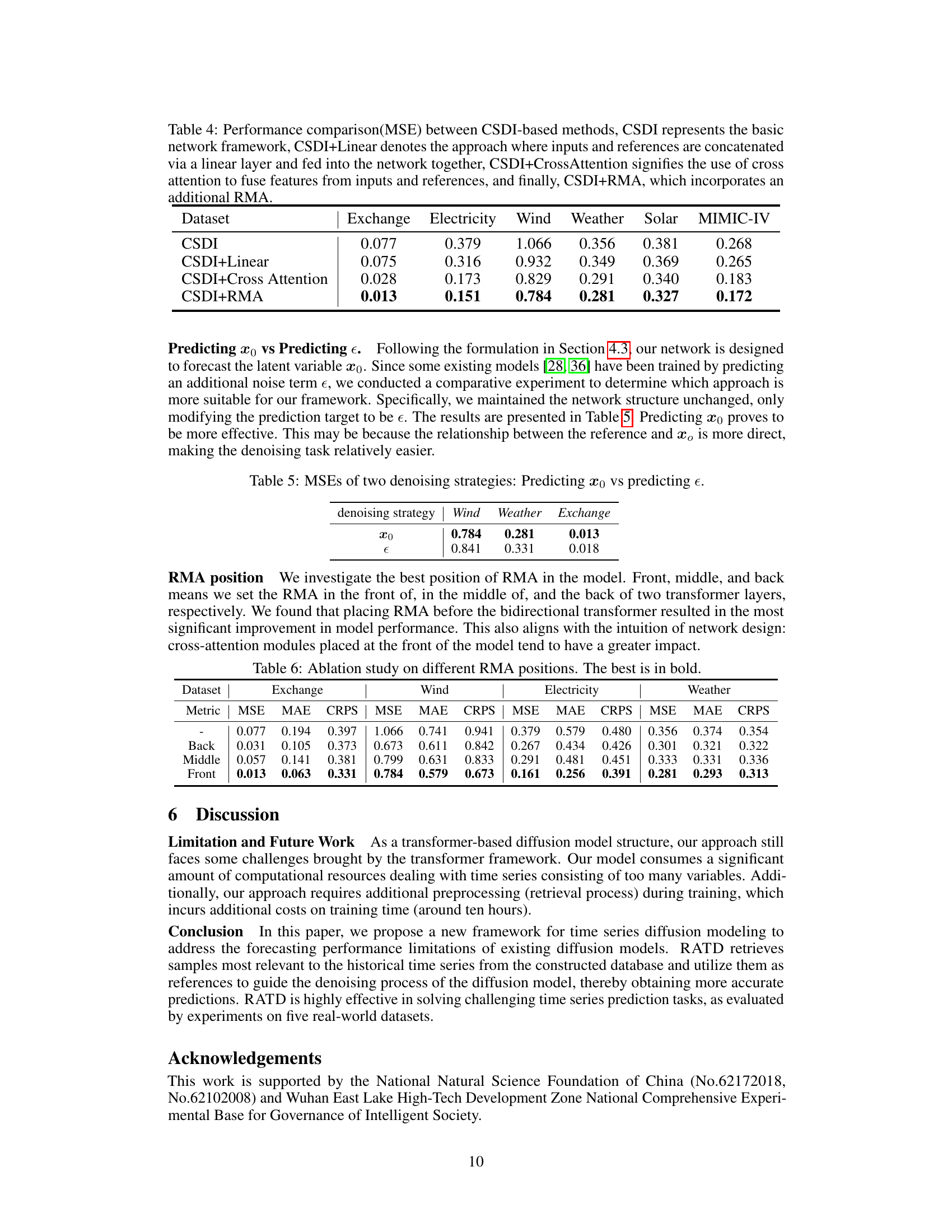
🔼 This table presents a comparison of Mean Squared Error (MSE) achieved by different models on various datasets. The models compared are CSDI (baseline), CSDI+Linear (adding linear concatenation of inputs and references), CSDI+Cross Attention (adding cross-attention fusion), and CSDI+RMA (the proposed method incorporating the Reference Modulated Attention module). Lower MSE values indicate better performance.
read the caption
Table 4: Performance comparison(MSE) between CSDI-based methods, CSDI represents the basic network framework, CSDI+Linear denotes the approach where inputs and references are concatenated via a linear layer and fed into the network together, CSDI+CrossAttention signifies the use of cross attention to fuse features from inputs and references, and finally, CSDI+RMA, which incorporates an additional RMA.
🔼 This table presents a comparison of the performance of the proposed RATD model against several baseline time series forecasting methods across four real-world datasets: Exchange, Wind, Electricity, and Weather. The performance is evaluated using three metrics: Mean Squared Error (MSE), Mean Absolute Error (MAE), and Continuous Ranked Probability Score (CRPS). The best performing model for each metric and dataset is highlighted in bold, while the second-best is underlined. This allows for a direct comparison of the different models’ accuracy and uncertainty quantification capabilities across various datasets.
read the caption
Table 1: Performance comparisons on four real-world datasets in terms of MSE, MAE, and CRPS. The best is in bold, while the second best is underlined.

🔼 This table presents the ablation study results on the impact of different RMA positions (front, middle, and back) on the model’s performance. The results are presented in terms of MSE, MAE, and CRPS metrics across four datasets (Exchange, Wind, Electricity, and Weather). The best performing RMA position for each dataset and metric is shown in bold, highlighting the optimal placement of the RMA module within the network architecture for enhanced time series forecasting accuracy.
read the caption
Table 6: Ablation study on different RMA positions. The best is in bold.
Full paper#