↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current machine learning heavily relies on large datasets, unlike natural learning processes which learn efficiently from limited, readily available information. This paper addresses this gap by proposing a nature-inspired approach. The existing backpropagation algorithm, widely used for training neural networks, suffers from limitations like the requirement for full data and the lack of biological plausibility.
The core contribution is a novel spatiotemporal local algorithm, inspired by optimal control theory and principles from theoretical physics. This algorithm performs online learning, processing information locally and sequentially without needing vast data collections. It also naturally integrates temporal information and overcomes the limitations of backpropagation, proving to be particularly effective for tasks such as lifelong learning with long video streams. This study makes a significant contribution by bridging the gap between artificial and natural learning processes, offering a more biologically plausible and efficient learning framework.
Key Takeaways#
Why does it matter?#
This paper is important because it challenges the conventional reliance on large datasets in machine learning by proposing a novel spatiotemporal local algorithm inspired by natural learning processes. This opens new avenues for online learning, particularly in scenarios with limited data or long video streams. It also addresses the biological implausibility of backpropagation and provides a novel perspective on the long-standing debate on biological plausibility.
Visual Insights#

This figure shows the result of applying the proposed algorithm to track a complex, unpredictable signal. The blue line represents the output of the neural network attempting to follow the target signal (orange dashed line). The parameters used in this experiment included 5 neurons, an accuracy term (q) of 100, a weight regularization term (rw) of 1, and a derivative of the weight term (r) of 0.1. This experiment demonstrates the algorithm’s ability to track a signal that is difficult to predict due to its highly variable nature.
In-depth insights#
Spatiotemporal Locality#
Spatiotemporal locality, a concept central to biologically inspired learning, is explored in the context of overcoming limitations of traditional backpropagation algorithms. The core idea is to constrain learning processes to respect the local flow of information in both space (connections between neurons) and time (sequential processing of data). This contrasts with backpropagation’s assumption of instantaneous signal propagation across the entire network. The paper proposes a novel algorithm based on Hamiltonian dynamics that naturally incorporates this locality, suggesting that limiting the scope of each update to only immediately neighboring neurons and recent inputs leads to more biologically plausible and efficient learning. This local propagation approach is contrasted with the global updates of backpropagation, suggesting that its infinite-speed assumption is a significant deviation from biological systems. The theoretical implications of this spatiotemporal constraint are analyzed in detail, and the paper demonstrates a computational model capable of achieving online learning with the desired locality. The discussion of spatiotemporal locality challenges the conventional view of machine learning algorithms, emphasizing the importance of incorporating biologically inspired principles for improved efficiency and robustness. A key argument focuses on how this approach addresses the update locking and infinite signal propagation challenges of backpropagation, thereby producing a more realistic model of neural computation.
Hamiltonian Learning#
Hamiltonian learning, a fascinating concept, blends the elegance of Hamiltonian mechanics with the power of machine learning. It offers a novel perspective on optimization by framing the learning process as a continuous-time optimal control problem, leveraging Hamiltonian equations to govern the dynamics of both the system’s state and its parameters. The core idea lies in representing the learning objective as a functional to be minimized, where the system’s evolution is shaped by Hamiltonian equations. This framework elegantly connects learning with fundamental physical principles, promising a deeper understanding of the learning process itself. One compelling aspect is the potential for spatiotemporal locality, directly addressing limitations of traditional backpropagation-based methods that struggle with issues of update locking and infinite signal speed. This locality aligns Hamiltonian learning with biological learning mechanisms observed in nature. However, a significant challenge lies in handling boundary conditions inherent in the Hamiltonian formulation, which often clashes with the desirable causal and online nature of learning. Strategies such as Hamiltonian sign-flip or time reversal of the costate offer intriguing pathways to overcome these boundary condition issues, but demand further investigation. Overall, Hamiltonian learning holds immense potential for creating more efficient, biologically-plausible, and theoretically grounded machine learning algorithms, but its full potential will require substantial future research to overcome current limitations.
Pre-algorithmic Learning#
The concept of “Pre-algorithmic Learning” suggests a paradigm shift in machine learning, moving away from the traditional algorithmic approaches. It emphasizes learning as a fundamental process in nature, occurring organically and locally without explicit programming. This approach focuses on mimicking natural learning mechanisms which emphasize the interplay between data representation and learning, respecting spatiotemporal locality. Instead of relying on large datasets, it proposes learning from continuous online processing of environmental information, mirroring the way biological systems learn. The core idea is to define “laws of learning” based on principles from theoretical physics, reducing to backpropagation as a limiting case and offering an alternative for online machine learning.
Backprop as a Limit#
The concept of “Backprop as a Limit” suggests that backpropagation, a cornerstone of modern deep learning, can be viewed as an extreme case of a more general, biologically plausible learning algorithm. This more general algorithm emphasizes spatiotemporal locality, meaning that learning is constrained by the speed of information propagation within a network, unlike backpropagation which assumes instantaneous signal transmission. The research likely explores how this spatiotemporal model reduces to backpropagation when certain parameters (such as the speed of propagation) approach infinity. This framing offers a valuable bridge between the efficiency of backpropagation and the biologically realistic nature of local learning. The analysis might involve deriving the spatiotemporal algorithm using principles from optimal control theory or Hamiltonian dynamics, showing its convergence to backpropagation under specific limiting conditions. This work potentially provides insights into more biologically plausible and energy-efficient learning methods, which could lead to significant advancements in AI and our understanding of neural computation. The ’limit’ aspect underscores that backpropagation is an approximation that might be improved upon by considering the inherent limitations of physical information flow. By providing a better model of biologically inspired learning, we might develop algorithms that generalize better, require less data, and exhibit greater robustness. It potentially offers a foundation for energy-efficient artificial neural systems with more explainable learning characteristics.
Boundary Condition Issue#
The Boundary Condition Issue in the paper centers on the inherent non-locality introduced by the global nature of the cost function in optimal control theory. Hamilton’s equations, while locally defined, are coupled across time via boundary conditions at both the beginning and end of the learning process. This contradicts the desired spatiotemporal locality sought by the proposed algorithm, limiting the online and truly local learning that mimics natural processes. The paper highlights that standard numerical solutions, by relying on these global boundary conditions, fail to achieve the desired causality, necessitating innovative approaches. Time reversal methods, proposed as a solution, present ways to transform the problem into a form that allows a causal, local, iterative solution. By addressing the boundary condition issue, the authors pave the way for a fully online, truly local learning algorithm inspired by biological systems.
More visual insights#
More on figures

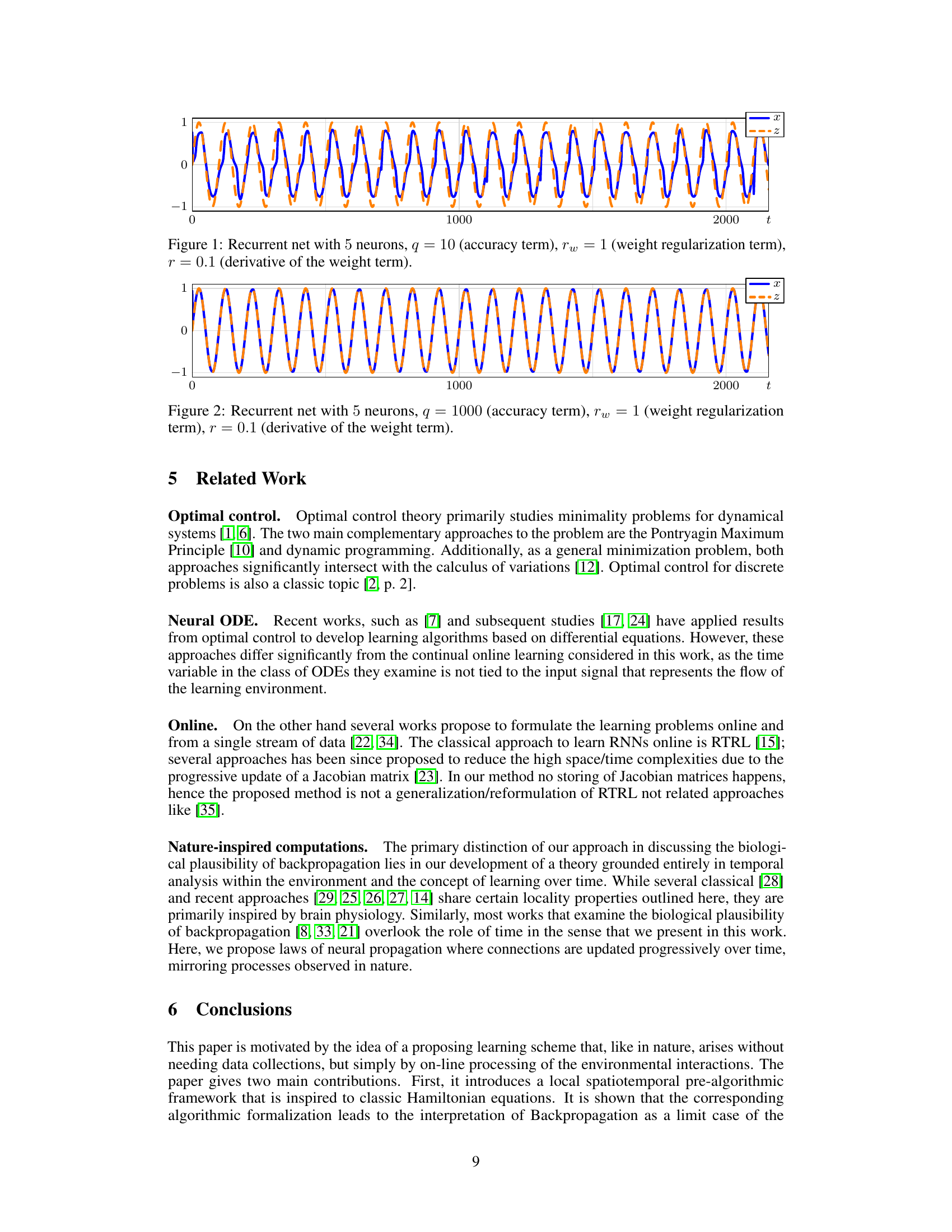
This figure shows the result of applying the proposed recurrent neural network model to track a sinusoidal signal. The blue line represents the output of the network (x), while the orange dashed line represents the target signal (z). The parameters q, rw, and r control the accuracy of the approximation, the weight regularization, and the derivative of the weight term respectively. The plot demonstrates the network’s ability to track the target signal with a relatively small number of neurons and chosen parameters.

This figure shows the result of applying the Hamiltonian Sign Flip method to track a highly unpredictable signal. The signal is composed of patching intervals with cosine functions with constants and is purposely generated to be hard to predict. The network uses 5 neurons. The parameters used are: accuracy term (q) = 100, weight regularization term (rw) = 1, derivative of the weight term (r) = 0.1. The plot displays the tracked signal (x, blue line) against the target signal (z, orange dotted line). The figure demonstrates the network’s ability to track the signal despite its high unpredictability.

This figure shows the evolution of both the Lagrangian and Hamiltonian functions over time for a specific tracking experiment (Experiment 3). It illustrates the energy exchange dynamics during the learning process. The Lagrangian represents the cost function being minimized, while the Hamiltonian reflects the system’s overall energy. The plot visually represents how the system navigates the energy landscape to achieve the tracking goal.

This figure shows the architecture of the recurrent neural network used in the experiments of Section 4.2 of the paper. It’s a fully connected graph with five neurons (nodes) and numerous weighted connections (edges) between them. The neurons are labeled as 1 through 5. Each edge is annotated with a weight (Wij). One neuron is highlighted in red, signifying that it serves as the output neuron and is constrained to follow a reference (or target) signal during the experiments. This network is used to validate the Hamiltonian Sign Flip (HSF) strategy discussed in the paper, aiming to improve online learning by addressing issues with boundary conditions in the Hamiltonian equations.
Full paper#