↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Traditional camera pose synchronization methods often rely on pairwise relationships, resulting in limitations due to noisy and incomplete data. This paper introduces a novel approach that leverages higher-order interactions between three or more cameras by employing block trifocal tensors. These tensors provide richer geometric information, overcoming the challenges posed by pairwise methods.
The proposed method introduces a novel synchronization algorithm based on the low multilinear rank property of the block trifocal tensor. This algorithm uses a higher-order singular value decomposition (HOSVD) to enforce the low-rank constraint and iteratively refines scale estimates. Experimental results on real-world datasets demonstrate a significant improvement in location estimation accuracy compared to the state-of-the-art global synchronization techniques. The work also provides a rigorous theoretical foundation demonstrating the sufficiency of the low-rank constraint for camera recovery in noiseless conditions.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in computer vision and related fields because it introduces a novel approach to camera pose synchronization using higher-order interactions (trifocal tensors), leading to significant improvements in accuracy and efficiency compared to traditional pairwise methods. It opens up new research avenues for exploiting higher-order relationships in various synchronization problems and provides a robust, scalable algorithm that addresses the challenges of noisy and incomplete data. The work also provides strong theoretical insights into the structure of the block trifocal tensor, demonstrating its low multilinear rank and proving its sufficiency for camera recovery in the noiseless case. This makes a significant contribution to the advancement of Structure from Motion techniques and broader synchronization problems.
Visual Insights#
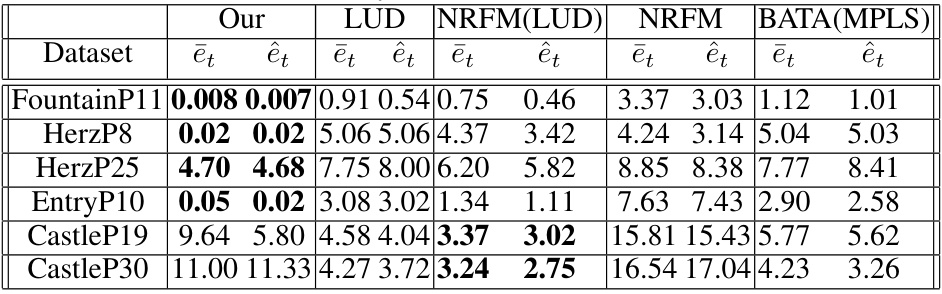
The figure shows a bar chart comparing the mean and median translation errors of different structure-from-motion algorithms on six datasets from the EPFL dataset. The algorithms compared are the proposed method, LUD, NRFM (initialized with LUD), NRFM (randomly initialized), and BATA (initialized with MPLS). Each bar represents the error for a specific dataset, and the chart illustrates the relative performance of each algorithm across the datasets.
This table presents the mean and median rotation and translation errors for the EPFL dataset. The results are compared for the proposed method (Our) against LUD, NRFM (initialized with LUD), NRFM (initialized randomly), and BATA (initialized with MPLS).
In-depth insights#
Block Trifocal Tensor#
The concept of a ‘Block Trifocal Tensor’ represents a significant advancement in multi-view geometry, offering a powerful tool for camera pose estimation. It leverages the inherent properties of trifocal tensors, which encapsulate the projective relationships between three views, to build a higher-order structure. This block structure enables the simultaneous processing of multiple trifocal tensors, thereby addressing limitations of pairwise-based methods. The key innovation lies in the observation and exploitation of the low multilinear rank of this block tensor. This low rank is not only theoretically elegant, but also computationally advantageous, leading to efficient synchronization algorithms. By enforcing this low-rank constraint, the method can accurately recover camera locations and orientations, even in the presence of noise and missing data. Further, this framework provides a foundation for overcoming challenges associated with traditional techniques and offers significant potential for improving the accuracy and scalability of structure-from-motion pipelines.
Tucker Factorization#
Tucker factorization, a higher-order generalization of singular value decomposition (SVD), plays a crucial role in the paper by enabling the analysis of the block trifocal tensor. The factorization reveals a low multilinear rank, implying inherent structure within the tensor that is independent of the number of cameras. This low-rank property forms the basis for a novel synchronization algorithm. The algorithm exploits the inherent low-rank structure for efficiently and accurately estimating camera poses. By using Tucker decomposition, the algorithm avoids the computational burden of dealing with the full tensor directly, making it efficient for real-world applications with a large number of cameras. The low rank is a key theoretical contribution, demonstrating a fundamental constraint that facilitates efficient and accurate camera pose recovery. Furthermore, the proof that the low rank suffices for camera retrieval in the noiseless setting is a significant theoretical result. This highlights the power of higher-order tensor analysis in solving complex computer vision problems.
HOSVD-HT Method#
The HOSVD-HT method, a core contribution of the research paper, presents a novel approach to handling the challenges of synchronizing block trifocal tensors. It leverages the Tucker factorization of the block tensor, revealing its low multilinear rank. This low rank is then exploited to develop an algorithm that iteratively refines estimates of trifocal tensors by enforcing this rank constraint. A key aspect of the method involves the use of higher-order singular value decomposition (HOSVD), but with a critical modification: a hard threshold is applied to the singular values, allowing for the effective truncation of the tensor. This truncation mitigates noise effects, crucial for real-world datasets. The method further incorporates an iterative refinement process, incorporating the rank-truncated results back into subsequent estimations to improve accuracy and address incomplete data. The hard thresholding parameter is a key aspect of the HOSVD-HT method and must be carefully tuned to achieve an appropriate balance between noise reduction and information retention, which could greatly affect the algorithm’s overall performance. The method’s efficiency is enhanced through the use of randomized SVD techniques for handling the large-scale tensors encountered in real-world applications.
Synchronization Alg.#
The heading ‘Synchronization Alg.’ suggests a section detailing algorithms designed to achieve synchronization, likely within a computer vision or related field. A thoughtful analysis would expect this section to explore various approaches, comparing their strengths and weaknesses. Key aspects likely covered include the mathematical foundations underpinning the synchronization process, such as geometric constraints or algebraic formulations. Different algorithm types—iterative, global, or incremental—would be discussed, and their computational complexities analyzed. Performance metrics are also crucial: accuracy of pose estimations (location and orientation), robustness to noise, and scalability with respect to the number of data points or sensors should be presented and potentially compared with existing methods. The section might also delve into specific applications of these algorithms, along with discussions of potential limitations or challenges encountered in real-world scenarios. A key focus is likely on how the choice of algorithm impacts the overall efficiency and accuracy of the system in achieving synchronization.
Future Works#
Future research directions stemming from this work could explore several promising avenues. Extending the theoretical framework to handle quadrifocal and higher-order tensors would provide a more robust and comprehensive representation of multi-view geometry, potentially leading to even more accurate synchronization. Developing more efficient algorithms to handle the computational complexity associated with higher-order tensors is crucial for scalability. This might involve exploring different tensor decomposition methods or leveraging parallel computing techniques. Improving the robustness of the algorithm to noise and outliers is another key area for future work. This could be achieved by incorporating robust estimation techniques or developing more sophisticated outlier detection methods. Finally, applying the proposed method to other applications of synchronization, such as SLAM and community detection, would demonstrate its broader applicability and potential for impacting these fields.
More visual insights#
More on figures

This figure compares the translation error performance of six different structure-from-motion algorithms on the EPFL dataset. The algorithms are: the proposed method, NRFM (initialized with LUD), LUD, NRFM (initialized randomly), and BATA (initialized with MPLS). The comparison is shown using both mean and median translation errors across six different scenes within the dataset (FP11, HZP8, HZ25, EN10, CS19, CS30). The results visually demonstrate the proposed method’s superior performance compared to other algorithms for most of the scenes in terms of both mean and median translation errors.

This figure compares the translation error of the proposed method against three state-of-the-art methods (LUD, NRFM initialized with LUD, and NRFM with random initialization) and BATA initialized with MPLS across six different datasets from the EPFL dataset. The mean and median translation errors are displayed for each method and dataset, showcasing the relative performance of each approach in terms of location estimation accuracy.
More on tables

This table presents a comparison of rotation errors for the EPFL dataset between the proposed method and two other state-of-the-art methods (LUD and BATA initialized with MPLS). The mean and median rotation errors (in degrees) are shown for each method and dataset.

This table presents the results of translation error comparison for Photo Tourism datasets. It shows the mean and median translation errors (ēt and êt respectively) for different datasets using various methods: the proposed approach, LUD, and NRFM (initialized with LUD and randomly). The table includes the number of cameras (n) after downsampling, the percentage of observed blocks, and the results from the BATA method (initialized with MPLS).
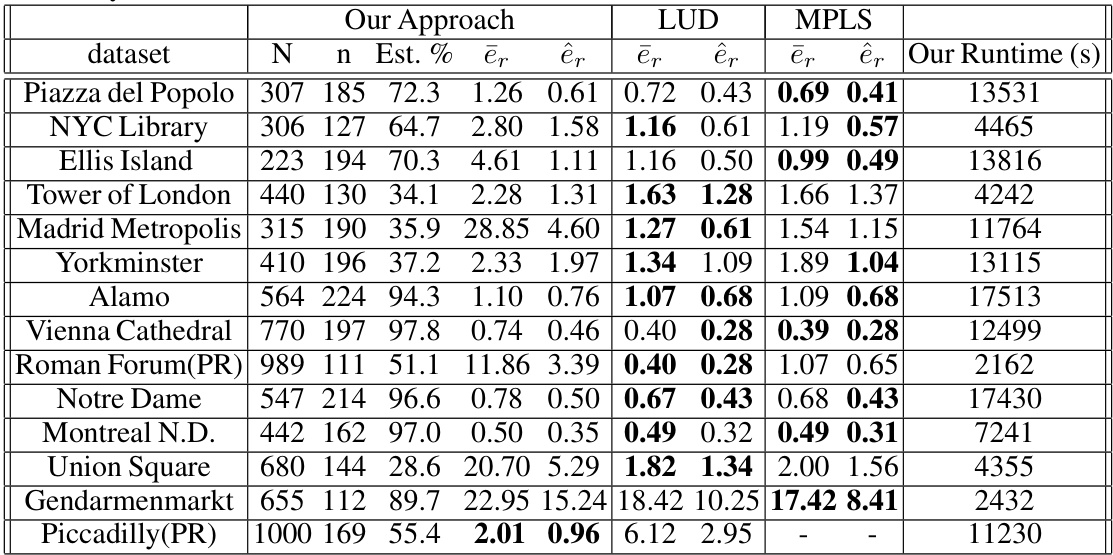
This table presents a comparison of location estimation errors for different Structure from Motion (SfM) methods on the Photo Tourism dataset. The methods compared include the proposed approach, LUD, NRFM initialized with LUD, NRFM with random initialization, and BATA initialized with MPLS. The table shows the mean and median translation errors for each method, along with the number of cameras (n), the percentage of observed blocks (Est. %), and the runtime of the proposed method. Note that for the Piccadilly and Roman Forum datasets, downsampling was performed to match the number of cameras used by the two-view methods.
Full paper#



















