↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Federated Reinforcement Learning (FRL) tackles the challenge of training RL agents across distributed devices without compromising data privacy. Existing FRL methods struggle with multi-task scenarios, where each agent has a unique reward function, and decentralized settings, where agents only communicate with neighbors. This limits scalability and the ability to find optimal global policies.
This work presents novel federated natural policy gradient (NPG) and actor-critic (NAC) methods designed for multi-task learning in fully decentralized environments. These methods leverage gradient tracking for accurate global Q-function estimation, and they are theoretically proven to converge quickly, even with limited information exchange between agents and function approximation errors. The findings significantly advance the understanding and efficiency of FRL in complex multi-task settings.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in federated and multi-task reinforcement learning. It provides the first-ever near dimension-free global convergence guarantees for such settings, a significant advancement. This opens avenues for more efficient and robust algorithms in decentralized collaborative decision-making scenarios, impacting various applications like healthcare and smart cities.
Visual Insights#
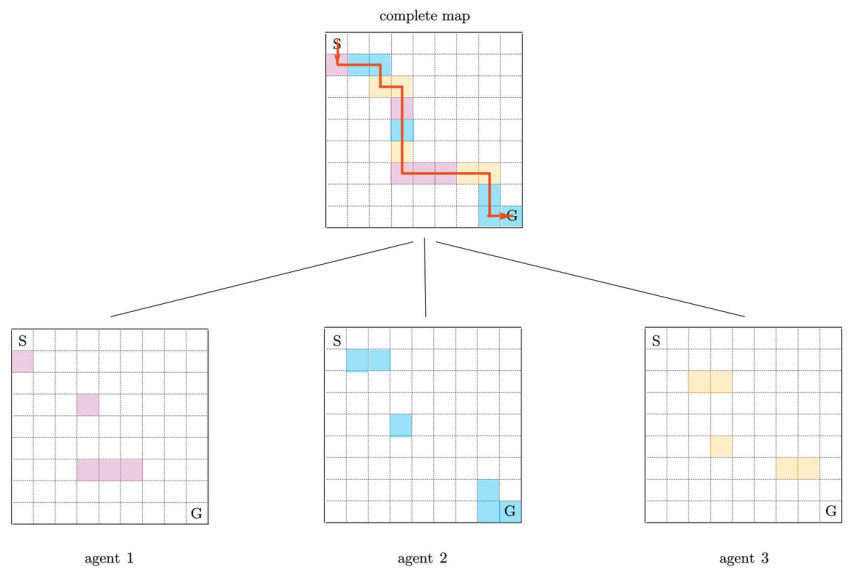
This figure illustrates the setup of a multi-agent reinforcement learning experiment in a gridworld environment. The overall goal is for multiple agents to collaboratively learn a single policy that guides them along a specified path from a starting point (S) to a goal (G). However, each agent only has access to a limited, partial view of the entire gridworld. The figure shows the complete map with the optimal path, and the partitioned views of the map seen by three individual agents. The shaded squares within each agent’s view represent locations where the agent receives a reward of 1 for successfully reaching them; otherwise, the reward is 0. This setup models scenarios where information is distributed and decentralized, making it an ideal testing ground for federated reinforcement learning algorithms.

This table presents the iteration complexities for both centralized and federated NPG methods to achieve an ε-accurate solution for the vanilla and entropy-regularized multi-task reinforcement learning problems. The table shows how the iteration complexities depend on various factors, including the number of agents (N), the regularization parameter (τ), the spectral radius of the network (σ), the discount factor (γ), the size of the action space (|A|), and the learning rate (η). For the federated method, the complexities reduce to their centralized counterparts when the network is fully connected (σ = 0).
In-depth insights#
Fed Multi-task RL#
Federated multi-task reinforcement learning (Fed Multi-task RL) presents a novel challenge at the intersection of distributed systems and machine learning. It addresses the need for multiple agents to collaboratively learn a shared optimal policy without directly sharing their private data, each agent having its unique reward function reflecting a specific task. This decentralized approach is crucial in scenarios with data privacy concerns, such as healthcare or finance, and allows for scalability across a network of geographically distributed agents. Key challenges include balancing local learning with global policy optimization, handling non-identical reward functions, and ensuring convergence and efficiency under communication constraints. The theoretical analysis of Fed Multi-task RL is complex, involving techniques from decentralized optimization and reinforcement learning, and often requires stringent assumptions to establish convergence guarantees. Practical application necessitates addressing the impacts of network topology, communication delays, and the computational cost associated with decentralized learning. Robust algorithms that demonstrate near-optimal performance in realistic scenarios remain a subject of ongoing research.
NPG & NAC Methods#
The research paper section on “NPG & NAC Methods” likely details natural policy gradient (NPG) and natural actor-critic (NAC) algorithms within the context of federated multi-task reinforcement learning. NPG is a policy optimization method that uses natural gradients to update the policy parameters, offering faster convergence compared to standard policy gradient approaches. The discussion probably covers the theoretical properties of NPG in a federated and multi-task setting, potentially including convergence rates and sample complexity analysis. NAC extends NPG by using function approximation and stochastic policy evaluation, making it more practical for complex environments. The section likely presents federated versions of these algorithms, focusing on how to address the challenges of distributed computation and communication constraints while ensuring that each agent only accesses and shares local data according to a prescribed network topology. A key aspect of the analysis would be to show the algorithms’ ability to achieve global optimality while only using local information. The effectiveness and robustness of the federated NPG and NAC methods are assessed and compared, considering factors like network structure and the accuracy of policy evaluation. The authors likely provide theoretical convergence guarantees and, ideally, experimental results to validate the effectiveness of their proposed algorithms in realistic scenarios.
Convergence Rates#
Analyzing convergence rates in a research paper requires a nuanced understanding of the methodology and theoretical underpinnings. A key aspect is identifying the type of convergence: does the algorithm converge in probability, almost surely, or in expectation? The paper should clearly define the metric used to measure convergence (e.g., distance to optimum, error rate, or suboptimality gap) and the rate at which this metric decreases. Understanding the dependence of convergence rates on problem parameters (e.g., dimension of state-action space, discount factor, network size) is vital. Faster convergence rates that are near dimension-free (i.e., independent of the size of the state-action space) are highly desirable and often signify superior algorithms. The robustness of convergence rates to various factors, including imperfect information sharing, function approximation errors, and stochastic policy evaluation, should be investigated. The presence of tight bounds (upper and lower) on the convergence rates demonstrates rigorous analysis, enabling a more precise comparison across algorithms and facilitating practical implementation. Claims of linear convergence suggest exceptionally fast convergence, whereas sublinear rates, while slower, might still be acceptable depending on the application. Overall, evaluating the convergence rates necessitates a careful examination of both theoretical guarantees and empirical results, verifying that theory and practice align closely.
Sample Complexity#
The concept of sample complexity is crucial in evaluating the efficiency of reinforcement learning algorithms, especially within the context of federated multi-task settings. Lower sample complexity signifies that the algorithm requires fewer data samples to achieve a desired level of performance. In federated learning, this aspect is critical because data is decentralized across multiple agents and communication bandwidth might be limited. The paper likely analyzes how the sample complexity scales with respect to different factors such as the size of the state-action space, the number of tasks (or agents), the network topology of the communication graph, and the accuracy level desired. A key insight might be the establishment of near dimension-free sample complexity bounds, indicating that the required number of samples remains relatively insensitive to the dimensionality of the problem. The impact of function approximation and stochastic policy evaluation on sample complexity is another significant focus area. It investigates how the approximation error or the variance of the policy evaluation impacts the number of samples necessary for convergence. This analysis offers critical insights into the practical efficiency and scalability of the proposed federated multi-task reinforcement learning algorithms.
Future Directions#
Future research directions could explore generalizing the federated multi-task RL framework to enable personalized policy learning in a shared environment. This would involve developing algorithms that can adapt to the unique characteristics and preferences of individual agents while still maintaining the benefits of collaborative learning. Another promising avenue is investigating the impact of different network topologies and communication protocols on the convergence and performance of federated multi-task RL algorithms. This would require a more in-depth understanding of the trade-offs between communication efficiency and accuracy in decentralized settings. Finally, developing sample-efficient algorithms for federated multi-task RL with function approximation and stochastic policy evaluation remains a significant challenge. Addressing these challenges would require advances in both reinforcement learning theory and decentralized optimization techniques. The robustness of the proposed methods to various forms of imperfect information sharing (e.g., noisy communication, delayed updates) should be analyzed. Ultimately, a key aspect is extending the current theoretical analysis to more complex and realistic multi-agent environments involving continuous state and action spaces, partial observability, and non-stationary dynamics.
More visual insights#
More on figures
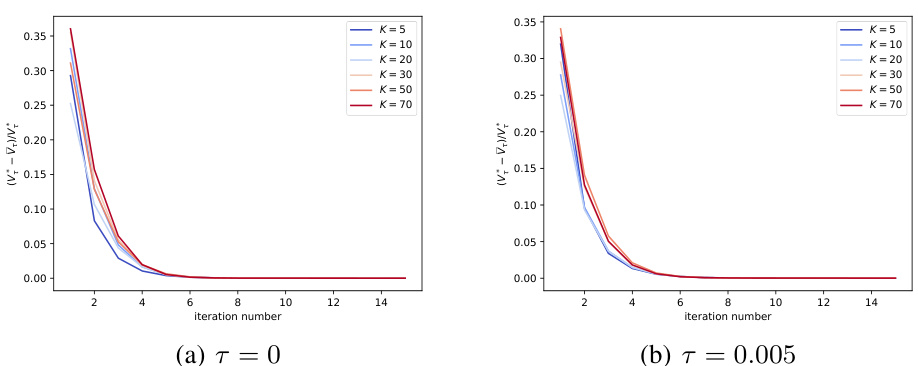
This figure shows the convergence speed of vanilla and entropy-regularized Federated Natural Policy Gradient (FedNPG) methods for different map sizes (K). The results indicate that both methods converge to the optimal value function within a few iterations, and the convergence speed remains consistent across different map sizes. This suggests that the performance of FedNPG is largely insensitive to the size of the state-action space.

This figure shows the impact of the number of agents (N) on the convergence speed of the FedNPG algorithm. The experiment is conducted on GridWorld environments with different map sizes (K=10, 20, 30). The results indicate that increasing the number of agents leads to a slower convergence speed, while the map size does not significantly affect the convergence speed.

This figure shows the impact of communication network topology on the performance of the federated natural policy gradient (FedNPG) algorithm. Two scenarios are compared: random weights and equal weights. The results demonstrate that the convergence speed improves with an increase in the number of neighbors and that FedNPG performs better with equal weights.
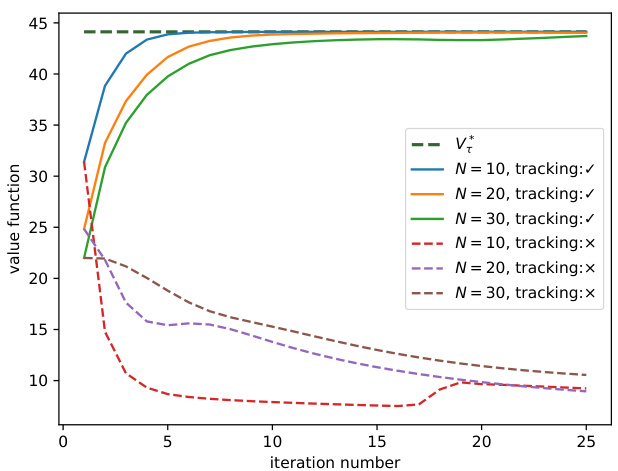
This figure compares the performance of FedNPG with and without the Q-tracking technique. The x-axis represents the number of iterations, and the y-axis represents the value function. Multiple lines are plotted, each showing the convergence for a different number of agents (N=10, 20, 30). Solid lines represent runs using FedNPG (with Q-tracking), and dashed lines represent runs without Q-tracking. The results demonstrate that FedNPG converges rapidly while the naïve baseline diverges, highlighting the importance of Q-tracking for stability and convergence.
Full paper#



















