↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current deep reinforcement learning methods achieve high performance in simulated robotic environments but require extensive computational resources and large datasets, making them unsuitable for real-world applications with limited resources. These methods struggle when limited to small replay buffers or during incremental learning. This paper highlights the issues of instability and high variance in incremental learning stemming from large and noisy gradients and proposes a new method to address those challenges.
The paper introduces a novel incremental deep policy gradient method called Action Value Gradient (AVG) along with normalization and scaling techniques to address these issues. AVG is shown to be significantly more effective than existing incremental methods and achieves comparable performance to batch methods on robotic simulation benchmarks. Moreover, the researchers demonstrate, for the first time, the effectiveness of deep reinforcement learning with real robots using only incremental updates, showcasing the advancement of the field and its potential for real-world applications.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in robotics and reinforcement learning. It addresses the critical need for real-time learning in resource-constrained environments, a major limitation of current deep RL methods. By introducing AVG, it opens new avenues for deploying deep RL on real-world robots and for developing more efficient and stable algorithms. Its impact extends to fields beyond robotics, as the approach is applicable to incremental learning problems in other domains.
Visual Insights#
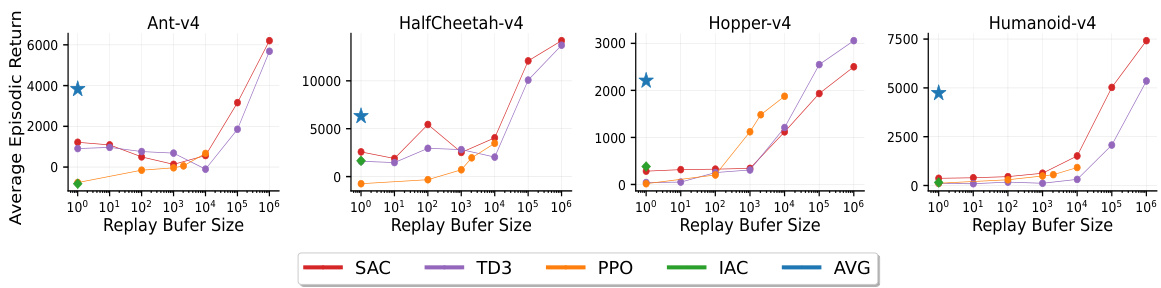
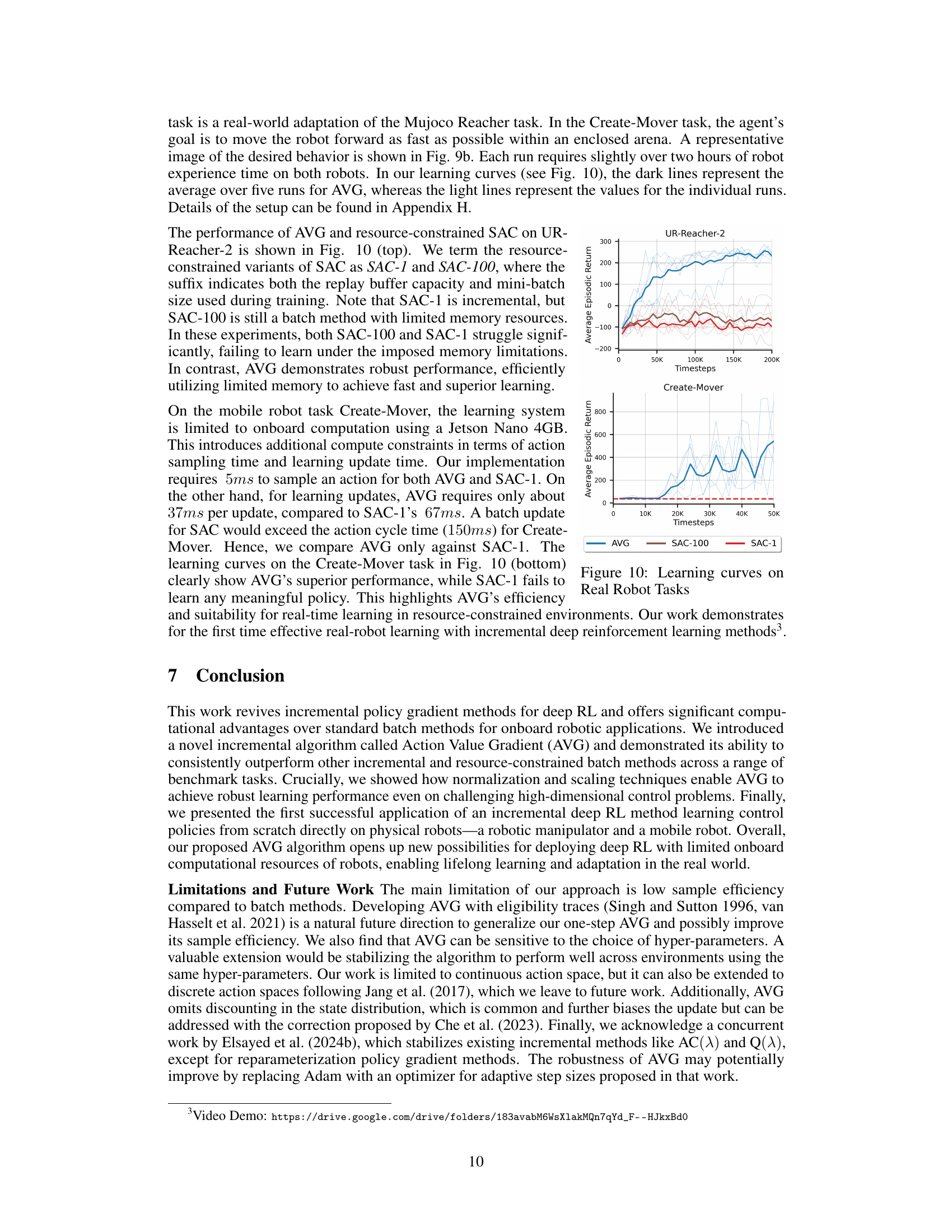
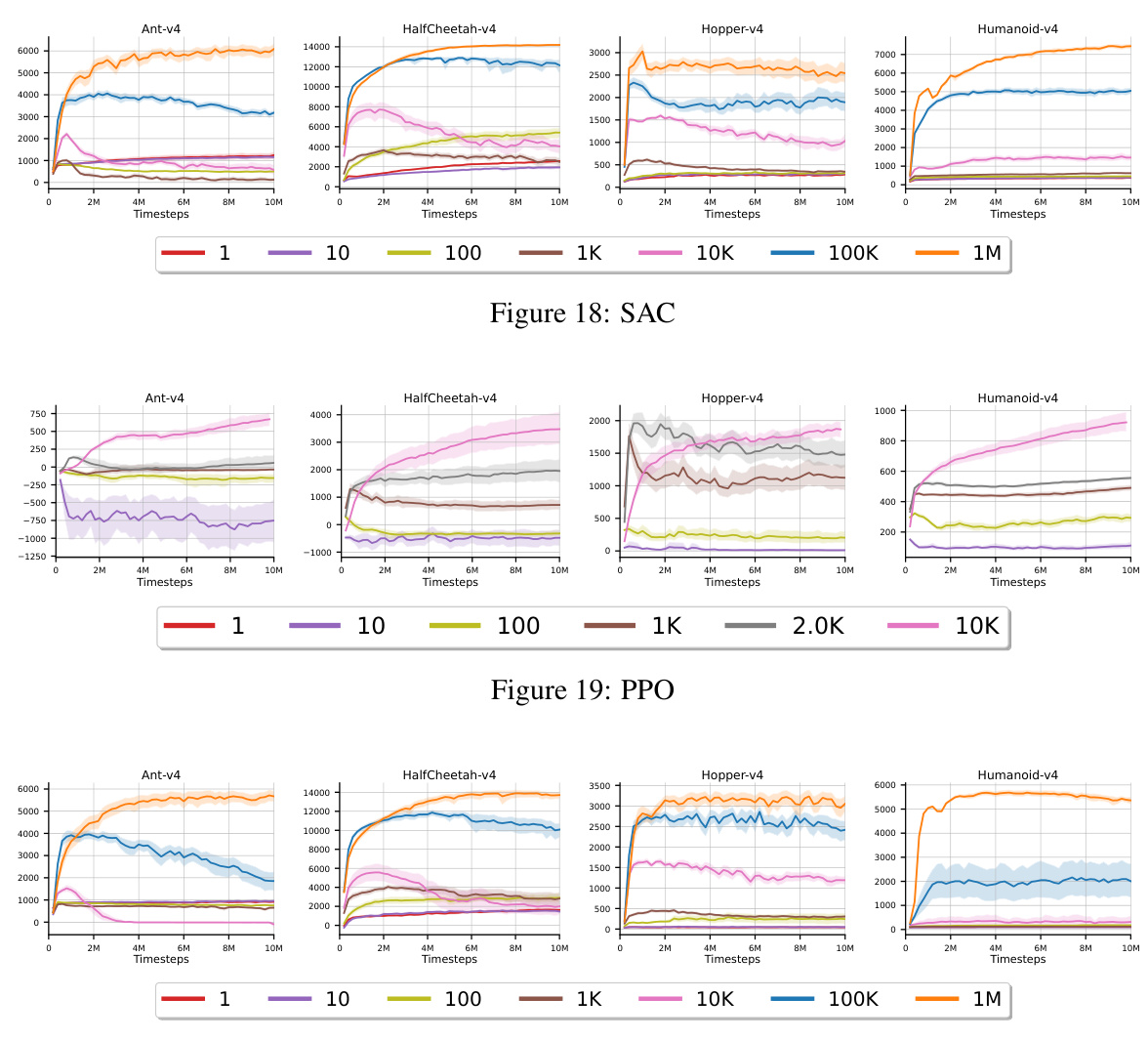
The figure shows the impact of reducing the replay buffer size on the performance of four reinforcement learning algorithms: SAC, TD3, PPO, and IAC. The x-axis represents the replay buffer size (log scale), and the y-axis represents the average episodic return over the last 100,000 timesteps of training, averaged across 30 independent runs. Each algorithm was trained for 10 million timesteps. The plot shows that the performance of SAC, TD3, and PPO degrades significantly as the replay buffer size decreases, demonstrating a strong dependency on experience replay for effective learning. In stark contrast, the proposed AVG algorithm maintains its performance even with a replay buffer size of 1 (essentially no replay buffer). This highlights AVG’s robustness and suitability for resource-constrained environments where large replay buffers are infeasible.

This table provides a comparison between the Soft Actor-Critic (SAC) algorithm and the Action Value Gradient (AVG) algorithm, highlighting key differences in their architecture, components, and learning mechanisms. It shows that SAC uses two Q-networks, two target Q-networks, a learned entropy coefficient, and a replay buffer, while AVG employs a simpler design with only one Q-network, no target network, a fixed entropy coefficient, and no replay buffer.
In-depth insights#
Incremental DRL#
Incremental Deep Reinforcement Learning (DRL) tackles the challenge of adapting DRL agents to dynamic environments with limited computational resources. Unlike batch DRL, which processes large datasets, incremental DRL updates the agent’s policy after each new experience, enabling real-time adaptation. This approach is particularly crucial for resource-constrained settings such as robots operating in the real world. While this reduces computational demands, incremental learning introduces instability due to noisy gradients and non-stationarity of the data stream. Therefore, effective incremental DRL methods require careful consideration of algorithmic design. This often involves incorporating normalization and scaling techniques to handle large and noisy updates, thereby enhancing stability and improving performance. The effectiveness of incremental DRL hinges on carefully balancing exploration and exploitation while managing computational constraints; finding a sweet spot between rapid adaptation and stable learning is essential. Successful incremental DRL methods can enable robust and adaptive behavior in resource-constrained agents operating in real-time.
AVG Algorithm#
The Action Value Gradient (AVG) algorithm stands out as a novel incremental deep policy gradient method designed for real-time reinforcement learning. Its core innovation lies in its ability to learn effectively without relying on batch updates, replay buffers, or target networks, all of which are computationally expensive and memory-intensive. This makes AVG particularly suitable for resource-constrained environments like robots and edge devices. The algorithm leverages the reparameterization gradient (RG) estimator for gradient calculation, addressing the instability issues often associated with incremental learning methods, primarily through normalization and scaling techniques. These techniques, specifically observation normalization, penultimate normalization, and TD error scaling, effectively mitigate issues stemming from large and noisy gradients. The AVG algorithm’s performance on various simulated benchmark tasks is significantly better than existing incremental methods, often achieving comparable results to batch methods. This advancement has led to its successful application on real robots, proving its capability for effective deep reinforcement learning in the real world. AVG’s unique blend of incremental updates, RG estimation, and stabilization techniques opens new possibilities for on-device learning in robotics and other resource-limited domains.
Real-Robot Tests#
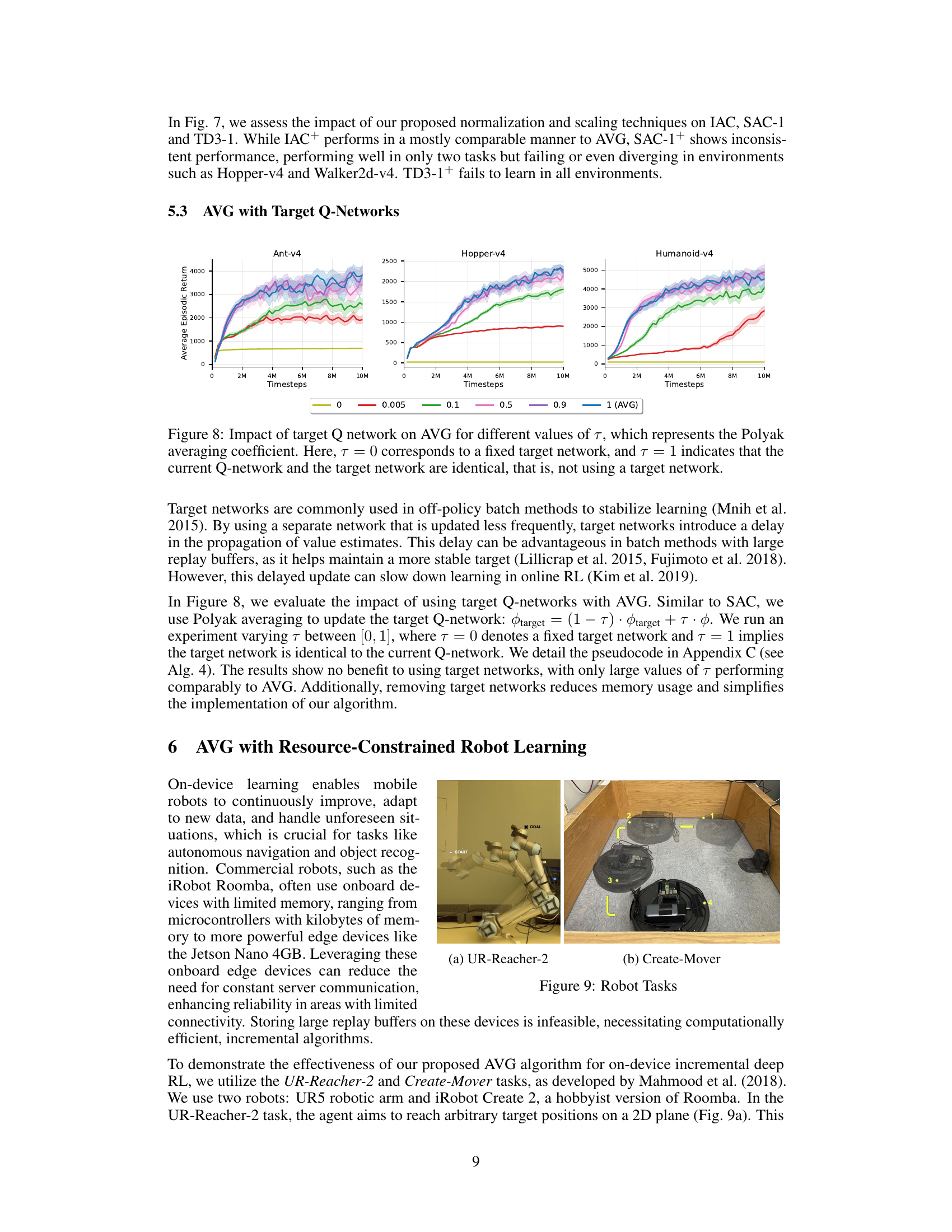
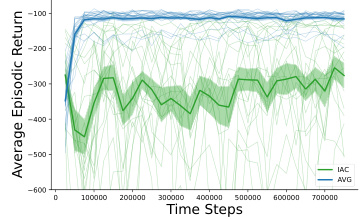
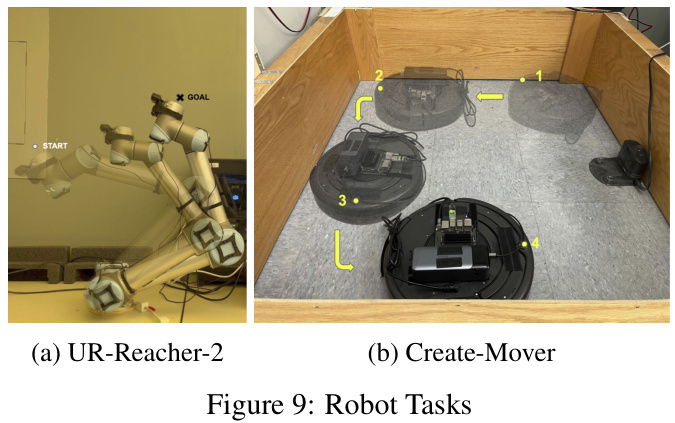
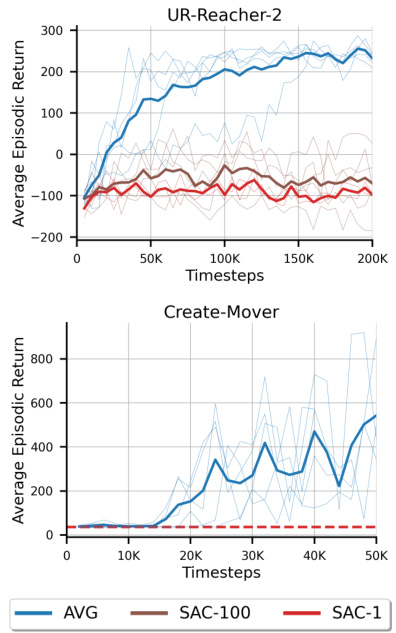
The ‘Real-Robot Tests’ section is crucial for evaluating the practical applicability of the proposed Action Value Gradient (AVG) algorithm. It bridges the gap between simulated and real-world performance, a common pitfall in reinforcement learning research. Successfully deploying AVG on real robots demonstrates its robustness and efficiency in resource-constrained environments. The choice of robotic platforms (a UR5 manipulator and an iRobot Create 2) is important; they represent different levels of computational power and control complexity, showcasing AVG’s adaptability. The reported results, including learning curves and performance metrics, should be meticulously analyzed to assess the algorithm’s effectiveness in these real-world settings, particularly noting its performance relative to established methods. The experimental setup description should be comprehensive enough to allow for reproducibility. A discussion of challenges encountered during real-robot implementation, such as noise, sensor limitations, and actuator dynamics, would add significant value and further underscore the practical significance of this work. Ultimately, the success or failure of the real-robot experiments is a key determinant of the paper’s overall impact and contribution to the field.
Normalization/Scaling#
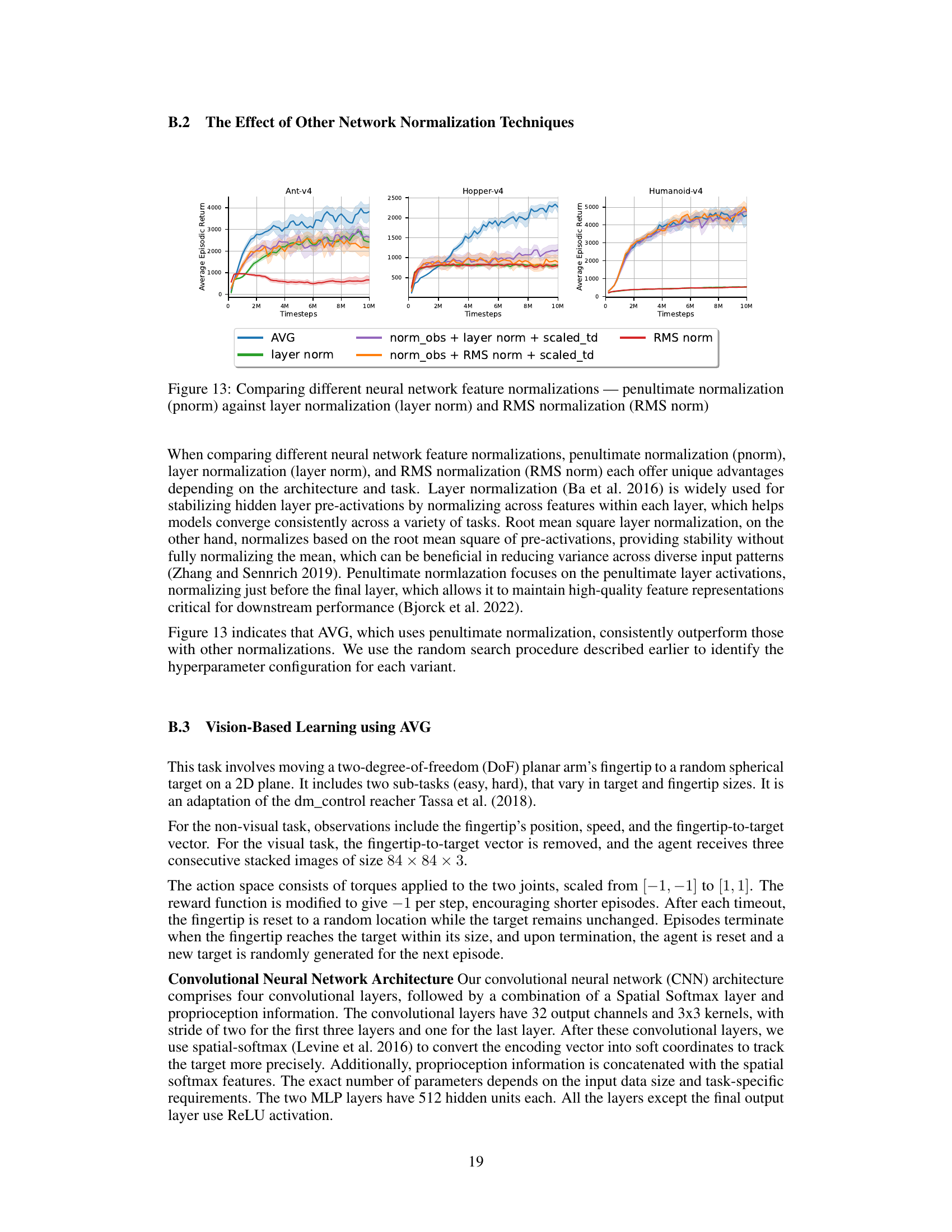
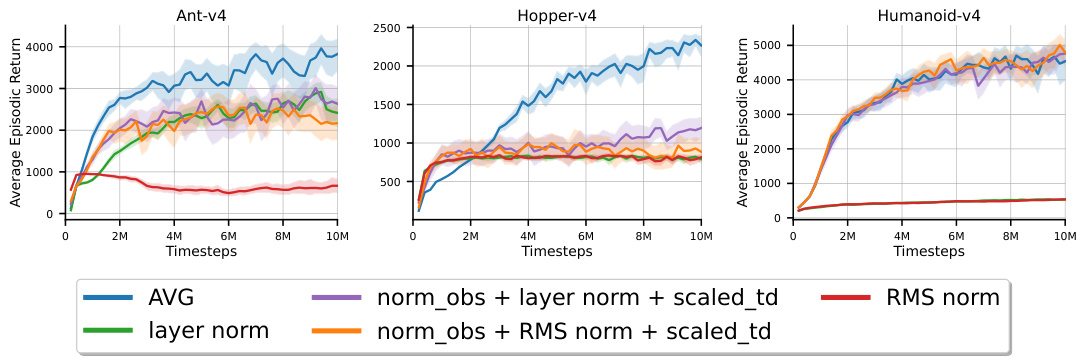
The research paper significantly emphasizes normalization and scaling techniques to stabilize the learning process in incremental deep reinforcement learning. The authors highlight the challenges of instability stemming from large and noisy gradients inherent in incremental settings, which can lead to catastrophic failure. They demonstrate that observation normalization, penultimate normalization, and TD error scaling are crucial for mitigating these issues, significantly improving learning stability and performance. The ablation study confirms the importance of these techniques, showcasing their effectiveness in helping the proposed algorithm (AVG) learn effectively, unlike other incremental methods. AVG successfully avoids catastrophic failures and demonstrates good learning performance even in challenging sparse reward environments. The choice of normalization and scaling strategies has a profound effect on performance in incremental deep RL, and these findings provide valuable insights for developing robust real-time learning systems.
Future Works#
The paper’s ‘Future Works’ section could fruitfully explore several avenues. Improving sample efficiency is paramount; the current method lags behind batch approaches. Investigating eligibility traces or other memory-based mechanisms could significantly enhance learning speed and reduce the data demands. Extending the algorithm to handle discrete action spaces would broaden its applicability to a wider range of robotics tasks. Addressing the sensitivity to hyperparameter choices is crucial for practical implementation; more robust optimization strategies or self-tuning mechanisms should be considered. Finally, a rigorous theoretical analysis of convergence under more realistic conditions (non-i.i.d. data, non-stationary environments) would significantly strengthen the paper’s foundation and provide more confident guarantees for real-world applications. Addressing these points would enhance the algorithm’s practical utility and solidify its position in the field of online deep reinforcement learning.
More visual insights#
More on figures
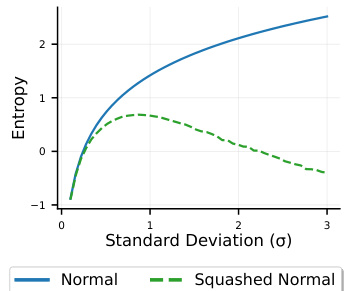
The figure shows the relationship between the standard deviation (σ) and entropy for both normal and squashed normal distributions. It illustrates that for a normal distribution, entropy increases monotonically with σ. However, for a squashed normal distribution, entropy initially increases with σ, reaches a maximum, and then decreases. This highlights the impact of using a squashed normal distribution, which is commonly used in reinforcement learning to ensure the actions remain within a bounded range, on the entropy of the policy.
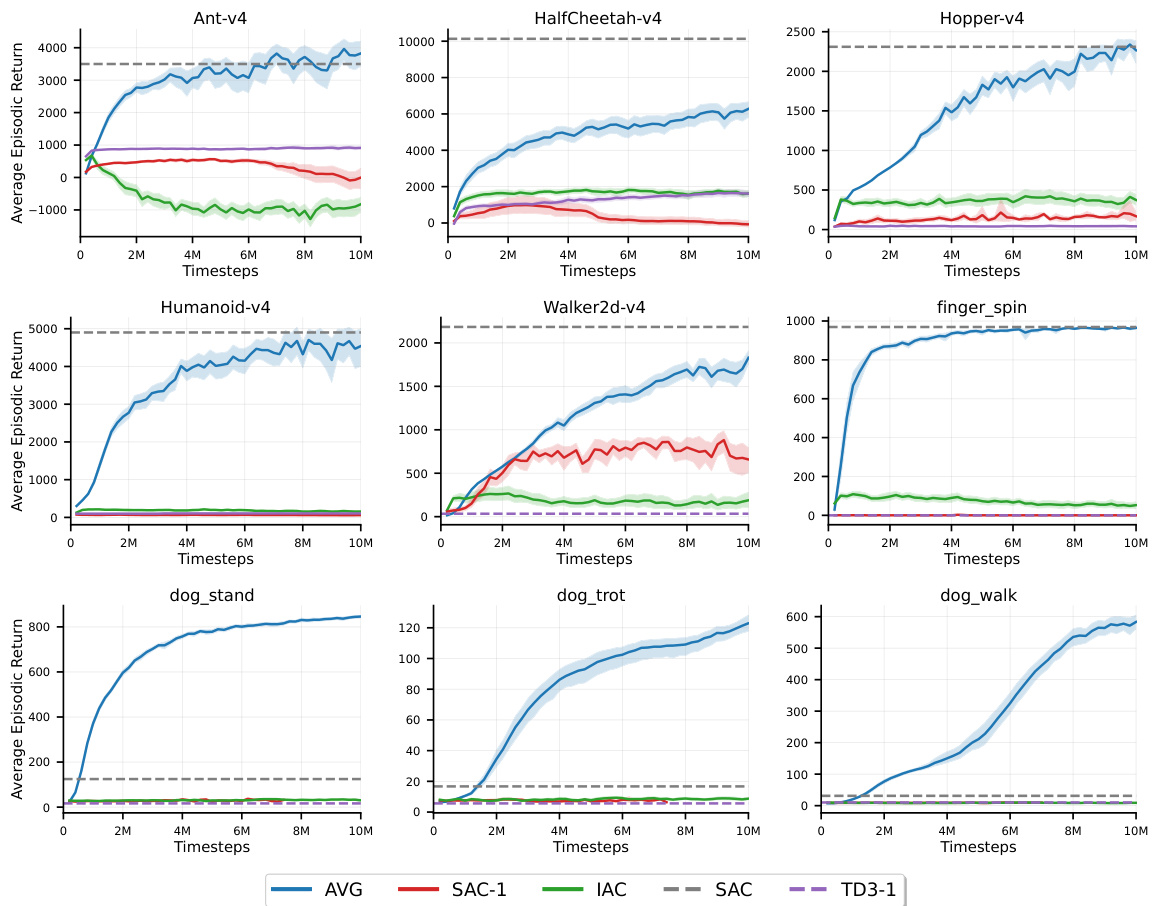
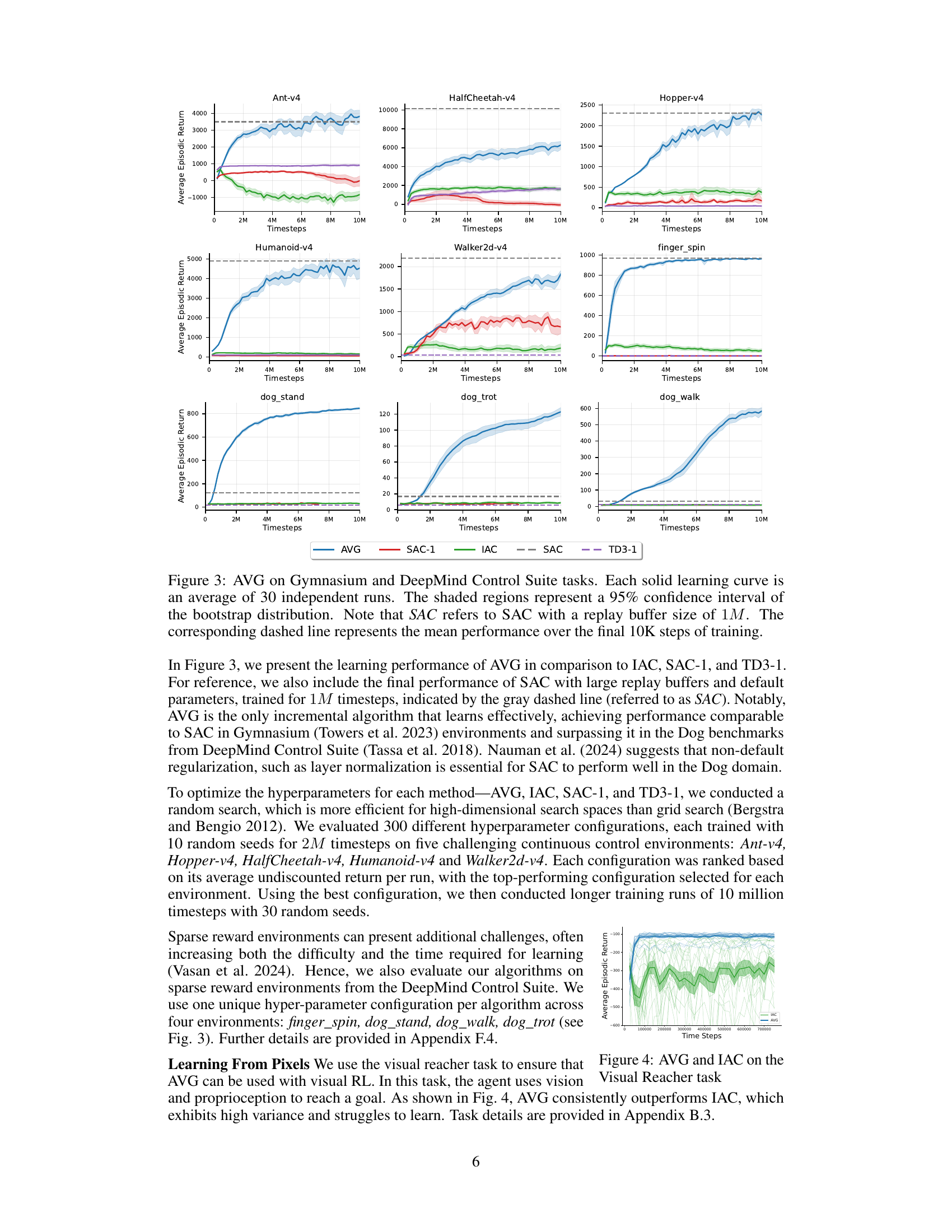
This figure compares the performance of AVG against three other incremental algorithms (IAC, SAC-1, and TD3-1) across various benchmark tasks. It also includes the performance of the standard SAC algorithm with a large replay buffer (1M samples) for comparison. The results show that AVG is the only incremental algorithm that consistently learns effectively, frequently achieving comparable or superior final performance to the non-incremental SAC.
This figure compares the performance of the proposed Action Value Gradient (AVG) algorithm to three other incremental algorithms (IAC, SAC-1, TD3-1) and one batch algorithm (SAC) across eight continuous control tasks. AVG consistently outperforms the other incremental algorithms and achieves comparable performance to the batch algorithm (SAC) which utilizes a much larger replay buffer. The shaded areas represent the 95% confidence interval for each learning curve showing the average episodic return over 10 million timesteps.
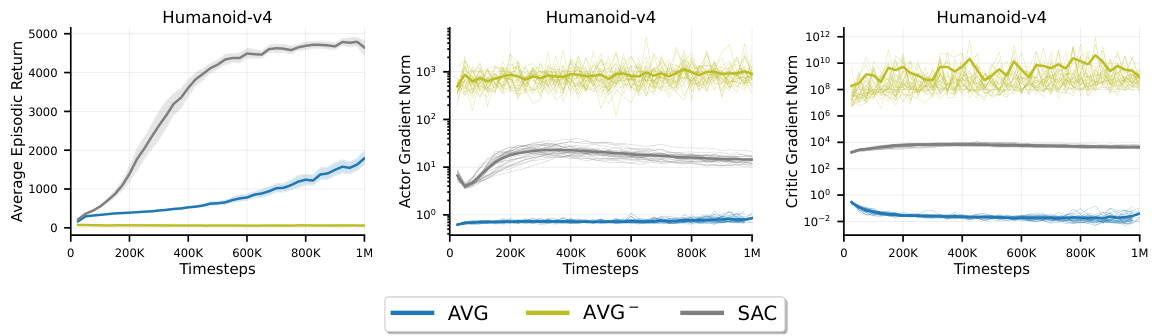
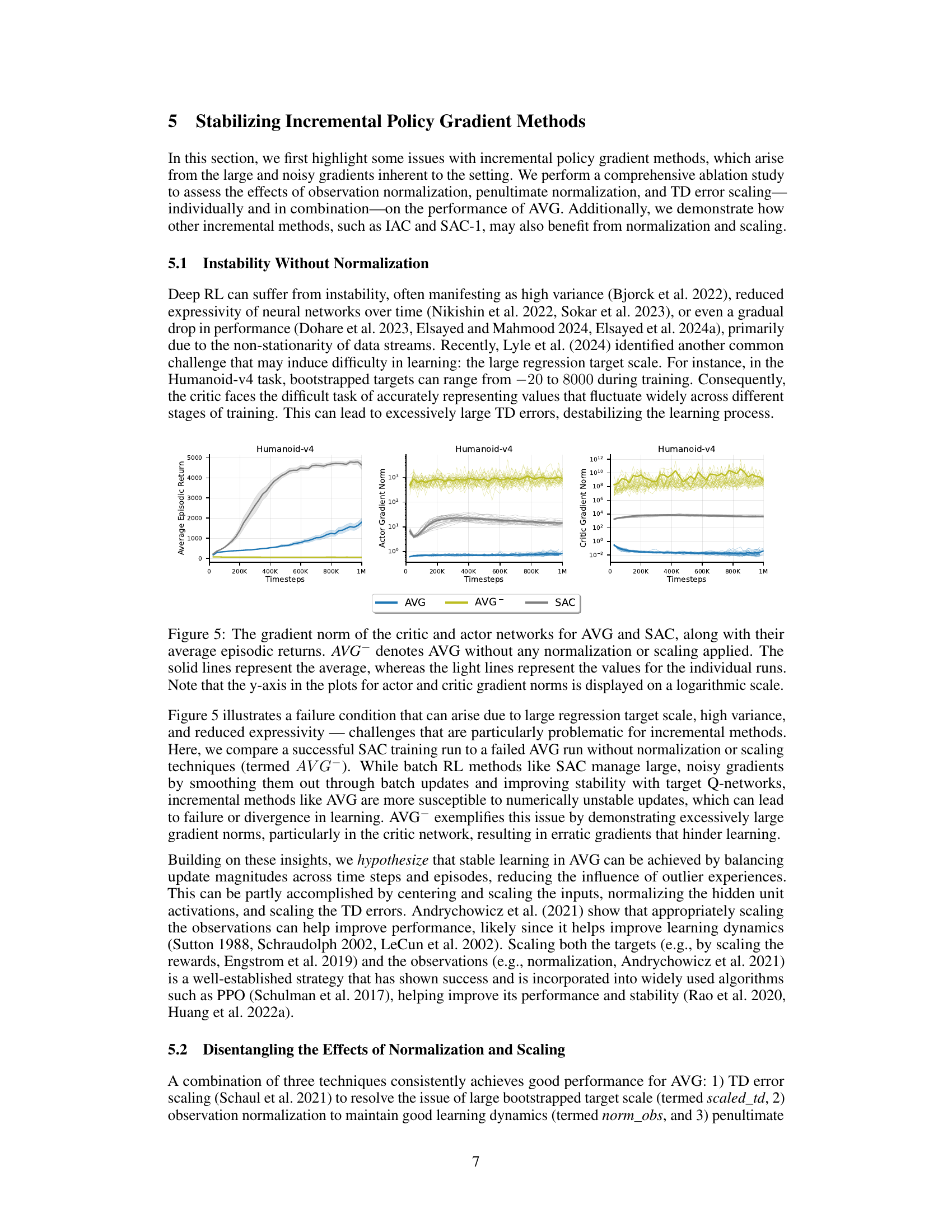
This figure compares the gradient norms of the actor and critic networks for AVG and SAC, along with their average episodic returns. The results show that AVG without normalization and scaling (AVG¯) suffers from instability, manifesting as high variance in the gradients. In contrast, SAC demonstrates stable learning with smoothly decreasing gradient norms.

This figure compares the performance of the proposed Action Value Gradient (AVG) method against other incremental and batch methods across various continuous control tasks from the Gymnasium and DeepMind Control Suite. It visually demonstrates AVG’s learning curves (average of 30 runs with 95% confidence intervals) and contrasts them with those of IAC, SAC-1, and TD3-1 (all incremental methods) along with the performance of SAC (batch method with a large replay buffer). The dashed lines show the mean performance over the final 10,000 steps.
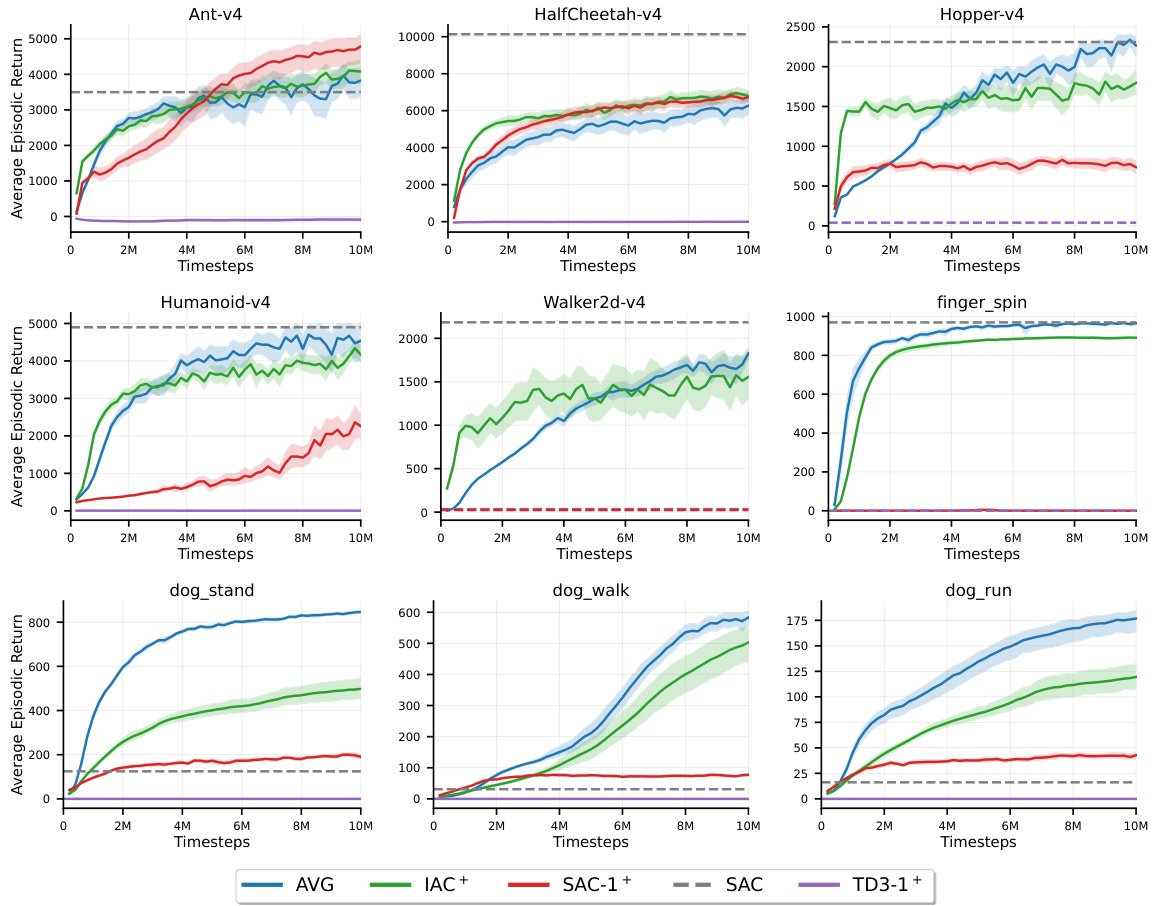
This figure compares the performance of the proposed Action Value Gradient (AVG) method to several other incremental and batch methods across a range of continuous control tasks from the Gymnasium and DeepMind Control Suite benchmark environments. The solid lines show the average episodic return over 30 independent runs for each method, with shaded regions indicating the 95% confidence intervals. The dashed lines represent the mean performance at the end of training. The figure highlights AVG’s superior performance compared to other incremental methods and its ability to compete with batch methods even with a greatly reduced replay buffer size.
This figure compares the performance of the proposed Action Value Gradient (AVG) algorithm against three other incremental algorithms (IAC, SAC-1, TD3-1) and a standard batch algorithm (SAC) across eight different continuous control tasks. The results illustrate AVG’s superior performance and ability to learn effectively in an incremental setting, often matching or exceeding the performance of batch methods that use replay buffers and target networks.
The figure shows the learning curves of AVG, IAC, SAC-1, and TD3-1 across multiple continuous control tasks in the Gymnasium and DeepMind Control Suite environments. The solid lines represent the average episodic returns over 30 independent runs, while shaded areas represent 95% confidence intervals. For comparison, the performance of SAC with a large replay buffer (1M) is also included (grey dashed line). The results demonstrate that AVG is the only incremental algorithm that learns effectively, often achieving a final performance comparable to, or better than, the batch method.
This figure compares the performance of AVG against three other algorithms (IAC, SAC-1, TD3-1) across multiple continuous control tasks from the Gymnasium and DeepMind Control Suite benchmark environments. It shows that AVG is the only incremental algorithm that successfully learns across these different tasks, and that its performance is comparable to or even surpasses that of batch RL methods (SAC) that have access to much larger replay buffers.
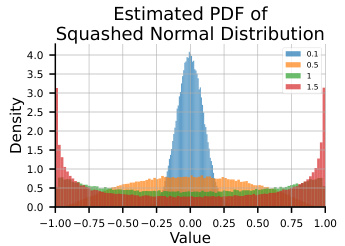
The figure shows the probability density function (PDF) of a squashed normal distribution. A squashed normal distribution is used in the paper because it provides bounded actions in the range [-1, 1], which is suitable for many reinforcement learning tasks. The plot displays how the entropy of the distribution changes with the standard deviation (σ). For small σ, the distribution is close to a delta function, so entropy is low. As σ increases, entropy increases, but once σ reaches a certain threshold, entropy begins to decrease again. This is because values become increasingly likely to be close to the boundaries of the [-1,1] interval. The effect of this is illustrated in the paper, because it helps prevent issues stemming from algorithms that continuously maximize entropy driving o to large values, thus approximating a uniform random policy.
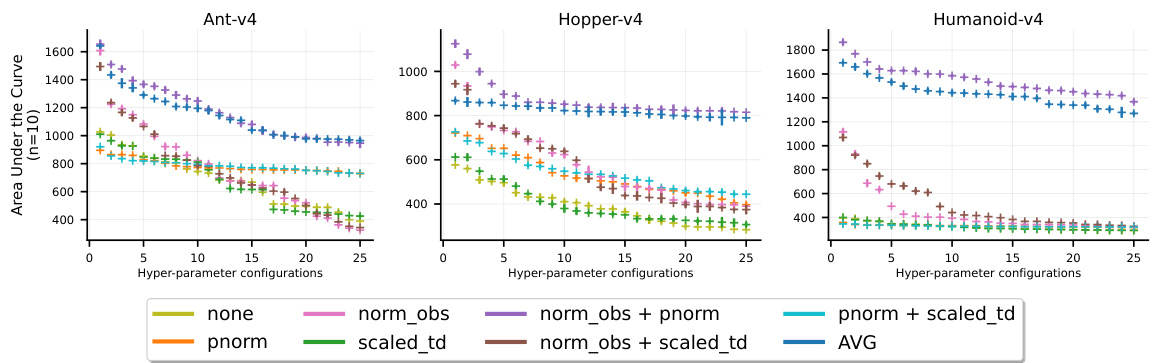
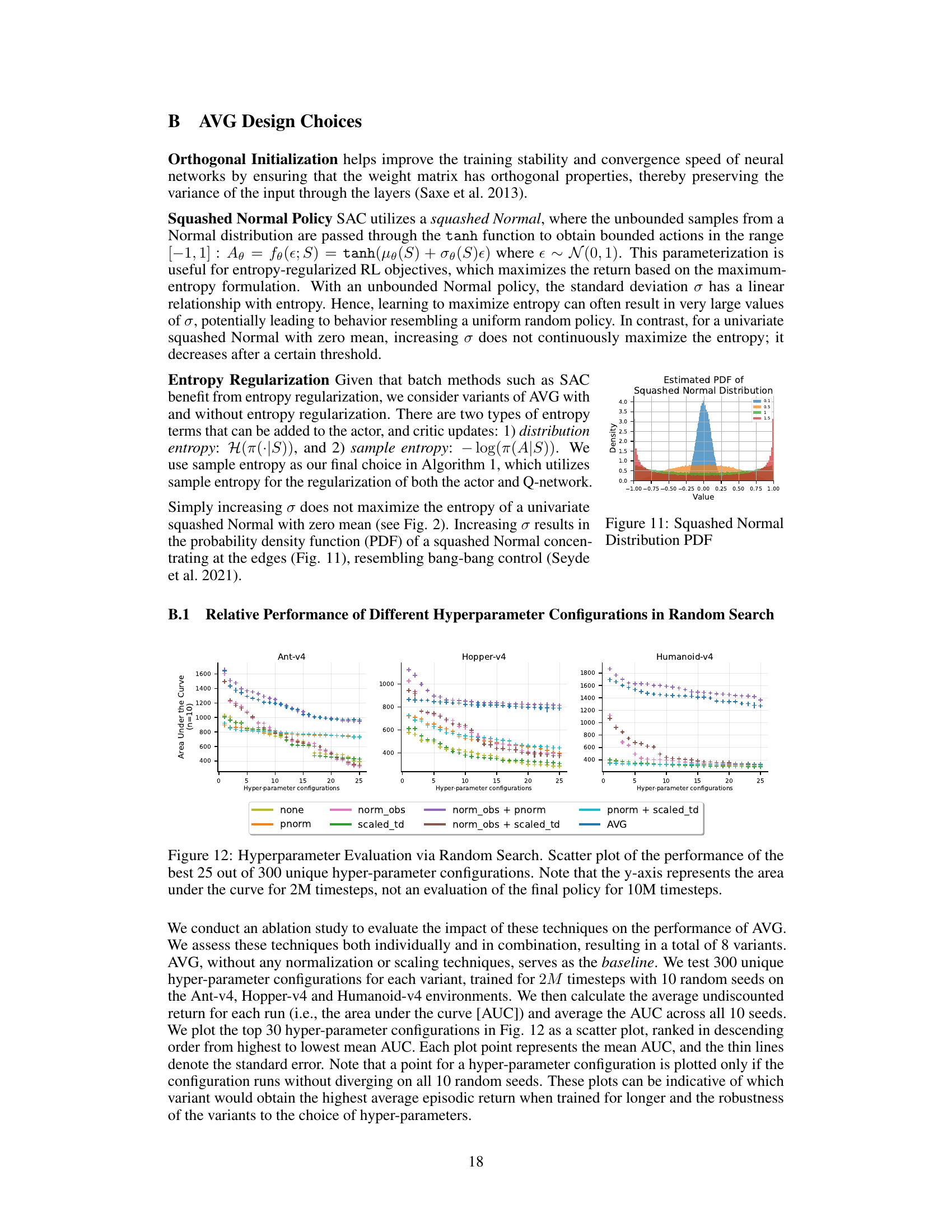
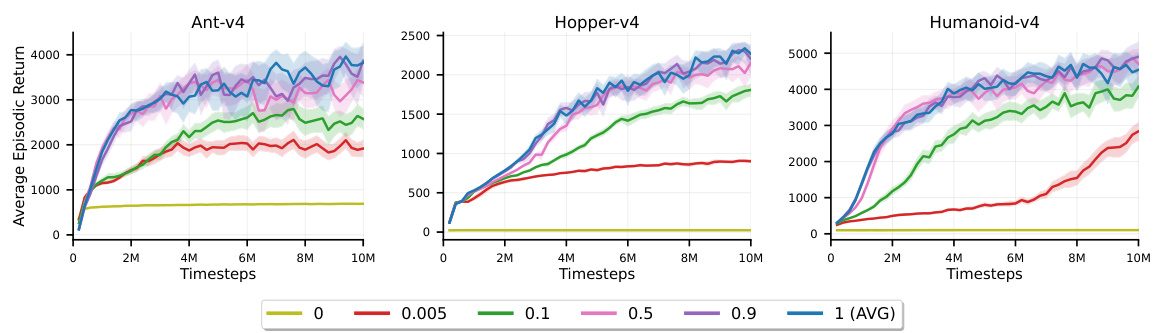
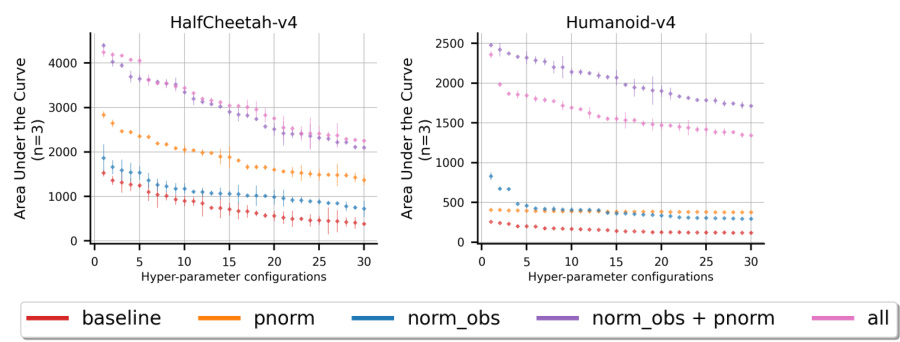
This figure shows the result of a hyperparameter search for the AVG algorithm. It displays a scatter plot comparing the area under the curve (AUC) of 25 of the best hyperparameter configurations (out of 300 tested) across three different MuJoCo environments. The AUC is calculated for the first 2 million timesteps of training. The plot helps to visualize the relative performance of different hyperparameter configurations, aiding in selecting the best set for AVG. Each data point represents the mean AUC across 10 random seeds, and the error bars illustrate standard deviation.
This figure compares the performance of the proposed Action Value Gradient (AVG) method against other incremental methods (IAC, SAC-1, TD3-1) and a batch method (SAC) across multiple continuous control tasks from the Gymnasium and DeepMind Control Suite environments. The results show that AVG is the only incremental method that learns effectively, often achieving final performance comparable to batch methods. The shaded areas represent 95% confidence intervals, indicating the variability across multiple runs.
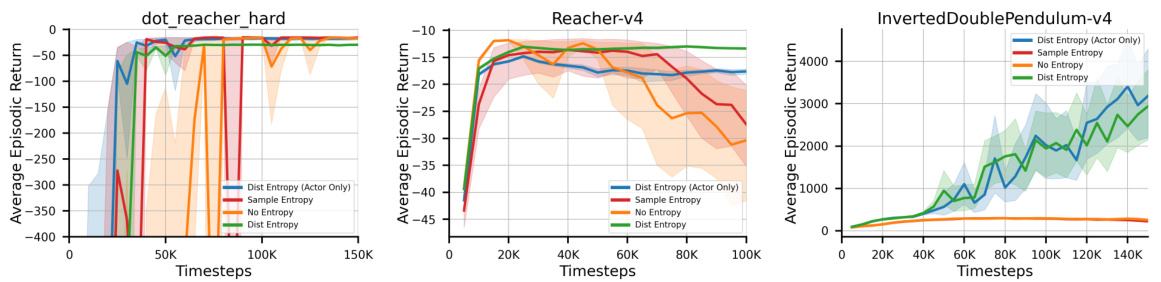
The figure presents the learning curves of the Incremental Actor Critic (IAC) algorithm across three different MuJoCo continuous control tasks: dot_reacher_hard, Reacher-v4, and InvertedDoublePendulum-v4. Four variants of the algorithm are compared: one with no entropy regularization, one using distribution entropy only in the actor, one using sample entropy, and one using both distribution and sample entropy. The plots show the average episodic return over the course of training, with shaded regions illustrating 95% confidence intervals. The results demonstrate how different entropy regularization approaches affect learning performance in these benchmark tasks, highlighting the role of entropy in stabilizing and improving the learning process of this incremental RL method.

The figure displays the learning curves for different variants of the Incremental Actor Critic (IAC) algorithm across four MuJoCo environments (Ant-v4, HalfCheetah-v4, Hopper-v4, Inverted Double Pendulum-v4). Each line represents a different entropy configuration (Sample Entropy, No Entropy, Dist Entropy (Actor Only), and Dist Entropy). The shaded areas represent 95% confidence intervals. The results highlight the impact of entropy regularization on the performance of IAC, comparing distribution entropy and sample entropy and illustrating the variability inherent in incremental learning.
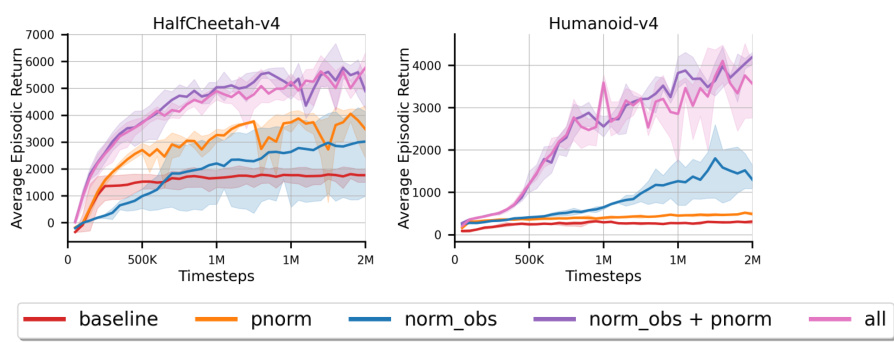
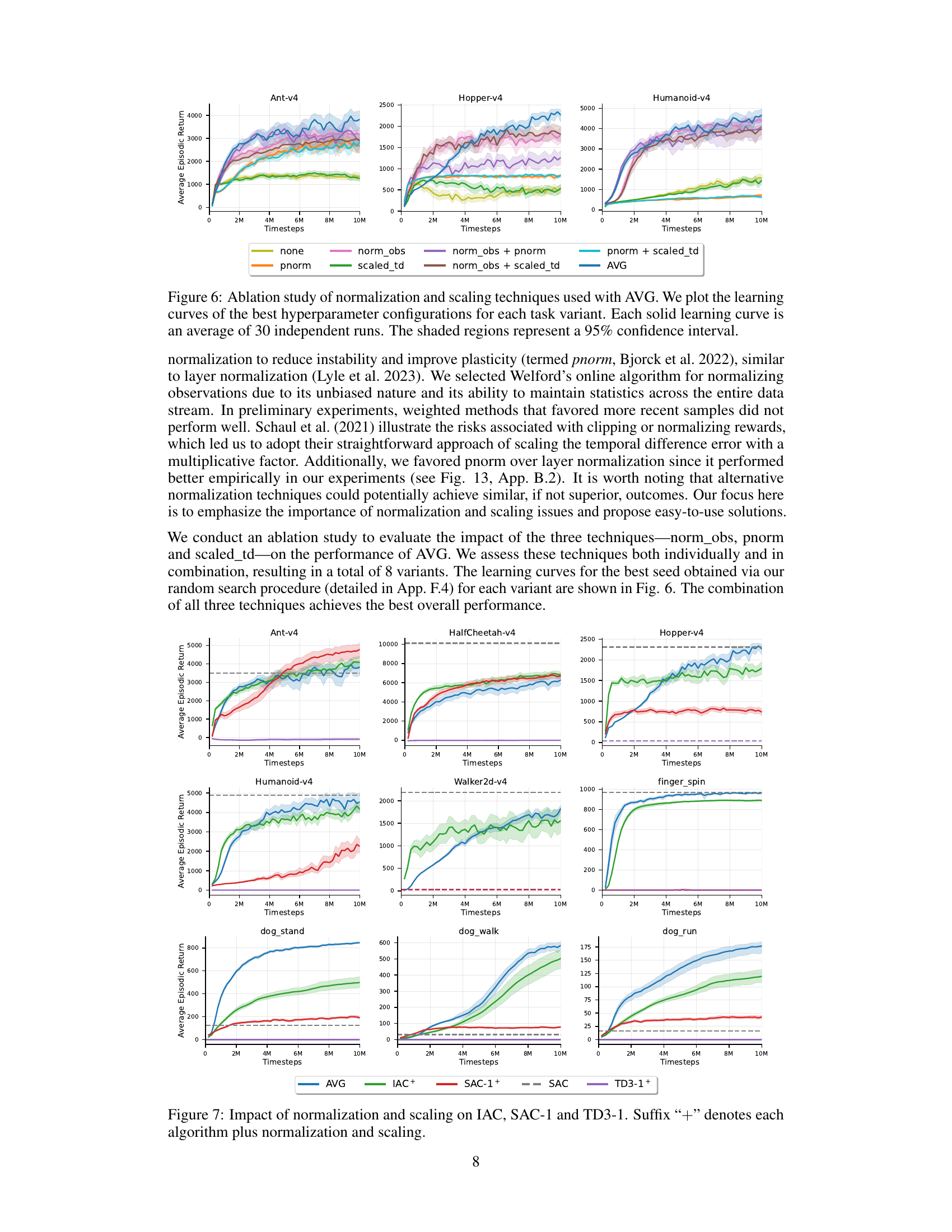
This figure shows the ablation study of normalization and scaling techniques used with the AVG algorithm. Different variants of AVG are compared: a baseline without any normalization/scaling, variants with observation normalization, penultimate normalization, scaled temporal difference errors, and combinations of these. The learning curves show the average episodic return over 30 independent runs for each variant, illustrating the impact of each technique on learning performance. The shaded regions represent the 95% confidence intervals.
This figure shows the ablation study on the effect of normalization and scaling techniques in AVG. The learning curves for eight different AVG variants are plotted, each representing a combination of observation normalization, penultimate normalization, and TD error scaling. The best hyperparameter configuration for each variant was used. The results demonstrate that combining all three techniques leads to the best overall performance.
This figure compares the performance of the proposed Action Value Gradient (AVG) algorithm with other incremental and batch deep reinforcement learning algorithms on various continuous control tasks from the Gymnasium and DeepMind Control Suite. It showcases AVG’s ability to learn effectively in an incremental setting (without a replay buffer), often achieving performance comparable to batch methods which require significantly more resources.

This figure compares the performance of the proposed Action Value Gradient (AVG) method against other incremental methods (IAC, SAC-1, TD3-1) and a batch method (SAC) on various continuous control tasks from the Gymnasium and DeepMind Control Suite. AVG consistently shows superior performance, often matching or exceeding that of the batch method, even with a much smaller replay buffer (or none at all). The shaded areas represent confidence intervals, showing the consistency of AVG’s results.
More on tables

This table provides a concise comparison of the Soft Actor-Critic (SAC) and Action Value Gradient (AVG) algorithms, highlighting key architectural differences and design choices. It shows that SAC uses two Q-networks, two target Q-networks, a learned entropy coefficient, and a replay buffer, while AVG utilizes a single Q-network, no target networks, a fixed entropy coefficient, and no replay buffer. These differences reflect the core distinction between the off-policy batch approach of SAC and the on-policy incremental nature of AVG.
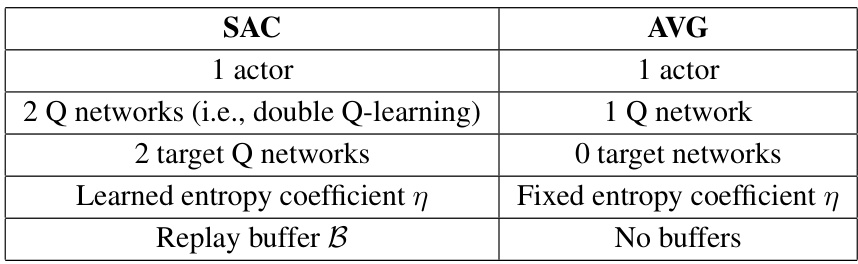
This table summarizes the key differences between the Soft Actor-Critic (SAC) algorithm and the proposed Action Value Gradient (AVG) algorithm. It highlights that SAC uses two Q-networks, two target Q-networks, a learned entropy coefficient, and a replay buffer, while AVG uses a single Q-network, no target networks, a fixed entropy coefficient, and no replay buffer. The differences reflect AVG’s design goal of being a simpler, more resource-efficient incremental algorithm compared to the off-policy SAC.
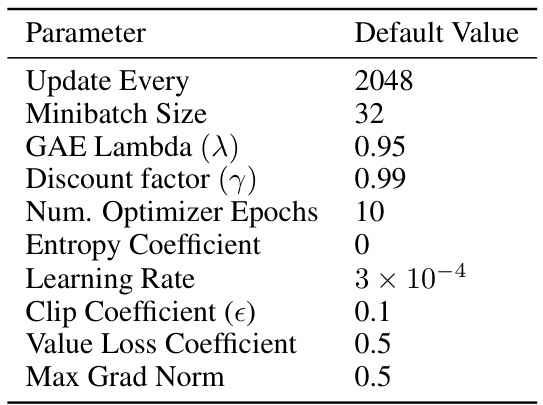
This table lists the hyperparameters used in the Proximal Policy Optimization (PPO) algorithm implementation from the CleanRL library. It includes values for parameters such as update frequency, minibatch size, generalized advantage estimation (GAE) lambda, discount factor, number of optimizer epochs, entropy coefficient, learning rate, clip coefficient, value loss coefficient, and maximum gradient norm. These settings are crucial for controlling the learning process and balancing exploration-exploitation trade-offs in the reinforcement learning task.
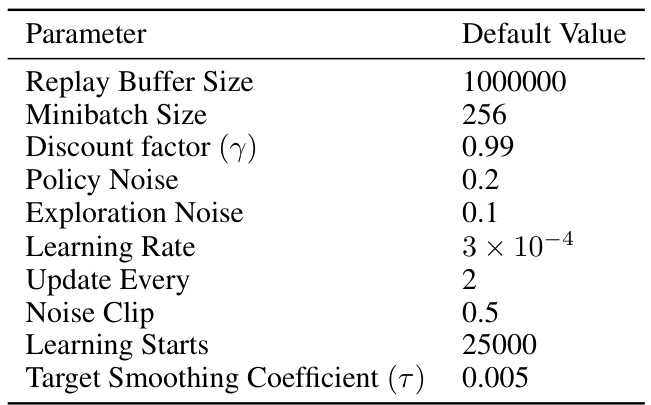
This table lists the default hyperparameters used in the CleanRL implementation of the Twin Delayed Deep Deterministic Policy Gradient (TD3) algorithm. These parameters control aspects of the replay buffer, minibatch size, discount factor, exploration and policy noise, learning rate, update frequency, noise clipping, when learning starts, and target smoothing coefficient.
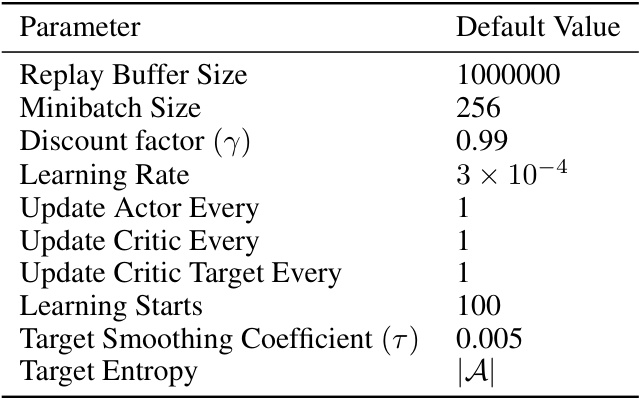
This table lists the default hyperparameters used in the CleanRL implementation of the Twin Delayed Deep Deterministic policy gradient (TD3) algorithm. These parameters control various aspects of the training process, including the size of the replay buffer, the minibatch size used for updates, the discount factor, exploration and policy noise parameters, learning rate, update frequency, target network update parameters, and more. The settings shown are the defaults provided by the CleanRL library, and may have been adjusted during experimentation as described in the paper.
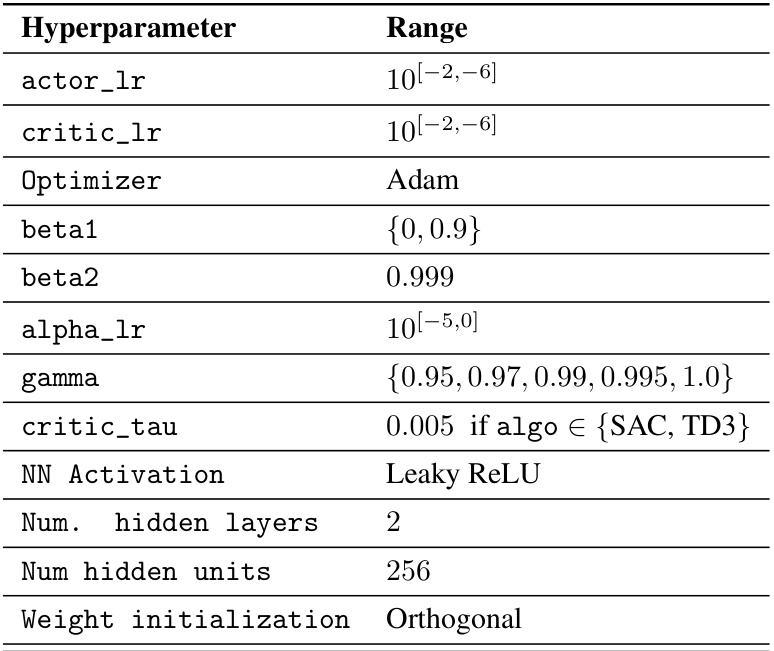
This table details the hyperparameter ranges used in a random search for optimizing the actor and critic learning rates, Adam optimizer parameters (beta1, beta2), entropy coefficient (alpha_lr), discount factor (gamma), and Polyak averaging coefficient (critic_tau). The neural network activation function (Leaky ReLU), number of hidden layers (2), number of hidden units (256), and weight initialization method (Orthogonal) are also specified.
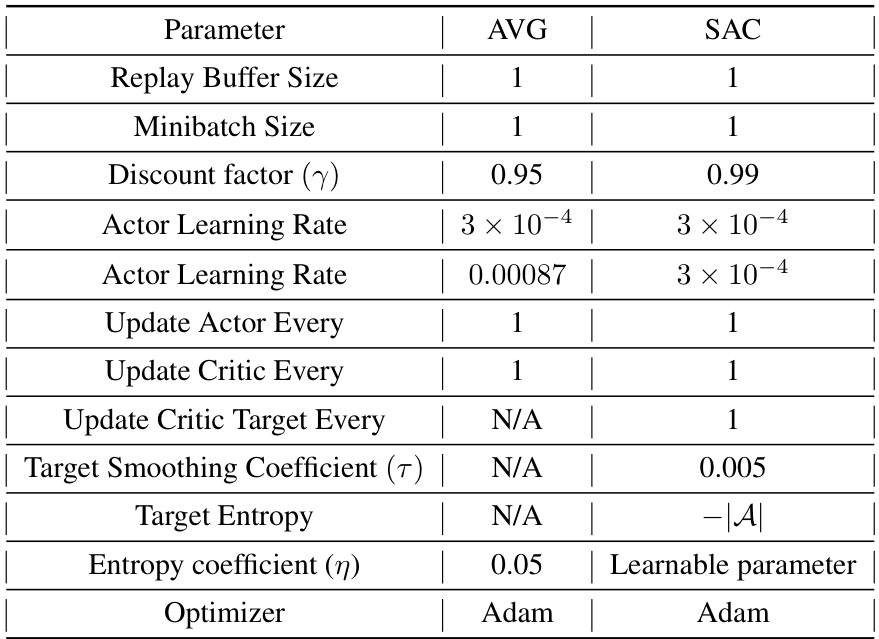
This table lists the hyperparameters used for both the AVG and SAC algorithms when applied to real robot experiments. It shows the differences in parameters such as replay buffer size (which is 1 for AVG, indicating no replay buffer), minibatch size, discount factor, learning rates for actor and critic networks, update frequencies for actor and critic networks, target smoothing coefficients (only used for SAC), target entropy, entropy coefficients and the optimizer used. The table highlights the key differences in the approach taken for incremental learning in AVG versus the batch methods in SAC, especially in the management of replay buffers and target networks.

This table provides a comparison between the Soft Actor-Critic (SAC) algorithm and the proposed Action Value Gradient (AVG) algorithm. It highlights key differences in the number of networks, the use of target networks, the presence of a replay buffer, and the treatment of the entropy coefficient. The comparison emphasizes the differences in architecture and training methods between the off-policy SAC and the on-policy AVG algorithms.
Full paper#