TL;DR#
Dueling bandits, a type of online learning problem, involve sequentially selecting pairs of options and learning from user preferences expressed as pairwise comparisons. Minimizing regret (the difference in cumulative reward between the optimal strategy and the learner’s strategy) is a key goal. Existing research mostly focuses on strong regret, where the learner only avoids loss by consistently choosing the optimal option twice. However, many real-world scenarios, like recommendation systems, only require one optimal choice to succeed, motivating research into weak regret minimization.
This paper addresses the challenges of weak regret minimization in stochastic dueling bandits, assuming only the existence of a Condorcet winner (an option superior to all others). The authors propose two novel algorithms, WR-TINF and WR-EXP3-IX, which adaptively balance exploration and exploitation based on the problem’s specific structure (the pairwise preference probabilities). They prove that WR-TINF achieves optimal regret in certain regimes, while WR-EXP3-IX outperforms it in others, showcasing a more nuanced and challenging aspect of dueling bandit problems compared to the traditional strong regret.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in online learning and decision-making. It tackles the challenging problem of weak regret minimization in dueling bandits, offering novel algorithms and theoretical bounds. The findings directly impact applications like recommender systems and online advertising, where optimizing user engagement is paramount. The work also opens new research directions in characterizing optimal regret in dueling bandit problems with nuanced gap structures, moving beyond traditional strong regret analysis. This could lead to more efficient and effective algorithms with improved performance guarantees, benefiting numerous applications.
Visual Insights#
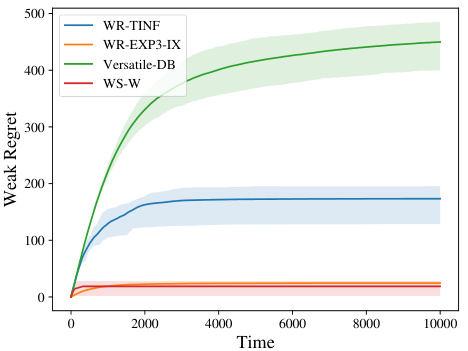
🔼 The figure shows the performance of four different algorithms for dueling bandits in three different scenarios. Scenario 1 (small problem) demonstrates weak regret with a small number of arms where the Strong Stochastic Transitivity (SST) condition holds. Scenario 2 (moderate problem) shows both weak and strong regret with moderately sized problems and no SST. Scenario 3 (large problem) demonstrates weak regret with many arms and no SST. The algorithms compared are WR-TINF, WR-EXP3-IX, Versatile-DB, and WS-W. The plots include mean regret values along with shaded areas representing 0.2 and 0.8 quantiles, illustrating variability across different experimental runs.
read the caption
Figure 1: Performance of algorithms in different scenarios

🔼 This table summarizes the performance of different algorithms (WR-TINF, WR-EXP3-IX, Versatile-DB, and WS-W) for minimizing weak regret in three different scenarios of dueling bandits. Scenario 1 involves a small number of arms and satisfies the strong stochastic transitivity (SST) assumption. Scenario 2 involves a moderate number of arms and does not satisfy SST. Scenario 3 involves a large number of arms and does not satisfy SST. For each scenario and algorithm, the table reports the average weak regret over 20 iterations, along with 0.2 and 0.8 quantiles to illustrate the variability of the results.
read the caption
Table 1: Weak regret of different algorithms for dueling bandits in different scenarios
In-depth insights#
Weak Regret’s Nature#
Analyzing “Weak Regret’s Nature” within the context of dueling bandits reveals a nuanced landscape. Unlike strong regret, which penalizes the learner for not selecting the Condorcet winner twice, weak regret focuses on situations where only one selection is sufficient. This makes weak regret minimization particularly relevant in applications like online advertising or recommendation systems, where single positive interactions are crucial. The key challenge lies in the inherent nonlinearity of the weak regret definition, which complicates theoretical analysis. Existing literature reveals that optimal regret is heavily dependent on the problem’s structure. This includes the optimality gap of the Condorcet winner and the relative gaps between suboptimal arms, which is a significant departure from strong regret analysis. This highlights the need for sophisticated algorithms that can dynamically balance exploration and exploitation based on this complex interplay of gaps. Finally, the absence of a total order over arms adds further complexity, requiring strategies that are robust to various dueling outcomes and adapt to the structure of the problem. The research on this topic emphasizes that the theoretical understanding of weak regret is not straightforward and differs drastically from the strong regret paradigm.
Dueling Bandit Bounds#
Analyzing dueling bandit bounds involves investigating the theoretical limits of performance for algorithms tackling this specific type of bandit problem. A key aspect is understanding the relationship between the regret (the difference between the algorithm’s performance and that of an optimal strategy) and various problem parameters, such as the number of arms (K), the time horizon (T), and the structure of the underlying preference matrix. The bounds themselves can be categorized into instance-dependent bounds, which tightly characterize regret for a given problem instance based on the structure of its pairwise preference probabilities, and instance-independent bounds, which provide worst-case guarantees across all problem instances. Tight instance-dependent bounds are particularly valuable as they reveal the inherent difficulty of specific problems, while instance-independent bounds serve as more general guarantees. Research in this area often focuses on deriving both upper and lower bounds: upper bounds demonstrate the performance that algorithms can achieve, while lower bounds establish fundamental limits. The gap between upper and lower bounds represents the remaining space for algorithm improvement. Furthermore, the analysis often considers different regret notions, such as strong regret (requiring both selected arms to be optimal to avoid loss) and weak regret (only one arm needs to be optimal). Weak regret is often more relevant in practical settings where only one correct choice is required for a successful outcome. Ultimately, a deep understanding of dueling bandit bounds is critical to designing efficient and optimal algorithms for a wide range of applications.
WR-TINF Algorithm#
The WR-TINF algorithm, a novel approach to weak regret minimization in dueling bandits, is presented. It cleverly adapts the Tsallis-INF regularizer within an online mirror descent framework. WR-TINF addresses the challenge of balancing exploration and exploitation by employing a nuanced sampling strategy, dynamically adjusting the exploration rate based on the observed preferences. This adaptive approach is particularly crucial in weak regret settings, where only one optimal choice is needed to avoid loss, unlike strong regret where two are needed. A key strength is its theoretical optimality under specific conditions, such as a non-negligible optimality gap, which is proven through rigorous analysis and characterized by a regret bound. The algorithm’s performance improves upon existing methods, demonstrating its effectiveness in scenarios with varying numbers of arms and diverse optimality gap structures. Its rigorous theoretical analysis and empirical results highlight the effectiveness and efficiency of the algorithm in achieving near-optimal weak regret, making it a valuable contribution to the field of dueling bandits.
WR-EXP3-IX Strategy#
The WR-EXP3-IX strategy, proposed as an alternative to WR-TINF, tackles the weak regret minimization problem in dueling bandits by leveraging the full structure of the pairwise preference matrix. Unlike WR-TINF which focuses primarily on duels involving the Condorcet winner, WR-EXP3-IX aims to efficiently eliminate suboptimal arms by strategically selecting duels between non-Condorcet winner arms. This approach is particularly beneficial when the gaps between suboptimal arms are larger than the gaps between suboptimal arms and the Condorcet winner. WR-EXP3-IX’s adaptive nature allows it to outperform WR-TINF in scenarios where direct targeting of the Condorcet winner is less efficient. The algorithm’s reliance on EXP3-IX for arm selection makes it computationally more intensive, yet it potentially achieves superior regret bounds in specific problem structures. However, the optimality and overall performance depend heavily on the specific characteristics of the pairwise preference matrix, highlighting the complexity of the weak regret minimization problem.
Future Research#
Future research directions stemming from this work on weak regret in dueling bandits could explore several promising avenues. Relaxing the Condorcet winner assumption and investigating scenarios with more complex preference structures, such as cyclical relationships between arms, would be valuable. Developing algorithms that adaptively balance exploration and exploitation based on the observed gap matrix structure is crucial; current approaches are effective in specific regimes but not universally optimal. Further theoretical work should focus on sharpening lower bounds for weak regret to better understand the fundamental limits of learning in this setting. Finally, extending the analysis to non-stochastic environments, such as adversarial or bandit feedback models, presents a challenging but important future direction with potential real-world applications.
More visual insights#
More on figures
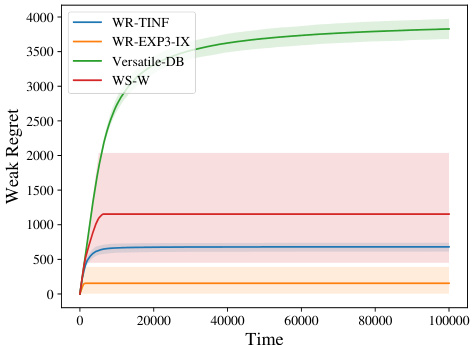
🔼 The figure shows the performance of four algorithms (WR-TINF, WR-EXP3-IX, Versatile-DB, and WS-W) in three different scenarios. Scenario 1 features a small number of arms and satisfies the strong stochastic transitivity (SST) assumption. Scenario 2 uses a moderate number of arms and does not satisfy SST, while Scenario 3 features a large number of arms and also does not satisfy SST. For each scenario, the figure presents plots showing weak regret over time (in rounds). The plots include mean regret and 0.2 and 0.8 quantiles to illustrate the variability of the algorithms’ performance. The results show that the algorithms’ performance varies across the different scenarios, highlighting the impact of the number of arms and the SST property on the effectiveness of different strategies for minimizing weak regret.
read the caption
Figure 1: Performance of algorithms in different scenarios
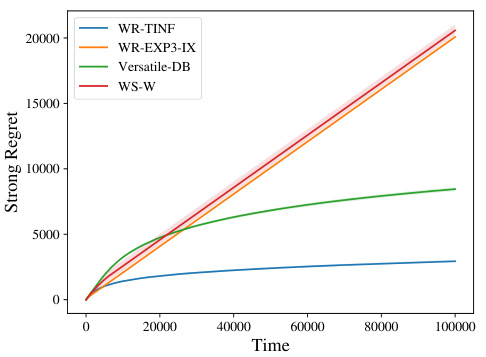
🔼 This figure presents a comparison of the performance of four algorithms for dueling bandits across three scenarios. Each scenario varies in the number of arms (K) and whether the strong stochastic transitivity (SST) property holds. The algorithms compared are WR-TINF, WR-EXP3-IX, Versatile-DB, and WS-W. The plots show mean weak regret (except for Figure 1c which shows strong regret) with 0.2 and 0.8 quantiles over 20 iterations. The results highlight how the optimal algorithm changes depending on the problem characteristics (size and structure of the gap matrix, SST property).
read the caption
Figure 1: Performance of algorithms in different scenarios
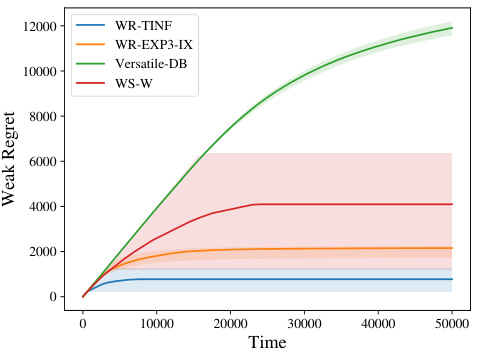
🔼 This figure compares the performance of four algorithms (WR-TINF, WR-EXP3-IX, Versatile-DB, and WS-W) for minimizing weak regret in three different dueling bandit problem settings: small problem with SST, moderate problem without SST, and large problem without SST. Each scenario varies in the number of arms and the structure of the preference probabilities, testing different conditions to highlight the relative strengths and weaknesses of each algorithm. The plots show the mean weak regret over 20 iterations, along with 0.2 and 0.8 quantiles to visualize the variability. This helps illustrate which algorithms are optimal under which conditions, particularly with respect to the tradeoff between exploration and exploitation in relation to the gap between the Condorcet winner and suboptimal arms.
read the caption
Figure 1: Performance of algorithms in different scenarios
Full paper#



















