↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Graph Neural Networks (GNNs) are susceptible to adversarial attacks, and existing defense mechanisms often prove inadequate, especially against adaptive attacks that directly target the victim model. This is largely due to inherent estimation bias within many popular l1-based robust GNNs. These biases accumulate as attack budgets increase, ultimately undermining the effectiveness of these defenses.
This research introduces RUNG, a novel GNN architecture that addresses these shortcomings. RUNG employs a robust and unbiased graph signal estimator, mitigating estimation bias. This is achieved through an efficient Quasi-Newton Iterative Reweighted Least Squares algorithm, which is readily integrated into the GNN architecture as unbiased aggregation layers. Extensive experiments show that RUNG offers considerably improved robustness against adaptive attacks compared to state-of-the-art methods, showcasing its potential for enhanced security in real-world applications.
Key Takeaways#
Why does it matter?#
This paper is crucial because it addresses the critical vulnerability of Graph Neural Networks (GNNs) to adversarial attacks. Current defenses often fail under adaptive attacks, limiting GNNs’ real-world applications. The proposed RUNG model offers a significant advancement by achieving strong robustness while maintaining high accuracy, opening new avenues for secure GNN development and deployment in various domains.
Visual Insights#
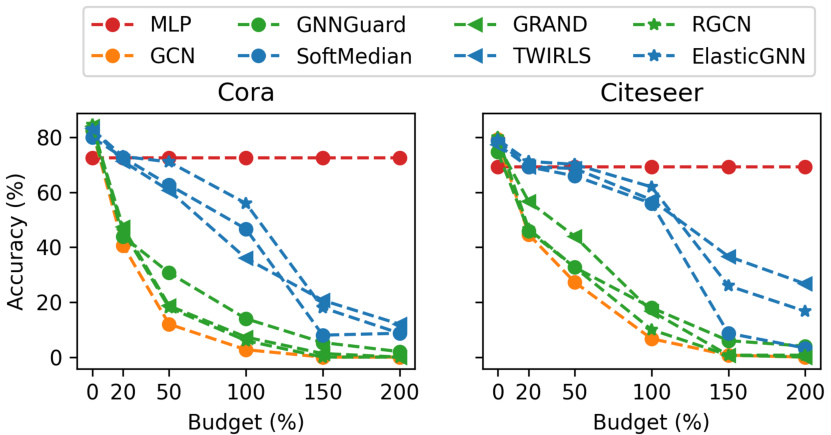
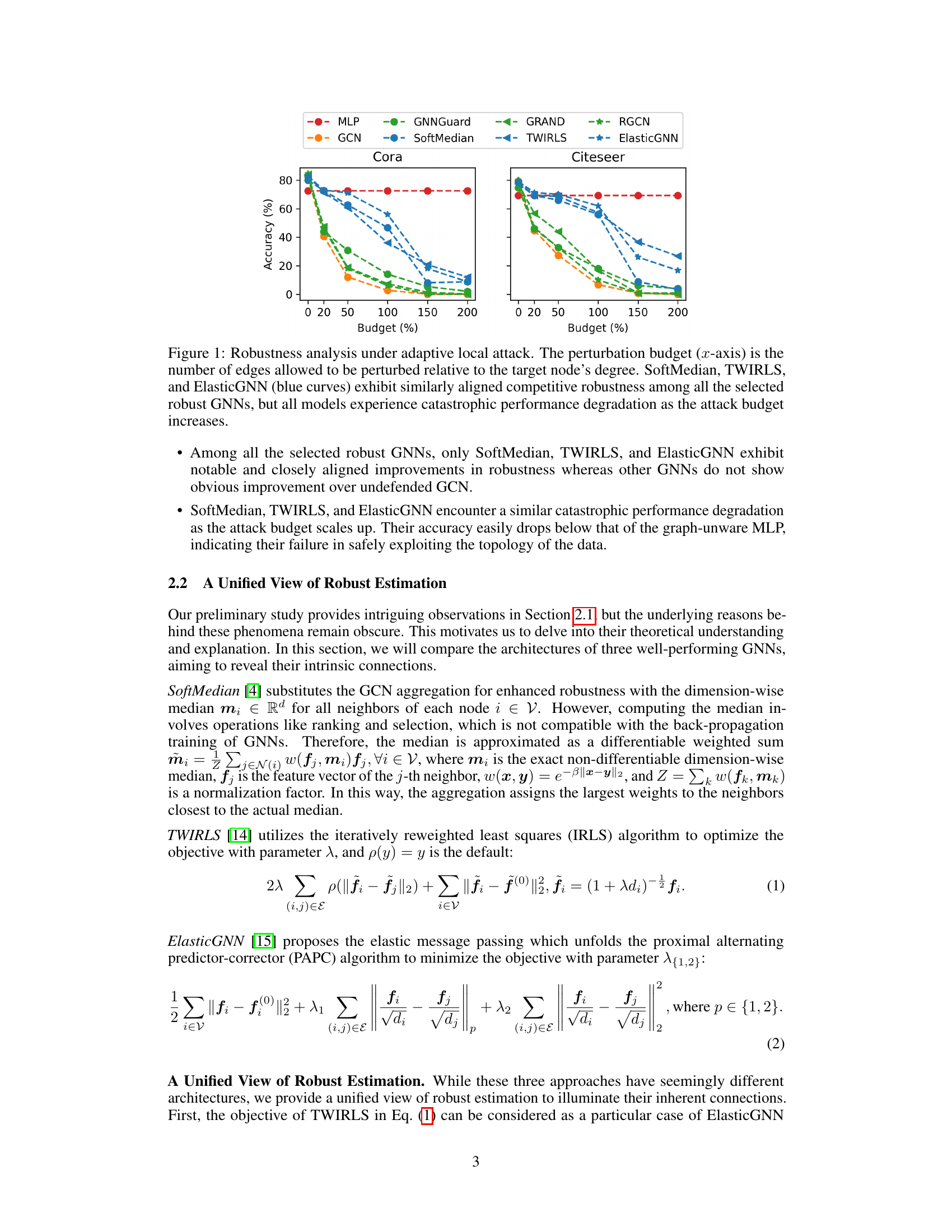
The figure shows the robustness of several graph neural networks (GNNs) against adaptive local attacks. The x-axis represents the percentage of edges perturbed relative to the target node’s degree, which acts as a measure of attack strength. The y-axis shows the classification accuracy of the GNNs. The results indicate that SoftMedian, TWIRLS, and ElasticGNN exhibit similar and relatively higher robustness initially but all selected GNNs show a catastrophic drop in accuracy as the attack budget increases.
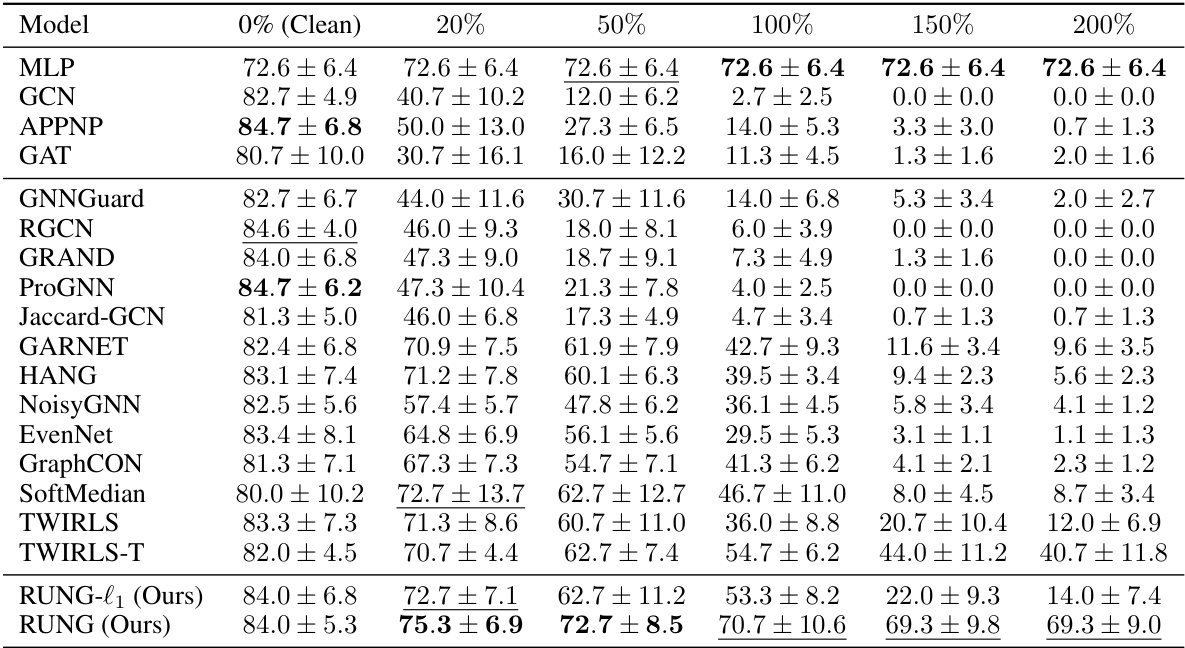
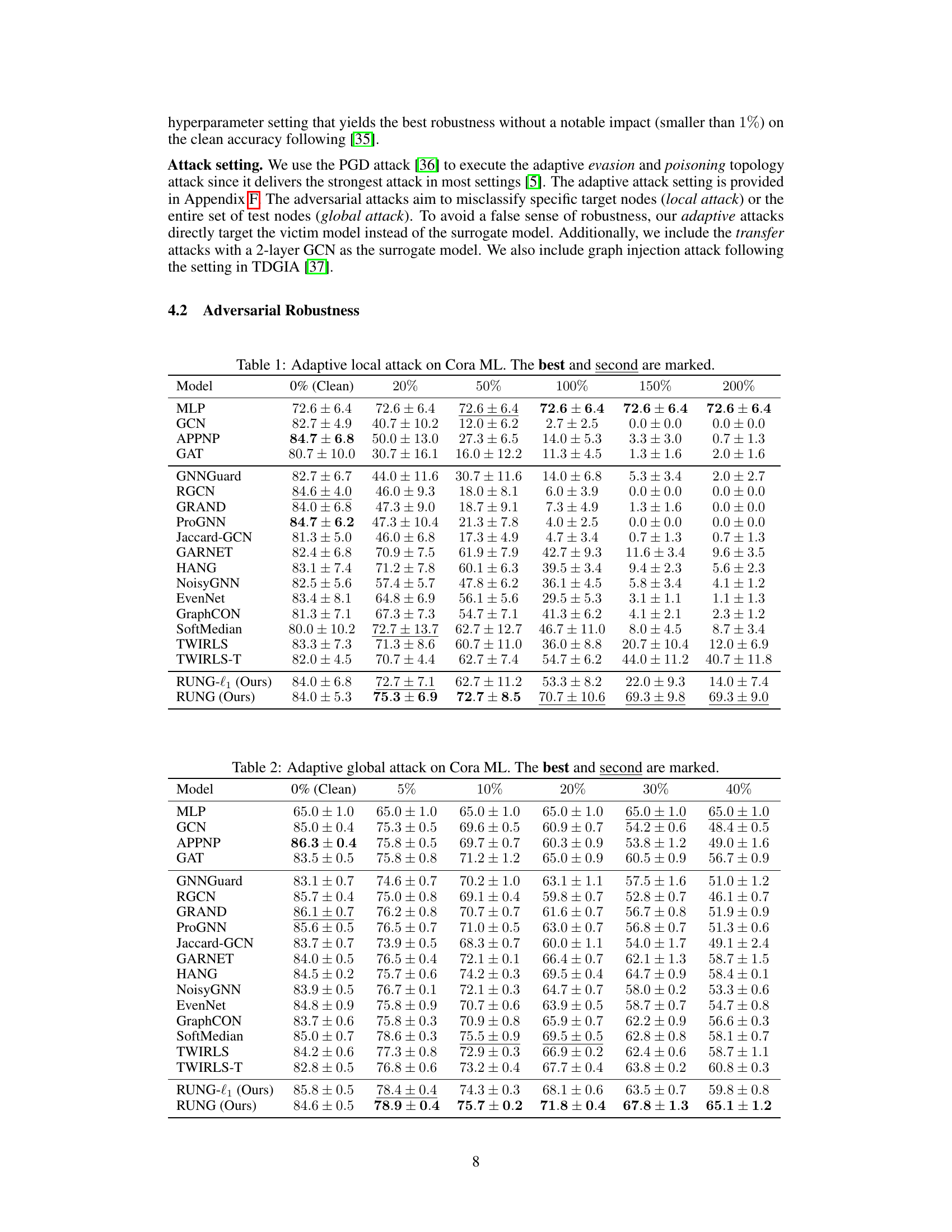
This table presents the results of an adaptive local attack on the Cora ML dataset. The attack is designed to misclassify specific target nodes (local attack) by perturbing the graph structure. The table shows the accuracy of different graph neural network (GNN) models under varying attack budgets (percentage of edges allowed to be perturbed relative to the target node’s degree). The performance of various GNNs and baseline methods are listed under varying attack strength, from 0% (clean) to 200%. The best and second-best performing models for each attack budget are highlighted.
In-depth insights#
Robustness Analysis#
A Robustness Analysis section in a research paper would critically examine the resilience of a model or system to various attacks or perturbations. It would likely involve a detailed methodology, clearly defining the types of attacks considered (e.g., adversarial examples, data poisoning, or model modifications). Key aspects would include quantitative evaluation using metrics relevant to the specific application, as well as qualitative analysis explaining the model’s vulnerabilities and the mechanisms of attack. A robust analysis might compare the performance against baseline models, showcasing the model’s strengths and weaknesses relative to existing solutions. Statistical significance of any reported results would be crucial, addressing the reproducibility and generalizability of findings. The analysis should encompass a discussion of the limitations of the methods and potential improvements for future research, ultimately providing a comprehensive understanding of the model’s robustness and areas needing further investigation.
Bias in l1 Models#
The analysis of ‘Bias in l1 Models’ within the context of graph neural networks (GNNs) reveals a crucial limitation of existing robust GNNs. These models, while initially demonstrating improved robustness against adversarial attacks compared to their l2 counterparts, exhibit a significant performance degradation as attack budgets increase. This degradation stems from the inherent estimation bias associated with l1-based graph signal smoothing. The l1 penalty, while effective in mitigating the influence of outliers, also shrinks coefficients towards zero, thereby accumulating bias as more adversarial perturbations are introduced. This bias, amplified with increasing attack budgets, leads to the observed catastrophic performance drop. A robust and unbiased estimator is proposed to address this limitation, mitigating the bias and achieving significantly improved robustness while maintaining accuracy. The findings highlight the importance of a thorough robustness analysis, going beyond simple transfer attacks to encompass more challenging adaptive attacks, for a comprehensive understanding of GNN vulnerability.
QN-IRLS Algorithm#
The Quasi-Newton Iteratively Reweighted Least Squares (QN-IRLS) algorithm is a crucial contribution of the paper, designed to efficiently solve the non-smooth and non-convex optimization problem posed by the Robust and Unbiased Graph Signal Estimator (RUGE). QN-IRLS cleverly approximates the computationally expensive inverse Hessian matrix using a diagonal matrix, thereby significantly accelerating convergence without requiring the selection of a step size, a common challenge in traditional IRLS methods. This efficiency is critical for enabling the unfolding of the algorithm into robust unbiased aggregation layers within Graph Neural Networks (GNNs). The algorithm’s ability to handle non-smooth penalties like the Minimax Concave Penalty (MCP), combined with its efficiency, makes it particularly well-suited for enhancing the robustness of GNNs against adversarial attacks. The theoretical guarantees provided for QN-IRLS convergence further solidify its value as a reliable and efficient optimization technique within the proposed GNN architecture, contributing to the model’s strong performance and interpretability.
RUNG Architecture#
The RUNG architecture is a novel approach to building robust and unbiased graph neural networks (GNNs). It addresses the limitations of existing robust GNNs by mitigating estimation bias in graph signal processing. The core innovation lies in its unbiased aggregation layers, which are unfolded from an efficient Quasi-Newton Iteratively Reweighted Least Squares (QN-IRLS) algorithm. This algorithm solves a robust and unbiased graph signal estimation problem, directly addressing the accumulation of bias observed in prior methods under adaptive attacks. The use of MCP (Minimax Concave Penalty) is crucial, providing a balance between robustness and unbiasedness. The architecture is theoretically grounded, with proofs of convergence for the QN-IRLS algorithm. Importantly, RUNG’s design allows for interpretability, with clear connections to existing GNN architectures and the ability to cover them as special cases. Ultimately, RUNG offers a significant step towards building truly robust GNNs by directly tackling estimation bias, a previously overlooked problem hindering the widespread deployment of GNNs in sensitive applications.
Future Research#
Future research directions stemming from this work could explore several promising avenues. Extending the unbiased aggregation framework to handle heterophily in graphs is crucial, as many real-world networks exhibit this property. The current model’s performance on heterophilic graphs warrants further investigation and potential modifications. Another key area is developing more sophisticated algorithms to address the non-convexity of the optimization problem. While Quasi-Newton IRLS offers efficiency gains, more advanced methods could further enhance convergence and scalability. Analyzing the robustness of RUNG against different attack strategies beyond those considered in the study is also vital. This would involve a more extensive evaluation under various attack budgets and model architectures. Furthermore, investigating the theoretical limits of the proposed method in terms of its robustness guarantees and generalization abilities is needed to better understand its fundamental strengths and weaknesses. Finally, exploring applications of RUNG in new domains, such as temporal graphs or dynamic networks, would demonstrate its broad applicability and highlight its practical value in solving complex real-world problems.
More visual insights#
More on figures

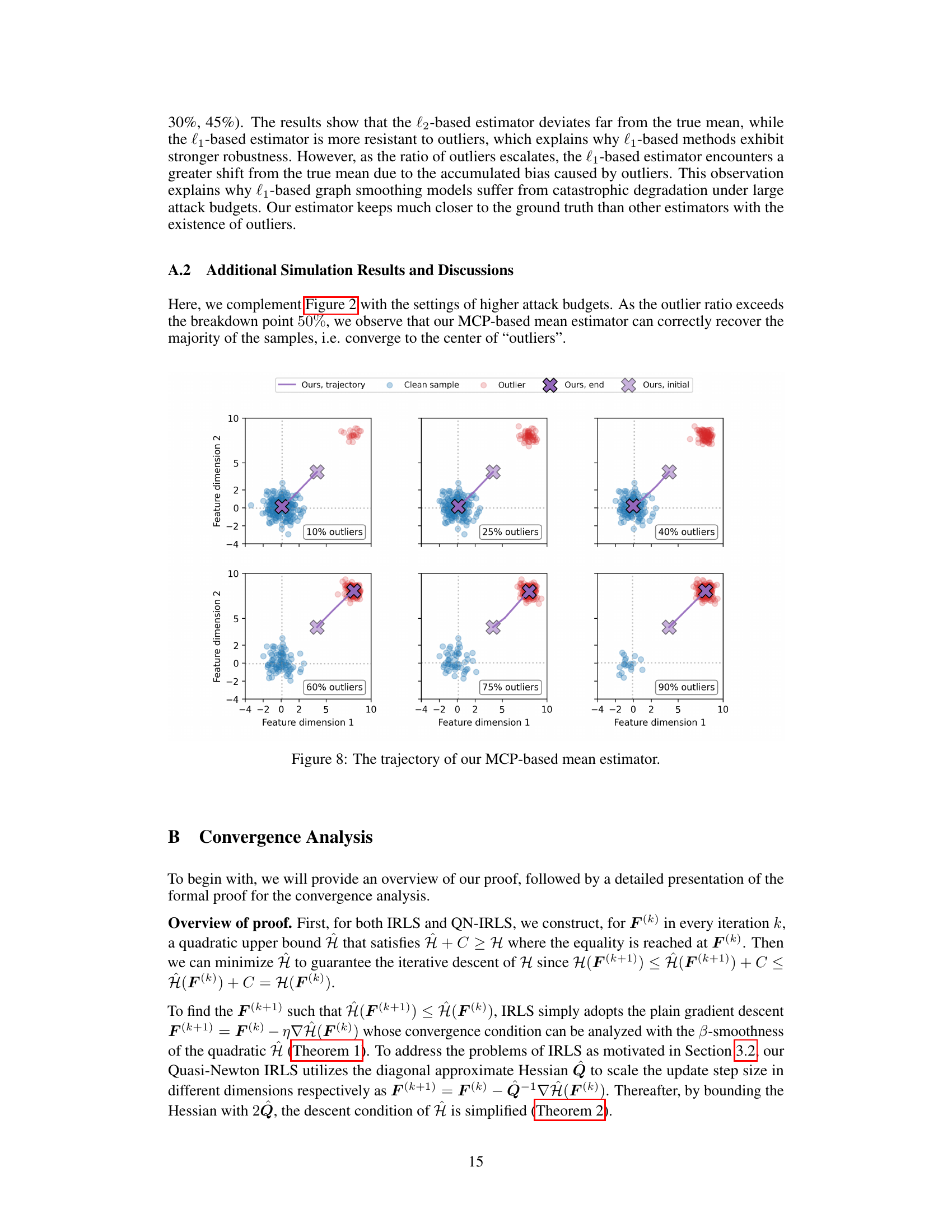
This figure compares different mean estimators (l1, l2, and the proposed method) in the presence of outliers. It shows that the l1 estimator is more robust to outliers than the l2 estimator, but still suffers from bias as the number of outliers increases. The proposed method is shown to be more robust and less biased than both l1 and l2 estimators.
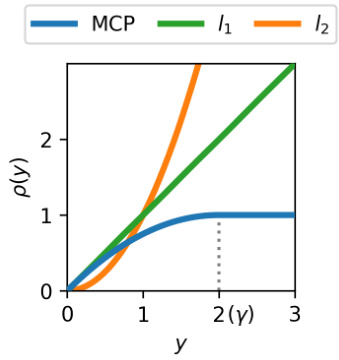
This figure compares three penalty functions: MCP (blue), l1 (green), and l2 (orange). The MCP penalty function is a non-convex function that approximates the l1 norm for small values of y and becomes constant for larger values of y. This property helps mitigate estimation bias in the presence of outliers and enhances the robustness of the model. The l1 penalty is a linear function that is robust to outliers but can induce estimation bias, whereas the l2 penalty is a quadratic function that is less robust to outliers but has desirable mathematical properties. The figure shows how the MCP penalty balances these properties, combining the robustness of l1 and the mathematical convenience of l2.
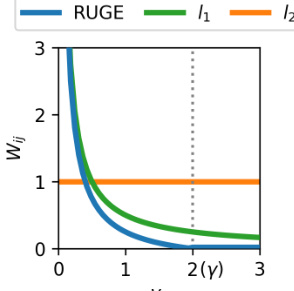
The figure shows a comparison of three penalty functions used in graph signal smoothing: RUGE (Robust and Unbiased Graph signal Estimator), l1, and l2. The x-axis represents the magnitude of the feature difference between adjacent nodes (y), while the y-axis represents the penalty value (Wij). RUGE is a hybrid approach combining properties of l1 and l2, providing a balance between robustness and unbiasedness. The vertical dotted line indicates a threshold (γ) where the behavior of RUGE transitions from a sharp penalty (similar to l1) to a flatter penalty (similar to l2).

The figure shows the robustness of different graph neural networks (GNNs) against adaptive local attacks. The x-axis represents the percentage of edges perturbed relative to the target node’s degree, and the y-axis represents the node classification accuracy. The results show that SoftMedian, TWIRLS, and ElasticGNN perform similarly and better than other methods initially, but their performance drops significantly as the attack budget increases. This demonstrates the vulnerability of these models to adaptive attacks.

This figure compares different mean estimators (l2, l1, and the proposed MCP-based estimator) under different outlier ratios. It demonstrates that the l1-based estimator is more robust to outliers than the l2-based estimator, but it still suffers from bias as the outlier ratio increases. The proposed MCP-based estimator is shown to be less susceptible to this bias.
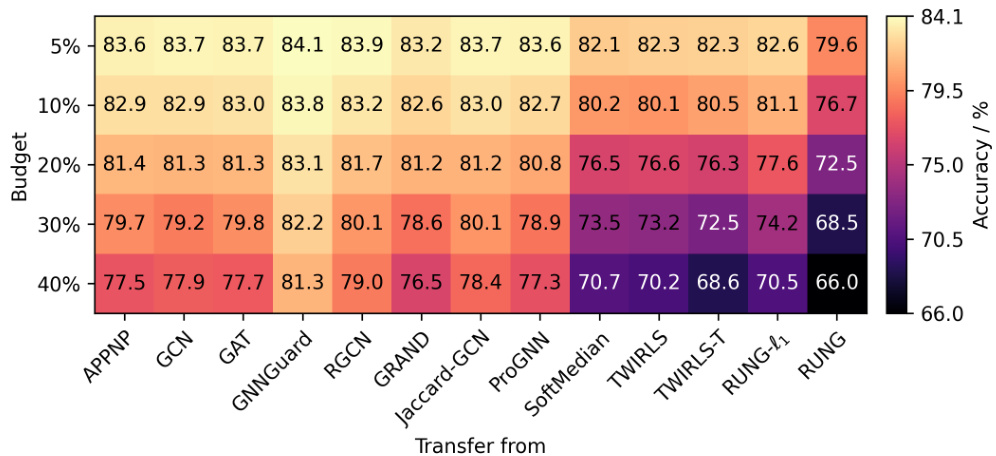
The figure shows the robustness of several GNN models against adaptive local attacks. The x-axis represents the percentage of edges perturbed relative to the target node’s degree, simulating different attack strengths. The y-axis shows the classification accuracy. SoftMedian, TWIRLS, and ElasticGNN exhibit similar, relatively high robustness initially, but their performance drastically decreases as the attack budget increases, eventually performing worse than a simple MLP (which doesn’t use graph structure). Other GNN models show less improvement and similar performance degradation.

This figure shows the robustness of various graph neural networks (GNNs) against adaptive local attacks. The x-axis represents the attack budget (percentage of edges perturbed relative to the node degree), and the y-axis represents the accuracy of the GNNs. The results show that SoftMedian, TWIRLS, and ElasticGNN exhibit relatively better robustness compared to other GNNs, but their performance degrades significantly as the attack budget increases.
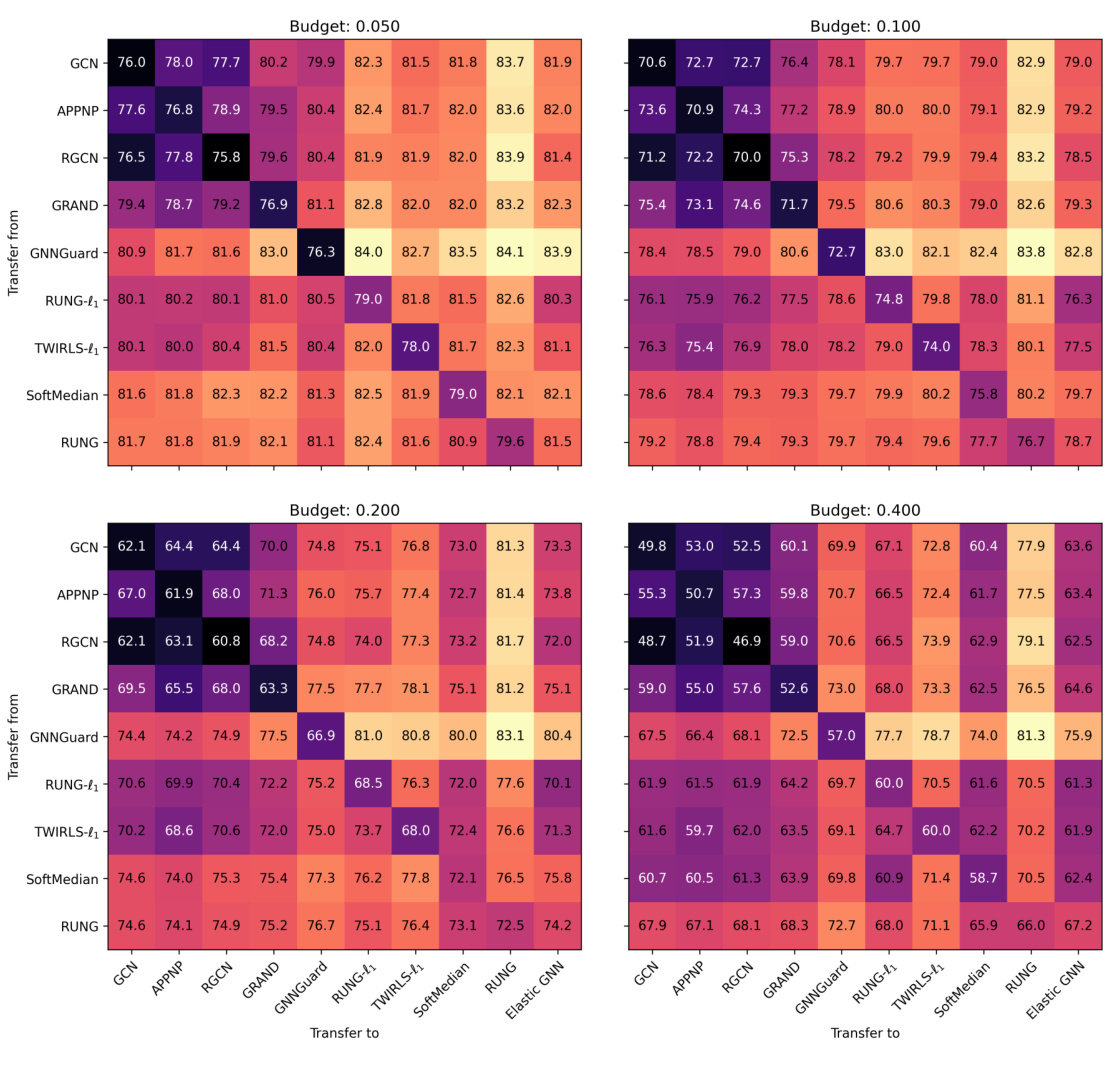
This figure presents the results of a robustness analysis conducted on several Graph Neural Networks (GNNs) under adaptive local attacks. The x-axis represents the attack budget (percentage of edges perturbed relative to the node’s degree), and the y-axis shows the node classification accuracy. The results indicate that while SoftMedian, TWIRLS, and ElasticGNN show better initial robustness than other GNNs, all models eventually exhibit a significant drop in performance as the attack budget increases, underperforming a simple Multilayer Perceptron (MLP) that does not consider graph topology.

This figure shows the robustness of several GNN models against adaptive local attacks. The x-axis represents the percentage of edges perturbed relative to the degree of the target node. The y-axis represents the accuracy of node classification. The figure highlights that while SoftMedian, TWIRLS, and ElasticGNN show initially better robustness than other models, their performance sharply decreases as the attack budget increases, eventually performing worse than graph-agnostic MLPs.

This figure shows how the accuracy of the RUNG model changes as the number of aggregation layers increases under different attack budgets (5%, 10%, 20%, 40%). It demonstrates the convergence behavior of the QN-IRLS algorithm within the RUNG architecture. As the number of layers increases, the accuracy tends to improve, especially under higher attack budgets. The results suggest that a sufficient number of layers is necessary for the model to converge and achieve optimal robustness.

This figure shows the robustness of various GNN models against adaptive local attacks. The x-axis represents the percentage of edges perturbed relative to the node’s degree, simulating the attack budget. The y-axis shows the node classification accuracy. SoftMedian, TWIRLS, and ElasticGNN show initially better robustness than other models, but their performance degrades significantly as the attack budget increases, eventually performing worse than graph-agnostic MLPs.
More on tables
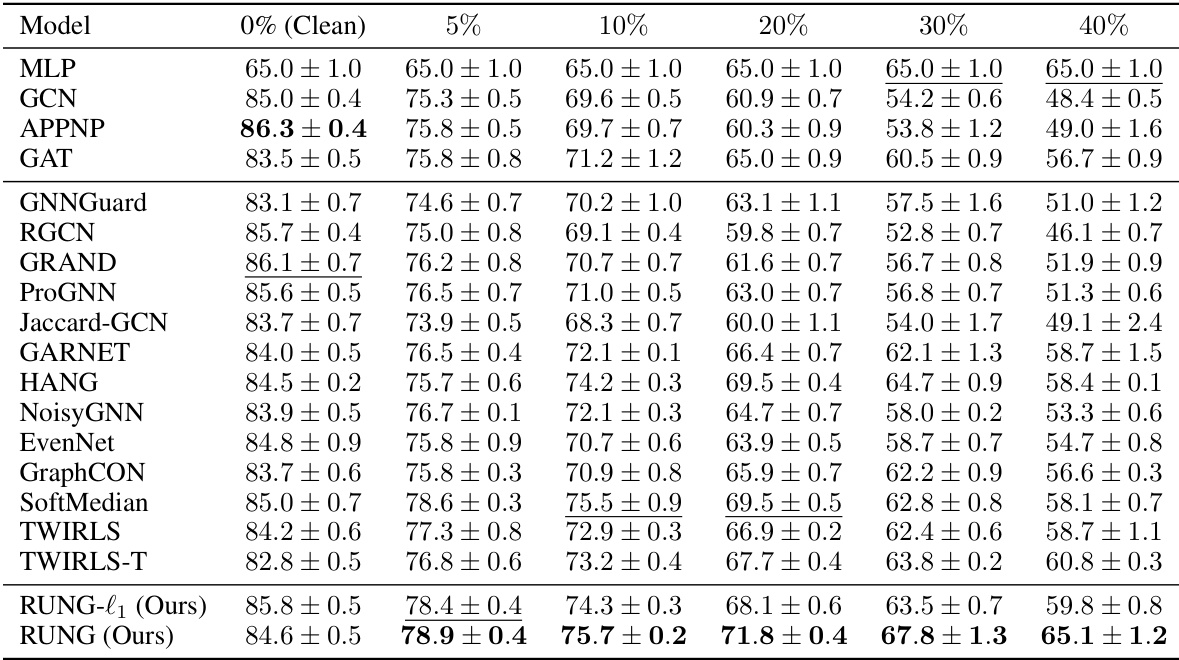
This table presents the results of an adaptive local attack on the Cora ML dataset. The attack involves perturbing a limited number of edges near the target node. The table shows how various graph neural network (GNN) models, both standard and robust, perform under this attack, as measured by node classification accuracy. The percentage of edges allowed to be perturbed is given on the x-axis, with performance degradation shown as the attack budget increases. The best and second-best performing models are marked for each perturbation level.
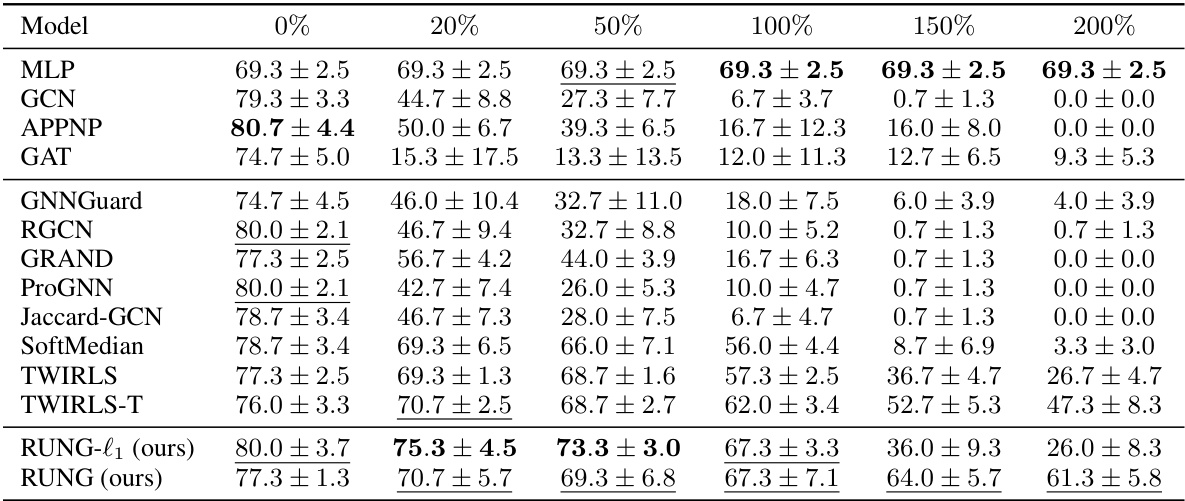
This table presents the results of an adaptive local attack on the Cora ML dataset. It shows the performance (accuracy) of various GNN models, including both standard and robust models, under different attack budgets (percentage of edges perturbed relative to the target node’s degree). The best and second-best performing models for each budget are highlighted. The goal is to demonstrate the robustness (or lack thereof) of different GNN architectures against adaptive attacks, where the attacker adjusts its strategy based on the model’s response.

This table presents the results of an adaptive local attack on the Cora ML dataset. The experiment measures the robustness of various graph neural network (GNN) models against adversarial attacks by gradually increasing the attack budget (percentage of edges allowed to be perturbed relative to the target node’s degree). The table shows the classification accuracy of each model at different attack budget levels (0%, 20%, 50%, 100%, 150%, 200%). The best and second-best performing models for each budget are highlighted.
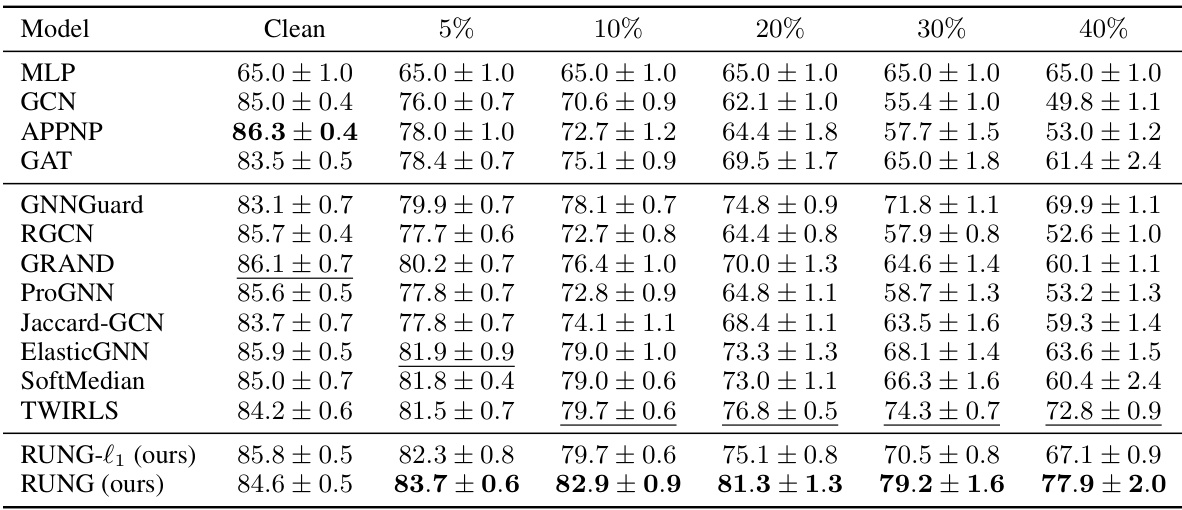
This table presents the results of a global adaptive attack on the Cora ML dataset. The attack perturbs the graph structure to adversarially affect node classification accuracy. The table shows the performance (accuracy ± standard deviation) of various GNN models (including the proposed RUNG) at different attack budgets (percentage of perturbed edges). The best and second-best performing models for each budget are highlighted.

This table presents the results of an adaptive local attack on the Cora ML dataset. The attack is designed to perturb the graph structure locally around target nodes, and its effectiveness is measured by the classification accuracy under different attack budgets (percentage of allowed edge perturbations). The table compares the performance of various GNN models, including standard models and robust defenses, demonstrating their resilience to the attack and highlighting the top-performing models.
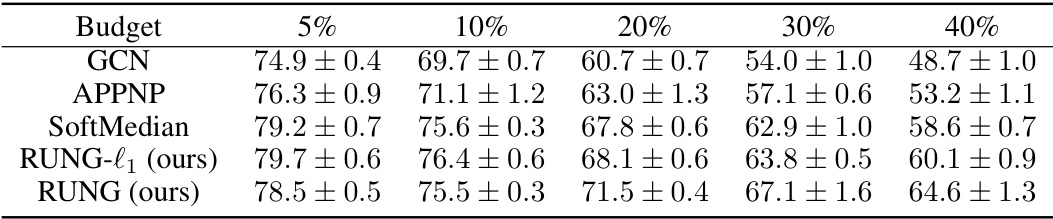
This table presents the results of a global adaptive attack on the Cora ML dataset. The experiment evaluates the robustness of various graph neural network (GNN) models against this attack. The ‘Budget’ column represents the percentage of edges that were perturbed in the graph. The remaining columns show the classification accuracy (with standard deviation) of each model under varying attack budgets. The best-performing models for each attack budget are marked.

This table presents the results of poisoning attacks on the Cora ML dataset. It shows the classification accuracy (%) of different GNN models (GCN, APPNP, SoftMedian, RUNG-l1, and RUNG) under various poisoning attack budgets (5%, 10%, 20%, 30%, and 40%). The results demonstrate the robustness of the RUNG models against poisoning attacks, showing higher accuracy than other models, especially as the attack budget increases.

This table presents the results of global PGD attacks on the large-scale Ogbn- Arxiv dataset. It compares the performance of GCN, APPNP, SoftMedian, RUNG-l1 (a variant of RUNG using the l1 penalty), and RUNG (the proposed model) under different attack intensities (1%, 5%, and 10%). The ‘Clean’ column shows the accuracy without any attack. The results demonstrate the relative robustness of the different models against these attacks.

This table compares the performance of RUNG under normal training and adversarial training against adaptive attacks with varying budgets (5%, 10%, 20%, 30%, 40%). The results show the accuracy of the model on the clean data and under attack with different attack budgets. Adversarial training improves the model’s robustness against attacks.
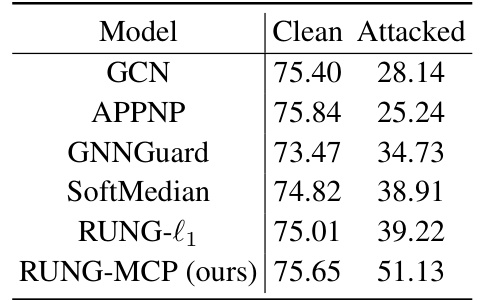
This table presents the results of a graph injection attack on the Citeseer dataset. The ‘Clean’ column shows the accuracy of each model on clean data, while the ‘Attacked’ column shows the accuracy after a graph injection attack. The models compared include GCN, APPNP, GNNGuard, SoftMedian, RUNG-l1, and RUNG-MCP (the proposed model). The table demonstrates the relative robustness of each model against graph injection attacks, showing that RUNG-MCP outperforms other models in maintaining accuracy after the attack.

This table presents a comparison of the performance of different models on the Cora dataset under adaptive attacks. The models compared include RUNG-l1 (using the l1 penalty), RUNG (using the MCP penalty), RUNG-l1-GCN (l1 penalty applied to GCN), and RUNG-GCN (MCP penalty applied to GCN). The performance is measured by accuracy under different attack budgets (0%, 5%, 10%, 20%, 30%, 40%). This allows a comparison of the robustness of the models with different penalty functions and GCN architectures.

This table presents the results of an adaptive local attack on the Cora ML dataset. It compares the performance of various graph neural network (GNN) models, including baselines and robust GNNs, at different attack budgets (percentage of edges perturbed relative to a node’s degree). The models’ node classification accuracy is shown, illustrating their robustness against adaptive attacks. The best and second-best performing models for each attack budget are highlighted.
Full paper#