TL;DR#
Many studies show that using public data for pre-training improves differentially private model training. However, most of these studies focus on in-distribution tasks and do not address settings where there is distribution shift between pre-training and fine-tuning data. This is a major limitation because in real world scenarios private data is often fundamentally different from the public datasets. This paper addresses this limitation by conducting empirical studies on three tasks, and shows that public features can significantly improve the accuracy of private training even in the presence of large distribution shift. This improvement is not just observed empirically, but it is also theoretically explained in the paper through a stylized theoretical model.
The paper proposes a two-stage algorithm that first estimates the shared, low-dimensional representation from public data using a method of moments estimator, and then performs private linear regression within the learned subspace using the private data. By leveraging dimensionality reduction, the algorithm achieves better sample complexity. The paper also provides a novel lower bound that demonstrates the optimality of their approach among algorithms that estimate the transfer parameters within the same low-dimensional subspace. The findings show that pre-trained features can improve private learning, even under extreme distribution shift, and that linear probing consistently outperforms private finetuning.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in private AI, particularly those working on federated learning and transfer learning. It directly addresses the limitations of prior work that only considers in-distribution tasks, offering a novel theoretical model and empirical evidence for improving private training under realistic distribution shifts. This opens up new avenues for building more robust and practical privacy-preserving AI systems that can leverage publicly available data while safeguarding sensitive information.
Visual Insights#
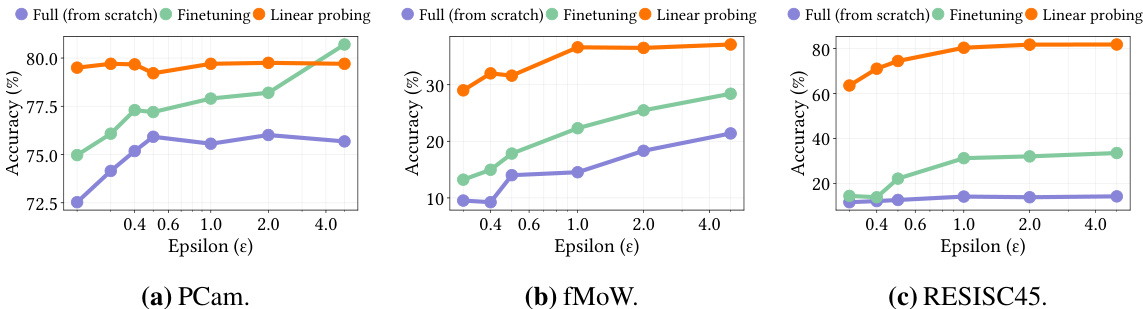
🔼 This figure shows the results of private training on three different datasets (PCam, fMoW, and RESISC45) using three different training methods (full training from scratch, full finetuning, and linear probing). For each dataset and training method, the accuracy is plotted against different levels of privacy (epsilon). The figure highlights that linear probing consistently outperforms the other two methods, especially when the privacy level is low, illustrating the benefits of using public pre-trained features even under high distribution shifts between public and private data.
read the caption
Figure 1: Private training on three datasets. (a) PCam is a binary classification task on which private training from scratch achieves relatively high accuracy, but linear probing on the pretrained model still improves accuracy up to 4%. (b) The fMoW model trained from scratch is unusable at low privacy levels while linear probing achieves close to nonprivate accuracy. (c) On RESISC45, linear probing outperforms full finetuning by over 50% at all ε levels.
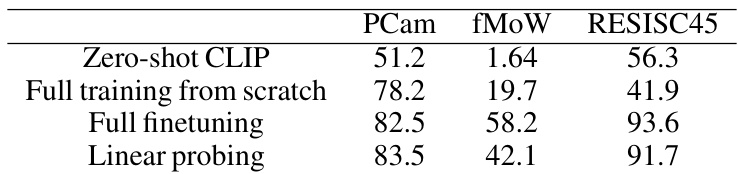
🔼 This table presents the non-private test accuracy results for three different training methods on three datasets: PCam, fMoW, and RESISC45. The methods are zero-shot using CLIP (no training on the specific dataset), training from scratch (training a model only on the private dataset), full finetuning (pretraining on public data then finetuning on private data), and linear probing (using pretrained features and a linear classifier on private data). The results demonstrate the effectiveness of using public pretrained features, especially with linear probing, even in scenarios with large distribution shifts between public and private data.
read the caption
Table 1: Test accuracy of nonprivate training on each dataset that we evaluate.
In-depth insights#
Private Transfer Learning#
Private transfer learning tackles the challenge of leveraging publicly available data to enhance the performance of models trained on sensitive, private data while preserving privacy. The core idea is to pre-train a model on a large public dataset, transferring the learned representations to a smaller, private dataset for fine-tuning. This approach aims to mitigate the limitations of training solely on private data, which often suffers from insufficient samples leading to poor accuracy. However, distribution shifts between public and private data pose a significant hurdle. The success of private transfer learning hinges on the extent to which public data’s representations generalize to the private data’s characteristics. Effective techniques must address the challenges of privacy-preserving transfer, and careful consideration is needed to choose suitable public datasets that minimize the risk of privacy leakage.
Public Data Benefits#
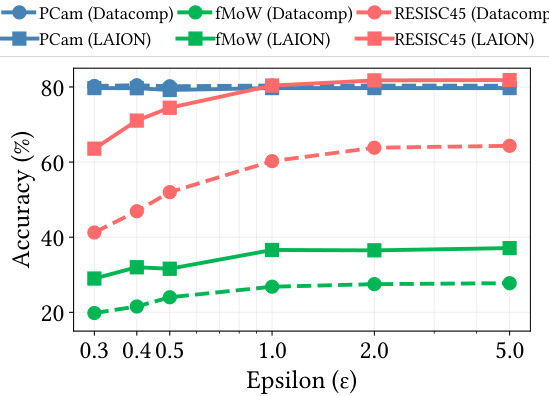
The concept of leveraging public data to enhance private model training, particularly under distribution shift, offers significant advantages. The core benefit lies in improved sample complexity: public data, even if insufficient for directly solving the private task, can help learn a shared low-dimensional representation between public and private datasets. This shared representation allows for more efficient private training, reducing the amount of private data needed to achieve reasonable accuracy. The method effectively addresses challenges posed by limited private data and significant distribution shift, showing that public pretraining can improve the performance even when zero-shot performance on the private task is exceptionally poor, demonstrating its practical value in sensitive applications where complete privacy is not achievable through zero-shot methods alone. Linear probing, a simpler approach than full model finetuning, proves highly effective when using public representations, offering a balance between accuracy and resource efficiency in the private setting.
Out-of-Distribution Shift#
The concept of “Out-of-Distribution Shift” in machine learning refers to the scenario where the distribution of data used for training a model differs significantly from the distribution of data encountered during the model’s deployment. This is a crucial challenge because models trained on one distribution often perform poorly when presented with data from a different distribution. The paper addresses this challenge in the context of private transfer learning, focusing on situations where private (sensitive) data is scarce and the distribution of public (non-sensitive) data differs considerably from the private data’s distribution. It explores how effectively leveraging features from publicly available data can still boost the performance of models trained on private, limited data, even under extreme out-of-distribution conditions. The research highlights that even with a large distribution shift, public representations improve accuracy, which has significant implications for making private model training more practical.
Linear Probing Wins#
The assertion ‘Linear Probing Wins’ within the context of private transfer learning under distribution shift suggests that a simpler model, linear probing, outperforms more complex approaches like full finetuning when leveraging publicly available data to enhance the performance of a differentially private model trained on sensitive data. This is a significant finding because full finetuning often incurs a substantial computational cost, requires substantial memory, and increases the risk of privacy violations. Linear probing’s superior efficiency and its comparable or better accuracy in this setting are crucial advantages. The effectiveness of linear probing highlights the potential for efficient privacy-preserving techniques that can still achieve high levels of accuracy, even when dealing with significant distribution shifts between the public and private datasets. The core idea is that, by effectively utilizing pre-trained features from a public model, linear probing can achieve strong performance with reduced privacy risk. Therefore, the ‘win’ is not merely about enhanced accuracy but also about the superior efficiency, reduced computational cost, and improved privacy-preservation, which are all paramount in private transfer learning contexts. This is a highly insightful finding and has profound implications for practical applications.
Subspace Theory#
Subspace theory, in the context of this research paper, offers a powerful lens for understanding the effectiveness of leveraging publicly available data to improve the accuracy of privately trained models, especially in scenarios with significant distribution shifts between public and private datasets. The core idea revolves around the assumption that the relevant features for both public and private tasks reside within a shared low-dimensional subspace. This means that even if the public and private datasets appear vastly different in their high-dimensional representations, their crucial information lies in a lower dimensional space that can be effectively learned from the public data. This subspace is not necessarily explicitly learned but implicitly captured by utilizing pretrained feature extractors (like the CLIP model used in this work). Once the low-dimensional representation is estimated, private training can be conducted in this reduced space, thus improving the sample complexity and mitigating the challenges associated with limited private data while maintaining differential privacy guarantees. This theoretical framework provides valuable insight into why public pretraining can significantly improve accuracy in situations where zero-shot performance from public data alone is unacceptably low, offering a rigorous explanation for the empirical findings reported in the paper.
More visual insights#
More on figures
🔼 This figure shows the results of private training on three datasets: PCam, fMoW, and RESISC45. Each dataset shows test accuracy (y-axis) as a function of privacy level (ε on the x-axis) for three approaches: training from scratch, finetuning a pretrained model, and linear probing with pretrained features. The figure highlights that linear probing consistently outperforms both training from scratch and full finetuning, particularly at lower privacy levels (higher ε). The results demonstrate the benefit of using pretrained public features for private training even when there’s a significant distribution shift between the public and private datasets.
read the caption
Figure 1: Private training on three datasets. (a) PCam is a binary classification task on which private training from scratch achieves relatively high accuracy, but linear probing on the pretrained model still improves accuracy up to 4%. (b) The fMoW model trained from scratch is unusable at low privacy levels while linear probing achieves close to nonprivate accuracy. (c) On RESISC45, linear probing outperforms full finetuning by over 50% at all ε levels.
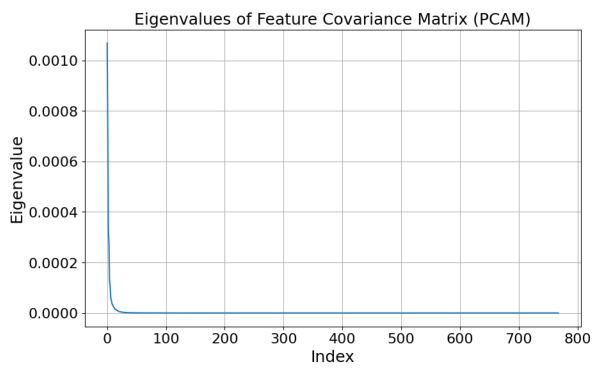
🔼 This figure displays the eigenspectra of the feature covariance matrices for three datasets (PCam, fMoW, and RESISC45). The eigenspectra are derived from features extracted using a pretrained CLIP ViT-B/32 model. The plots visually demonstrate the distribution of eigenvalues, showing how quickly the eigenvalues decay for each dataset. This decay rate suggests that the data lies in a low-dimensional subspace, supporting the theoretical model of the paper that assumes a shared low-dimensional subspace between public and private tasks, even in cases of extreme distribution shift.
read the caption
Figure 5: Eigenspectra of feature covariance matrices for features extracted from pretrained CLIP ViT-B/32 model.
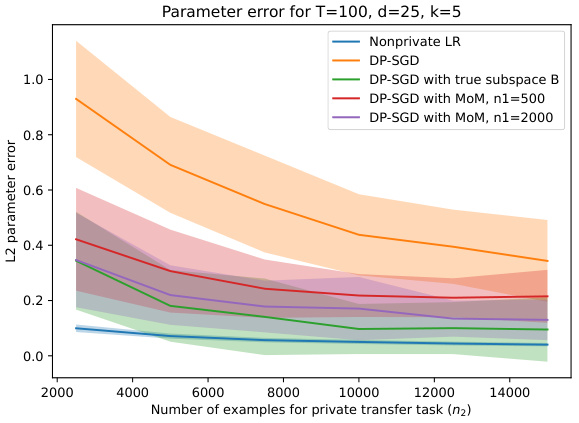
🔼 This figure empirically validates the theoretical model proposed in Section 5.1. It shows the L2 parameter error for different private training methods across varying numbers of private examples (n2). The methods include non-private linear regression (Nonprivate LR), differentially private stochastic gradient descent (DP-SGD) with and without prior subspace estimation using different numbers of public examples (n1=500 and n1=2000). The results demonstrate that incorporating public data (using Method of Moments (MoM) for subspace estimation) effectively reduces the error in private linear regression, approaching the performance of DP-SGD with the true subspace known. The shaded areas represent confidence intervals.
read the caption
Figure 4: Empirical verification of setup described in Section 5.1.
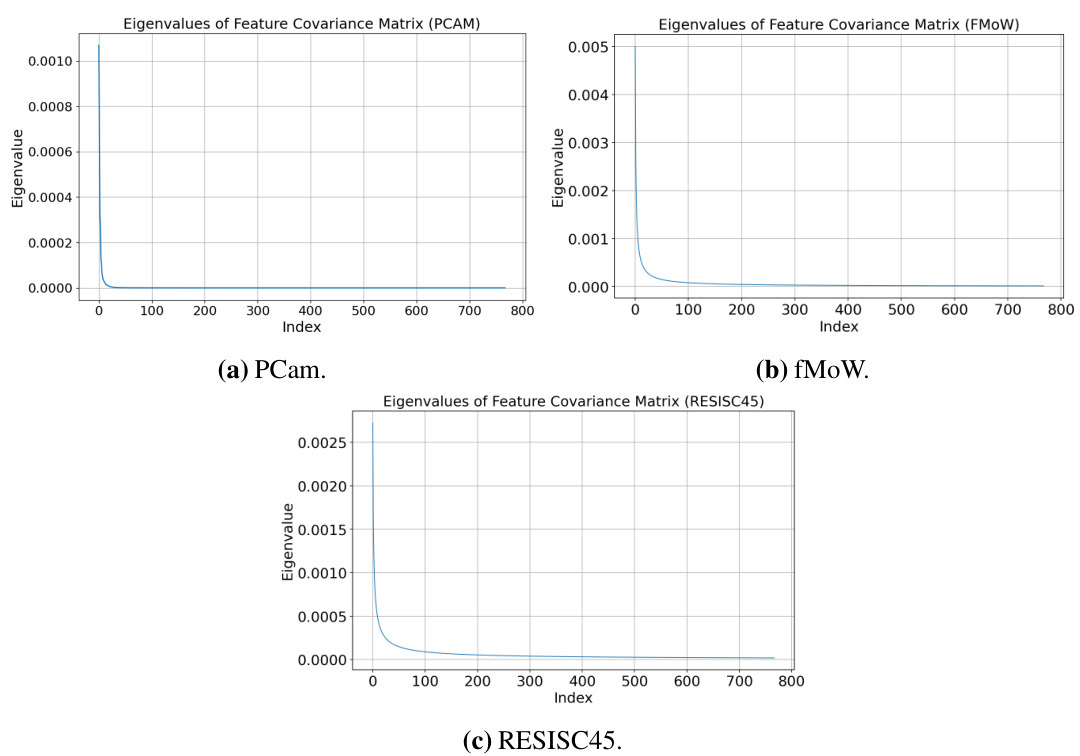
🔼 This figure displays the eigenspectra of feature covariance matrices for three datasets (PCam, fMoW, and RESISC45). Each eigenspectrum shows how much variance in the feature space is explained by each eigenvector. The rapid decay of eigenvalues in all three datasets indicates that the data lies in a low-dimensional subspace, even though these datasets are highly out-of-distribution compared to the CLIP model’s pretraining data. This finding supports the paper’s hypothesis that even with significant distribution shift between public and private data, a shared low-dimensional representation exists, allowing public features to improve private model training.
read the caption
Figure 5: Eigenspectra of feature covariance matrices for features extracted from pretrained CLIP ViT-B/32 model.
Full paper#



















