TL;DR#
In-context learning (ICL), where transformers solve downstream tasks using only the input context, is a remarkable ability. A popular hypothesis is that transformers learn a ‘mesa-optimizer’ during autoregressive (AR) pretraining, acting as an algorithm to solve the task. However, existing studies lack rigorous analysis of this non-convex training dynamics. The relationship between data distribution and the success of mesa-optimization is unclear.
This paper investigates the non-convex dynamics of a simplified one-layer linear causal self-attention model. Under a specific data distribution condition, the authors prove that AR training learns the weight matrix W by performing one step of gradient descent to minimize an ordinary least squares (OLS) problem. This validates the mesa-optimization hypothesis. However, the paper also demonstrates that this mesa-optimizer’s ability is limited and highlights the necessary and sufficient conditions for it to recover the data distribution. These findings provide valuable insights into how and why ICL emerges in transformers.
Key Takeaways#
Why does it matter?#
This paper is crucial because it provides rigorous theoretical analysis of mesa-optimization in autoregressively trained transformers, a phenomenon crucial to understanding in-context learning. The sufficient conditions for mesa-optimization to emerge are identified, shedding light on the limitations and capabilities of this approach, and opening new avenues for research in transformer training and in-context learning.
Visual Insights#
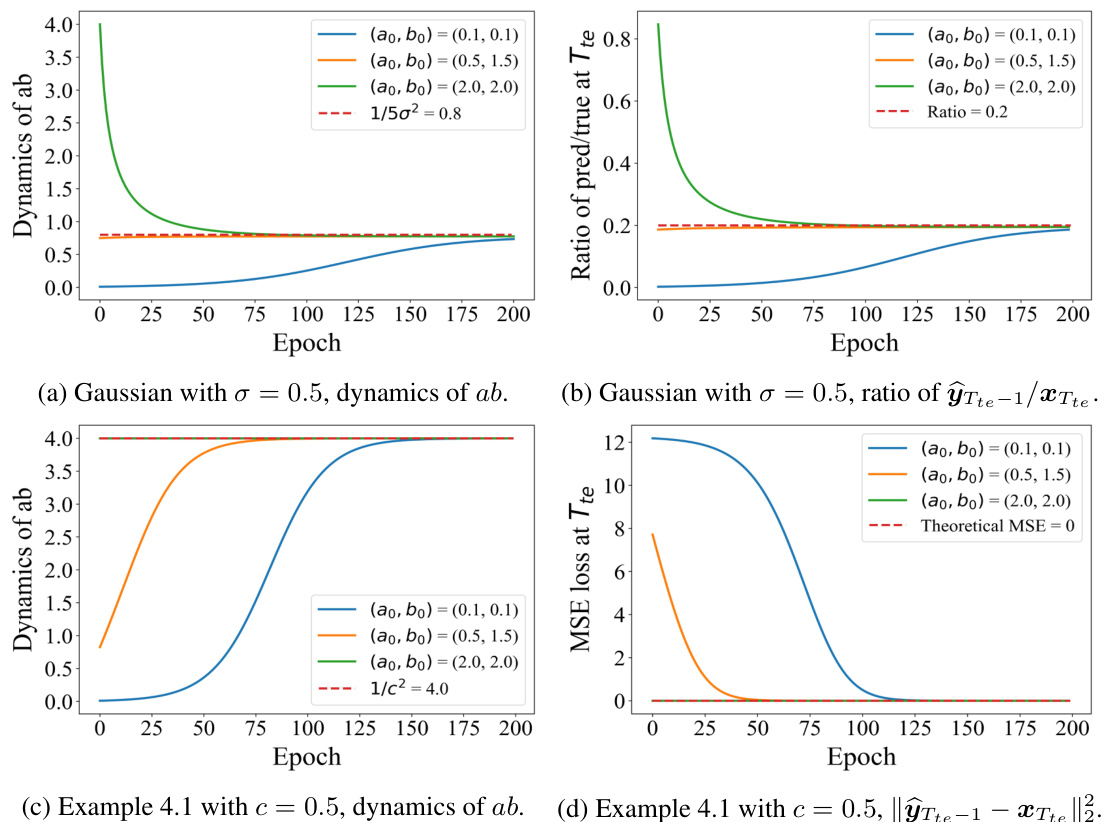
🔼 This figure presents simulation results to verify the theoretical findings of the paper. It demonstrates the convergence behavior of the parameter ‘ab’ under two different initial token distributions: a Gaussian distribution and a distribution as defined in Example 4.1. The plots show that the convergence of ‘ab’ aligns with Theorem 4.1 in both cases. Importantly, it highlights that the model successfully recovers the sequence when using the Example 4.1 initial token but fails to do so when using the Gaussian initial token, thus validating Theorem 4.2 and Proposition 4.1.
read the caption
Figure 1: Simulations results on Gaussian and Example 4.1 show that the convergence of ab satisfies Theorem 4.1. In addition, the trained transformer can recover the sequence with the initial token from Example 4.1, but fails to recover the Gaussian initial token, which verifies Theorem 4.2 and Proposition 4.1, respectively.
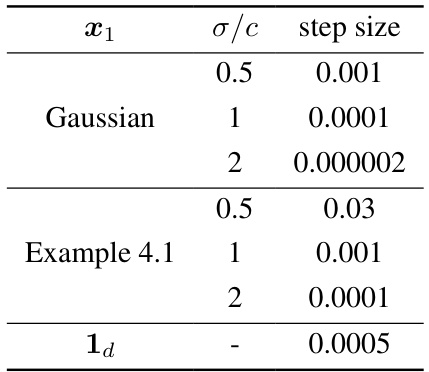
🔼 This table shows the step sizes used for gradient descent in different simulation settings. The simulations varied the initial token distribution (Gaussian with different standard deviations, a sparse distribution from Example 4.1 with different scales, and a fixed all-ones vector). The step size was adjusted to optimize the training process for each setting.
read the caption
Table 1: Step size in different simulations.
In-depth insights#
Mesa-Opt Emergence#
Mesa-optimization, a fascinating concept in the field of AI, proposes that during the autoregressive pretraining of transformers, a meta-optimizer emerges. This meta-optimizer, in essence, is a learned algorithm that guides the transformer’s in-context learning abilities. The paper delves into the conditions under which this mesa-optimizer successfully emerges, exploring the interplay of data distribution and training dynamics. Crucially, it investigates whether the non-convex nature of the training process allows for the convergence to the ideal mesa-optimizer. A key finding is that under specific data distribution assumptions, the transformer learns a mesa-optimizer that performs one step of gradient descent for an OLS problem in-context. This validates the mesa-optimization hypothesis. However, the analysis reveals capability limitations, highlighting that stronger assumptions are needed to recover the data distribution perfectly. The research also extends beyond these ideal conditions to reveal that generally, the trained transformer does not perform vanilla gradient descent for the OLS problem, illustrating the complexity of mesa-optimizer emergence.
AR Training Dynamics#
Autoregressive (AR) training dynamics in transformers are crucial for understanding their in-context learning (ICL) capabilities. The non-convex nature of the loss landscape makes analyzing these dynamics challenging. Research suggests that AR training leads to the emergence of mesa-optimizers, meaning the transformer’s forward pass implicitly performs optimization on the input context to predict the next token. However, whether this optimization process resembles standard gradient descent is still debated. Studies explore simplified linear models to provide theoretical insights, demonstrating that under specific data distribution assumptions, the trained model implements a single step of gradient descent for a least squares problem. The influence of data distribution and model architecture on the convergence of AR training and the quality of the resulting mesa-optimizer remains an open area of investigation. Further work is needed to extend these findings to more complex models and non-ideal conditions, thus providing a more comprehensive understanding of ICL in large language models.
OLS Problem Solved#
The concept of “OLS Problem Solved” within the context of autoregressively trained transformers is a significant finding. It suggests that the forward pass of a trained transformer, particularly under specific data distribution conditions (Assumption 4.1), effectively mirrors one step of gradient descent to solve an ordinary least squares (OLS) regression problem. This is a key theoretical validation of the mesa-optimization hypothesis, which posits that transformers implicitly learn optimization algorithms during pretraining. The study’s contribution lies in demonstrating that this phenomenon isn’t merely a result of specific architectural assumptions, but rather emerges under certain data conditions, significantly advancing our understanding of in-context learning. However, limitations exist, as the mesa-optimizer’s capability to perfectly recover the data distribution is dependent on stricter assumptions (Assumption 4.2), highlighting that the trained model will not always perform a vanilla gradient descent for the OLS problem.
ICL Capability Limits#
The inherent limitations of in-context learning (ICL) are a crucial area of investigation. While ICL allows models to seemingly adapt to new tasks without explicit retraining, its capabilities are bounded. A key limitation is the model’s reliance on patterns and correlations present in the pretraining data. If the downstream task deviates significantly from the distribution seen during pretraining, ICL performance degrades. This highlights the crucial role of data diversity and representativeness in the pretraining phase for broad ICL applicability. Furthermore, the length of the in-context examples plays a vital role. While longer contexts might provide more information, they also increase computational cost and could introduce noise or irrelevant information. The model’s architecture itself poses constraints. Simple models may exhibit limited ICL capabilities compared to more complex architectures that can learn more intricate relationships. Theoretical analysis often relies on simplifying assumptions, making it challenging to fully grasp the dynamics of ICL in real-world scenarios. Therefore, further research should focus on relaxing these assumptions to better understand and improve ICL capabilities.
Future Research#
Future research directions stemming from this paper on mesa-optimization in autoregressively trained transformers could fruitfully explore several avenues. Extending the theoretical analysis beyond the one-layer linear model is crucial to determine the generality of the findings. Investigating multi-layer transformers and incorporating the softmax function, which are more realistic representations of actual models, will enhance the understanding of mesa-optimization in realistic scenarios. Exploring the impact of different data distributions on the emergence of mesa-optimizers is another significant direction. The current study focuses on specific data distributions; broadening the investigation to include more realistic data conditions, including those with noise and dependencies, will enrich our understanding of the phenomenon. The relationship between mesa-optimization and other interpretations of in-context learning (ICL) warrants further investigation. The paper highlights the distinct nature of AR pretraining ICL from few-shot learning; this requires further exploration. Finally, empirical studies on diverse downstream tasks are needed to verify the theoretical results and broaden the impact of these insights on practical applications. Investigating the efficacy of mesa-optimization in various scenarios, such as question answering and text generation, could contribute significantly to advancing the field of transformer-based models.
More visual insights#
More on figures

🔼 This figure presents simulation results that validate the theoretical findings of the paper. The plots show the dynamics of the product ‘ab’ (a parameter related to the trained transformer’s learning process) during the training process for different initial conditions. The results for two scenarios are depicted: 1. Gaussian Initial Token: The initial token is sampled from a Gaussian distribution. This demonstrates the convergence behavior according to Theorem 4.1 and illustrates the limitations described in Proposition 4.1 showing that the trained model fails to learn the true distribution. 2. Sparse Initial Token (Example 4.1): The initial token is sampled from a distribution defined in Example 4.1 in the paper. This condition leads to the convergence to the true distribution, highlighting a sufficient condition for mesa-optimization to emerge successfully.
read the caption
Figure 1: Simulations results on Gaussian and Example 4.1 show that the convergence of ab satisfies Theorem 4.1. In addition, the trained transformer can recover the sequence with the initial token from Example 4.1, but fails to recover the Gaussian initial token, which verifies Theorem 4.2 and Proposition 4.1, respectively.
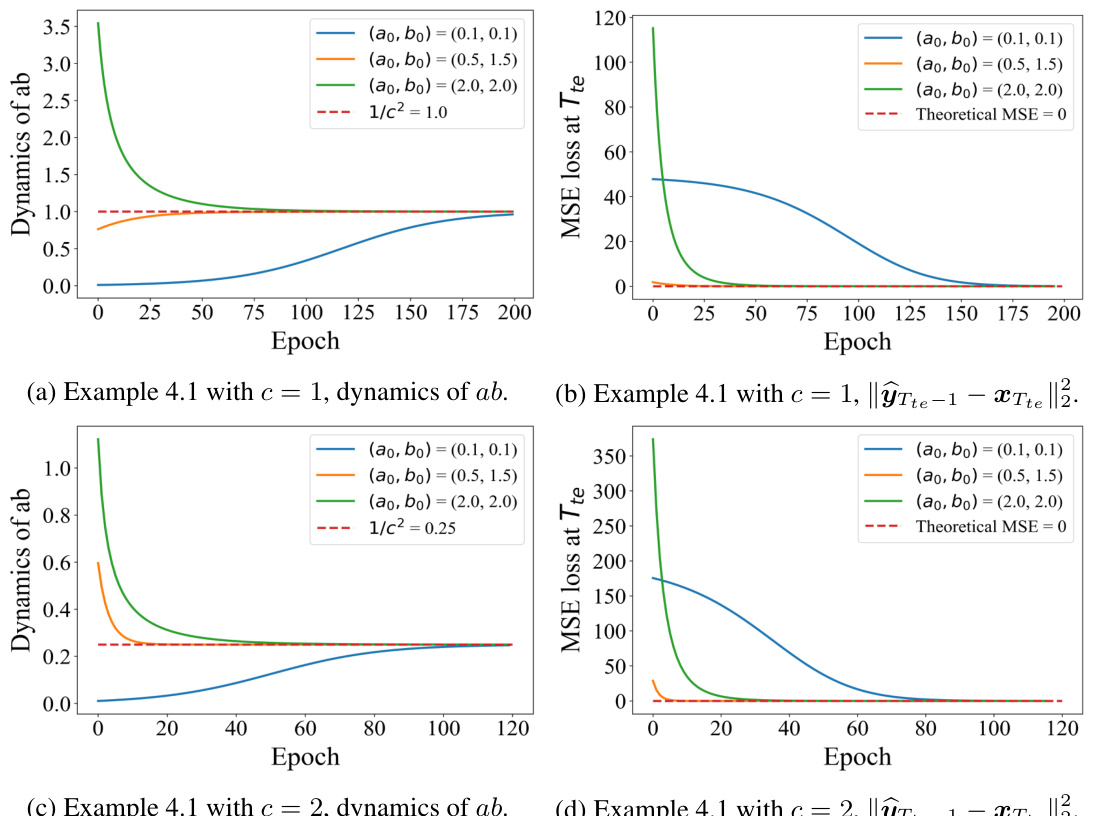
🔼 This figure presents simulation results that validate the theoretical findings of the paper. The plots show the convergence of the product ‘ab’ (a parameter from the linear transformer model) under different initializations and data distributions. The key observation is that the model’s performance is dependent on the data distribution, specifically verifying Theorem 4.1, 4.2 and Proposition 4.1 which describe when and how well the transformer learns to minimize an OLS problem.
read the caption
Figure 1: Simulations results on Gaussian and Example 4.1 show that the convergence of ab satisfies Theorem 4.1. In addition, the trained transformer can recover the sequence with the initial token from Example 4.1, but fails to recover the Gaussian initial token, which verifies Theorem 4.2 and Proposition 4.1, respectively.
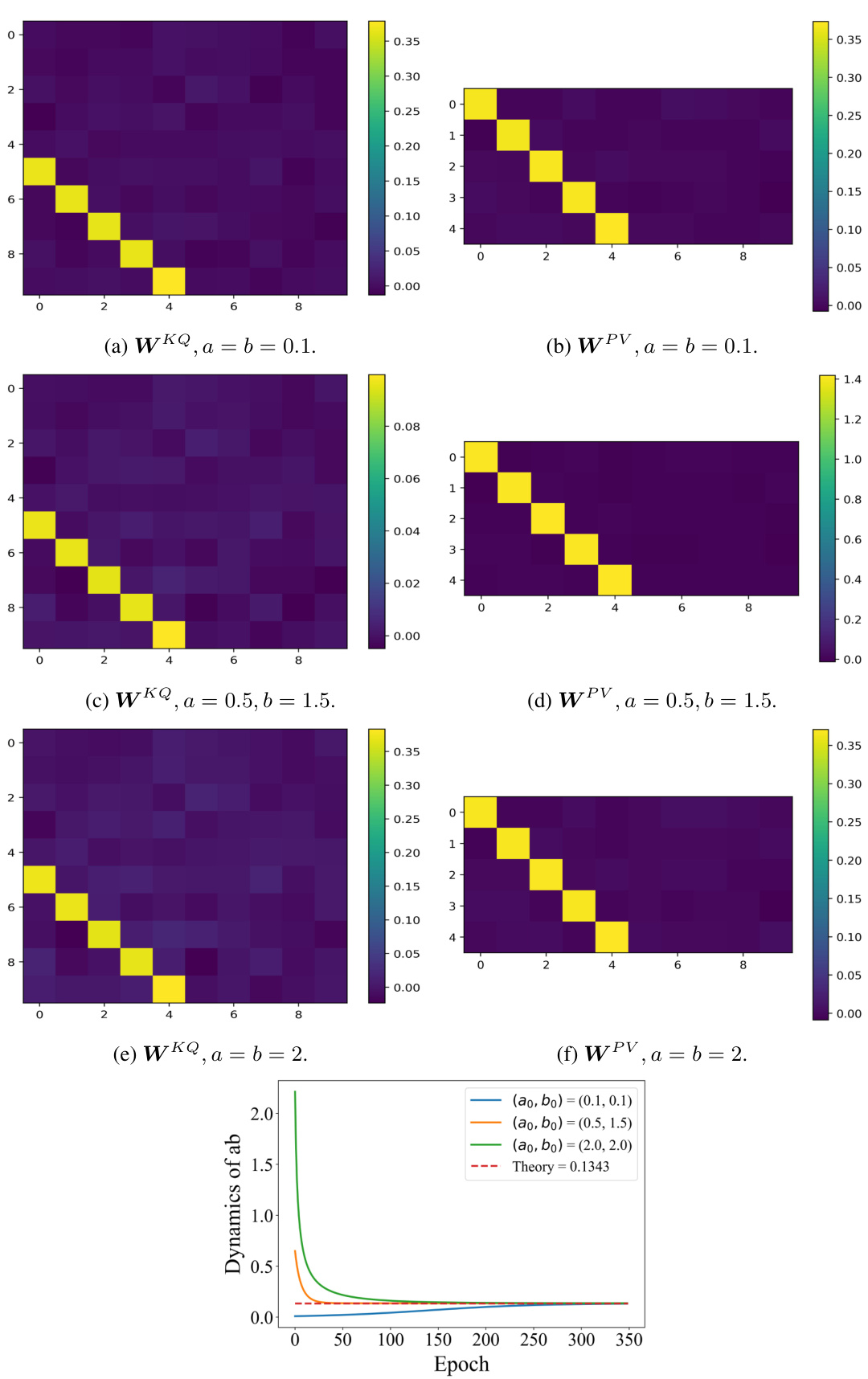
🔼 This figure displays heatmaps of the matrices WKQ and WPV obtained after training a one-layer linear transformer with a full-one initial token. Different diagonal initializations (ao, bo) were used: (0.1, 0.1), (0.5, 1.5), and (2, 2). The heatmaps visualize the values of the matrices, highlighting the diagonal structure emphasized by the diagonal initialization strategy (Assumption 3.1). The highlighted (red) blocks in the matrices are those relevant to the next-token prediction task (ŷt). The dynamics of ab (the product of diagonal elements of WPV and WKQ) over the epochs are also presented, showing its convergence to a certain value based on the specific initialization.
read the caption
Figure 7: WKQ and WPV of full-one start points with different diagonal initialization. The read blocks in Assumption 3.1 are presented, which are related to the final prediction.
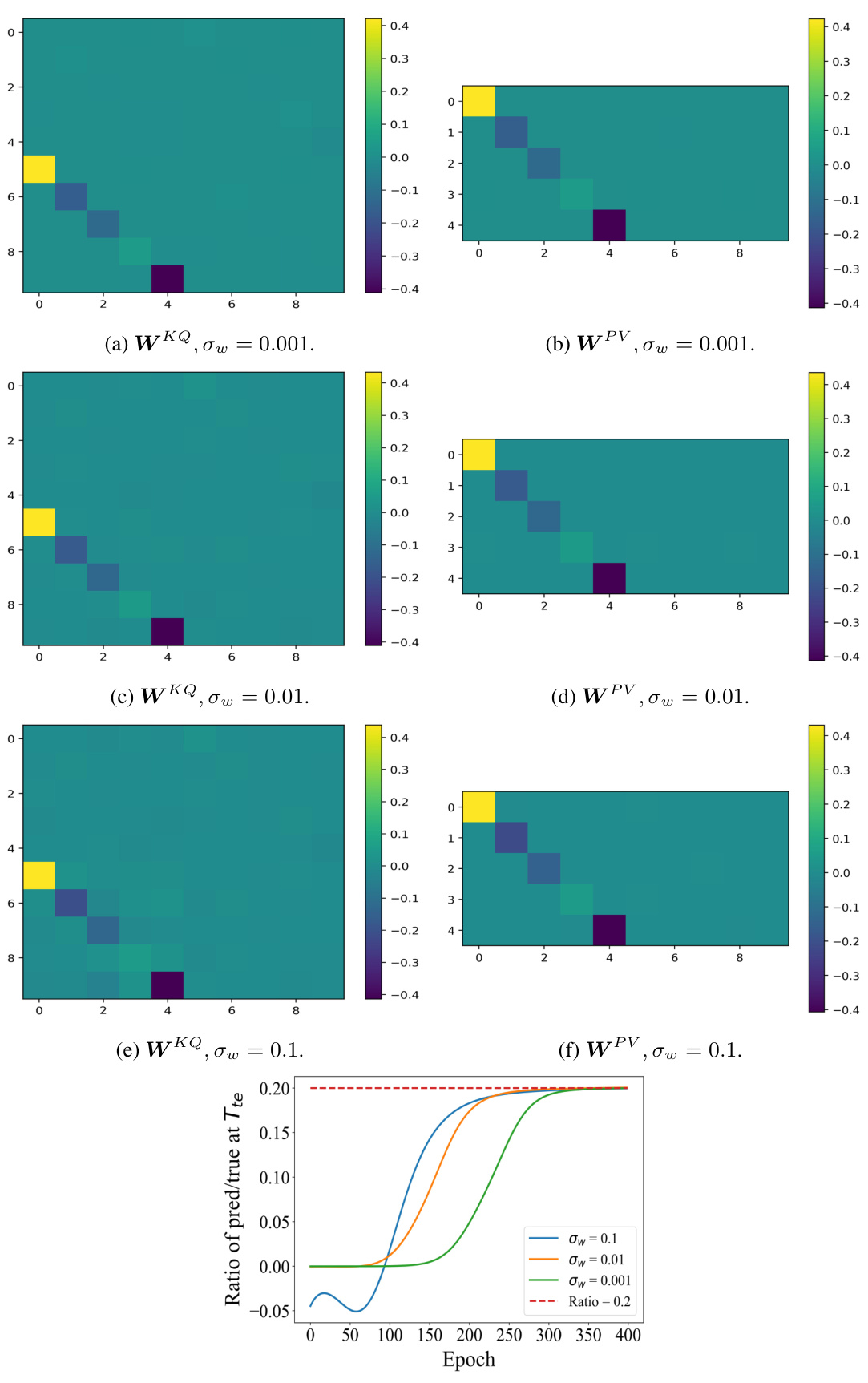
🔼 This figure displays simulation results that verify the theoretical findings of the paper. It demonstrates the convergence behavior of the parameters (WKQ and WPV) under different variance (σω) of Gaussian initialization. The results show that even with varied Gaussian initialization, the key parameters maintain a strong diagonal structure, aligning with the theoretical prediction. This suggests robustness to the initialization method and the convergence to the mesa-optimizer hypothesis.
read the caption
Figure 5: Results of Gaussian start point (σ = 1) and standard Gaussian initialization with different variance σω. The read blocks in Assumption 3.1 are presented, which are related to the final prediction. The parameter matrices retain the same strong diagonal structure and test performance as those of the diagonal initialization.
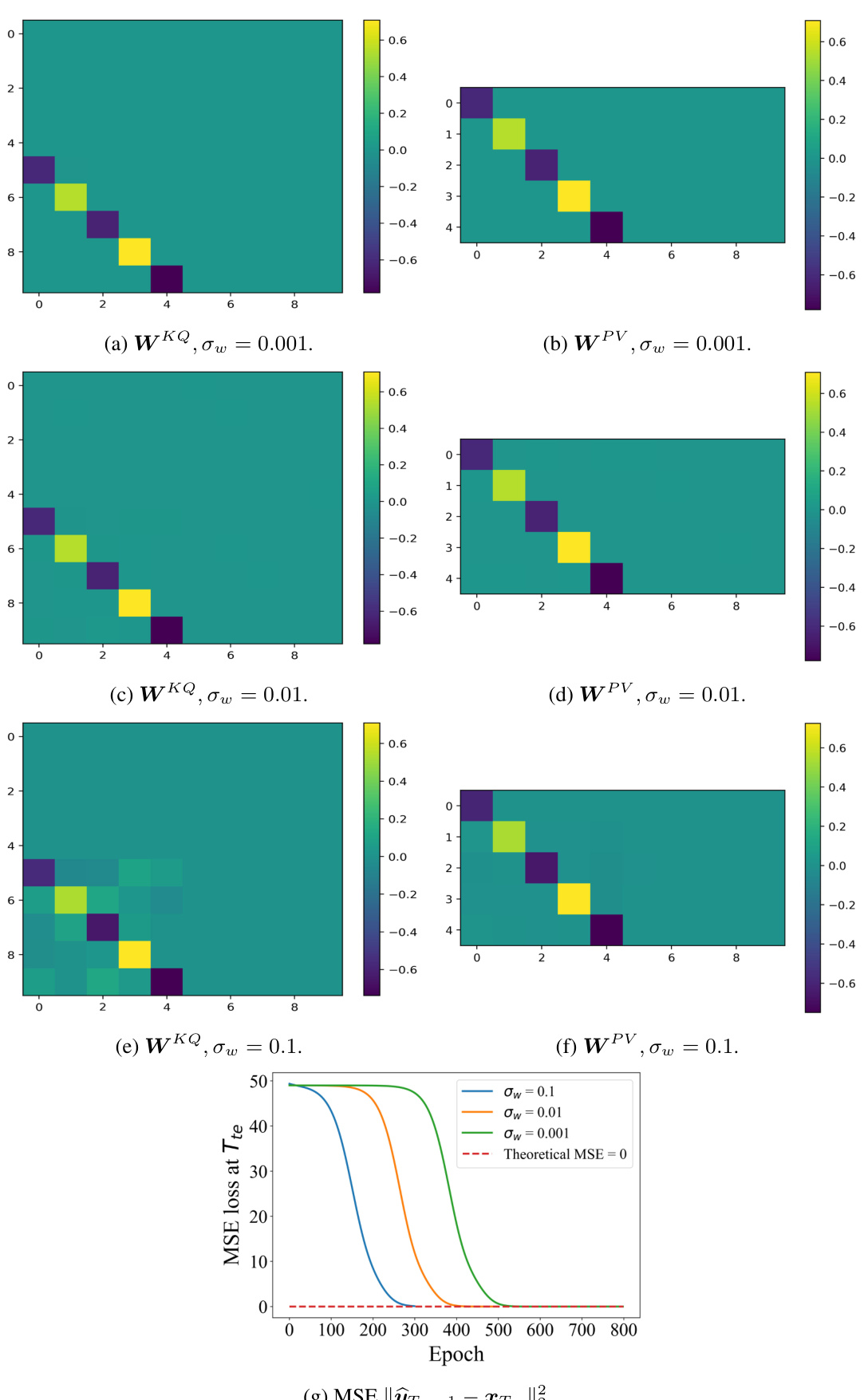
🔼 This figure visualizes the results of experiments using Gaussian start points (σ = 1) with standard Gaussian initialization, but varying the variance (σω). It shows the learned matrices WKQ and WPV for different values of σω. The key observation is that despite the change in variance, the resulting matrices maintain a strong diagonal structure, similar to the results obtained with diagonal initialization. This supports the paper’s claim that the diagonal structure is a significant factor in the model’s behavior and that this behavior is relatively robust to changes in the initialization.
read the caption
Figure 5: Results of Gaussian start point (σ = 1) and standard Gaussian initialization with different variances σω. The read blocks in Assumption 3.1 are presented, which are related to the final prediction. The parameter matrices retain the same strong diagonal structure and test performance as those of the diagonal initialization.
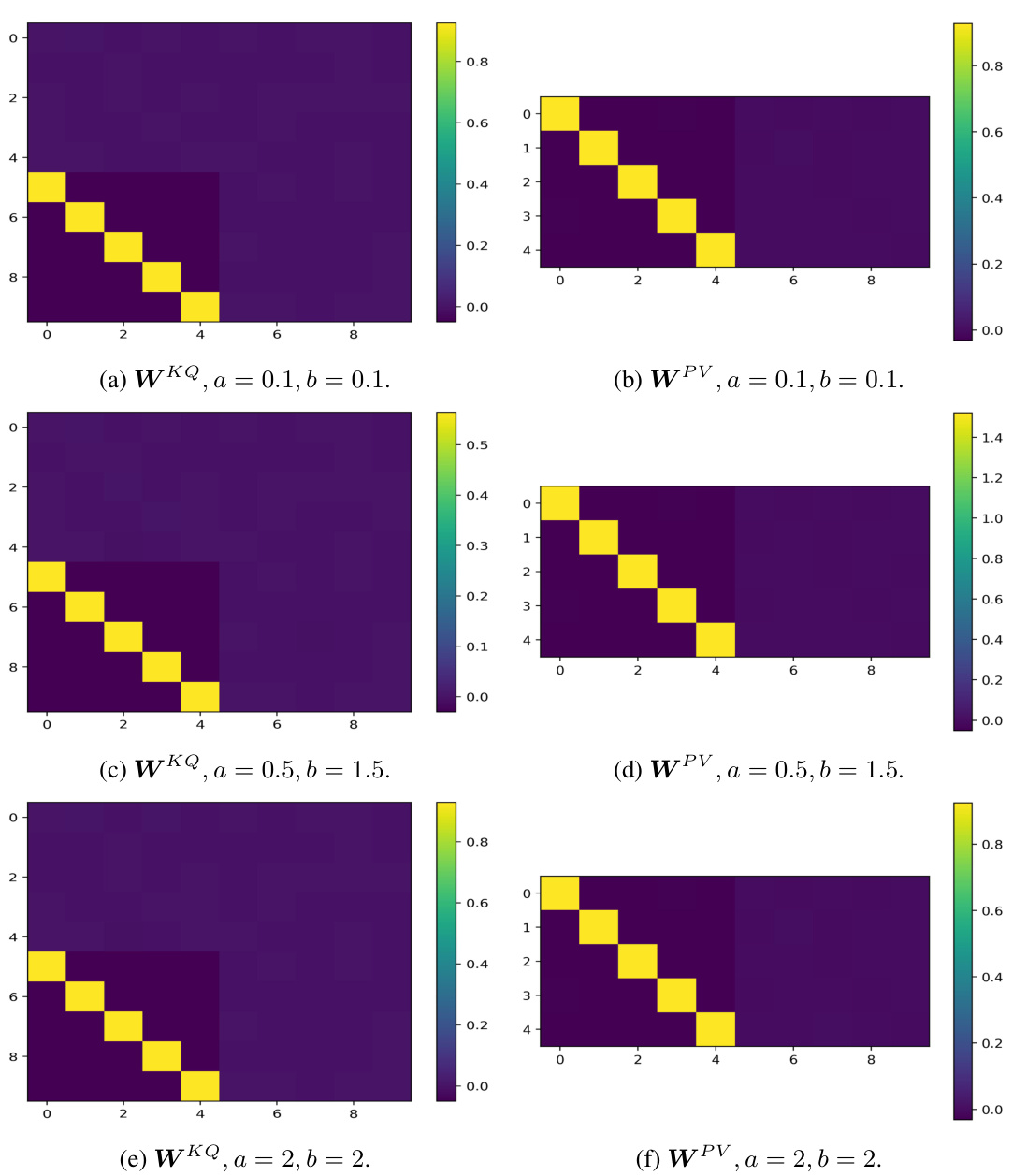
🔼 This figure visualizes the learned weight matrices WKQ and WPV of a one-layer linear transformer with a full-one initial token under different diagonal initializations. The color intensity in the heatmap represents the magnitude of the weights. The red blocks highlight the parameters that are directly related to the next-token prediction, as specified in Assumption 3.1 of the paper. The figure demonstrates how the weight matrices evolve during training with different starting points, providing insights into the impact of initialization on model learning. The patterns in the matrices can be related to the overall mesa-optimization behavior discussed in the paper.
read the caption
Figure 7: WKQ and WPV of full-one start points with different diagonal initialization. The red blocks in Assumption 3.1 are presented, which are related to the final prediction.
Full paper#



















