TL;DR#
Conformal prediction (CP) is a valuable tool for reliable uncertainty quantification, but existing methods often suffer from inefficiently long prediction sets, hindering practical applicability. Moreover, achieving conditional validity, where uncertainty quantification is accurate across different data subpopulations, remains a challenge. This paper tackles these issues.
The proposed method, called Conformal Prediction with Length-Optimization (CPL), offers a novel framework addressing both conditional validity and length efficiency simultaneously. CPL constructs prediction sets with near-optimal length, while ensuring conditional validity under various covariate shifts including marginal and group-conditional coverage. The framework leverages strong duality results to prove optimality and provides practical algorithms for finite-sample scenarios.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses a critical limitation in conformal prediction, offering a new framework for constructing shorter, more informative prediction sets while maintaining accuracy. This is relevant to various fields that rely on reliable uncertainty quantification, opening avenues for improved decision-making in applications ranging from healthcare to robotics.
Visual Insights#
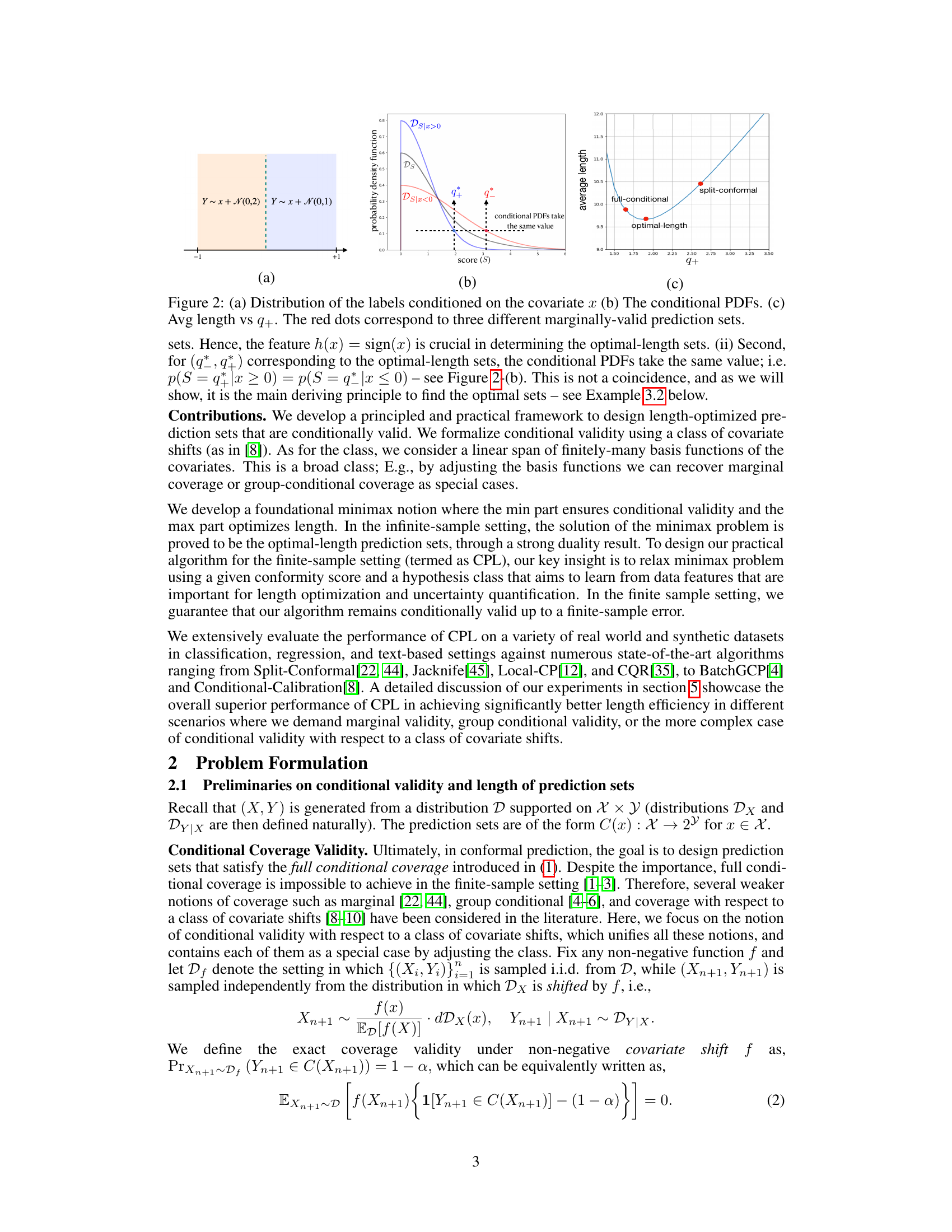
🔼 The CP pipeline consists of three stages: 1) Training a model using training data. 2) Designing a conformity score. 3) Constructing prediction sets. This figure shows that the authors’ framework operates at the third stage, aiming to design prediction sets that are both conditionally valid and length-efficient (i.e., as small as possible while maintaining validity), given a predictive model and a conformity score. Previous work focused on improving the first two stages, leaving length optimization at the final stage largely unaddressed.
read the caption
Figure 1: The CP pipeline.

🔼 This table presents the results of the first part of the experiment, which focuses on methods applicable to black-box predictors and generic conformity scores. The table compares the average length and coverage of prediction sets generated by different methods: Split Conformal, Jackknife, Local Split Conformal, LocalCP, and CPL. The results show the average performance over 100 random splits of multiple regression datasets.
read the caption
Table 1: First part
In-depth insights#
Conditional Validity#
The concept of ‘Conditional Validity’ in conformal prediction addresses the crucial limitation of standard marginal coverage. Marginal coverage, while ensuring that prediction sets include the true label with a specified probability overall, fails to guarantee accuracy across different subpopulations of the data. Conditional validity aims to rectify this by providing coverage guarantees for specific subgroups, such as different age groups in a medical study or various customer segments in marketing. This is particularly important when dealing with covariate shift, i.e. differences in the distribution of data used for training versus testing. The paper explores different notions of conditional validity, ranging from group-conditional coverage (guaranteeing validity within pre-defined groups) to a more general definition using a class of covariate shifts. Achieving full conditional validity is generally impossible with finite data, so the focus is on constructing valid prediction sets under more relaxed yet meaningful assumptions. The framework developed in this paper provides a principled approach to handle these issues and construct efficient, conditionally valid prediction sets. The methods are evaluated empirically against diverse real-world and synthetic datasets, demonstrating improved performance in terms of prediction set size while maintaining the desired conditional coverage levels.
Length Optimization#
The concept of ‘Length Optimization’ in the context of conformal prediction is crucial for practical applicability. The core idea revolves around minimizing the size of prediction sets while maintaining validity. The paper highlights that existing methods often produce unnecessarily large prediction sets, hindering their usefulness. A principled framework is proposed to address this issue by explicitly incorporating length optimization into the construction of prediction sets. This involves a minimax formulation where conditional validity is guaranteed while simultaneously aiming for minimal length. The framework provides theoretical guarantees in the infinite sample regime and demonstrates superior empirical performance compared to state-of-the-art methods across diverse datasets and tasks. The key insight is the use of the covariate information to tailor the prediction set size to specific subpopulations, thereby maximizing efficiency while satisfying conditional validity requirements. The practical implementation is carefully explained, and a comprehensive evaluation showcases the significant improvements achievable through length optimization.
Minimax Formulation#
The minimax formulation section of this research paper presents a novel and principled approach to length optimization in conformal prediction. The core idea is to frame the problem as a minimax optimization: minimizing the average prediction set length while simultaneously maximizing a worst-case coverage guarantee over a specified class of covariate shifts. This elegantly unifies the often-conflicting goals of length efficiency and conditional validity. The authors develop a strong duality result, showing the equivalence between the minimax problem and a more directly solvable primal problem under certain conditions. This duality is crucial, as it provides a theoretical underpinning for their proposed algorithm. While the infinite-sample setting is theoretically elegant, the authors’ key contribution lies in extending the minimax formulation to a finite-sample regime, using structured prediction sets and approximating the outer maximization, thus making it tractable and practical. The paper highlights the theoretical connections to level-set estimation, and the resulting algorithm offers a promising approach to more concise uncertainty quantification.
Finite Sample CPL#
The heading ‘Finite Sample CPL’ anticipates a discussion on the practical application of the Conformal Prediction with Length Optimization (CPL) framework. While the infinite sample regime provides theoretical guarantees of conditional validity and length optimality, the finite sample setting reflects real-world constraints. This section would delve into the algorithmic implementation of CPL, addressing challenges such as finite sample bias, the selection of appropriate regularization techniques, and the choice of a suitable hypothesis class for approximating the optimal prediction sets. A key focus would be on the empirical performance of the algorithm, showcasing its conditional validity and length efficiency (relative to benchmarks) across various datasets and problem settings. Finite sample error bounds or confidence intervals could also be presented to quantify the accuracy and reliability of the prediction sets generated. The discussion would connect theoretical results to practical considerations, demonstrating the effectiveness of CPL in handling real-world data and computational limits.
Empirical Results#
The empirical results section of a research paper is crucial for validating the claims made in the theoretical sections. A strong empirical results section would demonstrate the effectiveness of the proposed method across multiple datasets and various experimental settings. It would compare the new approach against relevant baselines, highlighting its strengths, such as superior accuracy, greater efficiency, or robustness to noise or distributional shifts. The results should be presented clearly and concisely, usually with tables and figures, and statistical significance should be explicitly stated. Ideally, the section would also include an in-depth analysis of the results, exploring potential limitations and edge cases, and offering insights that go beyond simple performance comparisons. Robustness analysis evaluating behavior under various hyperparameter choices or data conditions would further strengthen the findings. Overall, the goal is to present a convincing and comprehensive case for the proposed methodology’s efficacy by using rigorously collected and carefully analyzed data, while acknowledging any limitations or areas for future research.
More visual insights#
More on figures
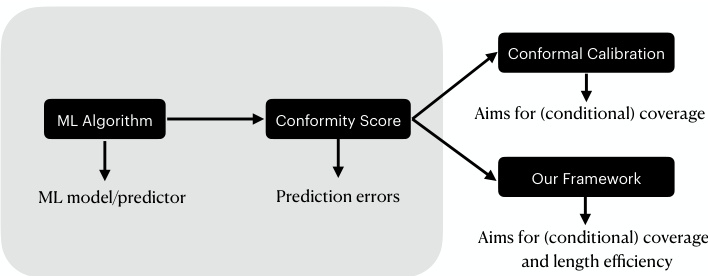
🔼 This figure illustrates three key aspects of the toy example used to explain the principles and challenges of length optimization in conformal prediction. (a) Shows the distribution of labels Y conditioned on the covariate X, highlighting the different variances for x < 0 and x ≥ 0. (b) Displays the conditional probability density functions (PDFs) of the conformity score S given X, demonstrating how the distributions differ based on the value of X. Finally, (c) plots the average length of prediction sets against the parameter q+, demonstrating the existence of an optimal length solution that is distinct from those constructed by split-conformal methods.
read the caption
Figure 2: (a) Distribution of the labels conditioned on the covariate x (b) The conditional PDFs. (c) Avg length vs q+. The red dots correspond to three different marginally-valid prediction sets.
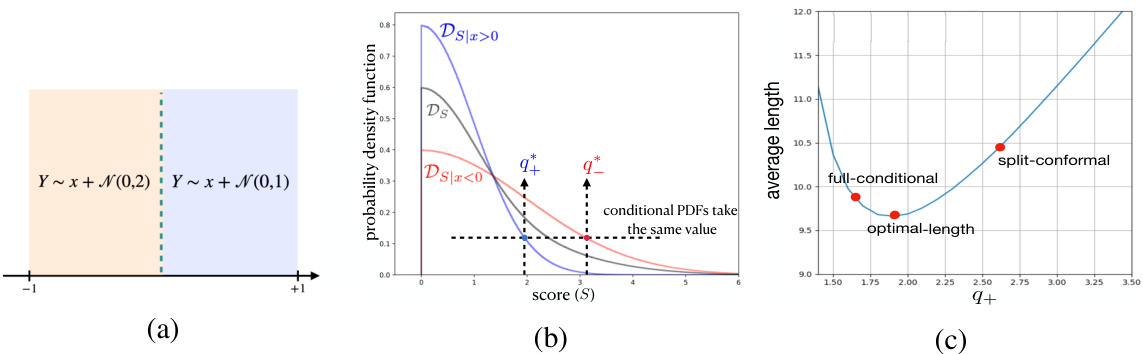
🔼 This figure presents the results of applying CPL and Split Conformal to multiple-choice question answering datasets. The left plot shows the coverage achieved by each method on each dataset (BigBench, MMLU, OpenBookQA, PIQA, TruthfulQA), with a horizontal dashed line indicating the target coverage of 90%. The right plot displays the mean prediction set sizes for each method and dataset. The error bars represent the standard deviation across multiple trials. The figure visually demonstrates that CPL achieves comparable coverage to Split Conformal but with significantly smaller prediction set sizes, indicating superior length efficiency.
read the caption
Figure 3: Left-hand-side plot shows coverage and right-hand-side shows mean prediction set size.

🔼 This figure compares the performance of CPL, Split Conformal, BatchGCP, and an Optimal Oracle baseline on a synthetic regression task with group-conditional coverage requirements. The left panel shows the coverage achieved by each method in 20 different groups, while the right panel shows the average length of the prediction intervals generated by each method. The results indicate that CPL achieves near-optimal length while maintaining the desired coverage level across all groups, unlike other methods.
read the caption
Figure 4: Left-hand-side plot shows coverage and right-hand-side shows mean interval length.

🔼 This figure compares the performance of CPL, Split Conformal in terms of coverage and prediction set size for multiple choice question answering task. The left plot displays the coverage achieved by each method across various datasets (BigBench, MMLU, OpenBookQA, PIQA, TruthfulQA), showing that CPL maintains a coverage close to 90%, similar to Split Conformal. The right plot presents the mean prediction set size for each method, revealing that CPL consistently produces smaller prediction sets than Split Conformal across all datasets, indicating improved length efficiency.
read the caption
Figure 3: Left-hand-side plot shows coverage and right-hand-side shows mean prediction set size.
More on tables

🔼 This table presents the results of the first part of the experiment, comparing different methods for achieving marginal coverage in regression tasks. The methods compared include Split Conformal, Jackknife, Local Split Conformal, LocalCP, and CPL. For each method, the average length of the prediction sets and the average coverage achieved are reported. The experiment was run on 11 real-world regression datasets (listed in Appendix J) using 100 random train/calibration/test data splits.
read the caption
Table 1: First part
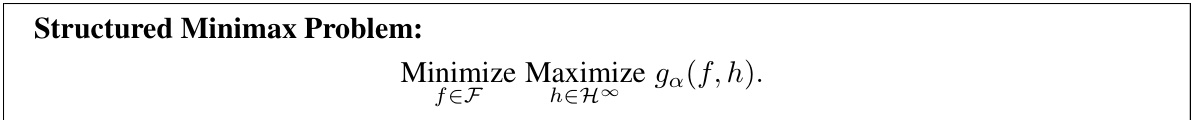
🔼 This table shows the results of applying different methods for achieving marginal coverage validity for regression datasets. The methods are compared based on their average length and coverage rate. The methods include standard and locally adaptive split conformal methods, as well as conformalized quantile regression and the proposed CPL method. The results are averages over 100 random dataset splits, with standard deviations below 1%.
read the caption
Table 1: First part
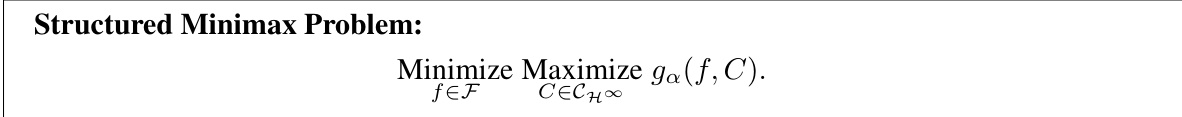
🔼 This table presents the results of the first part of the experiment in Section 5.1, comparing various methods for constructing prediction sets with marginal coverage. The methods compared include Split Conformal, Jackknife, Local Split Conformal, LocalCP, and the proposed CPL method. The table shows the average length of the prediction sets and the coverage achieved by each method across multiple datasets. The results demonstrate the potential of CPL to achieve shorter prediction sets while maintaining the desired marginal coverage.
read the caption
Table 1: First part

🔼 This table shows the length and coverage achieved by different methods for marginal coverage in regression tasks using generic conformity scores. The methods compared include Split Conformal, Jackknife, Local Split Conformal, LocalCP, and CPL. The results highlight CPL’s ability to achieve comparable coverage with shorter prediction set lengths.
read the caption
Table 1: First part

🔼 This table presents the results of the first part of the experiment section (Part I: Marginal Coverage for Multiple Choice Question Answering) in the paper. The table compares different methods for constructing prediction sets in multiple-choice question answering tasks. The methods being compared are Split Conformal, Jackknife, Local-SC, LocalCP, and the proposed CPL method. For each method, the average length of the prediction sets and the coverage are reported. The results show that CPL achieves similar coverage to other methods while producing significantly shorter prediction sets.
read the caption
Table 1: First part
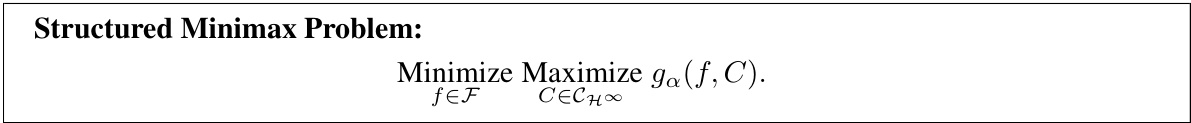
🔼 This table presents the results of the first part of the experiment comparing different methods for achieving marginal coverage in regression tasks. The methods compared include Split Conformal, Jackknife, Local Split Conformal, LocalCP, and CPL. The table shows the average length of prediction sets produced by each method and the corresponding average coverage achieved. The results are averages over 100 random splits of the datasets.
read the caption
Table 1: First part
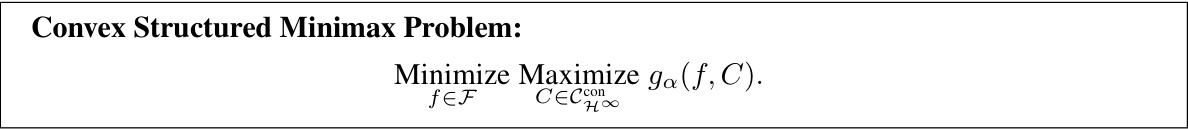
🔼 This table presents the results of the first part of the experiment in Section 5.1, comparing different methods for achieving marginal coverage in regression tasks using generic conformity scores. The table shows the average length of prediction sets and the coverage achieved by each method across 11 datasets. The methods compared are Split Conformal, Jackknife, Local Split Conformal, LocalCP, and CPL. The table demonstrates that the proposed method, CPL, achieves comparable coverage to other methods while producing smaller prediction sets.
read the caption
Table 1: First part

🔼 This table presents the results of the first part of the experiment, comparing different methods for achieving marginal coverage in regression tasks. It shows the average length and coverage achieved by various methods, including Split Conformal, Jackknife, Local Split Conformal, LocalCP, and CPL. The goal is to show how CPL performs in comparison to other state-of-the-art approaches in a practical setting. Smaller length values are better.
read the caption
Table 1: First part
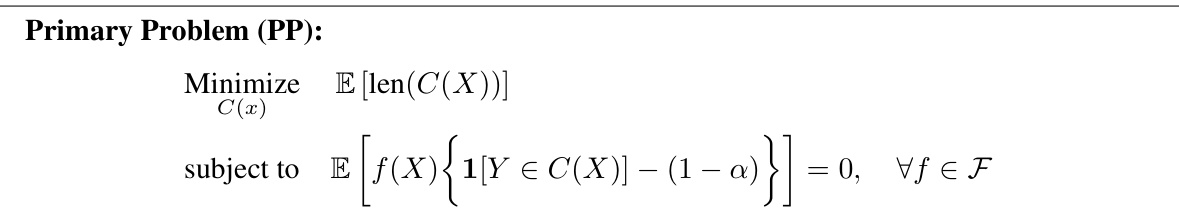
🔼 The table presents the results of the first part of the experiment in Section 5.2, comparing the length and coverage of different methods for achieving marginal coverage in regression tasks. The methods compared include Split Conformal, Jackknife, Local-SC, LocalCP, and CPL, using a generic neural network-based conformity score. The table shows that CPL achieves comparable coverage to other methods while having a shorter prediction set length (smaller size).
read the caption
Table 1: First part

🔼 This table presents the results of the first part of the experiment comparing different methods for achieving marginal coverage in regression tasks. It shows the average length of the prediction sets and the coverage achieved by each method: Split Conformal, Jackknife, Local-SC, LocalCP, and CPL. The methods are evaluated using a generic conformity score based on a neural network.
read the caption
Table 1: First part
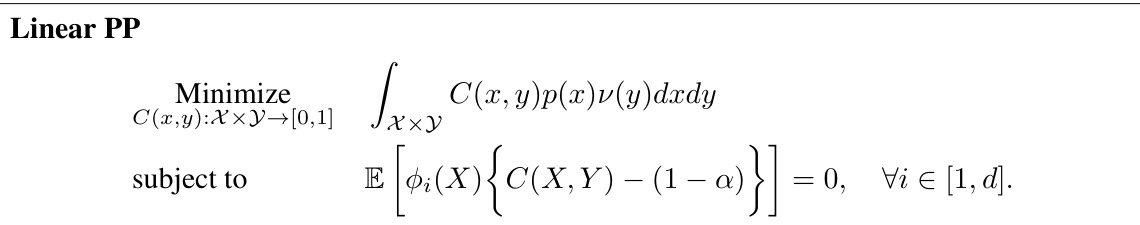
🔼 This table presents the results of the first part of the experiment, comparing different methods for constructing prediction sets in regression tasks. The methods compared are: Split Conformal, Jackknife, Local-SC, LocalCP, and CPL. For each method, the average length of prediction sets and the corresponding coverage are reported. The goal is to evaluate the efficiency of constructing prediction sets with marginal coverage validity.
read the caption
Table 1: First part
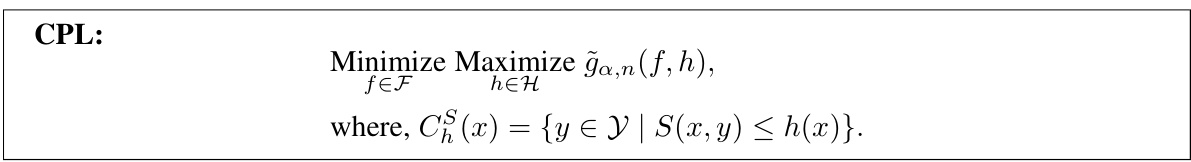
🔼 This table presents the results of the first part of the experiment, comparing different methods for achieving marginal coverage in regression tasks. The methods compared include Split Conformal, Jackknife, Local Split Conformal, LocalCP, and CPL. The table shows the average length of the prediction sets and the coverage achieved by each method. The results demonstrate the ability of CPL to achieve comparable coverage to other methods while maintaining a shorter prediction set length.
read the caption
Table 1: First part

🔼 This table presents the results of the first part of the experiment section in the paper, which focuses on methods applicable to black-box predictors and conformity scores. It compares the performance of different methods (Split Conformal, Jacknife, Local-SC, LocalCP, and CPL) in terms of average length and coverage for multiple choice question answering. The conformity score used was S(x,y) = |y-f(x)|, where f is a neural network trained on a training set. CPL achieves the shortest prediction set length while maintaining high coverage.
read the caption
Table 1: First part
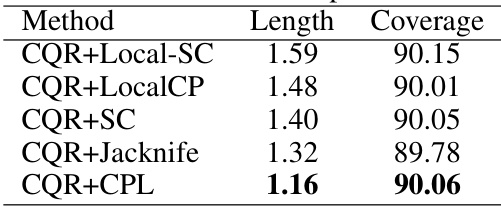
🔼 This table presents the results of applying various conformal prediction methods combined with CQR (Conformalized Quantile Regression) on 11 real-world regression datasets. The methods compared include CQR combined with Local-SC, LocalCP, SC, Jacknife, and CPL (Conformal Prediction with Length Optimization). The table shows the average length of the prediction sets and the achieved coverage for each method, obtained over 100 random data splits. CPL demonstrates the shortest average prediction interval length while maintaining the desired coverage rate.
read the caption
Table 2: Second part

🔼 This table compares the performance of four different combinations of training methods (ERM and Conformal Training) and calibration methods (Split Conformal and CPL) on the CIFAR-10 dataset. The metrics reported are coverage, average prediction set length, and the training/calibration/test data splits used for each configuration. The base accuracy is the accuracy of the base model before calibration.
read the caption
Table 3: Comparison of different training and calibration methods
Full paper#