TL;DR#
Traditional performative prediction methods often rely on accurate modeling of how machine learning models alter data distributions (distribution maps). However, these maps are frequently misspecified in real-world scenarios, leading to suboptimal performance. This paper tackles this crucial limitation.
The paper proposes a novel framework called “distributionally robust performative prediction” that uses robust optimization techniques. It introduces a new solution concept—DRPO (distributionally robust performative optimum)—that guarantees robust performance even when distribution maps are misspecified. The authors also demonstrate the method’s efficiency via reformulation and present empirical results showing DRPO’s advantages over traditional methods.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on performative prediction and robust optimization. It addresses a critical limitation of existing methods by enhancing their robustness against misspecified distribution maps, which is a common issue in real-world applications. The proposed framework and theoretical guarantees provide a new avenue for developing more reliable and robust predictive models. Its focus on worst-case performance and efficient optimization techniques is highly relevant to the current trend of building more robust and trustworthy AI systems. The findings are particularly valuable for domains like finance and education where models influence the data they predict.
Visual Insights#
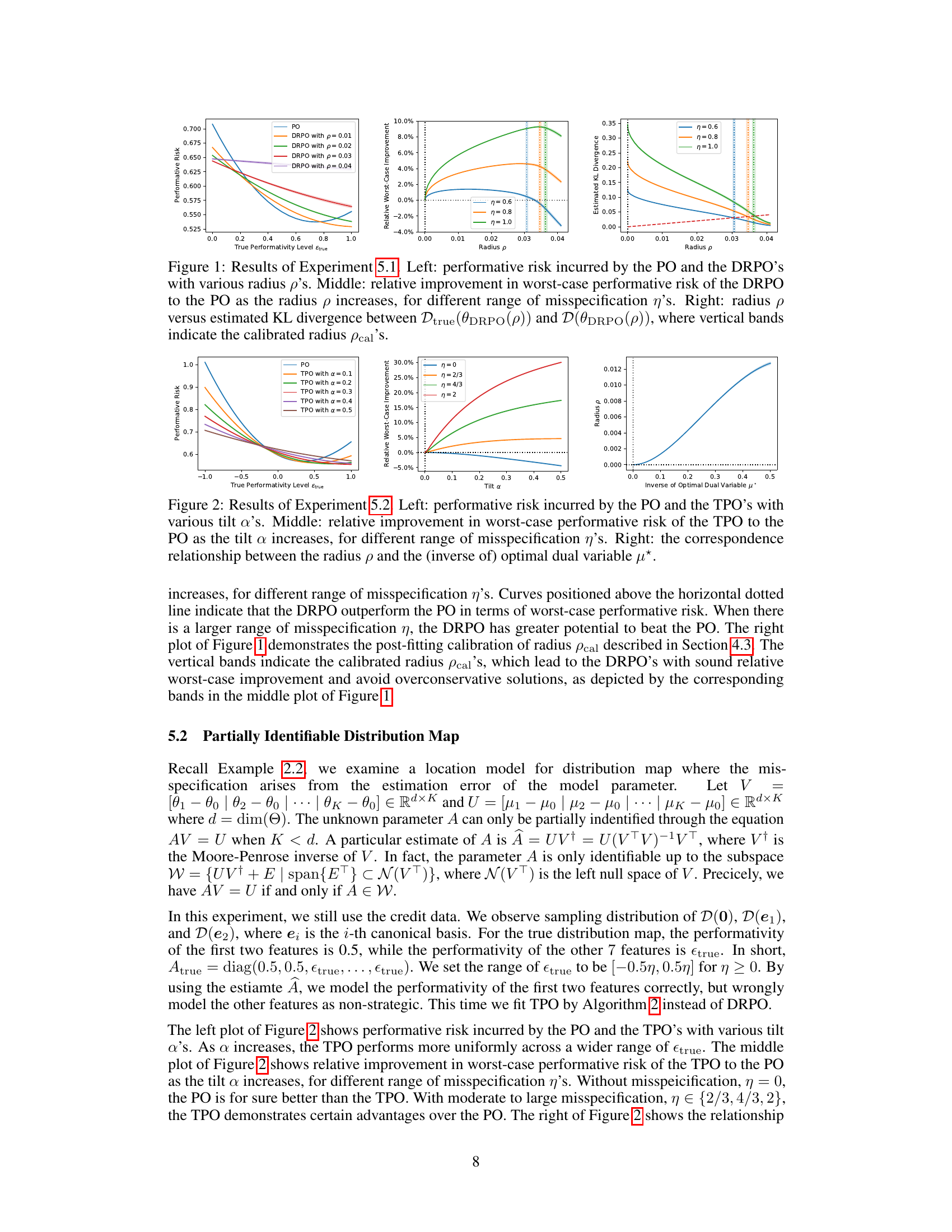
🔼 This figure shows the results of Experiment 5.1, which investigates strategic classification with a misspecified cost function. The left panel displays the performative risk for the PO (standard performative prediction) and several DRPO models (distributionally robust performative prediction) with different values of the radius ‘p’. The middle panel illustrates the relative improvement in worst-case performative risk achieved by the DRPO compared to the PO across a range of misspecification levels (η). Finally, the right panel shows the relationship between the radius ‘p’ and the estimated KL divergence between the true and nominal distribution maps, with vertical lines indicating the calibrated radius.
read the caption
Figure 1: Results of Experiment 5.1. Left: performative risk incurred by the PO and the DRPO's with various radius p's. Middle: relative improvement in worst-case performative risk of the DRPO to the PO as the radius p increases, for different range of misspecification η's. Right: radius p versus estimated KL divergence between Dtrue(θDRPO(p)) and D(θDRPO(p)), where vertical bands indicate the calibrated radius pcal's.

🔼 This algorithm presents the process of Distributionally Robust Performative Risk Minimization. It initializes μ and iteratively updates θ and μ until μ converges. The final output is θ, which represents the solution to the Distributionally Robust Performative Optimum (DRPO) problem. The algorithm involves minimizing the distributionally robust performative risk, which considers the worst-case scenario among a collection of alternative distribution maps.
read the caption
Algorithm 1 DR Performative Risk Minimization
In-depth insights#
Robust Performative Prediction#
Robust performative prediction addresses the challenge of model misspecification in performative prediction settings. Traditional performative prediction methods often rely on accurate modeling of the distribution map – how a model’s deployment changes data distributions. However, real-world distribution maps are complex and difficult to fully capture. Distributionally robust optimization (DRO) techniques offer a promising solution by considering a range of possible distribution maps within an uncertainty set, making the approach robust to model errors and distributional shifts. The framework seeks to minimize the worst-case performative risk across this uncertainty set, yielding solutions that are less susceptible to deviations from the assumed distribution map. This enhances the reliability and generalizability of performative prediction models, particularly in high-stakes applications where unexpected changes in the data environment could have significant negative consequences. The theoretical guarantees and empirical demonstrations highlight the practical benefits of this robust approach to performative prediction.
DRPO: A Robust Solution#
The concept of DRPO (Distributionally Robust Performative Optimum) offers a robust alternative to traditional performative prediction methods. Standard performative prediction relies heavily on accurate modeling of the distribution map, which is often unrealistic due to inherent model misspecification. DRPO addresses this limitation by considering a range of possible distribution maps, thereby mitigating the impact of errors. This robust approach leads to more reliable and stable predictions, even when facing uncertainty in how the model’s deployment affects the data distribution. By incorporating an uncertainty set, DRPO minimizes the worst-case performative risk, providing guarantees of reasonable performance across various scenarios. This approach makes DRPO a more resilient and reliable solution for real-world applications where perfect modeling of the distribution map is an unattainable ideal.
Excess Risk Guarantees#
Excess risk, the difference between a model’s true risk and the optimal risk achievable, is a crucial metric for evaluating model performance, especially when considering the impact of distributional shifts. Distributionally robust performative prediction aims to mitigate the effects of these shifts. A key aspect of evaluating the robustness of such a method lies in providing excess risk guarantees. These guarantees, often expressed as bounds, demonstrate how well the distributionally robust solution approximates the true optimum even under misspecification of the underlying data distribution. Strong duality results often play a vital role in deriving such guarantees. By characterizing the worst-case distribution within a specified uncertainty set, the analysis can determine the maximum possible deviation from the true optimum. The tightness of the derived bound is crucial, as a looser bound may not offer sufficient insights into the practical reliability of the approach. In the context of performative prediction, where model predictions influence future data, excess risk bounds can provide critical assurances about the long-term stability and performance of a deployed model. A smaller excess risk bound indicates higher robustness and better generalizability.
Efficient Optimization#
Efficient optimization is crucial for the practical applicability of distributionally robust performative prediction. The paper highlights the computational challenges associated with solving the distributionally robust performative risk minimization problem and proposes a reformulation that enables efficient optimization. This reformulation leverages strong duality, transforming the original intractable problem into an equivalent, more tractable form. The proposed approach combines theoretical insights with practical algorithmic considerations. An alternating minimization algorithm is suggested to efficiently solve the reformulated problem, iteratively updating model parameters and dual variables until convergence. This approach allows for leveraging existing performative prediction algorithms for efficient solutions, thus demonstrating a significant step towards making distributionally robust performative prediction a viable tool for real-world applications.
Empirical Validation#
An ‘Empirical Validation’ section in a research paper would ideally present robust evidence supporting the study’s claims. This would involve a detailed description of the experimental setup, including the datasets used, and the chosen evaluation metrics. Rigorous statistical analysis is crucial, demonstrating the significance of any observed effects and accounting for potential biases. The results should be clearly presented, possibly with visualizations like graphs and tables, to facilitate understanding and comparison of different approaches. A discussion of limitations is also important, acknowledging any weaknesses in the experimental design or potential confounding factors that might affect the interpretation of results. Finally, the section should effectively connect the empirical findings back to the paper’s central hypothesis or research questions, explaining how the results confirm, refute, or partially support the claims made. Ideally, the findings should also be interpreted within the context of existing literature, highlighting both similarities and differences to prior work. Reproducibility is also key; the description needs to be sufficiently detailed for others to replicate the study.
More visual insights#
More on figures

🔼 This figure presents the results of Experiment 5.1, focusing on strategic classification with a misspecified cost function. The left panel shows the performative risk for different models (PO and DRPO with varying radius p). The middle panel illustrates the relative improvement in worst-case performative risk achieved by DRPO compared to PO across various levels of misspecification (η). Finally, the right panel displays the relationship between the radius p and the estimated KL divergence, highlighting the calibrated radius pcal.
read the caption
Figure 1: Results of Experiment 5.1. Left: performative risk incurred by the PO and the DRPO's with various radius p's. Middle: relative improvement in worst-case performative risk of the DRPO to the PO as the radius p increases, for different range of misspecification η's. Right: radius p versus estimated KL divergence between Dtrue(@DRPO(p)) and D(@DRPO(p)), where vertical bands indicate the calibrated radius pcal's.
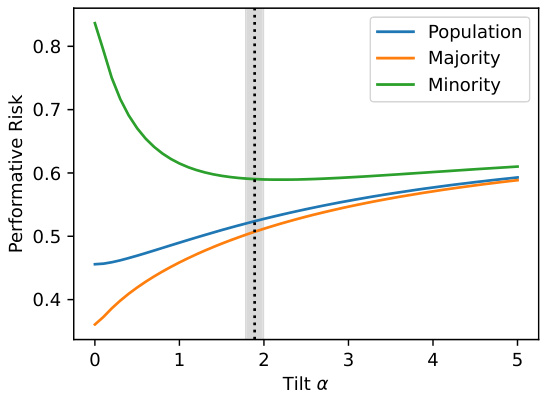
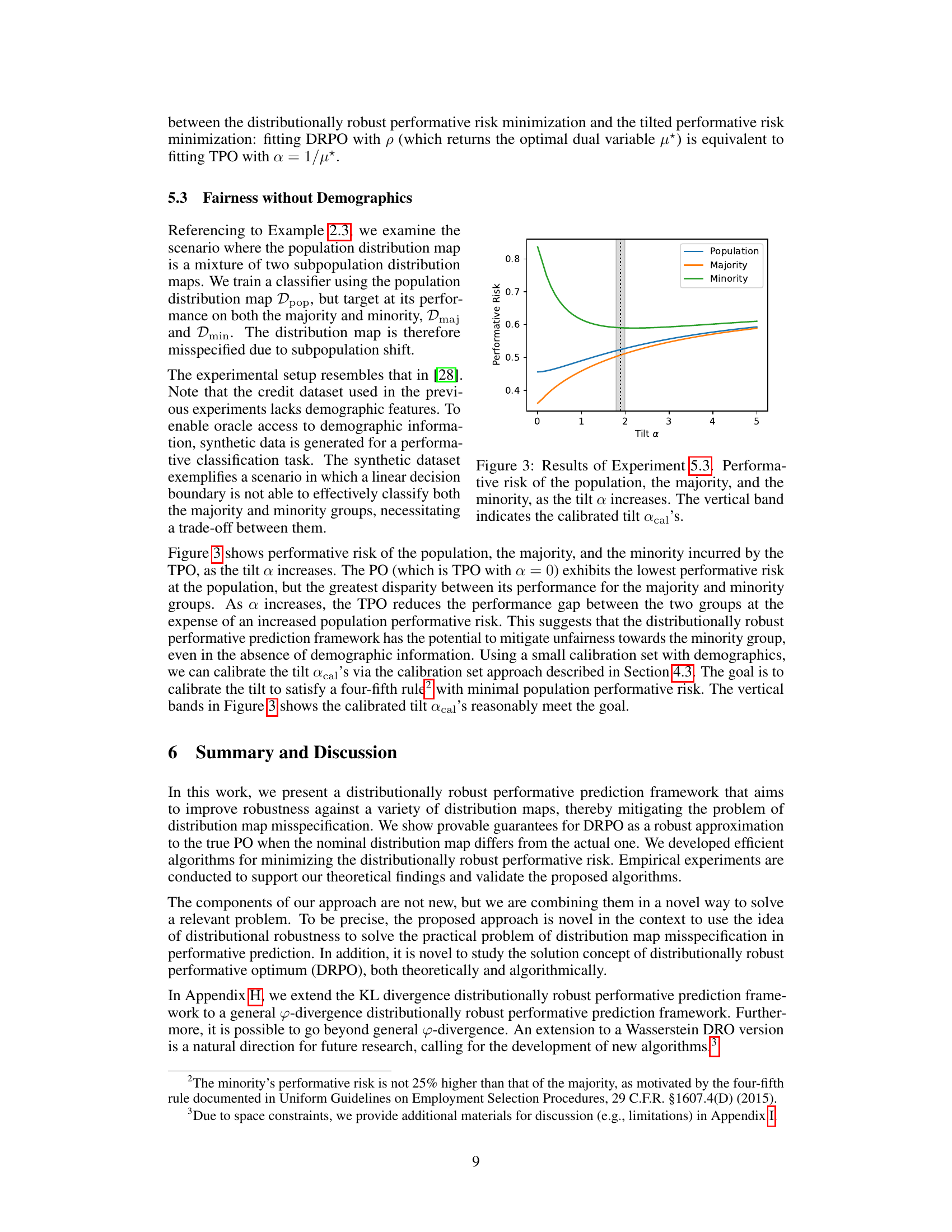
🔼 This figure shows how the performative risk changes for the overall population, the majority group, and the minority group as the tilt parameter α is increased. The performative risk is a measure of the model’s performance on the specific group, considering the impact of the model’s predictions on the data distribution. The vertical band represents the calibrated value of α (αcal), which aims to find a balance between minimizing the overall risk and reducing the performance disparity between the majority and minority groups. It shows that increasing α reduces the performance gap between the two groups but at the expense of increased risk for the overall population.
read the caption
Figure 3: Results of Experiment 5.3. Performative risk of the population, the majority, and the minority, as the tilt α increases. The vertical band indicates the calibrated tilt αcal's.
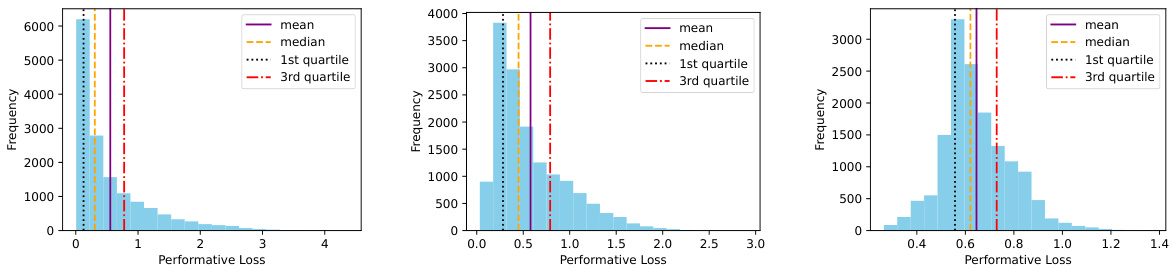
🔼 This figure displays the distribution of performative losses for the PO and DRPO under different radius values (p=0.02 and p=0.04) in Experiment 5.1 where the true performativity level is 0.5. The histograms visually demonstrate how the DRPO, particularly with larger radius values, leads to a more controlled and regulated distribution of losses compared to the PO, mitigating the impact of extreme losses.
read the caption
Figure 4: Histogram of performative loss under Experiment 5.1 with \(\epsilon_{true} = 0.5\). Left: histogram for the PO. Middle: histogram for the DRPO with \(p = 0.02\). Right: histogram for the DRPO with \(p = 0.04\).
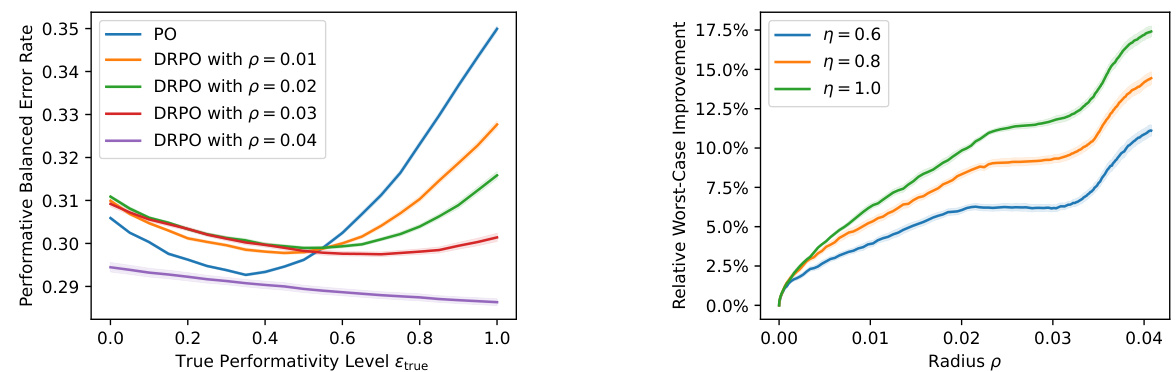
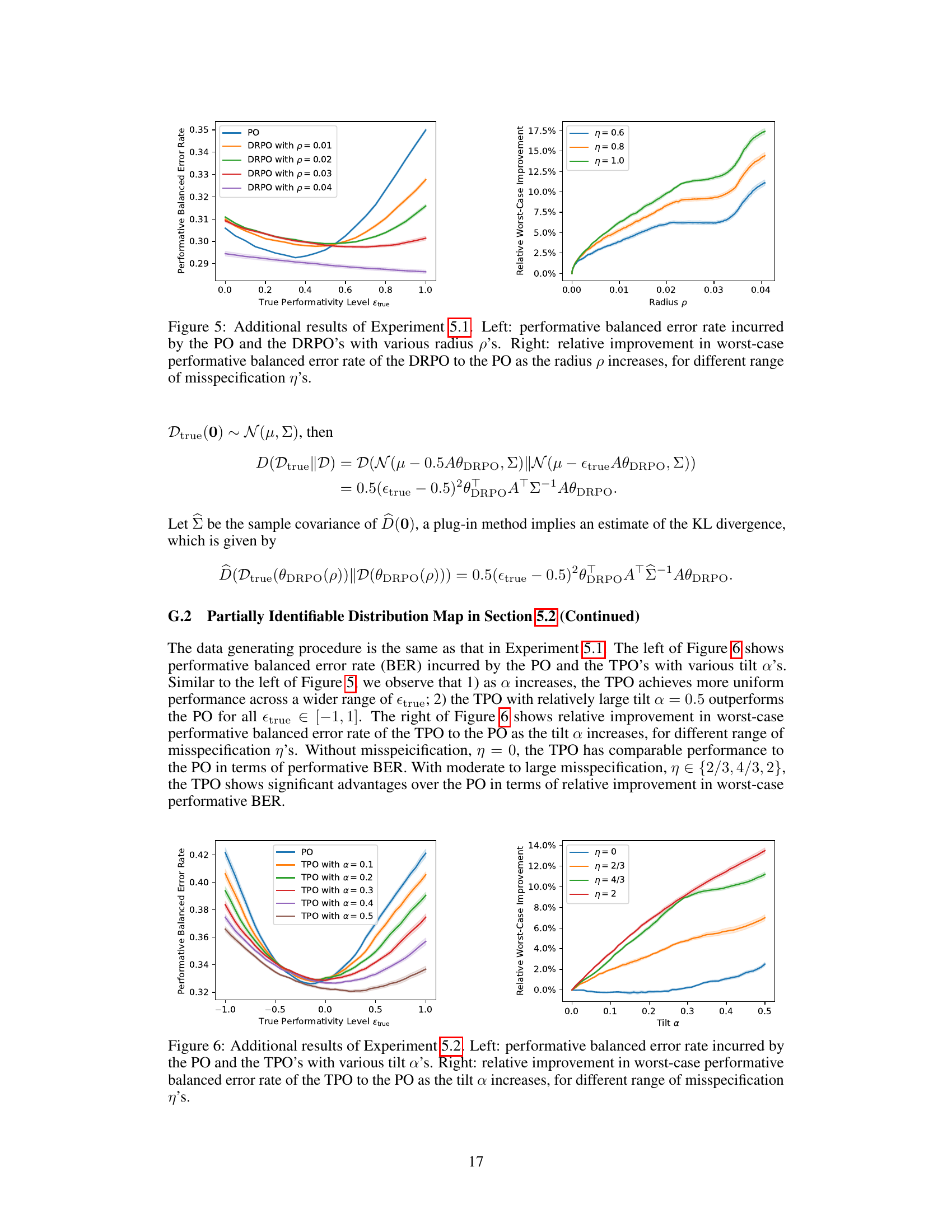
🔼 This figure presents additional results from Experiment 5.1, which focuses on strategic classification with a misspecified cost function. The left panel shows the performative balanced error rate for different models: the standard performative optimum (PO) and distributionally robust performative optimum (DRPO) with varying radii (p). It demonstrates how the DRPO’s performance changes across various true performativity levels (Etrue). The right panel illustrates the relative improvement in worst-case performative balanced error rates achieved by the DRPO compared to the PO, showcasing the robustness of the DRPO against model misspecification for different levels of misspecification (η).
read the caption
Figure 5: Additional results of Experiment 5.1. Left: performative balanced error rate incurred by the PO and the DRPO's with various radius p's. Right: relative improvement in worst-case performative balanced error rate of the DRPO to the PO as the radius p increases, for different range of misspecification η's.
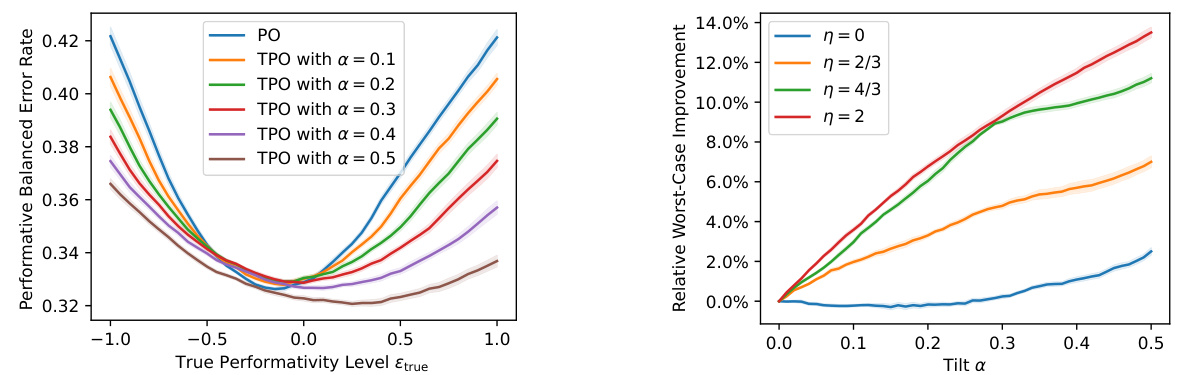
🔼 This figure presents the results of Experiment 5.2, comparing the performance of the PO and TPO methods under different misspecification levels (η). The left panel shows the performative risk for various tilt parameters (α), demonstrating that TPO with larger α values exhibits more uniform performance across a wider range of true performativity levels. The middle panel illustrates the relative improvement in worst-case performative risk achieved by TPO over PO as α increases, highlighting the robustness of TPO for different misspecification levels. Finally, the right panel shows the relationship between the radius (p) and the inverse of the optimal dual variable (μ*), providing insights into the calibration process for these parameters.
read the caption
Figure 2: Results of Experiment 5.2. Left: performative risk incurred by the PO and the TPO's with various tilt a's. Middle: relative improvement in worst-case performative risk of the TPO to the PO as the tilt a increases, for different range of misspecification η's. Right: the correspondence relationship between the radius p and the (inverse of) optimal dual variable μ*.
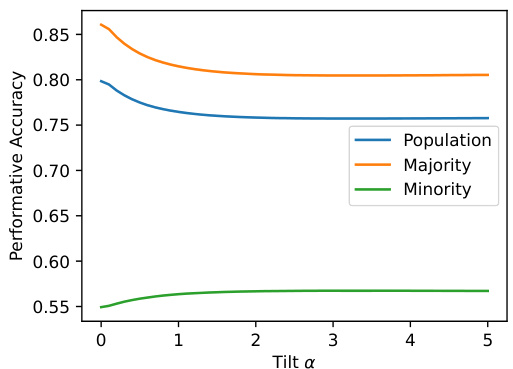
🔼 This figure shows the performative accuracy (accuracy on the model-induced distribution) for the population, majority, and minority groups as the tilt parameter α increases. The PO (α=0) shows the lowest population performative risk but the largest disparity between majority and minority performance. Increasing α reduces the performance gap between groups, though at the cost of slightly lower overall population accuracy. This demonstrates how the distributionally robust approach can mitigate unfairness.
read the caption
Figure 7: Additional results of Experiment 5.3. Performative accuracy of the population, the majority, and the minority, as the tilt α increases.
More on tables

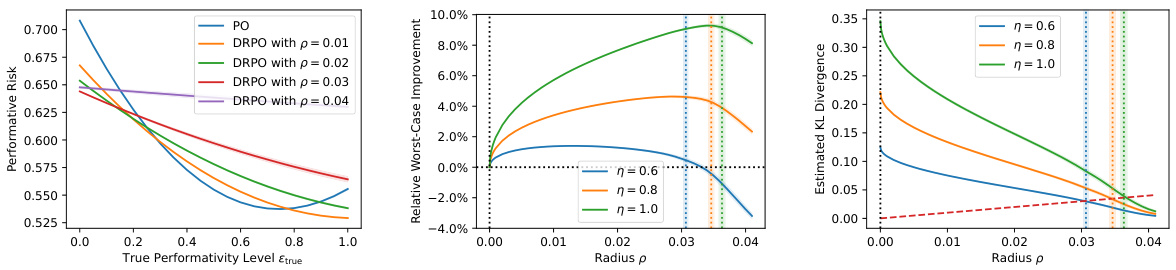
🔼 This figure presents the results of Experiment 5.1, comparing the performance of the PO and DRPO under different misspecification levels. The left panel shows the performative risk for various radius values (p). The middle panel illustrates the relative improvement in worst-case performative risk achieved by DRPO compared to PO for varying degrees of misspecification (η). Finally, the right panel depicts the relationship between the radius p and the estimated KL divergence, showing the calibrated radius (pcal).
read the caption
Figure 1: Results of Experiment 5.1. Left: performative risk incurred by the PO and the DRPO's with various radius p's. Middle: relative improvement in worst-case performative risk of the DRPO to the PO as the radius p increases, for different range of misspecification n's. Right: radius p versus estimated KL divergence between Dtrue(@DRPO(p)) and D(@DRPO(p)), where vertical bands indicate the calibrated radius pcal's.
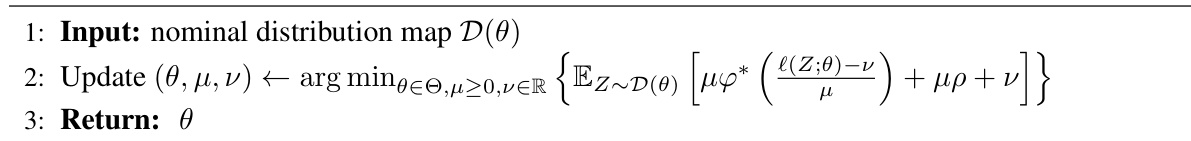
🔼 This figure presents the results of Experiment 5.1, comparing the performance of the PO and DRPO methods under varying misspecification levels (η). The left panel shows the performative risk for different values of the radius (p) and true performativity level (εtrue). The middle panel shows the relative improvement of the DRPO over PO in terms of worst-case performative risk, demonstrating the robustness of the DRPO to misspecification. The right panel illustrates the relationship between the radius (p) and the estimated KL divergence, aiding in the calibration of the radius.
read the caption
Figure 1: Results of Experiment 5.1. Left: performative risk incurred by the PO and the DRPO's with various radius p's. Middle: relative improvement in worst-case performative risk of the DRPO to the PO as the radius p increases, for different range of misspecification η's. Right: radius p versus estimated KL divergence between Dtrue(θDRPO(p)) and D(θDRPO(p)), where vertical bands indicate the calibrated radius pcal's.
Full paper#