Efficient Streaming Algorithms for Graphlet Sampling

↗ arXiv ↗ Hugging Face

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working with massive graphs due to its development of efficient semi-streaming algorithms for graphlet sampling. This addresses a critical limitation of existing methods, paving the way for more efficient analysis of large-scale network data in various machine learning applications. It also provides near-optimal memory and pass tradeoffs, offering valuable insights for algorithm design and optimization in the semi-streaming model.

Visual Insights

#

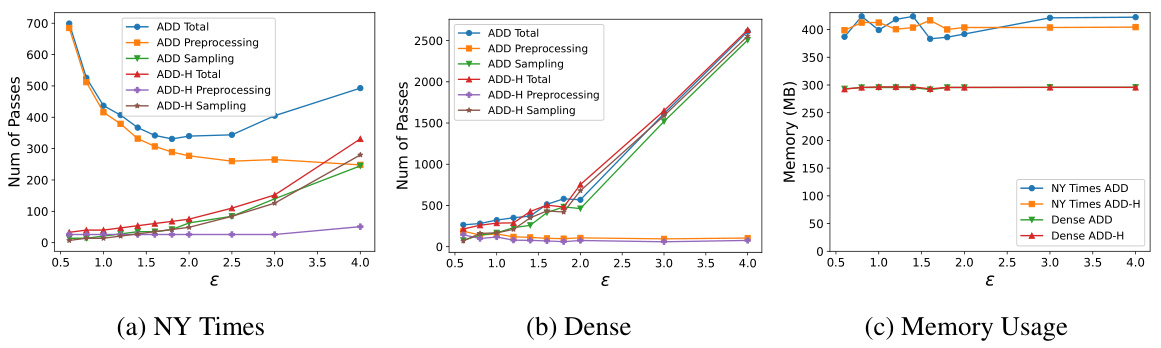
🔼 This figure displays the results of experiments comparing the performance of two algorithms, APPROX-DD and APPROX-DD-HEURISTIC, for computing an approximate degree-dominating order on two datasets (NY Times and Dense). Subfigures (a) and (b) show the number of passes required by each algorithm as a function of epsilon (ε), while subfigure (c) shows the memory usage as a function of epsilon for both algorithms on both datasets. The parameter k is fixed at 4. The results indicate that APPROX-DD-HEURISTIC offers advantages in terms of the number of passes, especially on sparse graphs, while maintaining memory efficiency.

read the caption

Figure 1: The number of passes versus e on NY Times (1a), on Dense (1b), and the memory versus e on two datasets (1c), fixing k = 4. ADD stands for APPROX-DD and ADD-H stands for APPROX-DD-HEURISTIC.

🔼 This table presents the statistics of five datasets used in the experiments. Four real-world datasets (NY Times, Twitter WWW, Twitter MPI, Friendster) were obtained from KONECT, while one synthetic dataset (Dense) was generated with a probability of 0.8 for edge creation.

read the caption

Table 1: Dataset statistics. Dense is generated synthetically by drawing each edge with probability 0.8, and other four datasets are from KONECT.

In-depth insights

#

Stream Graphlets

#

The concept of “Stream Graphlets” blends two powerful ideas: graphlets, small induced subgraphs used to analyze network structure, and streaming algorithms, designed for processing massive datasets that don’t fit in memory. Streaming graphlets would focus on efficiently identifying and analyzing these small subgraphs within a massive graph using a memory-efficient approach. This is crucial because many real-world networks (social networks, biological networks, etc.) are enormous and cannot be loaded into RAM. A streaming graphlet approach would require processing the graph in passes, only keeping a small working memory. The challenge lies in devising algorithms that can accurately sample or count graphlets while making only a few passes over the data stream. This involves carefully designing data structures and algorithms to minimize memory usage and maximize the accuracy of graphlet counts. Research in this area would focus on developing efficient and unbiased sampling techniques to generate representative graphlet statistics within the constraints of limited memory. The ultimate goal is to enable large-scale analysis of complex networks using memory-constrained environments, opening opportunities for new discoveries.

UGS Streaming

#

The concept of “UGS Streaming” likely refers to a streaming algorithm built upon the Uniform Graphlet Sampler (UGS). This suggests a method for efficiently sampling graphlets from massive graphs that cannot fit into main memory. The algorithm would process the graph’s edge list sequentially in passes, using a limited amount of memory (semi-streaming model). Key challenges would include designing efficient data structures and algorithms for tasks such as topological sorting and maintaining sufficient statistical guarantees, while minimizing the number of passes over the data. A core innovation might be adapting UGS’s topological sorting and rejection sampling techniques to the semi-streaming setting, possibly through approximation algorithms to reduce memory footprint and passes. The advantages would be enabling graphlet-based analysis of datasets too large for conventional methods. Potential limitations might involve the trade-off between the number of passes, memory usage, and the accuracy of the sampling, particularly when dealing with very large graphs or complex graph structures. Furthermore, the sampling method might be approximate, thus impacting its statistical properties compared to the exact UGS.

Memory Lower Bounds

#

The heading ‘Memory Lower Bounds’ in a research paper signals a crucial section dedicated to establishing theoretical limits on the minimum memory required by any algorithm solving a specific problem. This is vital for understanding the fundamental efficiency of the proposed approach. The authors likely employ techniques from communication complexity or information theory to prove these lower bounds. This involves demonstrating a connection between the memory usage of an algorithm and the information needed to solve the problem, often using reduction arguments. A strong lower bound demonstrates that the algorithm’s memory usage is close to optimal, implying that significant improvements in efficiency will be hard to achieve with only algorithmic optimization. This section provides a strong theoretical justification for the space-efficiency of proposed solutions by proving that no algorithm can achieve better space complexity than the one established in this section. The results of this analysis helps to evaluate the performance of the proposed approach within the context of the inherent computational constraints for solving the problem, highlighting the space-efficiency of the chosen algorithm.

Algorithm Passes

#

The concept of ‘Algorithm Passes’ in streaming algorithms, particularly within the context of graph processing, is crucial for efficiency. It represents the number of times the algorithm needs to read the entire input data (e.g., the edge list of a graph). Minimizing the number of passes is paramount because each pass can be computationally expensive, especially for massive datasets that don’t fit into main memory. The design of algorithms that use a limited number of passes, such as logarithmic passes, is a major focus for achieving scalability. Tradeoffs between the number of passes and memory usage are often explored. Algorithms with fewer passes might require more memory, and vice-versa. The optimal balance depends on resource constraints. The analysis of algorithm passes involves considering the different phases of the algorithm. Preprocessing steps might have different pass complexities than the sampling phases. Also, parallelization techniques can be incorporated to reduce overall pass count, but their impact needs to be evaluated in the context of the algorithm’s memory use and computational cost.

Future Work

#

The authors suggest several avenues for future research. Extending the semi-streaming algorithms to handle dynamic graphs is a crucial next step, as real-world graphs are constantly evolving. This would involve efficiently incorporating edge insertions and deletions into the existing framework, potentially using techniques like incremental graph processing. Another important direction is exploring the trade-offs between memory and the number of passes more systematically. This involves a deeper theoretical analysis to identify optimal memory-pass configurations under different graph characteristics and algorithm constraints. Finally, the authors highlight investigating the effectiveness of their algorithm on various real-world graph datasets across diverse domains and sizes to broaden its applicability and evaluate its robustness. This would involve rigorous empirical testing and comparative analysis against existing state-of-the-art graphlet sampling methods. A further consideration is developing parallel semi-streaming algorithms to leverage modern multi-core architectures for faster graphlet sampling, especially on massive graphs.

More visual insights

#

More on tables

🔼 This table presents the characteristics of five datasets used in the paper’s experiments. The datasets include one synthetic dataset (‘Dense’) and four real-world datasets from the KONECT repository. For each dataset, the table shows the file size in MB, the number of vertices, and the number of edges.

read the caption

Table 1: Dataset statistics. Dense is generated synthetically by drawing each edge with probability 0.8, and other four datasets are from KONECT.

🔼 This table presents statistics for five datasets used in the paper’s experiments. Four of the datasets (NY Times, Twitter WWW, Twitter MPI, Friendster) are real-world graphs obtained from the KONECT repository. The ‘Dense’ dataset is synthetic, created by randomly assigning edges with a probability of 0.8. For each dataset, the table lists the file size in MB, the number of vertices, and the number of edges.

read the caption

Table 1: Dataset statistics. Dense is generated synthetically by drawing each edge with probability 0.8, and other four datasets are from KONECT.

🔼 This table presents the statistics of five datasets used in the paper’s experiments. Four datasets (NY Times, Twitter, Friendster) were obtained from the KONECT repository, while one dataset (Dense) was generated synthetically by assigning a probability of 0.8 to the creation of each edge. The table shows the file size of each dataset in MB, the number of vertices, and the number of edges.

read the caption

Table 1: Dataset statistics. Dense is generated synthetically by drawing each edge with probability 0.8, and other four datasets are from KONECT.

🔼 This table presents the statistics of five datasets used in the paper’s experiments. Four real-world datasets were obtained from the KONECT network collection, while one dataset (‘Dense’) was synthetically generated with a specified edge probability (0.8). The table shows the file size, number of vertices, and number of edges for each dataset. This information is crucial for understanding the scale and characteristics of the data used in evaluating the proposed streaming algorithms.

read the caption

Table 1: Dataset statistics. Dense is generated synthetically by drawing each edge with probability 0.8, and other four datasets are from KONECT.

🔼 This table presents statistics for five graph datasets used in the paper’s experiments. Four datasets (NY Times, Twitter WWW, Twitter MPI, Friendster) were obtained from the KONECT repository. One dataset (Dense) was synthetically generated with an edge probability of 0.8 to represent a dense graph. The table lists the file size of each dataset in MB, the number of vertices (nodes), and the number of edges.

read the caption

Table 1: Dataset statistics. Dense is generated synthetically by drawing each edge with probability 0.8, and other four datasets are from KONECT.

Full paper

#