↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many machine learning problems benefit from models that adapt to the structure of their data, often concentrating on low-dimensional manifolds. A common approach is to regularize the model’s Jacobian, encouraging it to behave like a low-rank linear map locally. However, directly penalizing the Jacobian’s rank is challenging due to non-differentiability, leading researchers to consider the nuclear norm (sum of singular values), a convex relaxation of the rank. The computational cost of computing and using the Jacobian nuclear norm penalty in high-dimensional settings has, however, hindered its widespread adoption. This is the main problem the authors sought to address.
This work provides a solution to this computational bottleneck. The authors prove that for functions parametrized as compositions of simpler functions (common in deep learning), one can equivalently penalize the average squared Frobenius norms of the Jacobians of the composing functions. This avoids the expensive singular value decomposition. They further introduce a denoising-style approximation that entirely eliminates the need for Jacobian computations. Through theoretical analysis and empirical studies on denoising and representation learning tasks, they demonstrate the efficacy and scalability of their approach, making Jacobian nuclear norm regularization practical for high-dimensional deep learning problems. This efficient and accurate method is a significant step forward in scaling Jacobian nuclear norm regularization to high-dimensional deep learning.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in deep learning and related fields because it introduces an efficient and accurate method for Jacobian nuclear norm regularization. This addresses a critical limitation in scaling existing regularization techniques to high-dimensional problems and could significantly improve the performance and generalizability of deep learning models. The proposed method also opens new avenues for research into locally low-rank functions and their applications in various machine learning tasks such as denoising and representation learning.
Visual Insights#

This figure compares the exact solutions of problems (8) and (9) with their respective neural network approximations for two different values of the regularization parameter (η). Problem (8) involves directly minimizing the Jacobian nuclear norm, while problem (9) uses the proposed approximation that avoids expensive Jacobian computations. The figure visually demonstrates that the proposed method (problem (9)) provides accurate results comparable to the exact solution of problem (8), while having significantly lower computational cost.

The table presents the peak signal-to-noise ratio (PSNR) in decibels (dB) achieved by different denoising methods on held-out images. The methods compared are BM3D, the proposed method, Noise2Noise (N2N), and a supervised method. Results are shown for two noise levels (σ = 1 and σ = 2) and two datasets (Imagenet and CBSD68). The table highlights that the proposed method achieves comparable performance to the supervised denoiser, even when trained only on noisy images.
In-depth insights#
Jacobian Regularization#
Jacobian regularization, a technique to encourage low-rank Jacobian matrices in deep learning models, aims to constrain the model’s local behavior. This is motivated by the manifold hypothesis, suggesting that real-world data often lies on low-dimensional manifolds embedded within high-dimensional spaces. By penalizing the nuclear norm of the Jacobian, the method encourages the model to be insensitive to variations orthogonal to the data manifold, resulting in improved generalization and robustness. The main challenge lies in computational cost; calculating and decomposing the Jacobian matrix can be computationally expensive, especially in high-dimensional settings. Efficient approximations are crucial, such as exploiting the compositionality of deep networks or using stochastic trace estimators to avoid the explicit Jacobian calculation, making Jacobian regularization a practical tool for improving model behavior. Furthermore, the choice of regularization strength requires careful consideration; over-regularization can restrict model expressiveness, while under-regularization may not significantly improve performance. Therefore, careful tuning and validation are vital for successful implementation.
Efficient Training#
Efficient training of deep learning models is crucial for practical applications. This often involves addressing computational bottlenecks arising from large datasets and complex architectures. Strategies for efficient training include techniques like model parallelism, where different parts of the model are trained on different devices, and data parallelism, distributing data across multiple machines. Optimization algorithms play a vital role, with methods like AdamW often preferred for their effectiveness and speed. Furthermore, regularization techniques such as weight decay or dropout prevent overfitting and improve generalization, indirectly contributing to efficiency by reducing the need for extensive training. Hardware acceleration using GPUs or TPUs significantly speeds up the training process. Finally, efficient training also requires careful consideration of hyperparameter tuning. Automated hyperparameter optimization methods can accelerate this process and discover optimal parameter settings for faster and more efficient training.
Denoising & Learning#
The concept of ‘Denoising & Learning’ in the context of deep learning involves techniques that simultaneously remove noise from data and learn underlying representations. Noise reduction is crucial because noisy data can hinder the learning process, leading to poor generalization and inaccurate models. The paper explores a novel approach to this problem by leveraging the Jacobian nuclear norm as a regularizer. This method, unlike traditional methods, does not require computationally expensive singular value decompositions (SVDs). Instead, it leverages the structure of deep learning models (compositions of functions) to efficiently approximate the Jacobian’s nuclear norm. This allows scaling to higher-dimensional deep learning problems, which are often intractable for traditional nuclear norm regularization. The paper demonstrates the effectiveness of the proposed method in denoising tasks, particularly achieving results comparable to fully supervised methods while trained exclusively on noisy data. Furthermore, its utility extends to representation learning, enabling the learning of low-dimensional representations that are semantically meaningful. The key strength of this approach lies in its efficiency and scalability, making Jacobian nuclear norm regularization a practical tool for applications where both noise reduction and representation learning are critical.
Theoretical Analysis#
A theoretical analysis section in a research paper would rigorously justify the claims made. It would likely involve mathematical proofs to validate core algorithms or models, potentially using established theorems or developing novel mathematical concepts. The analysis would focus on the correctness and efficiency of methods, establishing bounds on computational complexity or error rates. Assumptions and limitations of the theoretical results would be clearly stated, acknowledging boundary conditions or constraints under which the findings hold true. The section could also explore the relationships between different variables and delve into theoretical implications beyond the immediate application, establishing the broader relevance and significance of the work. Ultimately, a strong theoretical analysis contributes to the overall credibility and impact of the research by providing a solid foundation of mathematical reasoning.
Future Extensions#
Future work could explore several promising avenues. Extending the theoretical analysis to more complex deep learning architectures, beyond compositions of two functions, is crucial. The current approach’s reliance on the chain rule for Jacobians necessitates a deeper investigation into handling more intricate network structures. Developing more sophisticated Jacobian approximation techniques is another vital direction. The current method uses a first-order Taylor approximation and Hutchinson’s trace estimator, which could be enhanced with higher-order methods or alternative stochastic estimators for improved accuracy and efficiency. Finally, broadening the range of applications is key. While denoising and representation learning are compelling starting points, the Jacobian nuclear norm regularizer’s potential extends to various other problems, including those dealing with robustness, generalization, and inverse problems. Further investigation into these areas would uncover the full potential of the proposed technique.
More visual insights#
More on figures
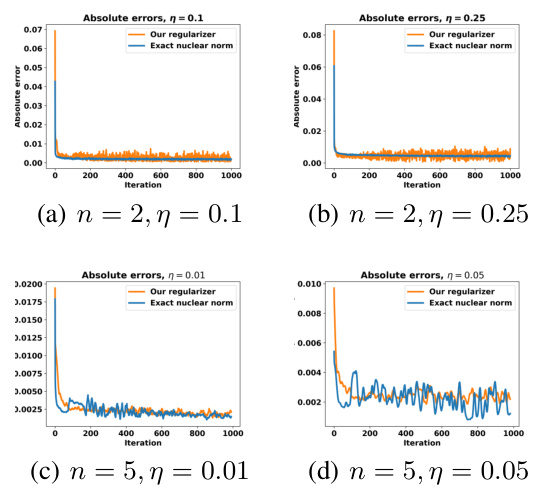
This figure compares the mean absolute error of neural network solutions to two optimization problems: one directly penalizing the Jacobian nuclear norm and the other using the authors’ proposed Jacobian-free regularizer. Across different dimensions (n=2, n=5) and regularization strengths (η), the proposed method consistently achieves accuracy similar to the computationally expensive nuclear norm method. This demonstrates the efficacy and efficiency of the proposed regularizer.
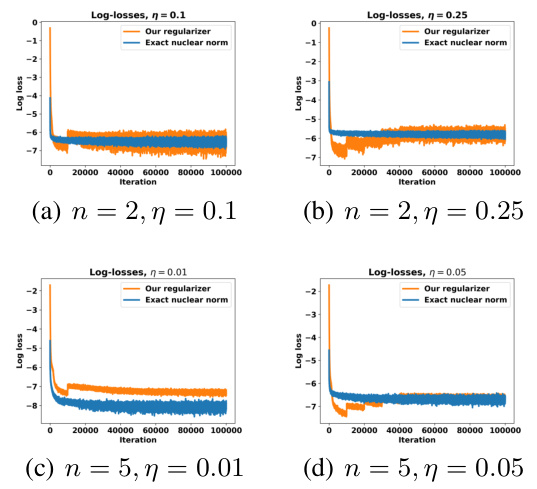
This figure compares the accuracy of neural network solutions to two different optimization problems: problem (8), which involves directly penalizing the Jacobian nuclear norm, and problem (9), which uses the proposed Jacobian-free regularizer. The plot shows the mean absolute error of the solutions over training iterations. The results demonstrate that the proposed method achieves comparable accuracy to the traditional approach despite avoiding computationally expensive Jacobian computations. The figure consists of four subplots, each corresponding to a different setting of dimensionality (n=2 or n=5) and regularization strength (η=0.1, 0.25, 0.01, or 0.05).

This figure compares the performance of different denoising methods on images corrupted with Gaussian noise. The first row shows results with a noise standard deviation (σ) of 1, and the second row shows results with σ = 2. Methods compared include BM3D, the proposed method, Noise2Noise (N2N), and a supervised denoiser. The figure demonstrates that the proposed method achieves denoising performance comparable to the supervised method, even though it was trained only on noisy images.
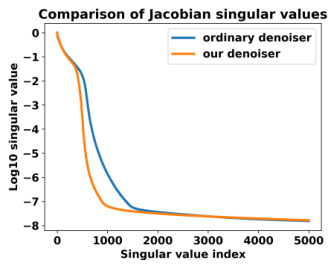
This figure compares the singular values of the Jacobian matrices of a supervised denoiser and the proposed denoiser. The singular values are plotted on a logarithmic scale against their index. The decay of the singular values for the proposed denoiser is steeper than for the supervised denoiser indicating the effectiveness of Jacobian regularization in promoting low-rank Jacobians for the proposed method.

This figure shows the result of traversing the latent space of an unregularized autoencoder along the directions given by the left singular vectors of its Jacobian matrix. The images demonstrate that these traversal directions primarily affect the color of the output images, leaving other features unchanged. This highlights a limitation of the unregularized model; it does not learn to manipulate semantically meaningful attributes of the image. This contrasts with the results shown in Figure 7, which shows traversals of the regularized autoencoder, exhibiting more meaningful changes to the image features.

This figure shows the results of traversing the latent space of an unregularized autoencoder along the directions of its Jacobian’s singular vectors. The image shows how changes in these directions primarily affect the color palette of the generated images, without altering other facial features or attributes. This demonstrates a limitation of the model in capturing rich variations in the data; it suggests that the model’s latent representation doesn’t fully capture the semantic meaning of different aspects of faces.

This figure shows the results of traversing the latent space of an unregularized autoencoder along the Jacobian singular vectors. The images show that changes in the latent space primarily affect the colors of the generated faces, while other features like facial expressions remain largely unchanged, highlighting the limitations of the model’s ability to capture semantic variations.
Full paper#



















