↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Traditional methods for solving extensive-form games, like Counterfactual Regret Minimization (CFR) and its variants, struggle with the computational complexity of large-scale games. Many CFR variants are unsuitable for Monte Carlo settings, limiting their application to real-world scenarios. Furthermore, finding an equilibrium in incomplete information games is significantly more challenging than in complete information games, due to the inability to directly use subgame payoffs in backward induction.
This paper introduces MCCFVFP, a new algorithm that addresses these limitations. By cleverly combining CFR’s counterfactual value calculations with the efficiency of Fictitious Play’s best response strategy, MCCFVFP achieves convergence speeds 20-50% faster than state-of-the-art MCCFR variants in poker and other test games. The algorithm is particularly effective in games with many dominated strategies, a common characteristic of large-scale games. This improvement is significant because it enhances the ability to train and deploy game AI in more realistic and complex situations.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on large-scale game AI. It introduces a novel algorithm, MCCFVFP, that significantly improves convergence speed in extensive-form games. This is particularly relevant to current research trends focusing on efficient game solving techniques for complex scenarios, opening new avenues for developing more effective game AI and offering valuable insights for algorithm design.
Visual Insights#
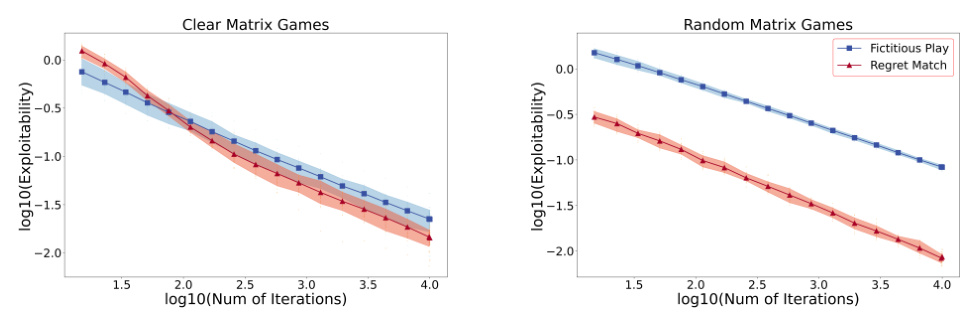
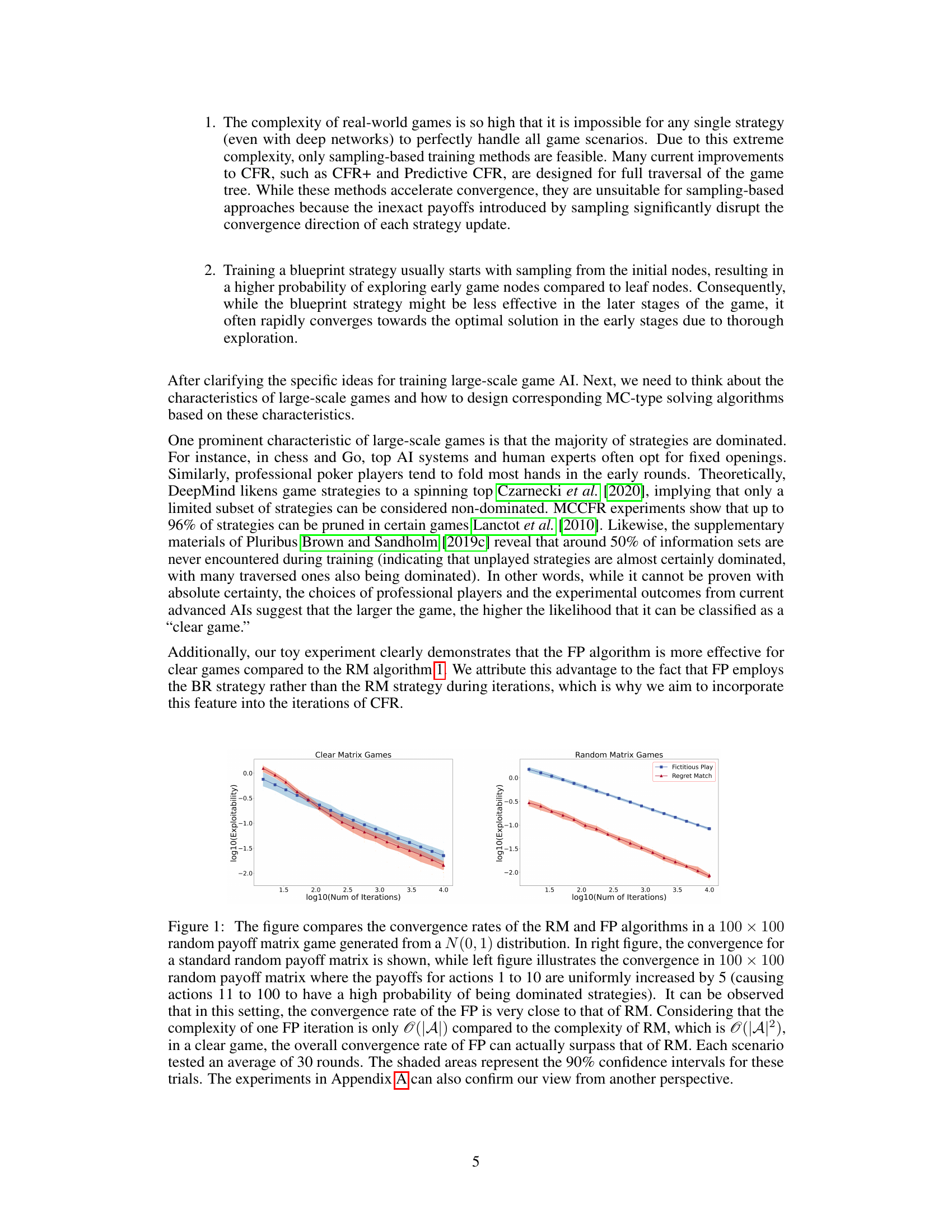
This figure compares the convergence speed of Regret Matching (RM) and Fictitious Play (FP) in two types of 100x100 matrix games: a standard random game and a ‘clear’ game where a subset of actions are dominated. The results show that in clear games, FP converges faster, highlighting its advantage when many strategies are clearly inferior.

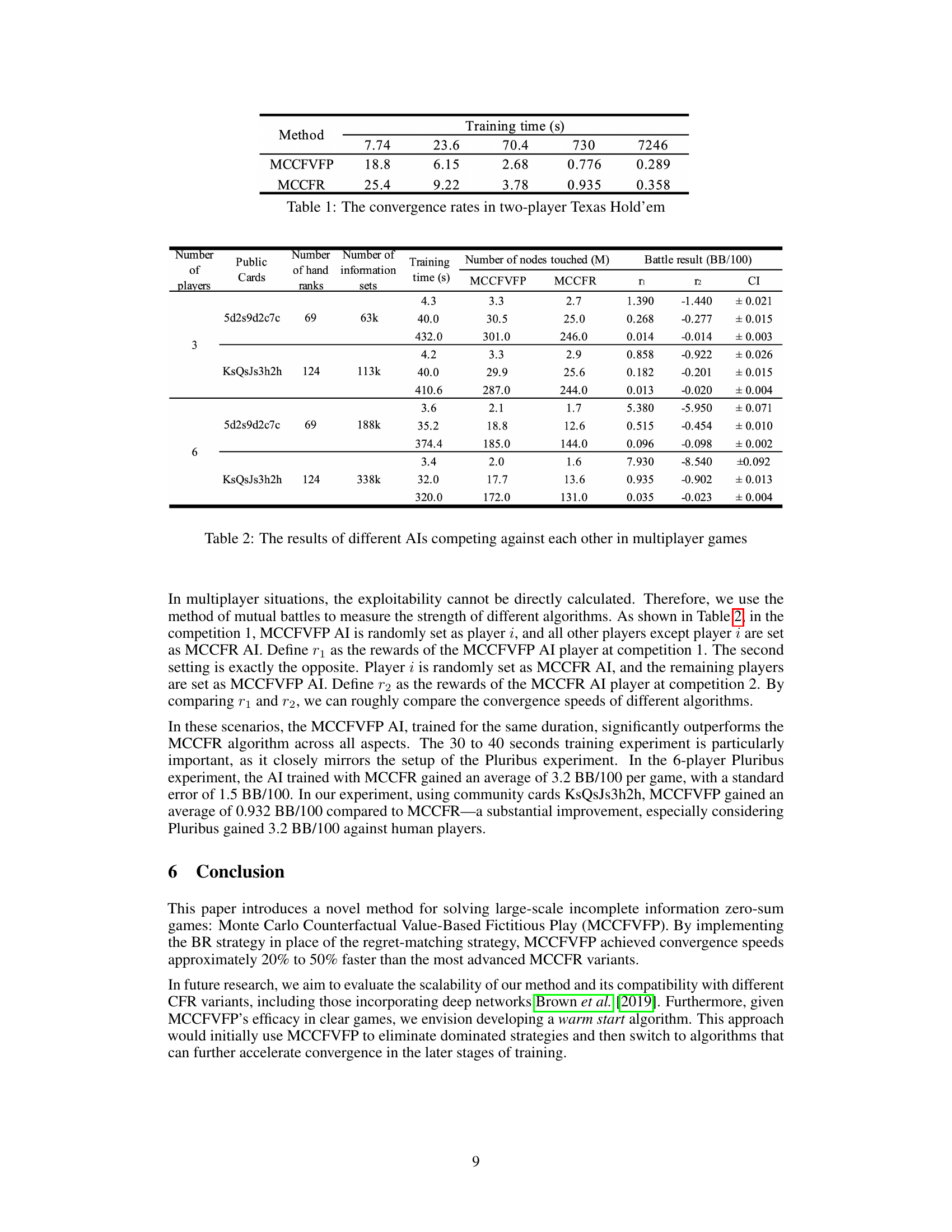
The table shows the convergence speed of MCCFVFP and MCCFR algorithms in a two-player Texas Hold’em game. The training time (in seconds) is presented for different game scales, demonstrating the improved convergence of MCCFVFP, especially as the game size increases.
In-depth insights#
MCCFVFP Algorithm#
The proposed MCCFVFP algorithm represents a novel approach to solving extensive-form games, particularly focusing on accelerating Nash equilibrium convergence in Monte Carlo settings. It cleverly integrates the strengths of Counterfactual Regret Minimization (CFR) and Fictitious Play (FP), specifically leveraging CFR’s counterfactual value calculations for informed decision-making and FP’s best response strategy to efficiently handle games with many dominated strategies. This hybrid approach addresses the limitations of existing MC-based CFR variants, which often struggle with convergence speed in large-scale games. By using a best response strategy instead of regret matching, MCCFVFP reduces computational complexity and allows for effective pruning of the game tree. Theoretical analysis suggests that MCCFVFP offers significant computational advantages over traditional MCCFR, requiring fewer calculations per information set and benefiting from inherent pruning mechanisms. Experimental results demonstrate faster convergence speeds for MCCFVFP compared to state-of-the-art MCCFR variants across several game types, highlighting the algorithm’s practical effectiveness in handling large-scale problems. Further research into the algorithm’s performance across various game characteristics, alongside exploration of other weighted averaging schemes, could further improve its efficiency and broaden its applicability.
Convergence Speedup#
The research paper explores methods to accelerate convergence in solving extensive-form games, a significant challenge in AI. A core focus is enhancing the speed at which algorithms reach Nash Equilibrium. The paper introduces MCCFVFP, a novel algorithm leveraging the strengths of both Counterfactual Regret Minimization (CFR) and Fictitious Play (FP). MCCFVFP demonstrably achieves faster convergence than existing state-of-the-art methods like MCCFR, particularly in large-scale games with a high proportion of dominated strategies. This speedup is attributed to the algorithm’s efficient use of best-response strategies and counterfactual values, combined with effective pruning techniques. The results show significant improvements in convergence speed, approximately 20-50% faster than MCCFR variants across various game types. Theoretical analysis supports the observed speedup, highlighting reduced computational complexity and efficient node traversal. However, the algorithm’s performance might be impacted by the proportion of dominated strategies in the game. Future work could focus on improving its performance in game scenarios with fewer dominated strategies and further enhancing its scalability for even larger-scale game applications.
Dominated Strategies#
The concept of ‘dominated strategies’ is central to game theory and algorithm design, particularly when dealing with large-scale games. A dominated strategy is one that always yields a lower payoff than another strategy, regardless of the opponent’s actions. In such games, identifying and eliminating these dominated strategies can significantly simplify the game and improve the convergence speed of algorithms searching for Nash Equilibrium. Identifying and leveraging dominated strategies, as in the Fictitious Play algorithm (FP), or through pruning in Monte Carlo Counterfactual Regret Minimization (MCCFR), is crucial for efficient game solving. The proportion of dominated strategies in a game, which the authors classify as ‘clear’ or ’tangled’ games, directly affects the effectiveness of various algorithms. The paper demonstrates how using the best response strategy, inspired by FP, and combined with counterfactual value calculations, allows for significant speed improvements, especially in games with a high percentage of dominated strategies. This approach is particularly relevant for large-scale games that are computationally challenging, enabling faster convergence to Nash Equilibrium by intelligently focusing on relevant strategic choices.
Large-Scale Games#
Large-scale games, characterized by vast state and action spaces, pose significant challenges for traditional game-solving techniques. The sheer size of these games often renders exhaustive search methods infeasible, demanding the development of more efficient algorithms. Sampling-based approaches, like Monte Carlo Counterfactual Regret Minimization (MCCFR), become crucial for handling such complexity, but even these methods can struggle with convergence speed. Many large-scale games exhibit a high proportion of dominated strategies, a feature that can be leveraged for algorithmic improvements. The paper explores this characteristic to develop a novel algorithm which significantly accelerates convergence in these types of games. The identification and exploitation of dominated strategies is key to the effectiveness of their proposed method, suggesting that future research should investigate other structural properties of large games for further efficiency gains. Careful consideration of the tradeoffs between convergence speed and computational cost is paramount when designing algorithms for this setting.
Future Research#
Future research directions stemming from this work could explore several promising avenues. Extending MCCFVFP’s applicability to more complex game structures beyond those tested is crucial, particularly those with less clear dominance patterns. Investigating the algorithm’s performance across a wider range of CFR variants and weighted averaging schemes will reveal its adaptability and robustness. A thorough theoretical analysis to refine the convergence rate bounds would provide a deeper understanding of its efficiency. Finally, combining MCCFVFP with deep learning techniques or real-time search, as done in state-of-the-art game playing AI, could produce powerful hybrid algorithms for tackling extremely large-scale games where neither method alone is sufficient. This integration presents a significant opportunity to enhance the speed and efficacy of AI decision-making in complex, real-world scenarios.
More visual insights#
More on figures
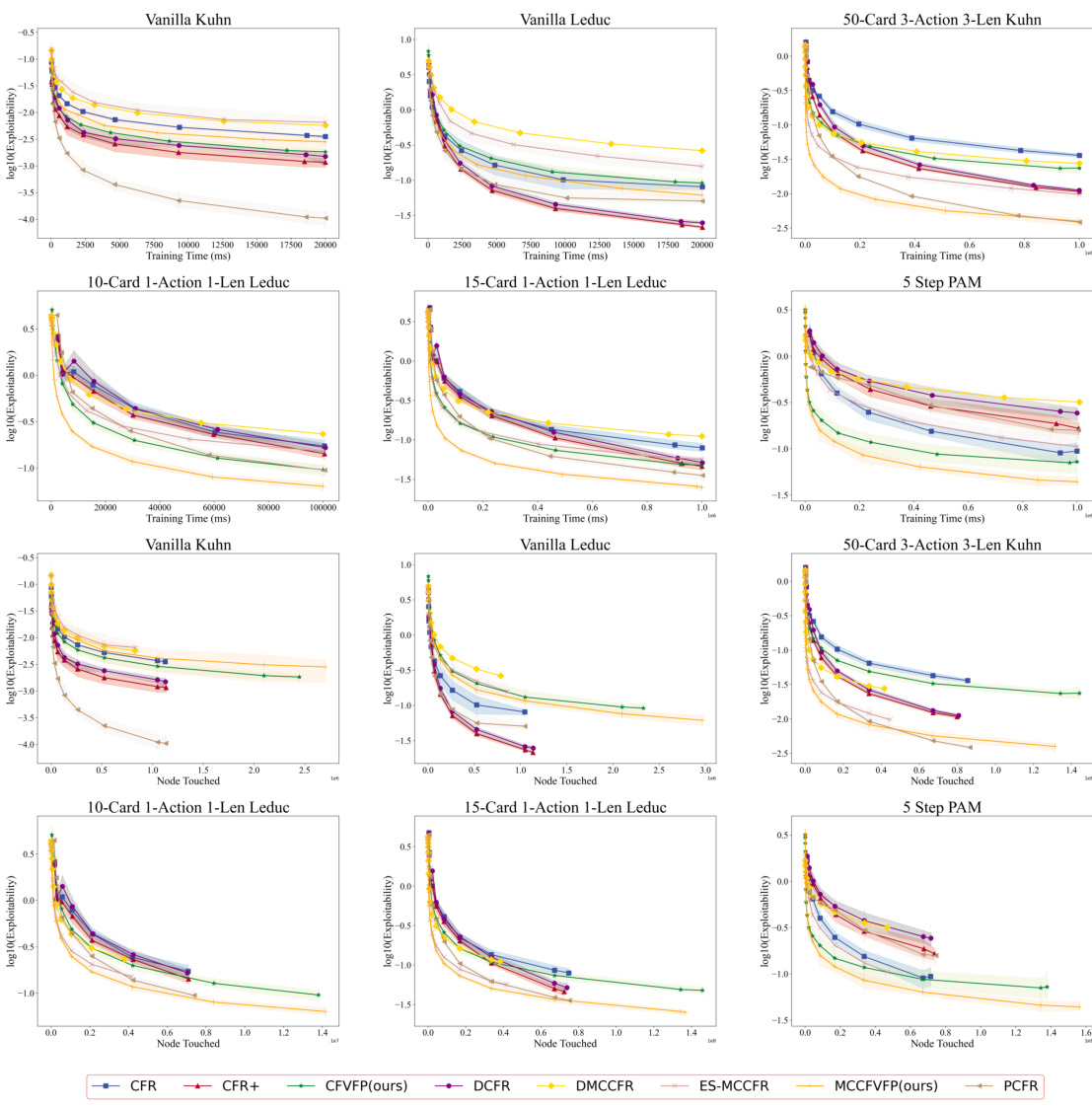
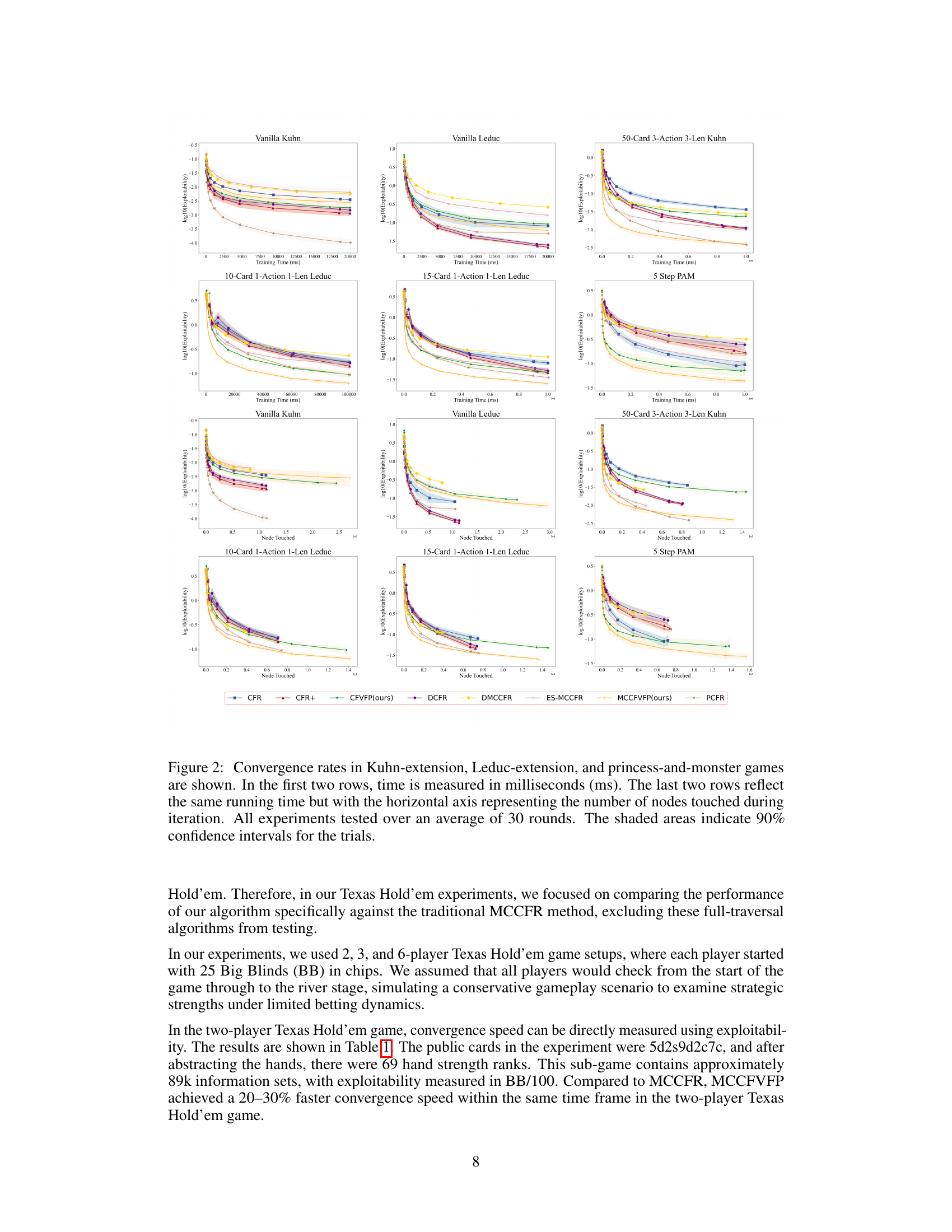
This figure compares the convergence speed of different algorithms across various games, showing the exploitability (a measure of how far from Nash Equilibrium the strategies are) over time (in milliseconds or nodes touched). The top two rows show convergence time in milliseconds; the bottom two rows show convergence speed using the number of nodes touched as the metric. The shaded areas represent 90% confidence intervals. The goal is to demonstrate that MCCFVFP consistently converges faster than MCCFR, especially as the game scale increases.

This figure illustrates the difference in the forceable half-spaces for Regret Matching (RM) and Fictitious Play (FP, specifically CFVFP in this context) strategies in a two-dimensional plane. It visually represents how the choice of strategy (RM or BR) affects the region (half-space) in which the regret vector must fall to guarantee convergence towards the target set (S²). The figure highlights that the BR strategy employed by FP provides a larger, more encompassing half-space, implying it’s more efficient at achieving convergence.
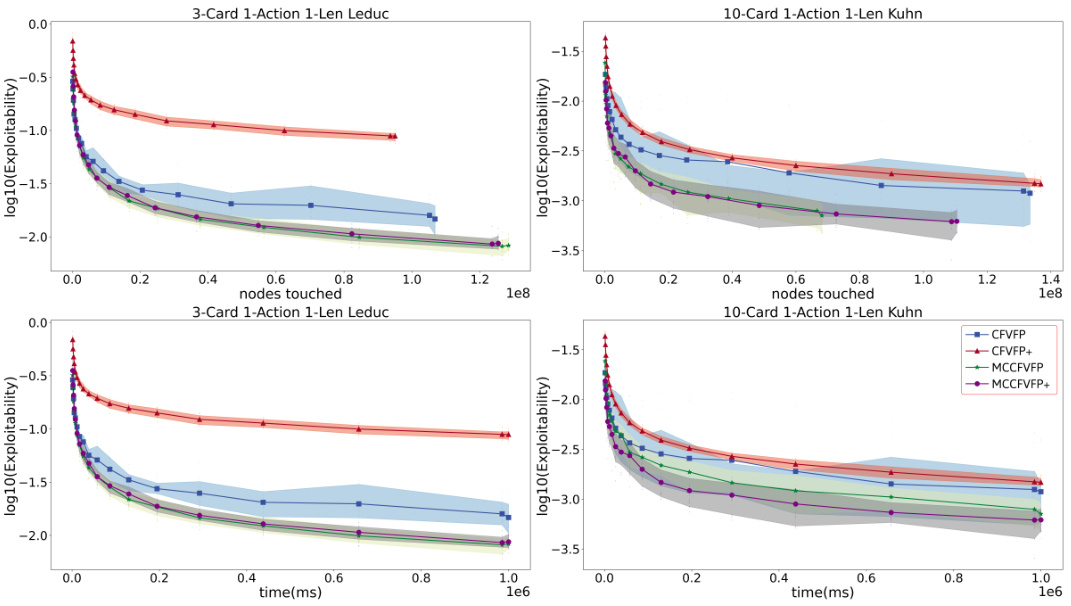
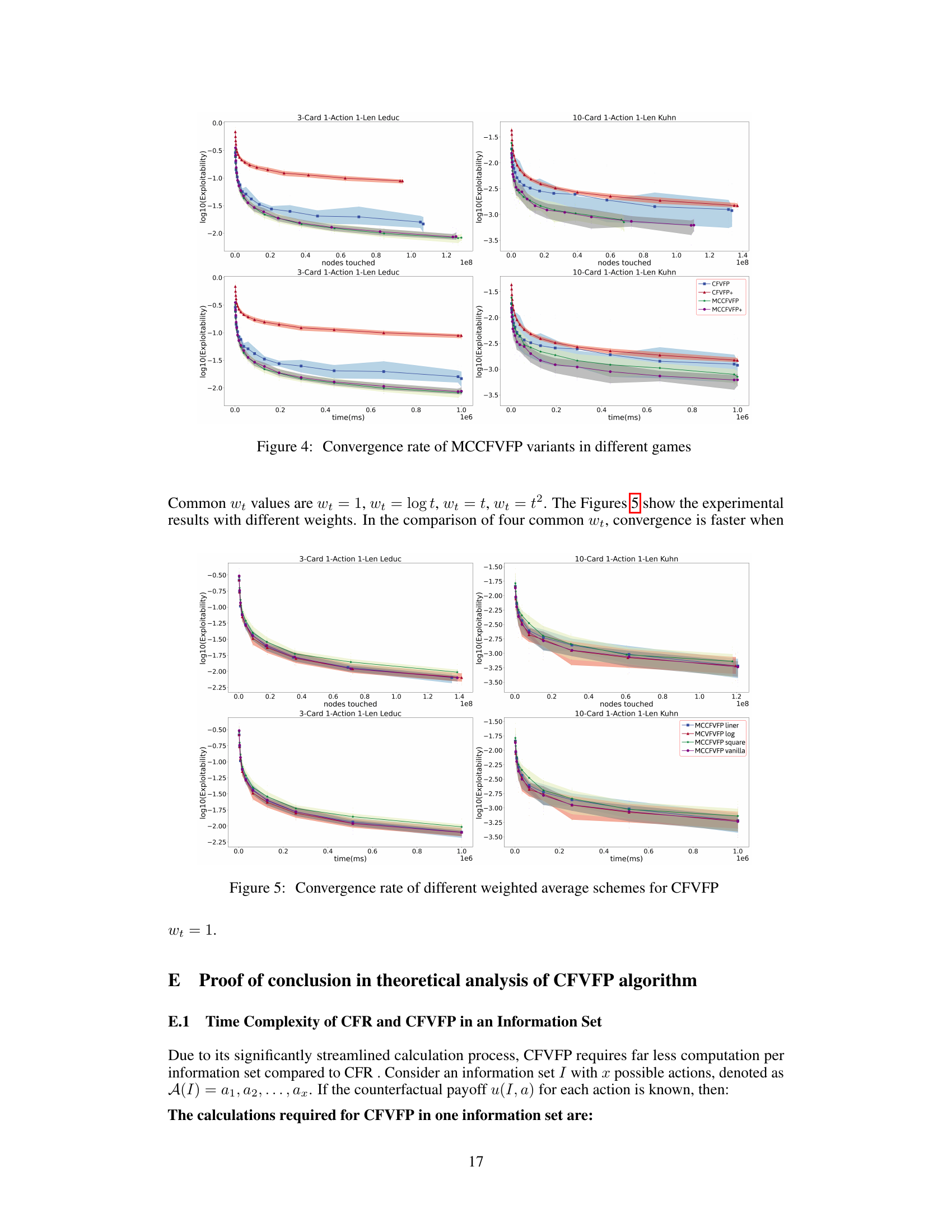
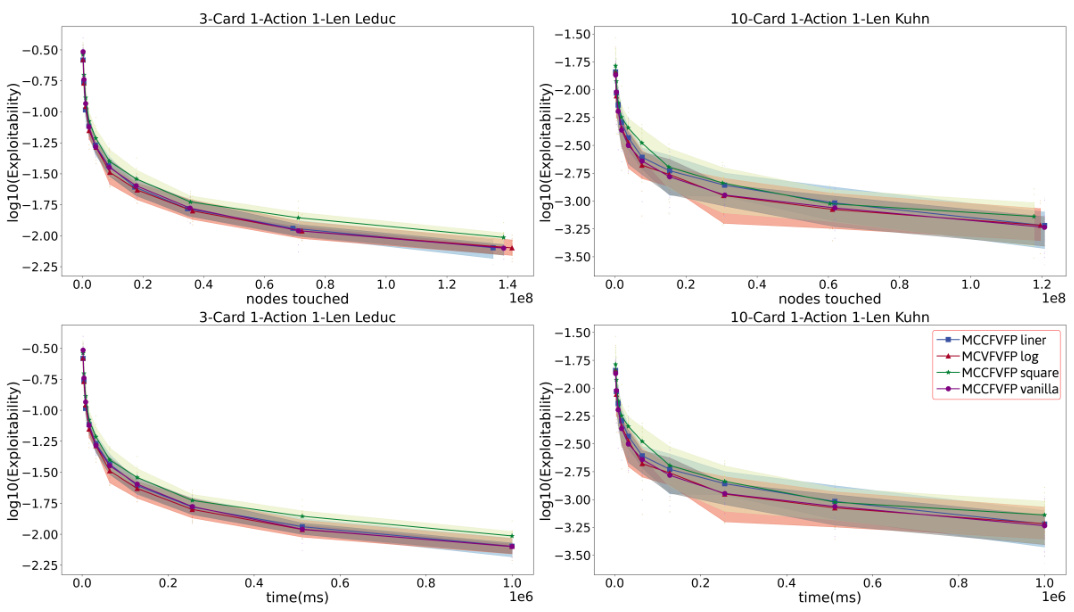
This figure compares the convergence speed of four different variants of the MCCFVFP algorithm across two different games: 3-Card 1-Action 1-Len Leduc and 10-Card 1-Action 1-Len Kuhn. The x-axis represents either the number of nodes touched or the training time (in milliseconds), and the y-axis represents the log10 of the exploitability. The lines show the average convergence behavior for each variant, with shaded areas representing confidence intervals. The purpose is to demonstrate the effectiveness of different MCCFVFP variants, showing that MCCFVFP+ generally converges faster than the others.
This figure compares the convergence speed of different algorithms (CFR, CFR+, DCFR, PCFR, MCCFR, and MCCFVFP) across various game types (Kuhn poker, Leduc poker, and Princess-and-Monster game). The top two rows show the exploitability (a measure of how far from the Nash equilibrium the strategies are) plotted against training time (in milliseconds), while the bottom two rows use the number of nodes touched as the x-axis instead. The shaded regions represent 90% confidence intervals, indicating the uncertainty in the measurements. The results illustrate how MCCFVFP consistently outperforms other algorithms, especially in larger games.
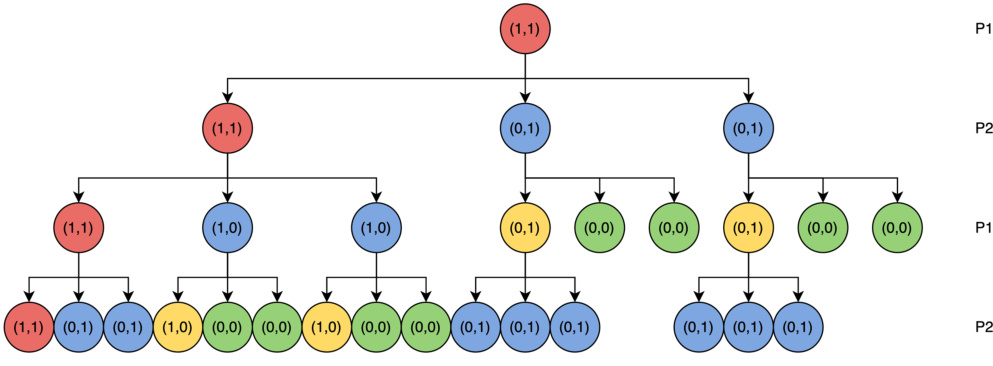
This figure shows a game tree where each node has 4 levels and 3 possible actions. The values (π¹(s), π²(s)) associated with each node represent the probability of player 1 and player 2 respectively reaching that specific node in the game. The tree visually depicts the branching possibilities and probabilities within the game’s progression.
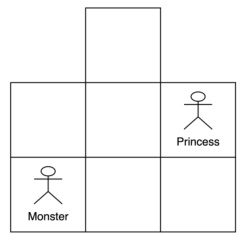
This figure illustrates the game board for the Princess and Monster game. It’s a 3x3 grid representing rooms in a dungeon. The upper-left and upper-right corners are inaccessible (blocked). The Princess and Monster are represented by stick figures and start in specific locations at the beginning of the game.
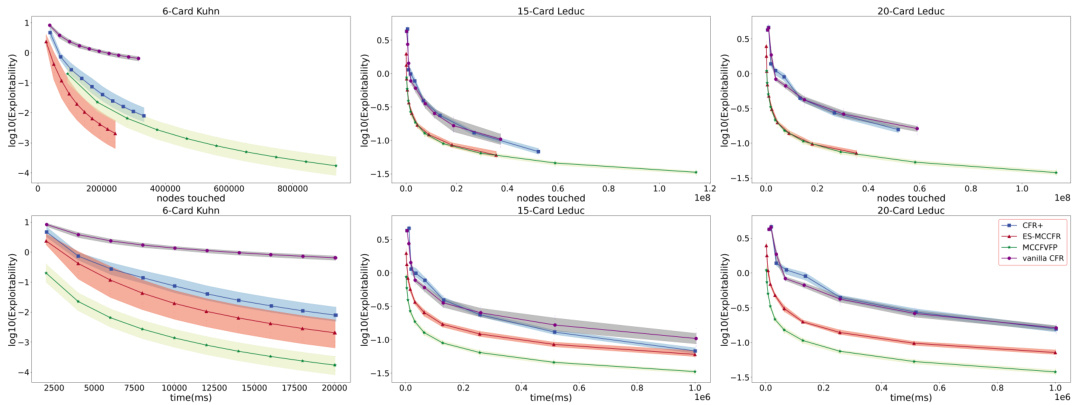
This figure compares the convergence speed of different algorithms (CFR+, ES-MCCFR, MCCFVFP, and vanilla CFR) across three different game types: Kuhn-extension poker, Leduc-extension poker, and the princess-and-monster game. The results are shown using two different metrics: training time (in milliseconds) and the number of nodes touched. The shaded regions represent the 90% confidence intervals, indicating the variability in the results. The figure demonstrates that MCCFVFP generally outperforms other algorithms in terms of convergence speed, especially as the game size increases.
More on tables
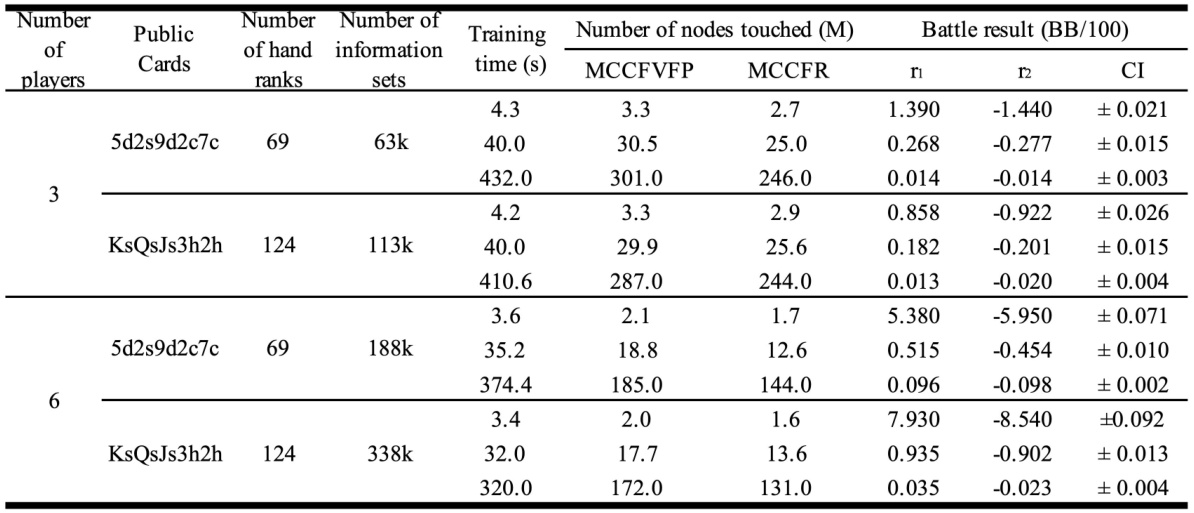
This table presents the results of multiple AI agents competing against each other in multiplayer game scenarios. It shows the training time, number of nodes touched (in millions), and battle results (in BB/100) for both MCCFVFP and MCCFR AI agents in different game configurations with varying numbers of players (3 and 6 players) and different public cards. The battle result shows the average winnings (in BB/100) of the AI, with confidence intervals to indicate the statistical significance of the results.
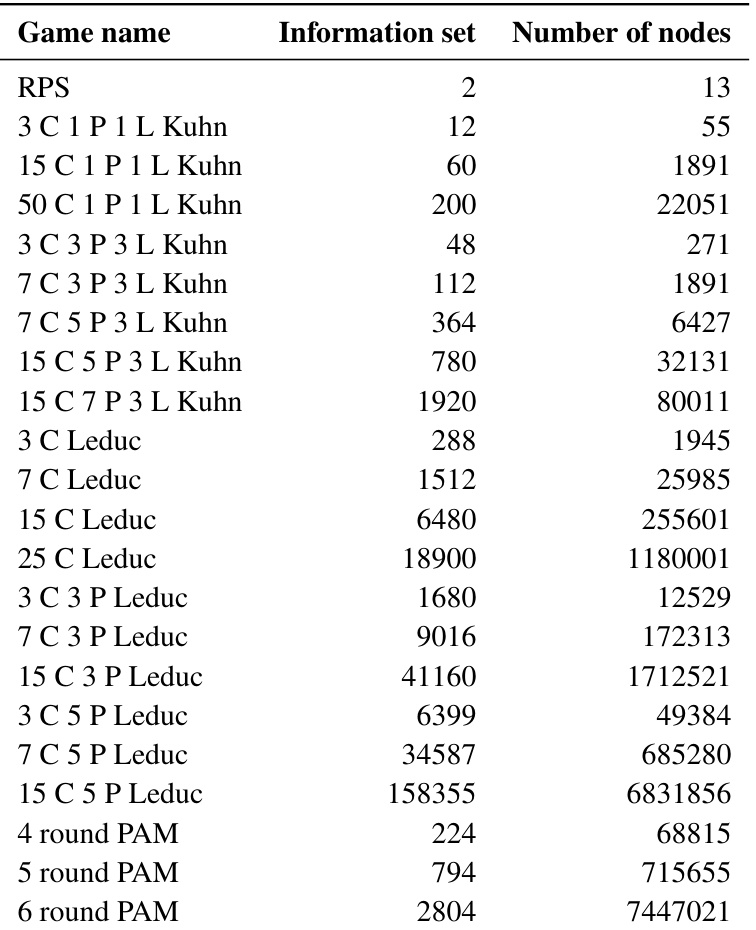
This table presents the number of information sets and nodes for various game configurations used in the experiments. The games include different variations of Kuhn poker and Leduc poker, with varying numbers of cards, actions, and raising rounds. It also includes the Princess and Monster game with different board sizes. This data showcases the complexity of the games and helps to explain the computational demands of different game scales.
Full paper#