TL;DR#
Fine-tuning large language models (LLMs) is computationally expensive. Existing methods like Low-Rank Adaptation (LoRA) offer improvements but struggle with complex tasks. These methods rely on low-rank approximations, which can limit their ability to capture all necessary task-specific information, leading to performance bottlenecks.
QuanTA uses tensor operations inspired by quantum circuits to achieve efficient high-rank fine-tuning. This allows it to effectively adapt LLMs to downstream tasks without relying on low-rank approximations. QuanTA demonstrates significant improvements over existing methods in various reasoning tasks, achieving comparable or better results with far fewer trainable parameters. It introduces no inference overhead, making it highly practical for real-world applications.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on efficient fine-tuning methods for large language models. It introduces QuanTA, a novel method that outperforms existing techniques while using significantly fewer parameters. This opens avenues for more efficient and scalable LLM adaptation, addressing a major bottleneck in the field and facilitating wider adoption of LLMs in resource-constrained settings. The theoretical underpinnings and empirical results will greatly aid research into parameter-efficient fine-tuning.
Visual Insights#
🔼 This figure compares QuanTA and LoRA, two methods for fine-tuning large language models. LoRA uses low-rank matrices to update model weights, limiting its ability to capture complex relationships. QuanTA, inspired by quantum circuits, uses tensors to update weights along specific axes. This allows for high-rank updates, improving performance while using fewer parameters. The graph illustrates that QuanTA achieves performance closer to full fine-tuning than LoRA.
read the caption
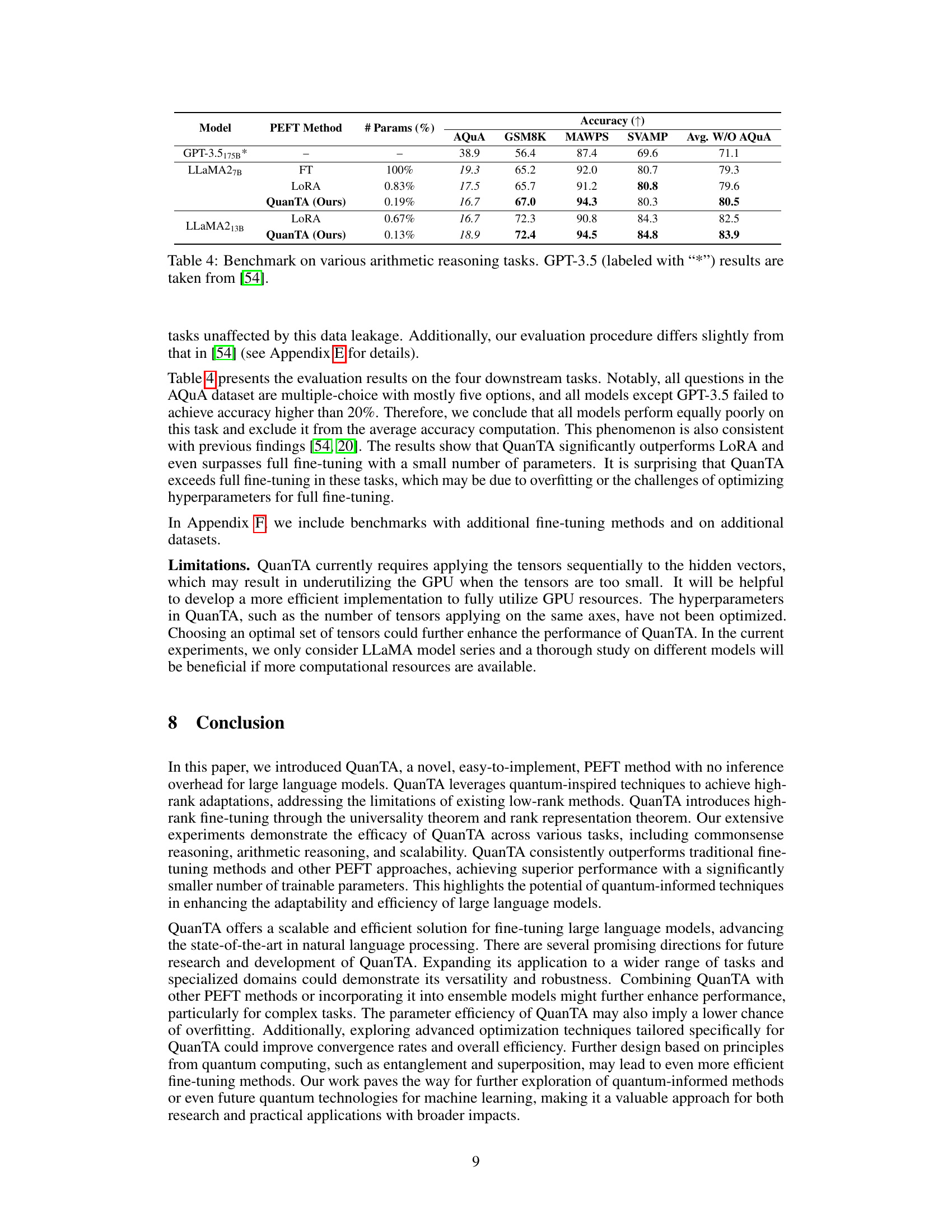
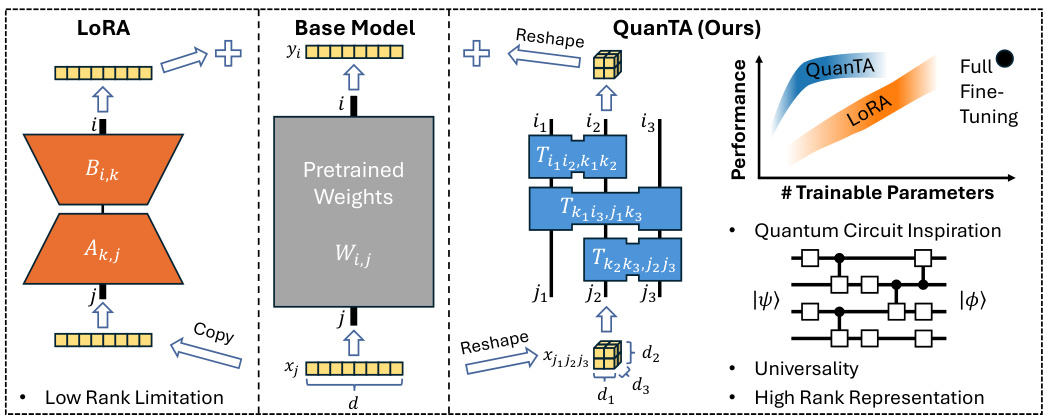
Figure 1: Conceptual comparison of QuanTA and LoRA methods. LoRA parameterizes the weight matrix update as a outer product of two low-rank matrices, limiting its capacity. QuanTA, inspired by quantum circuits, uses tensors that operate on specific axes of the (reshaped) input, enabling high-rank parameterization. Supported by the universality theorem and rank representation theorem, QuanTA can represent arbitrary matrices effectively, allowing it to achieve performance comparable to or sometimes even better than full fine-tuning, with only a fraction of the parameters. Note: the performance graph is a conceptual illustration.
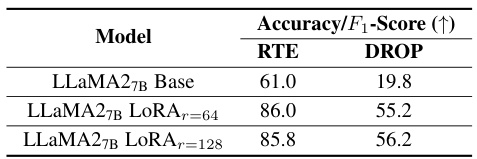
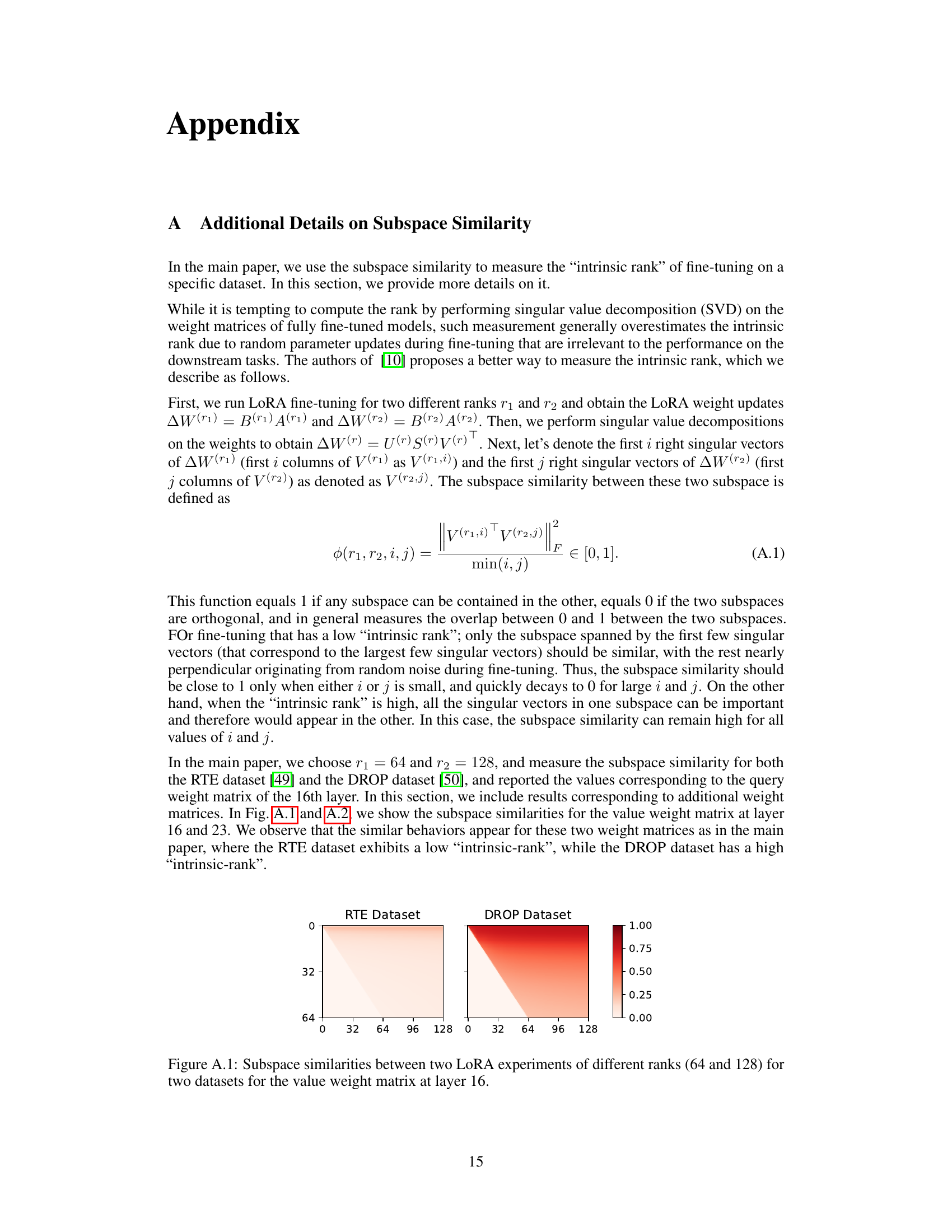
🔼 This table presents the performance comparison of the base LLaMA2-7B model and the same model fine-tuned using LoRA with rank 64 and 128 on two different datasets: RTE and DROP. RTE (Recognizing Textual Entailment) is a simpler classification task, while DROP (Difficult Reasoning Over Paragraphs) is a more complex generation task. The table shows that LoRA improves performance on both datasets, but the improvement is more significant on the RTE dataset. This suggests that the low-rank assumption of LoRA might not hold as well for complex tasks such as DROP.
read the caption
Table 1: Performance of base and LoRA fine-tuned LLaMA2-7B on RTE [49] and DROP [50] datasets. We use accuracy and F₁-score as the metrics for them respectively.
In-depth insights#
Quantum-inspired LLM Tuning#
Quantum-inspired large language model (LLM) tuning represents a novel approach to enhance the efficiency and effectiveness of fine-tuning these massive models. By drawing inspiration from quantum computing principles, methods such as QuanTA aim to overcome the limitations of existing low-rank adaptation techniques. Instead of low-rank approximations, which can hinder performance on complex tasks, these quantum-inspired methods enable efficient high-rank fine-tuning. This approach is theoretically supported by the universality and rank representation theorems, demonstrating its capability to capture intricate task-specific patterns. The use of tensor operations analogous to quantum circuits facilitates efficient high-rank parameterization, significantly reducing the number of trainable parameters while maintaining or even surpassing the performance of full fine-tuning. Furthermore, quantum-inspired tuning methods generally avoid any inference overhead, making them particularly attractive for large-scale deployment. However, the field is still nascent, and several challenges remain such as optimizing the number of tensors and achieving efficient GPU utilization. Further research is needed to fully explore the potential and address the limitations of this promising area.
High-Rank Tensor Adaptation#
High-rank tensor adaptation emerges as a powerful technique to overcome limitations in parameter-efficient fine-tuning of large language models (LLMs). Traditional low-rank methods, while efficient, often fall short on complex tasks due to their inherent inability to capture the full complexity of high-dimensional weight updates. High-rank approaches, in contrast, offer greater expressiveness and flexibility by directly addressing the high-rank nature of these updates. This enhanced representational power allows for significantly improved performance on challenging downstream tasks, exceeding what is achievable with low-rank approximations. However, the increased number of parameters associated with high-rank methods may raise concerns about computational cost. Therefore, the core challenge lies in developing techniques that achieve high-rank adaptation without sacrificing efficiency. Quantum-inspired methods, leveraging tensor operations analogous to quantum circuits, provide a promising solution. By cleverly parameterizing weight updates with a small set of tensors, these methods enable high-rank representation while maintaining manageable computational burdens. This approach represents a significant advance in parameter-efficient fine-tuning, offering a robust and scalable solution for adapting LLMs to diverse applications.
QuanTA: Method & Results#
The QuanTA method, inspired by quantum circuit structures, introduces a novel parameter-efficient fine-tuning approach for LLMs. Unlike low-rank adaptation methods (e.g., LoRA), QuanTA facilitates efficient high-rank fine-tuning, addressing limitations in representing complex downstream tasks. This is theoretically supported by the universality and rank representation theorems. Empirically, QuanTA demonstrates significant performance gains across various reasoning tasks (commonsense, arithmetic), outperforming LoRA and often matching or exceeding full fine-tuning performance with far fewer trainable parameters. The method’s ease of implementation and absence of inference overhead are key advantages. QuanTA’s scalability is highlighted by its superior performance even on large LLMs. However, potential limitations regarding optimal tensor configurations and GPU utilization efficiency during training warrant further investigation.
Low-Rank Limits Challenged#
The heading ‘Low-Rank Limits Challenged’ aptly encapsulates a central theme in the paper, focusing on the limitations of low-rank adaptation (LoRA) methods for fine-tuning large language models (LLMs). The authors argue that LoRA’s reliance on low-rank approximations restricts its ability to capture the complexities of certain downstream tasks, leading to suboptimal performance. This limitation is particularly evident when dealing with intricate tasks that deviate significantly from the pre-training data. The paper posits that this low-rank constraint hinders the model’s capacity to learn the necessary task-specific adaptations, highlighting the need for more expressive high-rank methods. This challenge forms the core motivation for proposing QuanTA, a novel quantum-inspired technique that overcomes LoRA’s limitations by facilitating efficient high-rank fine-tuning without sacrificing computational efficiency. QuanTA’s superior performance across diverse tasks serves as direct evidence that the low-rank assumption inherent to LoRA is not universally sufficient for achieving state-of-the-art results in LLM adaptation.
Future QuanTA Directions#
Future research could explore several promising avenues to enhance QuanTA. Improving efficiency is crucial, potentially by optimizing tensor application order or developing specialized hardware acceleration. Generalizing QuanTA to diverse model architectures and leveraging other parameter-efficient fine-tuning methods (like prefix-tuning or adapters) in a hybrid approach are key directions. Theoretical investigations could delve deeper into the rank representation theorem to improve its applicability to complex tasks and further explore the connection between QuanTA’s quantum-inspired structure and its empirical performance. Addressing limitations in handling very large models and optimizing hyperparameters is crucial for widespread adoption. Finally, exploring advanced optimization techniques specifically designed for QuanTA’s unique structure could unlock even greater performance gains, paving the way for future applications in diverse areas.
More visual insights#
More on figures
🔼 This figure conceptually compares QuanTA and LoRA methods for parameter-efficient fine-tuning of LLMs. LoRA uses low-rank matrix updates, limiting its representational capacity. QuanTA, drawing inspiration from quantum circuits, employs tensors operating on specific input axes, enabling higher-rank parameterizations. Theoretically, QuanTA’s ability to represent arbitrary matrices effectively is supported by the universality theorem and the rank representation theorem, promising performance comparable to or exceeding full fine-tuning with significantly fewer parameters.
read the caption
Figure 1: Conceptual comparison of QuanTA and LoRA methods. LoRA parameterizes the weight matrix update as a outer product of two low-rank matrices, limiting its capacity. QuanTA, inspired by quantum circuits, uses tensors that operate on specific axes of the (reshaped) input, enabling high-rank parameterization. Supported by the universality theorem and rank representation theorem, QuanTA can represent arbitrary matrices effectively, allowing it to achieve performance comparable to or sometimes even better than full fine-tuning, with only a fraction of the parameters. Note: the performance graph is a conceptual illustration.
🔼 This figure illustrates the universality of quantum circuits. It shows that any unitary matrix (a type of mathematical transformation representing a quantum operation) can be broken down into a sequence of simpler operations, namely single-qubit and two-qubit gates. This decomposition is crucial because it demonstrates that complex quantum computations can be constructed from a limited set of basic building blocks. This concept is foundational to the development of QuanTA, as it demonstrates that high-rank operations can be achieved using a composition of smaller operations.
read the caption
Figure 3: Any unitary matrix can be decomposed into a quantum circuit using one- and two-qubit gates.

🔼 This figure compares QuanTA and LoRA, two parameter-efficient fine-tuning methods for LLMs. LoRA uses low-rank matrix updates, limiting its ability to capture complex relationships in data. QuanTA, inspired by quantum circuits, uses tensor operations on specific axes of the input, allowing for high-rank updates. This enables QuanTA to represent a wider range of matrices than LoRA, leading to performance closer to or even surpassing full fine-tuning, but with far fewer parameters.
read the caption
Figure 1: Conceptual comparison of QuanTA and LoRA methods. LoRA parameterizes the weight matrix update as a outer product of two low-rank matrices, limiting its capacity. QuanTA, inspired by quantum circuits, uses tensors that operate on specific axes of the (reshaped) input, enabling high-rank parameterization. Supported by the universality theorem and rank representation theorem, QuanTA can represent arbitrary matrices effectively, allowing it to achieve performance comparable to or sometimes even better than full fine-tuning, with only a fraction of the parameters. Note: the performance graph is a conceptual illustration.

🔼 This figure compares QuanTA and LoRA methods. LoRA uses low-rank matrices to update weight matrices, limiting its capacity to handle complex tasks. QuanTA, inspired by quantum circuits, employs tensors operating on specific input axes, allowing for high-rank parameterization. Theoretically, QuanTA can represent arbitrary matrices efficiently, potentially outperforming full fine-tuning with fewer parameters.
read the caption
Figure 1: Conceptual comparison of QuanTA and LoRA methods. LoRA parameterizes the weight matrix update as a outer product of two low-rank matrices, limiting its capacity. QuanTA, inspired by quantum circuits, uses tensors that operate on specific axes of the (reshaped) input, enabling high-rank parameterization. Supported by the universality theorem and rank representation theorem, QuanTA can represent arbitrary matrices effectively, allowing it to achieve performance comparable to or sometimes even better than full fine-tuning, with only a fraction of the parameters. Note: the performance graph is a conceptual illustration.

🔼 This figure conceptually compares QuanTA and LoRA, highlighting their differences in parameterizing weight matrix updates. LoRA uses low-rank matrices, limiting its representational capacity, while QuanTA leverages tensors inspired by quantum circuits for high-rank parameterization, enabling more expressive updates and better performance with fewer parameters. The universality and rank representation theorems underpin QuanTA’s ability to efficiently represent arbitrary matrices.
read the caption
Figure 1: Conceptual comparison of QuanTA and LoRA methods. LoRA parameterizes the weight matrix update as a outer product of two low-rank matrices, limiting its capacity. QuanTA, inspired by quantum circuits, uses tensors that operate on specific axes of the (reshaped) input, enabling high-rank parameterization. Supported by the universality theorem and rank representation theorem, QuanTA can represent arbitrary matrices effectively, allowing it to achieve performance comparable to or sometimes even better than full fine-tuning, with only a fraction of the parameters. Note: the performance graph is a conceptual illustration.
🔼 The figure conceptually compares QuanTA and LoRA methods for fine-tuning LLMs. LoRA uses low-rank matrix updates, limiting its ability to capture complex relationships. QuanTA, inspired by quantum circuits, uses tensors for high-rank updates, enabling more flexible adaptation and potentially better performance with fewer parameters.
read the caption
Figure 1: Conceptual comparison of QuanTA and LoRA methods. LoRA parameterizes the weight matrix update as a outer product of two low-rank matrices, limiting its capacity. QuanTA, inspired by quantum circuits, uses tensors that operate on specific axes of the (reshaped) input, enabling high-rank parameterization. Supported by the universality theorem and rank representation theorem, QuanTA can represent arbitrary matrices effectively, allowing it to achieve performance comparable to or sometimes even better than full fine-tuning, with only a fraction of the parameters. Note: the performance graph is a conceptual illustration.

🔼 The figure conceptually compares QuanTA and LoRA, highlighting their differences in how they parameterize weight matrix updates. LoRA uses low-rank matrices, limiting its capacity to capture complex relationships. In contrast, QuanTA uses tensors inspired by quantum circuits to enable high-rank parameterization, allowing it to effectively represent arbitrary matrices and potentially achieve superior performance while using fewer parameters.
read the caption
Figure 1: Conceptual comparison of QuanTA and LoRA methods. LoRA parameterizes the weight matrix update as a outer product of two low-rank matrices, limiting its capacity. QuanTA, inspired by quantum circuits, uses tensors that operate on specific axes of the (reshaped) input, enabling high-rank parameterization. Supported by the universality theorem and rank representation theorem, QuanTA can represent arbitrary matrices effectively, allowing it to achieve performance comparable to or sometimes even better than full fine-tuning, with only a fraction of the parameters. Note: the performance graph is a conceptual illustration.
More on tables
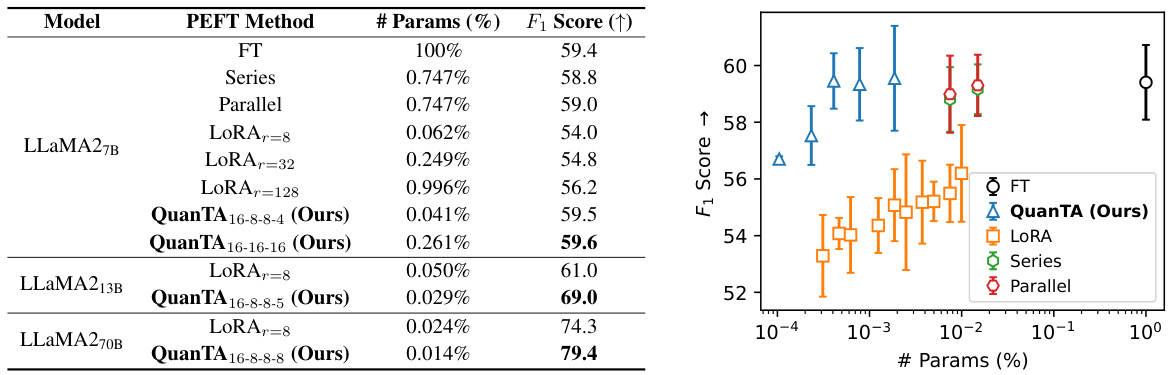
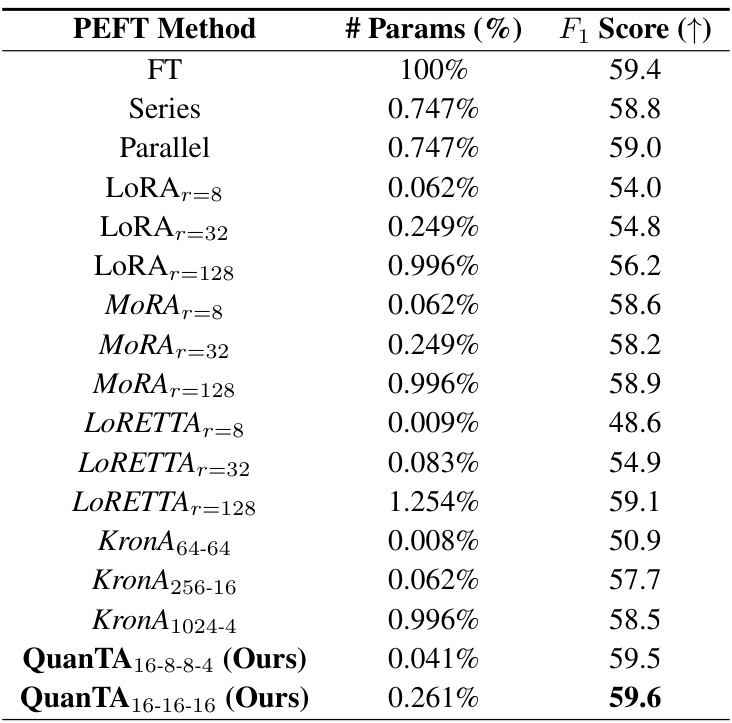
🔼 This table compares the performance of several parameter-efficient fine-tuning (PEFT) methods on the DROP dataset, using different sizes of the LLaMA2 language model. The methods compared include full fine-tuning (FT), series adapters, parallel adapters, LoRA with different ranks, and QuanTA with different parameter configurations. The table shows the number of trainable parameters used by each method (as a percentage of the total parameters) and the resulting F1 score achieved. The results highlight QuanTA’s superior performance compared to other PEFT methods, especially when using a small fraction of trainable parameters.
read the caption
Table 2: Benchmark of various fine-tuning methods on the DROP dataset using LLaMA2 7-70 billion parameter models as the base model. In each case, we report the average of F₁ score over 2-4 experiments with different random seeds.

🔼 This table compares the performance of various parameter-efficient fine-tuning (PEFT) methods on several commonsense reasoning tasks using different sized language models (LLaMAs). It shows the accuracy achieved by different methods (Full Fine-tuning, Prefix Tuning, Adapter methods, LoRA, DORA, and QuanTA) with varying numbers of trainable parameters. The results demonstrate QuanTA’s superior performance and efficiency compared to other PEFT methods.
read the caption
Table 3: Benchmark on various commonsense reasoning tasks. All results of models and PEFT methods labeled with “*” are from [54], and results with “†” are from [20].
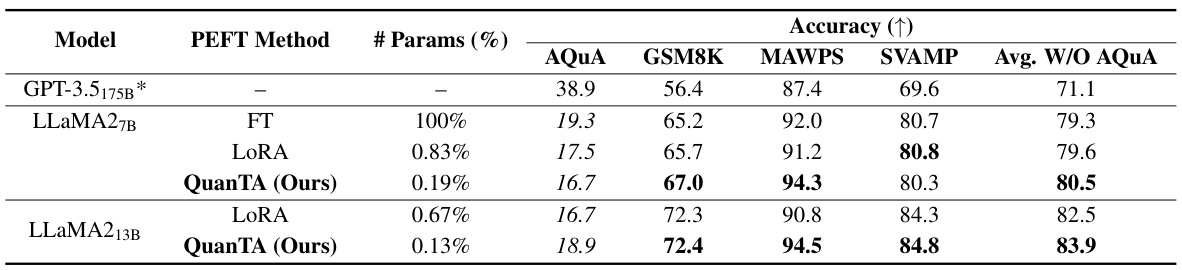
🔼 This table presents the results of several models on four arithmetic reasoning tasks. The models tested include LLaMA2-7B and LLaMA2-13B, fine-tuned with different parameter-efficient fine-tuning (PEFT) methods such as full fine-tuning (FT), LoRA, and QuanTA. The table compares the accuracy of each model and method across the four tasks. The results show that QuanTA consistently outperforms LoRA and often surpasses full fine-tuning, particularly on the MAWPS and SVAMP datasets, while using a significantly smaller number of parameters.
read the caption
Table 4: Benchmark on various arithmetic reasoning tasks. GPT-3.5 (labeled with *) results are taken from [54].
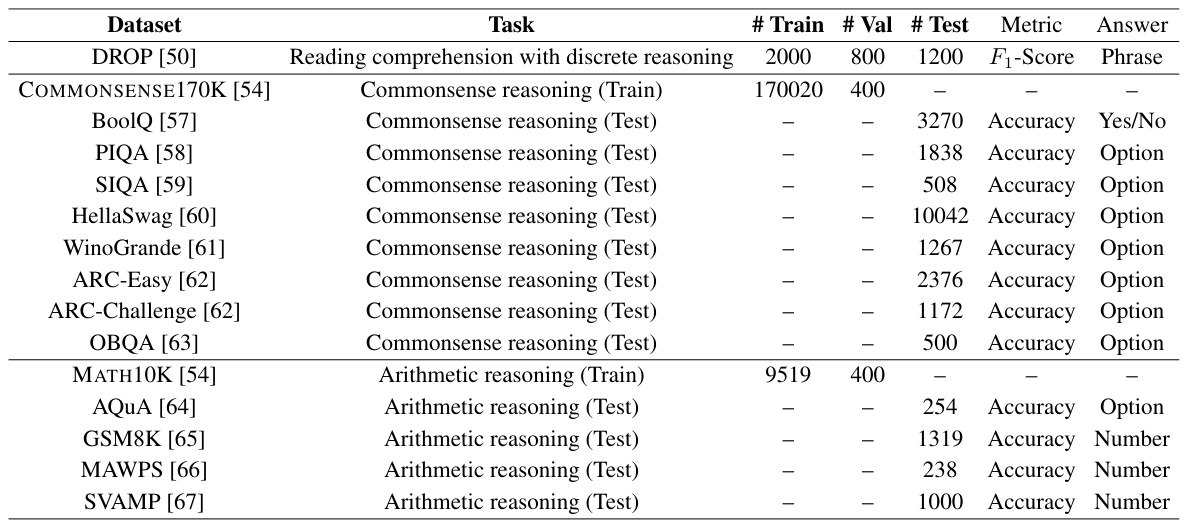
🔼 This table lists all the datasets used in the QuanTA paper, specifying the dataset name, the task it was used for (reading comprehension, commonsense reasoning, or arithmetic reasoning), and the number of training, validation, and test samples for each. The table also indicates the evaluation metric (F₁-score or accuracy) and the type of answer expected (phrase, yes/no, option, or number).
read the caption
Table D.1: List of datasets used in this work.

🔼 This table compares the performance of several parameter-efficient fine-tuning (PEFT) methods on the DROP dataset, using different sizes of the LLaMA2 model as a base. It shows the number of trainable parameters used by each method (as a percentage of the total parameters), and the resulting F1 score. The methods compared include full fine-tuning, series adapters, parallel adapters, LoRA with different ranks, and QuanTA with different configurations. The table highlights QuanTA’s ability to achieve high F1 scores with significantly fewer trainable parameters compared to other methods.
read the caption
Table 2: Benchmark of various fine-tuning methods on the DROP dataset using LLaMA2 7-70 billion parameter models as the base model. In each case, we report the average of F₁ score over 2-4 experiments with different random seeds.
🔼 This table compares different parameter-efficient fine-tuning (PEFT) methods on the DROP dataset using LLaMA2 models with varying parameter counts (7B and 70B). The methods include full fine-tuning (FT), series and parallel adapters, LoRA with different ranks, and QuanTA with different configurations. The performance metric is the F1 score, averaged across multiple experiments with different random seeds to account for variability.
read the caption
Table 2: Benchmark of various fine-tuning methods on the DROP dataset using LLaMA2 7-70 billion parameter models as the base model. In each case, we report the average of F₁ score over 2-4 experiments with different random seeds.
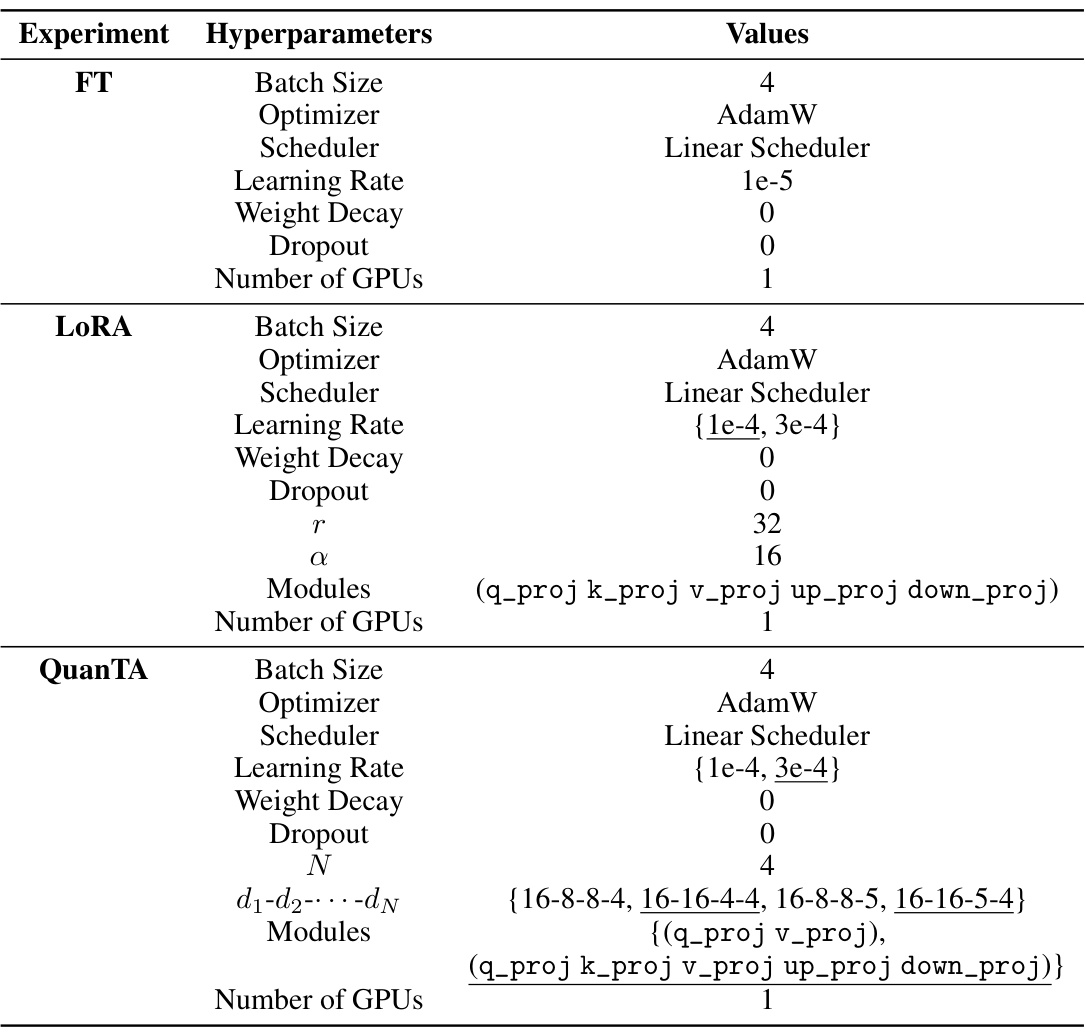
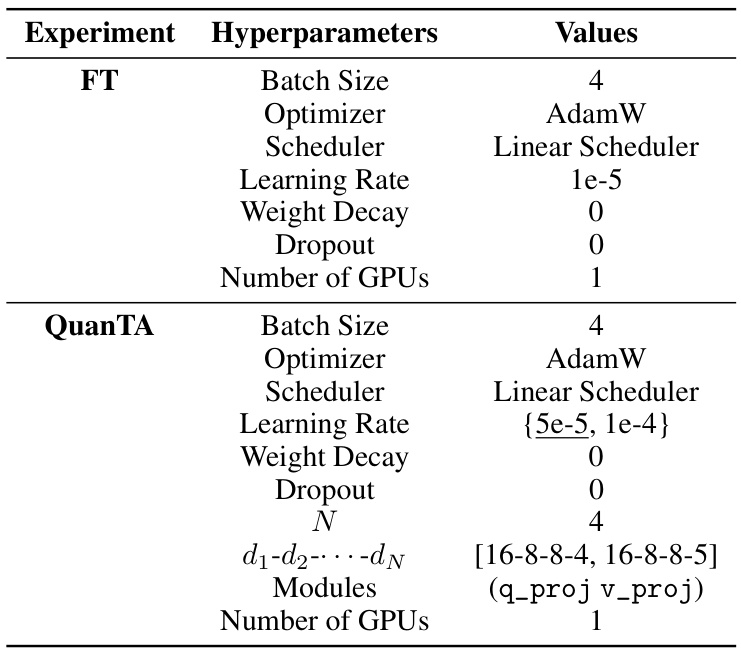
🔼 This table lists the hyperparameters used in the experiments for the DROP dataset. It shows the values used for each of the different fine-tuning methods (Full Fine-tuning (FT), Series Adapters, Parallel Adapters, LoRA, and QuanTA). Curly brackets indicate the range of hyperparameters tested during optimization, while the underscored values are the ones finally selected. Square brackets show hyperparameter variations used in different experiments reported in the main paper. The table provides a detailed breakdown of the settings used for each method, aiding in reproducibility and understanding of the experimental setup.
read the caption
Table E.2: Hyperparameters used for DROP dataset for various fine-tuning methods. Curly brackets include the hyperparameter values tested during hyperparameter optimization, with the actual hyperparameter(s) underscored. Square brackets include hyperparameter values for different experiments conducted in the main paper.
🔼 This table compares the performance of different parameter-efficient fine-tuning (PEFT) methods on the DROP dataset, using LLaMA2 models with varying parameter counts. It shows the F1 score achieved by each method, along with the percentage of parameters used relative to full fine-tuning. The goal is to demonstrate QuanTA’s efficiency and effectiveness compared to other techniques like LoRA and adapter-based methods.
read the caption
Table 2: Benchmark of various fine-tuning methods on the DROP dataset using LLaMA2 7-70 billion parameter models as the base model. In each case, we report the average of F₁ score over 2-4 experiments with different random seeds.

🔼 This table compares the performance of different parameter-efficient fine-tuning (PEFT) methods on various commonsense reasoning tasks. The results are shown as accuracy scores for several benchmark datasets (BoolQ, PIQA, SIQA, Hellaswag, Winograd Schema Challenge, ARC-e, ARC-c, and OBQA). The table highlights the performance of QuanTA against other PEFT methods such as full fine-tuning (FT), LoRA, DORA, and adapter-based methods (Series and Parallel). The ‘#Params (%) column shows the percentage of parameters trained for each method relative to the full fine-tuning approach. Some results are sourced from external studies [54, 20].
read the caption
Table 3: Benchmark on various commonsense reasoning tasks. All results of models and PEFT methods labeled with “*” are from [54], and results with “†” are from [20].

🔼 This table presents the results of benchmarking various parameter-efficient fine-tuning (PEFT) methods on five natural language understanding tasks from the GLUE benchmark, using the RoBERTa model as the base. It compares the performance of LoRA and QuanTA (the proposed method) in terms of accuracy on SST-2, MRPC, CoLA, RTE, and STS-B tasks. The table highlights the number of trainable parameters used by each method as a percentage of the total model parameters.
read the caption
Table F.7: Benchmark on five natural language understanding tasks using RoBERTa model as the base model.
Full paper#