↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many fairness-aware meta-learning algorithms struggle with hypergradient conflicts, leading to unstable convergence and suboptimal fairness. These conflicts arise when multiple fairness objectives are incorporated via meta-learning; the overall gradient might not align with the best updates for all subgroups, resulting in unstable model performance and potentially unfair results. This paper tackles this challenge head-on.
The proposed solution is a two-stage meta-learning framework that leverages the Nash Bargaining Solution (NBS) to resolve these conflicts. The first stage uses NBS to find a solution that steers the model towards the Pareto front, achieving a balance between different fairness goals. The second stage further optimizes the model based on specific fairness objectives. The approach is supported by theoretical results, demonstrating Pareto improvement and monotonic improvement in validation loss. Experiments on various benchmark datasets highlight its efficacy in improving both performance and fairness compared to existing one-stage methods.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on fairness-aware machine learning. It introduces a novel two-stage meta-learning framework that effectively addresses hypergradient conflicts, a major challenge in existing methods. The theoretical underpinnings and empirical results demonstrate its efficacy in improving both model performance and fairness across various datasets and tasks. This opens up new avenues for research in the design of fair and effective algorithms.
Visual Insights#

The figure illustrates the problem of hypergradient conflicts in one-stage fairness-aware meta-learning and proposes a two-stage solution. The left panel shows different conflict scenarios, while the right panel compares the performance of the proposed two-stage method with a conventional one-stage method, demonstrating significant improvements in both performance and fairness.

This table compares the performance of three conventional one-stage meta-learning methods (LtR, FORML, and Meta-gDRO) and the proposed two-stage Nash-Meta-Learning method on six standard fairness datasets. The performance is measured using three fairness metrics: Overall AUC (higher is better), Max-gAUCD (lower is better), and Worst-gAUC (higher is better). The table highlights the best performance for each metric across the different methods. The results show that the two-stage method generally outperforms the one-stage methods.
In-depth insights#
Nash Bargaining#
The concept of ‘Nash Bargaining’ in the context of fairness-aware meta-learning offers a novel approach to resolving conflicts between different fairness objectives. Instead of naively aggregating often-conflicting gradients from various subgroups, the authors frame the problem as a cooperative bargaining game. This innovative framework uses the Nash Bargaining Solution (NBS) to find a Pareto optimal solution, a point where no single group’s fairness can be improved without harming another. The NBS elegantly balances competing fairness goals, avoiding unstable convergence and compromised model performance often seen in simpler aggregation methods. The theoretical contributions underpinning this approach are particularly noteworthy, including a proof of the NBS free from linear independence assumptions, demonstrating its broader applicability. The two-stage framework, first resolving conflicts via NBS and then optimizing specific fairness goals, showcases the practical effectiveness of this game-theoretic approach for enhancing both model fairness and performance. This methodology offers a significant advancement in fairness-aware meta-learning, providing a robust and principled solution for a challenging problem.
Hypergradient Conflicts#
The concept of “Hypergradient Conflicts” in the context of fairness-aware meta-learning highlights a critical challenge in aligning multiple fairness objectives during model training. Standard meta-learning approaches often aggregate fairness gradients naively, leading to conflicts where optimizing for one subgroup’s fairness harms another’s. This results in unstable convergence and suboptimal model performance across subgroups. The core issue is that the aggregated gradient (hypergradient) may pull the model in a direction that violates fairness for some subgroups, even if it improves the overall performance or fairness metric. Resolving these conflicts is crucial for achieving robust and fair models, as simply averaging or prioritizing individual fairness objectives can lead to unfair and unstable outcomes. Therefore, methods that explicitly address hypergradient conflicts through techniques like cooperative game theory are needed for effective fairness-aware meta-learning.
Two-Stage Framework#
The proposed two-stage framework offers a novel approach to fairness-aware meta-learning by addressing the challenge of hypergradient conflicts. The first stage leverages the Nash Bargaining Solution (NBS) to resolve these conflicts, guiding the model towards the Pareto front where improvements in one group’s fairness do not come at the expense of another’s. This is crucial as naive integration of fairness goals often leads to unstable convergence and compromised performance. The second stage focuses on optimizing specific fairness objectives, building upon the Pareto-improved model from stage one. This decomposition into conflict resolution and objective optimization is key to achieving stable and effective fairness-aware meta-learning. The framework is supported by theoretical results demonstrating Pareto and monotonic improvement, along with empirical evidence showcasing its effectiveness across various fairness datasets.
Empirical Results#
The empirical results section of a research paper is crucial for validating the claims and hypotheses presented. A strong empirical results section will present clear and well-organized data that convincingly demonstrates the effectiveness of the proposed methods. This involves the use of appropriate evaluation metrics, a sufficient number of experiments across varied datasets or scenarios, and a robust discussion of the findings including limitations. The results should be presented in a clear and concise manner, using tables, figures, and visualizations to effectively communicate complex data. A good results section will also address potential confounding factors and provide a comprehensive analysis of the observed effects. Ultimately, the empirical results section should serve as compelling evidence supporting the overall conclusions of the research paper, showcasing the practical impact and validity of the work.
Future Directions#
The ‘Future Directions’ section of this research paper would ideally expand on several key areas. Firstly, it should address the limitations imposed by the current validation set quality and the absence of specific sensitive attribute labels in certain subgroups, proposing solutions like incorporating fairness-aware synthetic data generation techniques or data-sifting methods to enhance model robustness. Secondly, it could explore the generalizability and scalability of the Nash Bargaining Solution (NBS) approach beyond the specific datasets used in the study, particularly investigating its performance in higher-dimensional spaces with a larger number of sensitive attributes. Extending the theoretical analysis of the two-stage framework to encompass more complex scenarios, like non-linear loss functions or non-convex optimization landscapes, would be crucial. Furthermore, future work should investigate the dynamic interplay between fairness and performance across various fairness objectives in a more comprehensive manner, potentially incorporating additional economic mechanisms and exploring the ethical implications of balancing competing fairness goals. Finally, developing more comprehensive metrics for measuring fairness and model performance in the context of highly imbalanced datasets is crucial. Addressing these points will significantly enhance the impact and applicability of this work in addressing real-world fairness challenges.
More visual insights#
More on figures
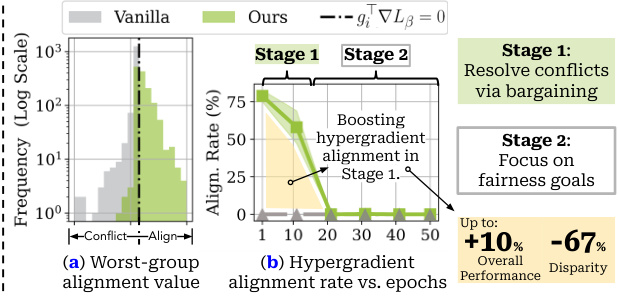
This figure illustrates the problem of hypergradient conflicts in one-stage fairness-aware meta-learning and introduces a two-stage solution. The left panel shows scenarios of conflicting and non-conflicting hypergradients, while the right panel compares a conventional one-stage approach with the proposed two-stage approach, highlighting performance and fairness improvements (up to 10% and 67%, respectively).

This figure illustrates the problem of hypergradient conflicts in one-stage fairness-aware meta-learning and introduces a two-stage solution. The left panel shows scenarios where hypergradient conflicts lead to instability and suboptimal performance. The right panel compares a conventional one-stage approach with the proposed two-stage approach which resolves the conflicts using Nash Bargaining Solution (NBS), resulting in improved performance and fairness.
This figure shows the results of synthetic experiments comparing the performance of continuous bargaining and two-stage bargaining (with bargaining only in the first 100 steps) in resolving hypergradient conflicts and converging to the Pareto front. It illustrates how the proposed two-stage approach using Nash Bargaining Solution (NBS) effectively guides the model to the Pareto front by initially resolving conflicts, thereby achieving improved fairness and performance compared to the continuous bargaining approach.

This figure illustrates the problem of hypergradient conflicts in one-stage fairness-aware meta-learning and introduces a two-stage approach to resolve them. The left panel shows different scenarios of hypergradient conflicts, while the right panel compares the performance of a conventional one-stage method and the proposed two-stage method, highlighting the improvement in both performance and fairness achieved by the latter.
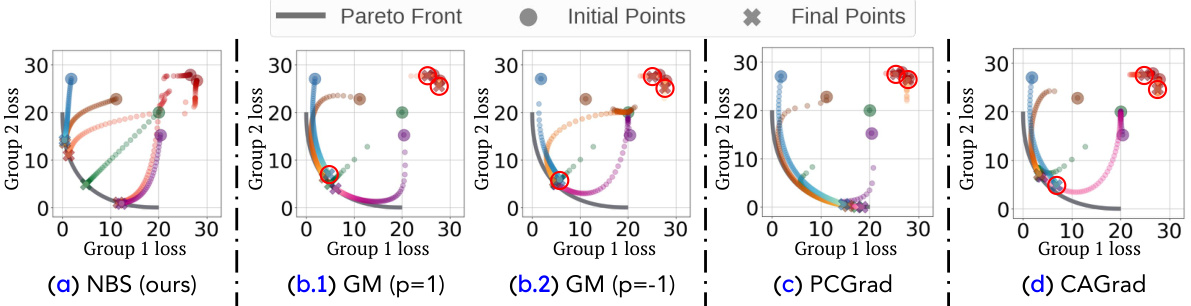
This figure compares different gradient aggregation methods’ performance in resolving hypergradient conflicts and converging to the Pareto front in a synthetic experiment. The methods compared are the Nash Bargaining Solution (NBS), Generalized Mean (GM) with p=1 and p=-1, PCGrad, and CAGrad. The plot shows the trajectory of the optimization process for multiple initial points. Red circles highlight the points that fail to reach the Pareto front after 1000 optimization steps. The figure demonstrates that the NBS effectively steers the optimization toward the Pareto front, while other methods struggle with conflicts and may get stuck in suboptimal regions.

This figure illustrates the challenges of using conventional one-stage fairness-aware meta-learning methods. It shows that these methods can lead to erratic performance and/or convergence at suboptimal, unfair local minima. Panel (a) compares the performance of three different one-stage methods across multiple fairness notions, showing inconsistent results. Panel (b) visualizes the trajectory of the optimization process for these methods, demonstrating that they often fail to reach a point that is both fair and performant. This highlights the need for a more robust approach to fairness-aware meta-learning, such as the two-stage Nash bargaining approach proposed in the paper.
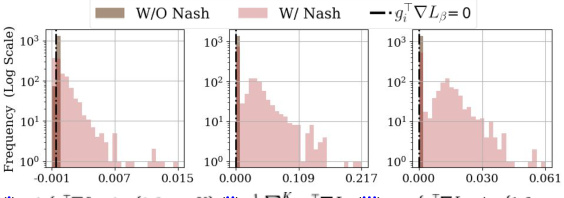
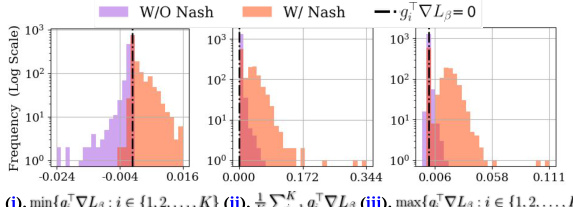
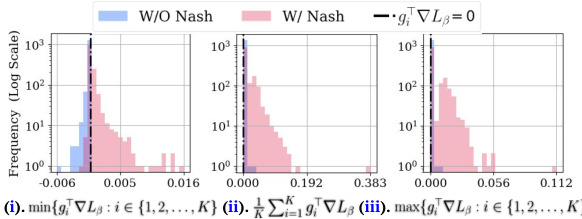
This figure shows how Nash bargaining resolves hypergradient conflicts in different one-stage fairness-aware meta-learning methods. It uses histograms to illustrate the distribution of the minimum, average, and maximum group-wise hypergradient alignment values (before and after Nash bargaining). The results show that Nash bargaining effectively resolves conflicts and improves hypergradient alignment, leading to better fairness and performance.
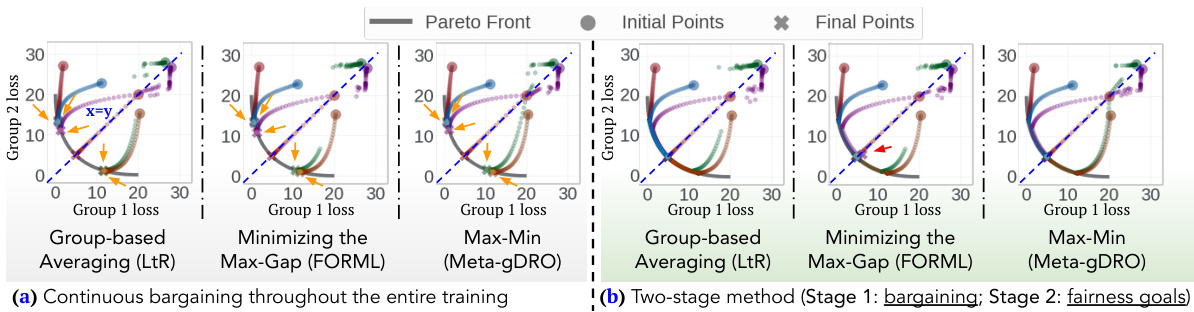
This figure illustrates the effectiveness of Nash bargaining in resolving hypergradient conflicts and guiding the model towards the Pareto front in synthetic experiments. Panel (a) shows continuous bargaining throughout the entire training process, demonstrating that the bargaining process enhances convergence to the Pareto front. Panel (b) contrasts this with the two-stage approach, where bargaining is used only in the initial stage to resolve conflicts before focusing on fairness goals, showing a similar positive impact on the model’s convergence to the Pareto front. In both cases, points far from the fairness goal (x=y) or not on the Pareto front are highlighted to show contrast and improved results from Nash bargaining.
This figure illustrates the effectiveness of Nash bargaining in resolving hypergradient conflicts and steering the model towards the Pareto front in a synthetic setting. Panel (a) shows continuous bargaining throughout the entire training process, while panel (b) demonstrates the two-stage approach where bargaining is only used in the initial steps before the model focuses on fairness goals. The results highlight that the two-stage method using Nash bargaining achieves a better convergence to the Pareto front compared to conventional one-stage methods and improves fairness and performance.

This figure shows the results of synthetic experiments comparing the performance of a conventional one-stage fairness-aware meta-learning method with a proposed two-stage method that incorporates Nash bargaining. The figure highlights how the two-stage method effectively resolves hypergradient conflicts and guides the model toward the Pareto front, leading to better fairness and performance outcomes compared to the one-stage method. Subfigure (a) shows continuous bargaining throughout the entire training process, while subfigure (b) shows bargaining only in the initial 100 steps. The results demonstrate the efficacy of resolving conflicts before focusing on specific fairness goals.
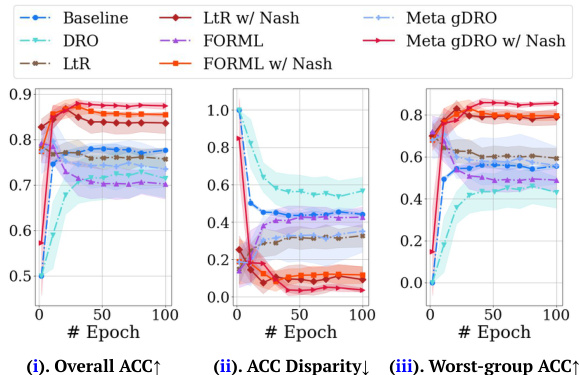
The figure shows the unreliable performance of conventional one-stage fairness-aware meta-learning methods across various fairness notions. Subfigure (a) compares the model performance of three conventional one-stage meta-learning methods (LtR, FORML, and Meta-gDRO) across various fairness notions. Subfigure (b) shows the trajectory of 1000-step optimizations for the three methods, illustrating hypergradient conflicts leading to unstable performance and convergence at suboptimal, unfair local minima.
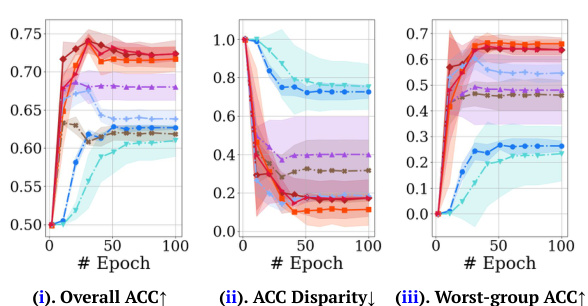
This figure shows the unreliable performance of conventional one-stage fairness-aware meta-learning methods across various fairness notions. The left panel (a) compares the average model performance of three methods (LtR, FORML, and Meta-gDRO) across various fairness notions. The results highlight instability and suboptimal performance in terms of both overall performance and fairness. The right panel (b) visualizes the optimization trajectory of these one-stage methods, showing erratic convergence and a tendency to converge to unfair local minima, rather than the desired point of equal validation loss for both groups and optimal performance, illustrated by the Pareto front.
More on tables

This table presents the performance comparison of the proposed two-stage Nash-Meta-Learning method against three conventional one-stage meta-learning methods (LtR, FORML, and Meta-gDRO) and a baseline method (DRO) across six standard fairness datasets. The results are averaged over five runs. Each method is evaluated using three fairness metrics: Overall AUC (higher is better), Max-gAUCD (lower is better), and Worst-gAUC (higher is better). The table highlights the best performing method for each dataset and metric.
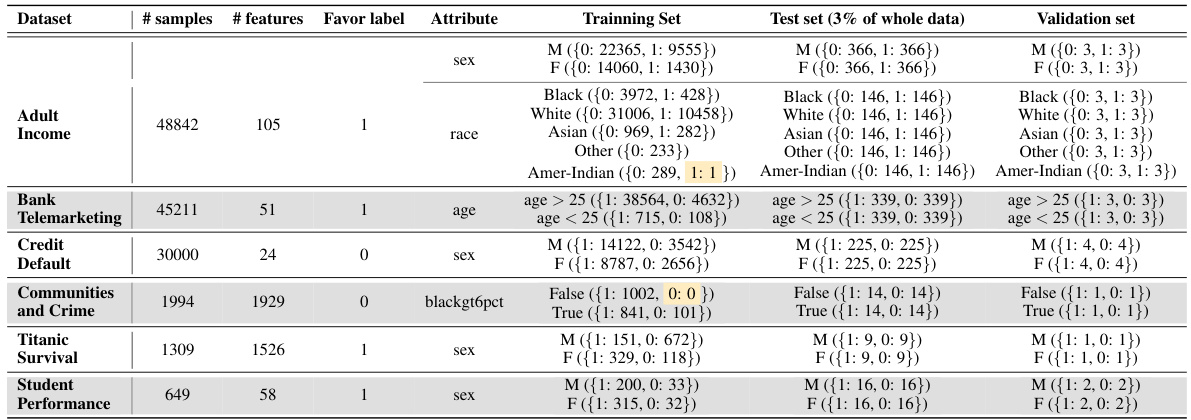
This table details the data distribution across different groups based on protected attributes and labels for six fairness datasets. It highlights imbalances in some datasets, such as the adult income dataset having only one Amer-Indian sample with a positive label, and the communities and crime dataset having no samples in the ‘False’ group after balancing the test and validation sets. This information is relevant for understanding the experimental setup and potential challenges in achieving fairness.

This table compares the performance of the proposed two-stage Nash-Meta-Learning method against three conventional one-stage meta-learning methods (LtR, FORML, Meta-gDRO) and a baseline method (DRO) across six standard fairness datasets. The performance is evaluated using three metrics: Overall AUC (higher is better, measuring overall prediction accuracy), Max-gAUCD (lower is better, measuring the maximum difference in AUC across groups), and Worst-gAUC (higher is better, measuring the AUC of the worst-performing group). The best result for each metric in each dataset is shown in bold.
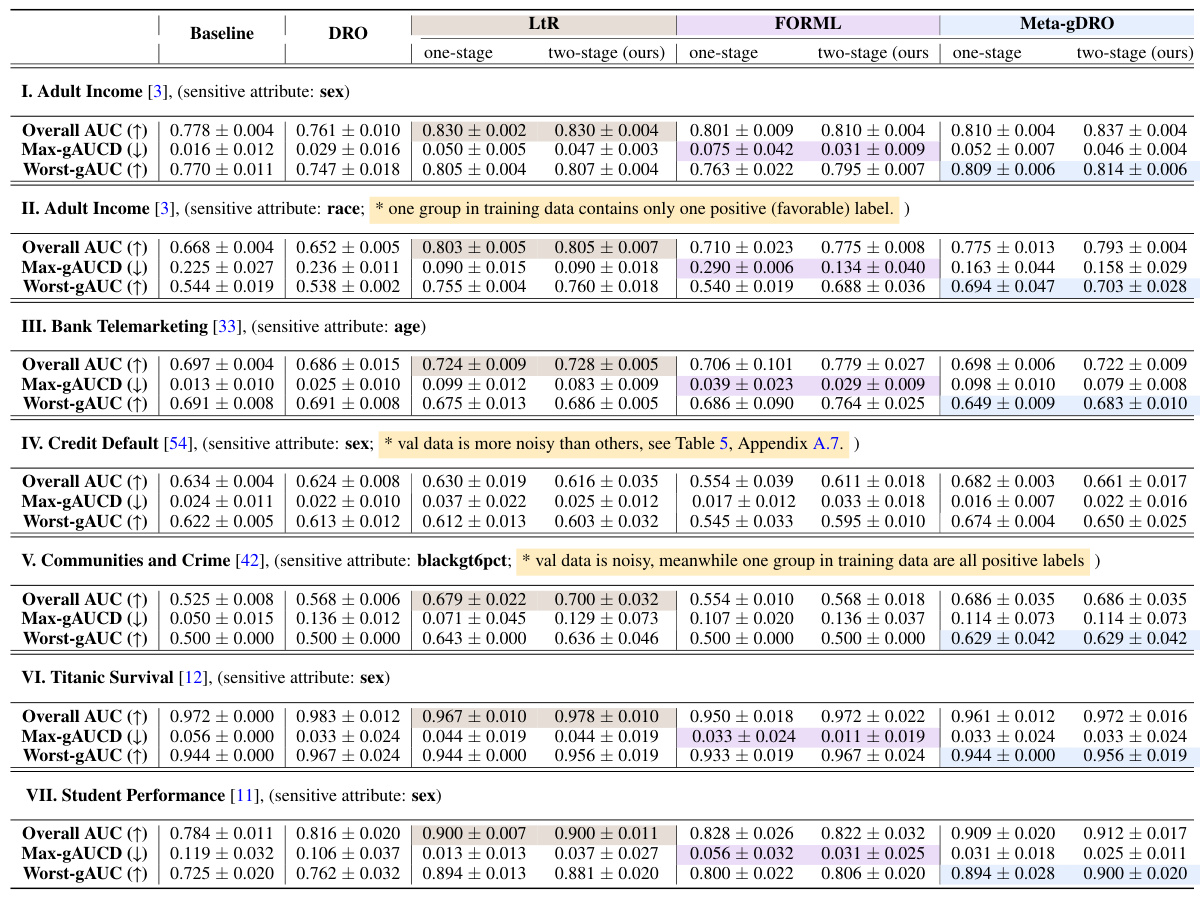
This table compares the performance of the proposed two-stage Nash-Meta-Learning method with three conventional one-stage meta-learning methods (LtR, FORML, Meta-gDRO) and a baseline method (DRO) across six standard fairness datasets. For each dataset and method, the overall AUC (Area Under the Curve), maximum group AUCD (AUC Disparity), and worst-group AUC are reported. The table highlights the improvements achieved by the proposed method in terms of overall performance and fairness.

This table shows the performance of three different one-stage fairness-aware meta-learning methods (LtR, FORML, and Meta-gDRO) in terms of hypergradient alignment. It demonstrates that the proportion of batches where the hypergradients are aligned with the fairness objectives varies significantly between the different methods. The table also shows how frequently the set of feasible update directions (A) was non-empty during the first 15 training epochs.
Full paper#



















