TL;DR#
Current large language models (LLMs) struggle with long context, often relying on techniques like adjusting RoPE’s base parameter to extend context length. However, this approach can lead to superficial improvements. This paper introduces a new theoretical property of RoPE, called “long-term decay,” showing that the model’s ability to focus on similar tokens decreases with distance. This decay is tied to RoPE’s base, establishing a theoretical lower bound that limits achievable context length.
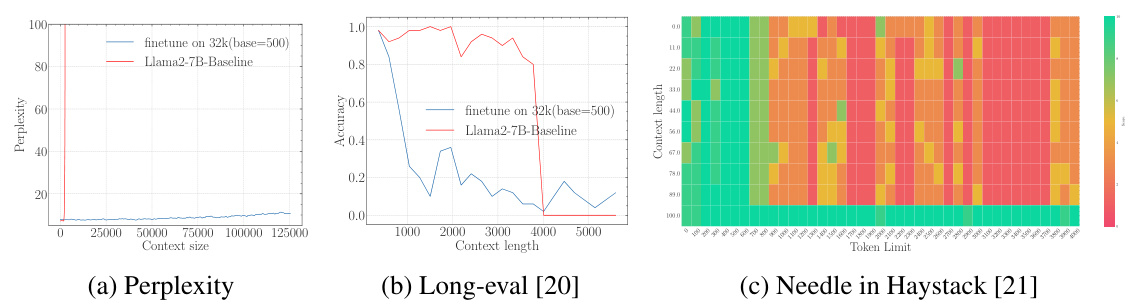
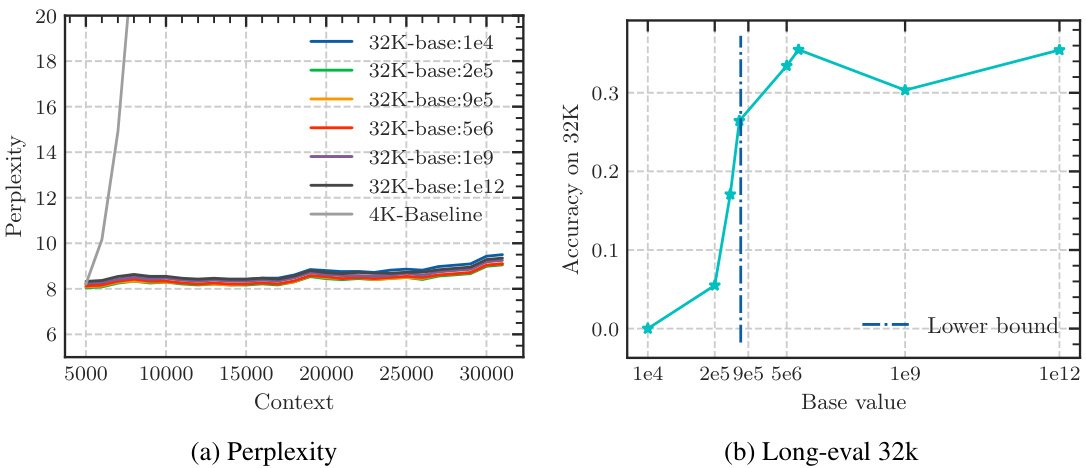
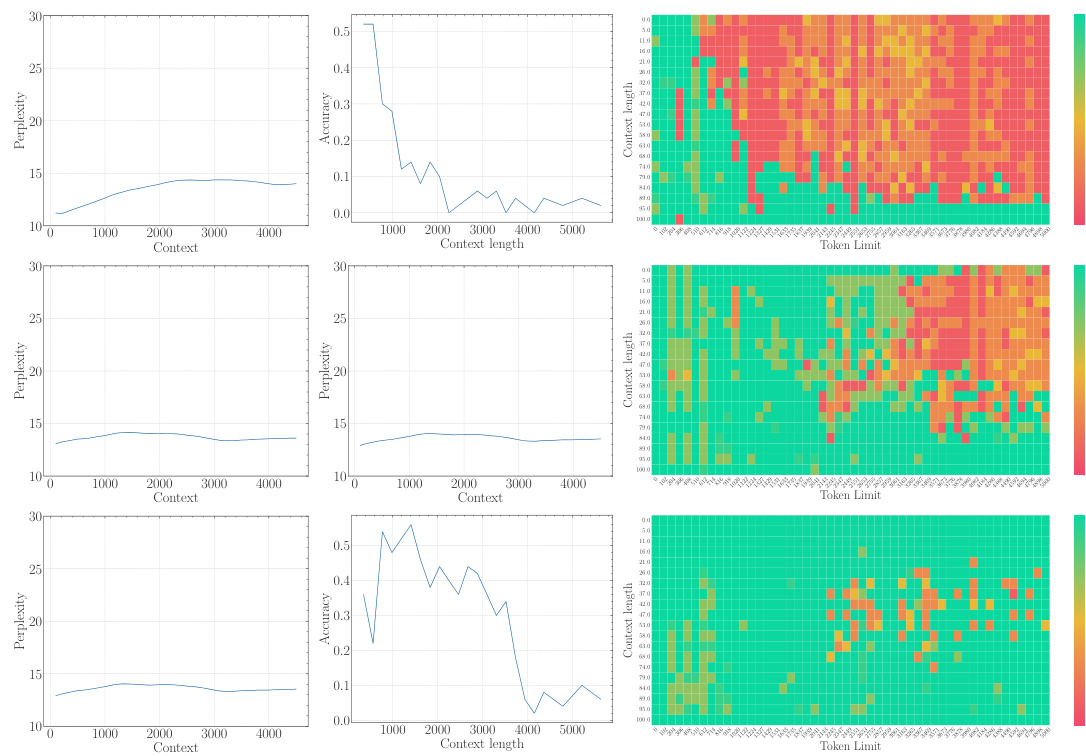
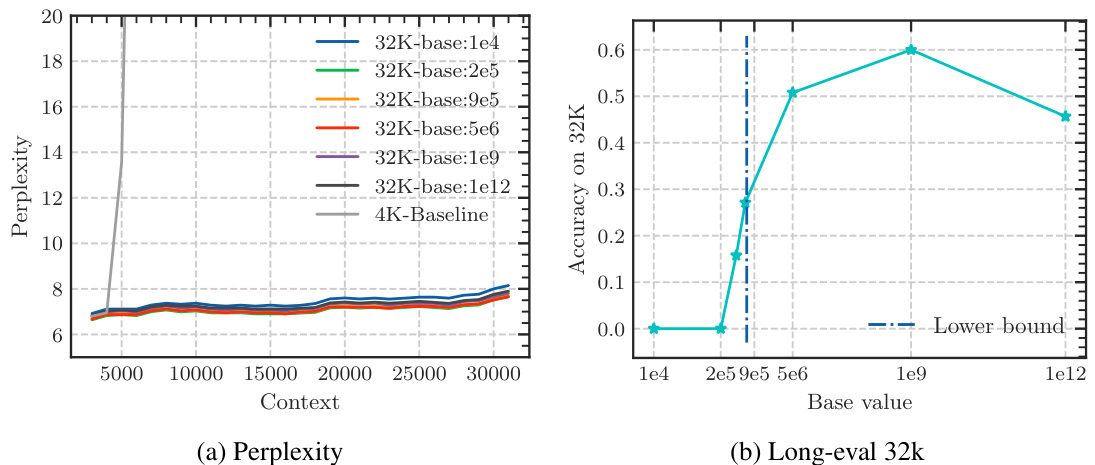
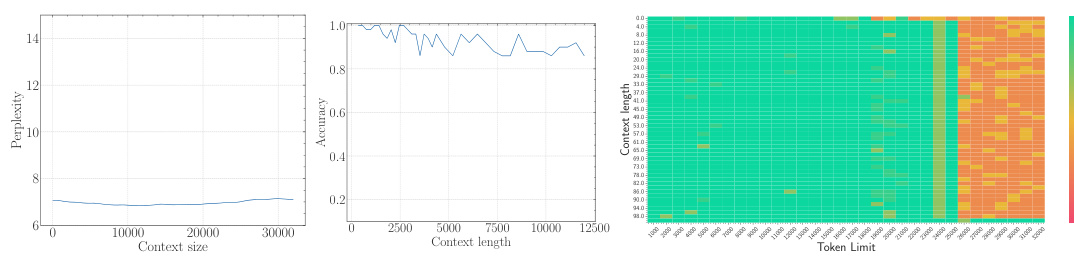
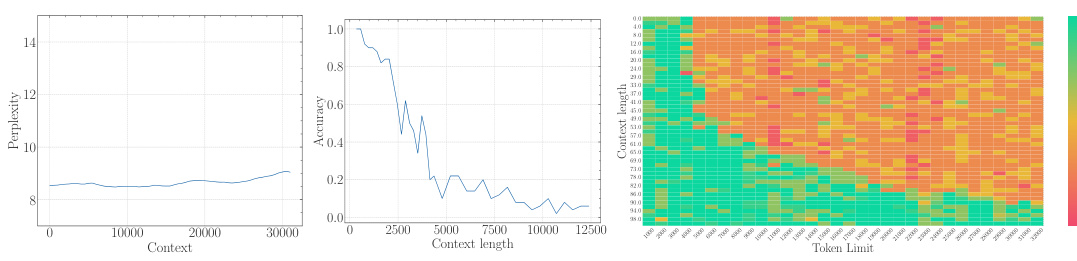
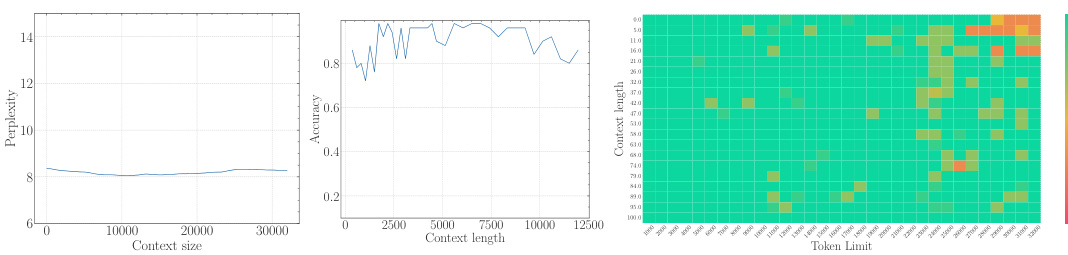
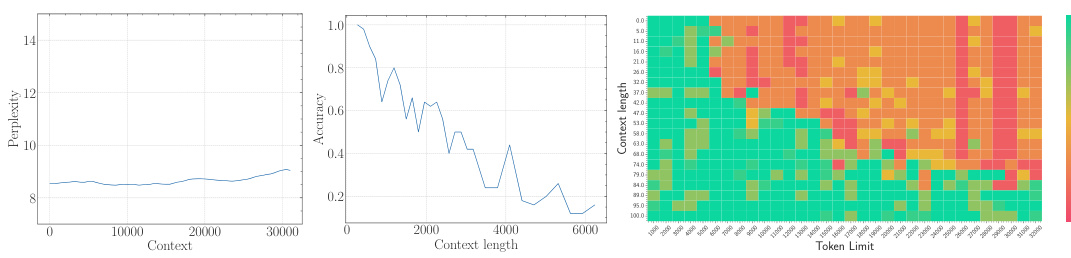
The study presents empirical evidence confirming this lower bound across multiple LLMs. They demonstrate that simply increasing context length without adjusting the RoPE base sufficiently will not yield true long-context capability. Furthermore, using an insufficiently large base leads to superficial long-context capability: low perplexity is maintained, but the model fails to effectively retrieve information from long contexts.
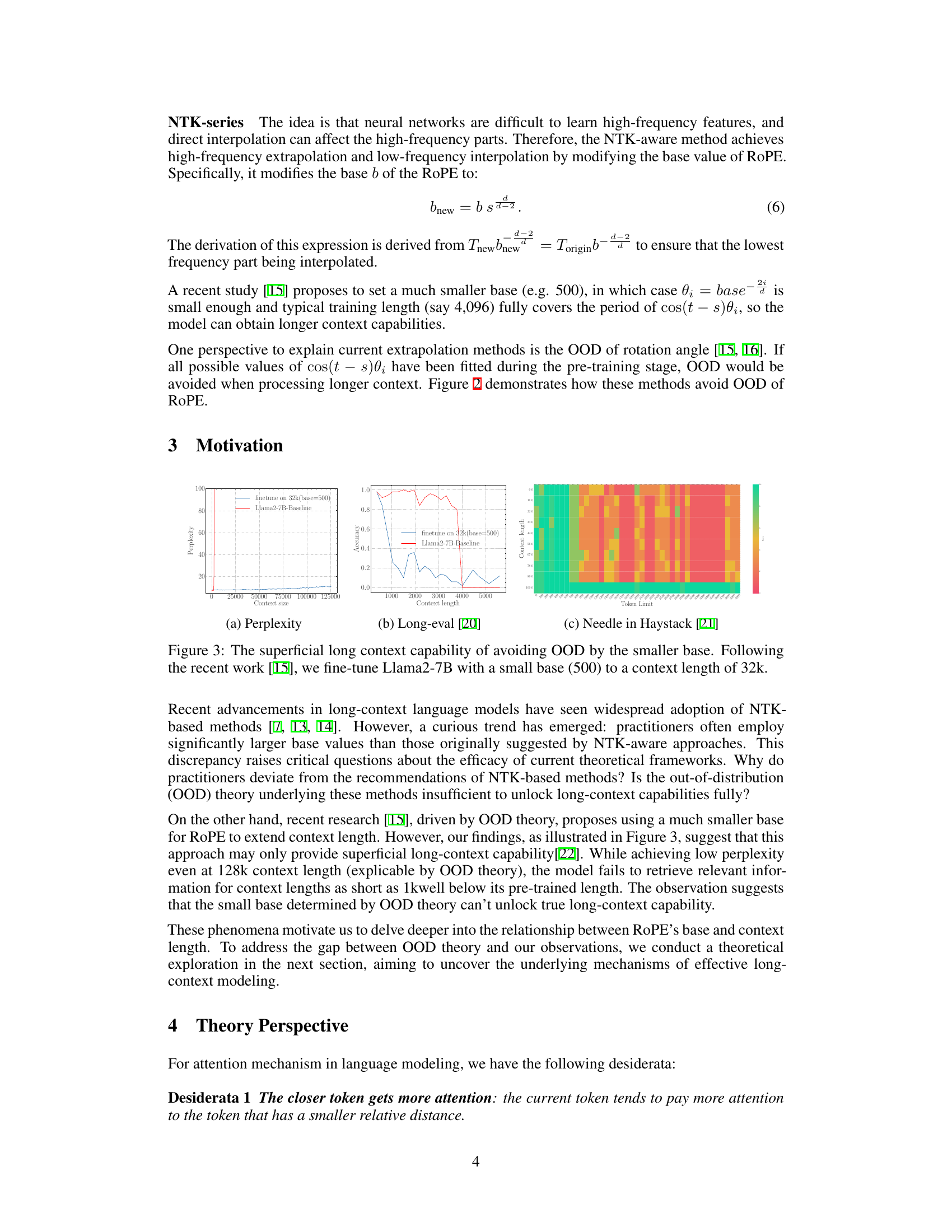
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on large language models (LLMs) and long-context understanding. It challenges existing assumptions about extending LLMs’ context length, offering a novel theoretical perspective and empirical evidence. This work opens new avenues for improving the long-context capabilities of LLMs by addressing the limitations of current extrapolation methods, ultimately impacting various downstream applications.
Visual Insights#
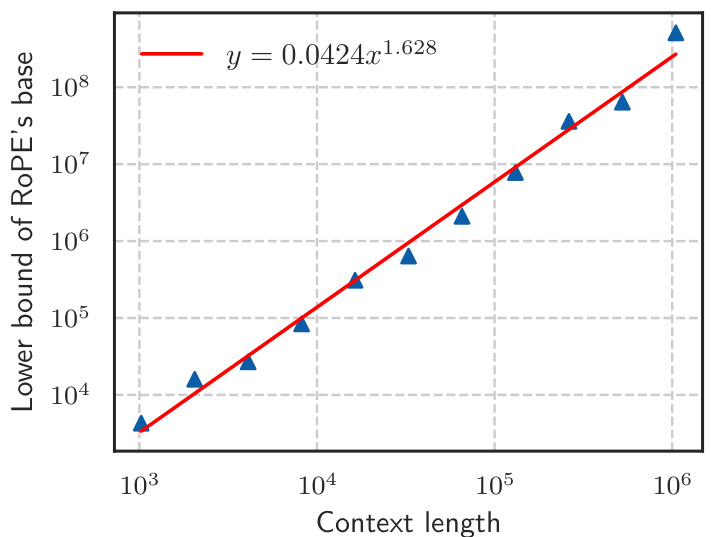
🔼 The figure shows the relationship between the context length and the lower bound of the RoPE’s base value. The x-axis represents the context length, and the y-axis represents the lower bound of the RoPE’s base value. The data points show an exponential relationship between context length and base value, fitting the power-law curve y = 0.0424x^1.628. This indicates that to achieve a longer context length capability, a larger RoPE base value is needed. The figure visually supports the paper’s claim that the base of RoPE bounds the context length.
read the caption
Figure 1: Context length and its corresponding lower bound of RoPE's base value.

🔼 This table shows the relationship between the context length and the lower bound of the RoPE base value. For a given context length (e.g., 1k, 2k, 4k, etc.), the table provides the minimum base value required to achieve that context length capability. The values are expressed in scientific notation (e.g., 4.3e3 means 4.3 x 10^3 or 4300). This table is a key finding of the paper, demonstrating a fundamental constraint of RoPE in extending the context window of large language models.
read the caption
Table 1: Context length and its corresponding lower bound of RoPE's base.
In-depth insights#
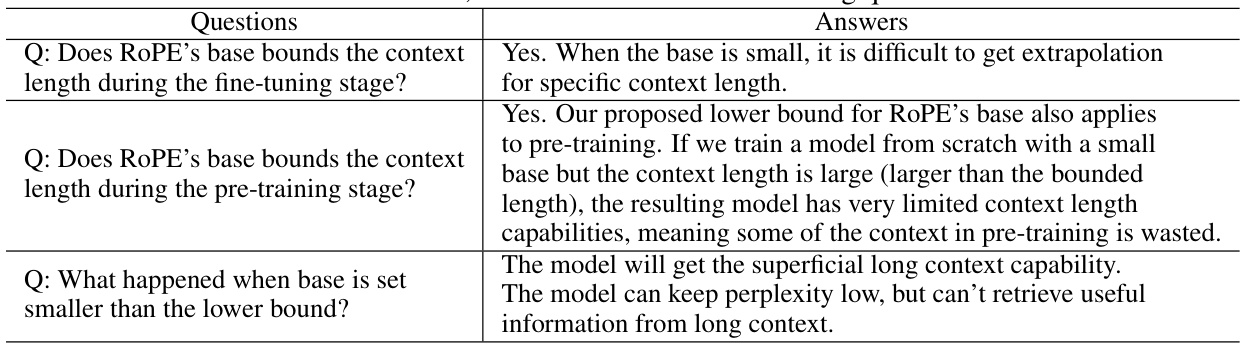
RoPE Base Bounds#
The concept of “RoPE Base Bounds” centers on the crucial role of the base hyperparameter in Rotary Position Embedding (RoPE) within large language models (LLMs). The authors demonstrate that this base parameter is not merely a scaling factor for context length but rather directly bounds the model’s ability to effectively process long sequences. A lower bound exists, below which the LLM demonstrates superficial long-context capabilities; achieving low perplexity but failing to accurately retrieve information from longer sequences. This finding challenges existing approaches that solely focus on mitigating out-of-distribution (OOD) problems via base manipulation, highlighting the importance of considering an absolute minimum base value for achieving true long-context understanding. This work provides a theoretical underpinning for this bound, backed by empirical evidence showcasing its impact across various LLMs and pre-training stages. The theoretical framework introduced, involving concepts such as long-term decay in RoPE’s attention mechanism, offers valuable insight into the intricate relationship between attention scores and relative token similarity in long sequences. This research suggests that future LLM development focusing on long context needs to account for this inherent base bound to ensure genuine, rather than superficial, long-context processing.
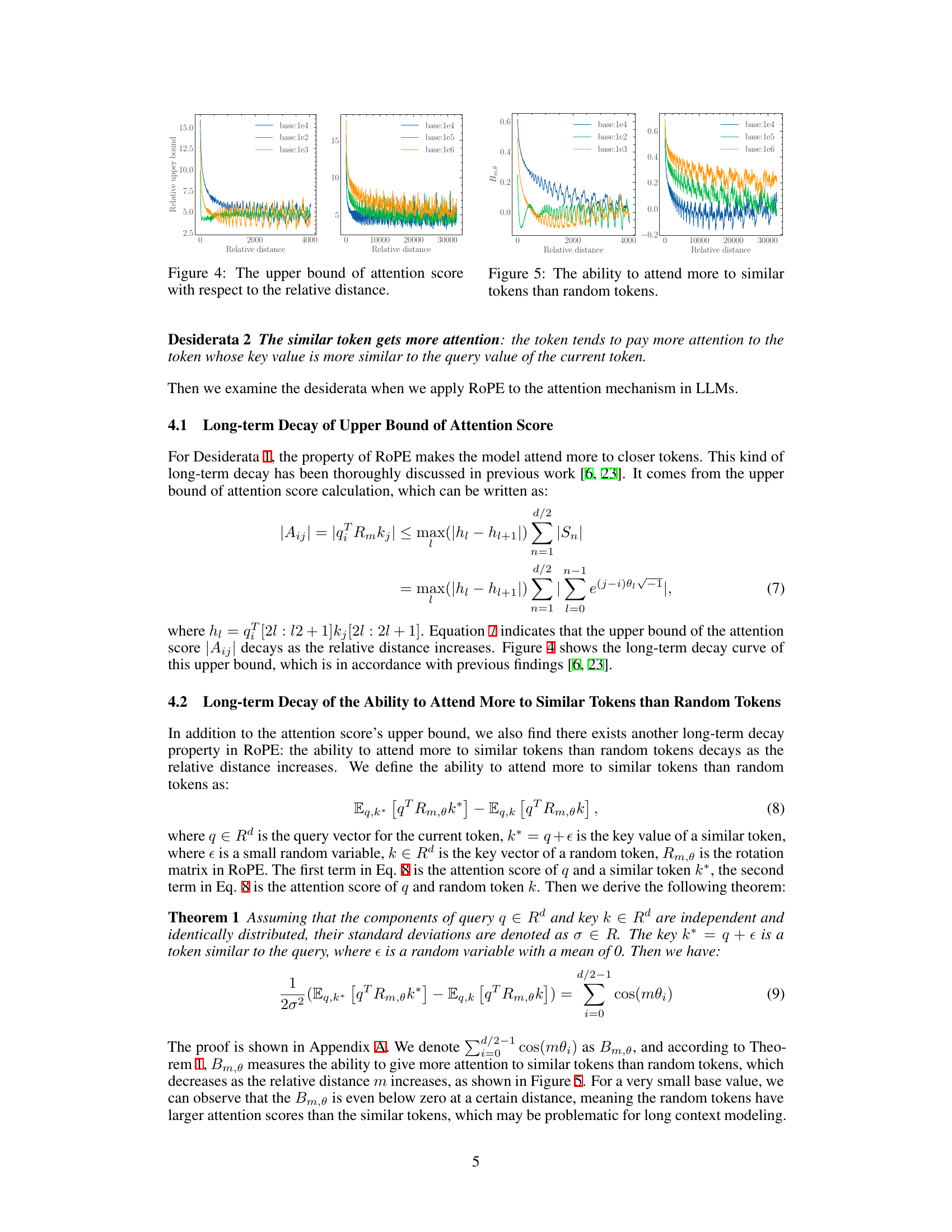
Long-Term Decay#
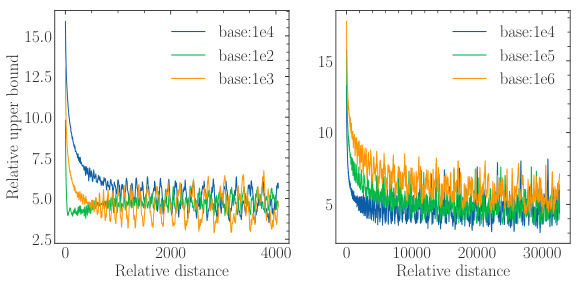
The concept of “Long-Term Decay” in the context of the research paper, likely refers to the phenomenon where the model’s ability to attend to relevant information diminishes as the relative distance from the current token increases. This decay isn’t uniform but is shaped by the RoPE (Rotary Position Embedding) mechanism and its base parameter. A smaller base value exacerbates this decay, potentially leading to superficial long-context capabilities where the model preserves low perplexity but struggles to retrieve actual information from longer distances. The research highlights the crucial interplay between RoPE’s base, long-term decay, and the model’s actual long-context understanding. This decay is not simply a matter of out-of-distribution (OOD) effects, as the paper demonstrates, but a fundamental property of the RoPE mechanism that limits the model’s ability to effectively process long sequences. The analysis suggests the existence of an absolute lower bound on the RoPE base value for a given context length; falling below this bound severely limits the model’s ability to attend to relevant information, confirming the importance of carefully selecting the RoPE base value during both pre-training and fine-tuning.
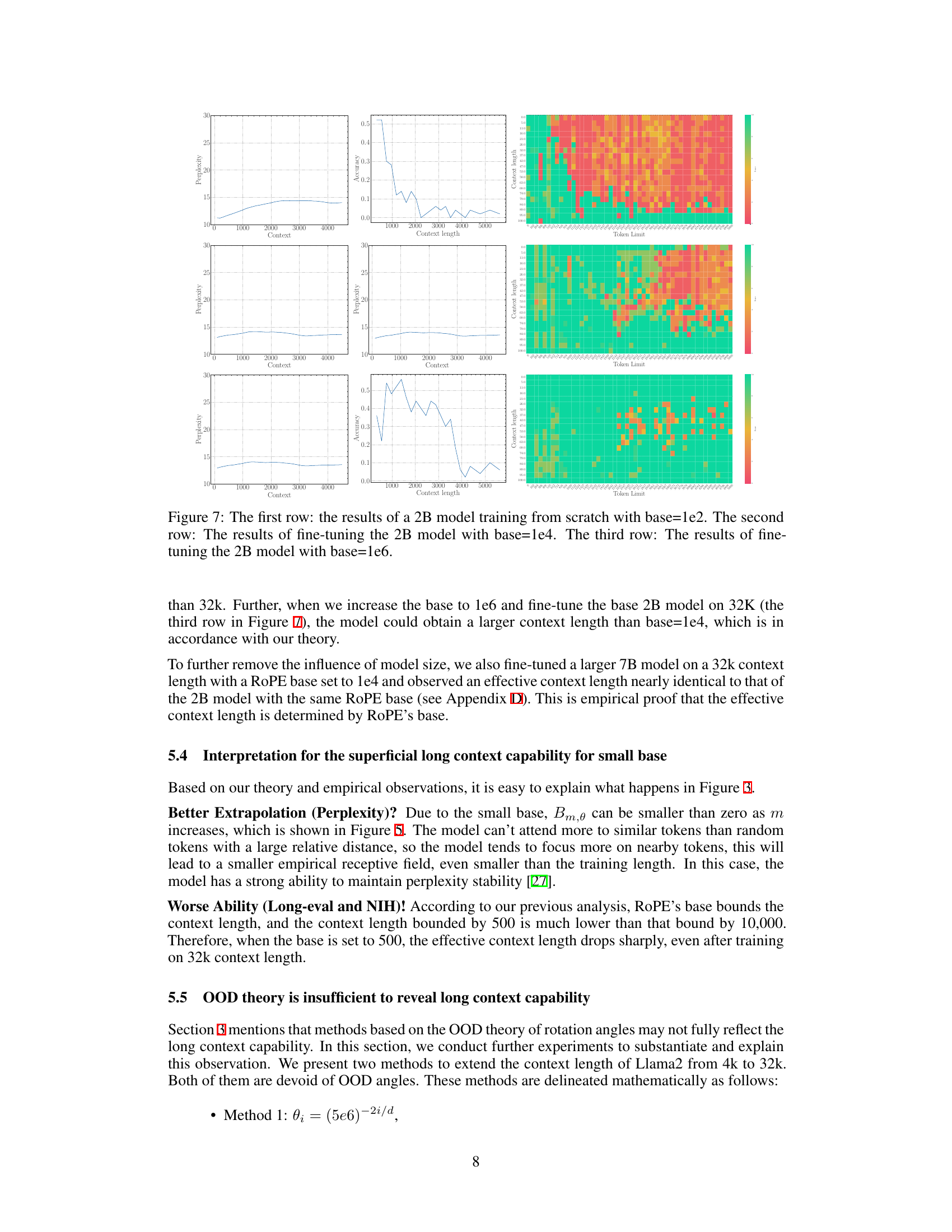
Empirical Findings#
The empirical findings section of a research paper would present concrete evidence supporting or refuting the study’s hypotheses. For a paper on the base of ROPE (Rotary Position Embedding) and its relationship to context length in LLMs, this section would likely involve experiments on multiple LLMs with varying RoPE base values and context lengths. Key results would demonstrate the relationship between the RoPE base and the model’s ability to process long context, showing whether a lower bound for the RoPE base exists to achieve a certain context length. The findings would likely show a trade-off: smaller bases might improve perplexity for long sequences, but they could lead to a loss of long context information retrieval capability. Perplexity scores and long-context evaluation metrics (e.g., LongEval accuracy, Needle in a Haystack performance) would be crucial data points to present. Results would also address whether this relationship holds true during both the pre-training and fine-tuning stages, potentially showing that using a RoPE base value below the theoretical lower bound leads to a superficial long context ability, where low perplexity is observed but actual information retrieval suffers. Overall, a robust empirical findings section would provide clear and compelling evidence that supports or challenges the paper’s core arguments, using statistically sound methods and visualizations to present the data in an easily understandable manner.
Superficial Capability#
The concept of “Superficial Capability” highlights a critical finding: LLMs can exhibit impressive performance on surface-level metrics (like low perplexity) when extended to longer contexts, even with suboptimal RoPE base values. However, this performance is deceptive, masking a fundamental inability to accurately process and retrieve information from the extended context. The model may appear to understand, yet its comprehension is shallow and unreliable, failing to grasp the true meaning and relationships within the longer sequence. This superficial competence is attributed to the limitations of the OOD theory, which does not fully capture the nuanced dynamics of attention and long-range dependencies in LLMs. A low RoPE base, while mitigating out-of-distribution issues, compromises the model’s ability to distinguish between genuinely similar tokens and random tokens over long distances, resulting in a misleading appearance of improved long-context capabilities. Therefore, focusing solely on surface metrics can be misleading, highlighting the importance of deeper evaluations to assess genuine long-context understanding.
Future Research#
Future research directions stemming from this paper could explore the precise mathematical formulation of the RoPE base lower bound, moving beyond the empirical estimations provided. Investigating the interaction between RoPE and other components of LLMs, such as the attention mechanism or normalization layers, could reveal further insights into long-context capabilities. A key area is refining the understanding of superficial long-context ability, perhaps by developing metrics that better capture genuine long-range dependency understanding beyond low perplexity. Furthermore, research should focus on extending the theoretical framework to other position embedding methods beyond RoPE, to explore whether similar bounds or properties exist. Finally, a crucial area for future work is developing more robust and efficient training strategies specifically tailored to achieve truly extended context lengths, potentially leveraging insights gained from understanding the RoPE base bounds.
More visual insights#
More on figures
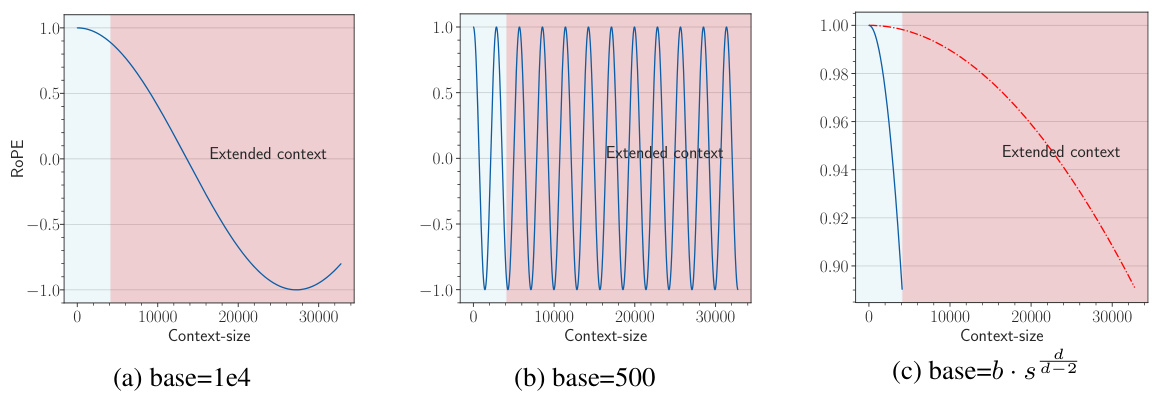
🔼 This figure illustrates the out-of-distribution (OOD) problem in Rotary Position Embedding (RoPE) when extending context length and proposes two solutions. The leftmost panel shows the OOD region when using a standard base value (1e4) for a 4k context model extended to 32k. The middle panel shows that using a much smaller base (500) avoids the OOD problem. The rightmost panel demonstrates another method to prevent OOD by adjusting the base according to the Neural Tangent Kernel (NTK) theory.
read the caption
Figure 2: An illustration of OOD in RoPE when we extend context length from 4k to 32k, and two solutions to avoid the OOD. We show the last dimension as it is the lowest frequency part of ROPE, which suffers OOD mostly in extrapolation. (a) For a 4k context-length model with base value as 1e4, when we extend the context length to 32k without changing the base value, the context length from 4k to 32k is OOD for RoPE (red area in the figure). (b) OOD can be avoided with a small base value like 500 [15], since the full period has been fitted during fine-tuning stage. (c) We set base as b. s2 from NTK [11].The blue line denotes the pre-training stage (base=1e4) and the red dashed line denotes the fine-tuning stage (base=b · sa−2), we can observe that the RoPE's rotation angle of extended positions is in-distribution.
🔼 This figure shows the relationship between the context length and the lower bound of the RoPE base value. The x-axis represents the context length (log scale), and the y-axis represents the lower bound of the RoPE base value (log scale). The data points are fitted with a power-law curve, indicating that as the context length increases, the required minimum value of RoPE’s base parameter also increases. This demonstrates that there’s a lower bound for the base value needed to achieve a certain context length capability.
read the caption
Figure 1: Context length and its corresponding lower bound of RoPE's base value.
🔼 This figure shows the relationship between the context length and the lower bound of the RoPE’s base value. The x-axis represents the context length (log scale), and the y-axis represents the lower bound of the RoPE base value (log scale). A fitted curve is also displayed to show the trend of the relationship. The figure empirically demonstrates the existence of a lower bound on the RoPE base value required to achieve a given context length in LLMs.
read the caption
Figure 1: Context length and its corresponding lower bound of RoPE's base value.

🔼 This figure shows the relationship between the context length and the lower bound of the RoPE base value. The x-axis represents the context length (in tokens), and the y-axis represents the lower bound of the RoPE base. The plot shows an exponential relationship: as the context length increases, so does the minimum required RoPE base value. This is crucial because the paper argues that the RoPE base fundamentally limits the effective context length a language model can handle. A base value below the curve for a given context length will result in the model failing to utilize the full context effectively, despite potentially maintaining low perplexity.
read the caption
Figure 1: Context length and its corresponding lower bound of RoPE's base value.
🔼 This figure shows the relationship between the context length and the lower bound of the RoPE base value. The x-axis represents the context length, and the y-axis represents the lower bound of the RoPE base. The data points are fitted to a power-law curve, demonstrating a strong correlation between context length and the minimum RoPE base required to achieve that context length capability. This empirical observation supports the paper’s claim that the RoPE base value fundamentally bounds the achievable context length in large language models.
read the caption
Figure 1: Context length and its corresponding lower bound of RoPE's base value.
🔼 This figure shows the relationship between the context length and the lower bound of the RoPE base value. The x-axis represents the context length, and the y-axis represents the lower bound of the RoPE’s base value. The plotted points show an exponential relationship, implying that longer context lengths require significantly larger base values in the RoPE position embeddings. The equation of the fitted curve is also provided, showing the empirical relationship between these two variables.
read the caption
Figure 1: Context length and its corresponding lower bound of RoPE's base value.

🔼 This figure shows the relationship between the context length and the lower bound of the RoPE base value. The x-axis represents the context length (log scale), and the y-axis represents the lower bound of the RoPE base value (log scale). The data points suggest a power-law relationship between context length and the minimum RoPE base needed to achieve that length. The line is a power-law fit to the data, showing an approximately exponential increase in the minimum RoPE base required as the desired context length increases.
read the caption
Figure 1: Context length and its corresponding lower bound of RoPE's base value.
🔼 This figure shows the relationship between the context length and the lower bound of the RoPE base value. The x-axis represents the context length, and the y-axis represents the lower bound of the RoPE base value. The data points are fitted to a power law function, which shows that the lower bound of the RoPE base value increases with the context length. This suggests that there is an inherent limit to the context length that can be achieved by simply increasing the base value of RoPE. The figure provides empirical evidence that supports the theoretical findings of the paper.
read the caption
Figure 1: Context length and its corresponding lower bound of RoPE's base value.

🔼 This figure shows the relationship between the context length and the lower bound of the RoPE base value. The x-axis represents the context length, and the y-axis represents the lower bound of the RoPE base. The plot shows an exponential relationship; as the context length increases, the required minimum RoPE base value increases exponentially. This empirically demonstrates that RoPE’s base value places a lower bound on the model’s context length capacity.
read the caption
Figure 1: Context length and its corresponding lower bound of RoPE's base value.
🔼 This figure shows the relationship between the context length and the lower bound of the RoPE base value. The x-axis represents the context length, and the y-axis represents the lower bound of the RoPE base value. The data points are fitted with a power law function, indicating a strong correlation between context length and RoPE’s base value. This suggests that there is a minimum base value required to achieve a certain context length capability.
read the caption
Figure 1: Context length and its corresponding lower bound of RoPE's base value.
🔼 This figure shows the relationship between the context length and the lower bound of the RoPE base value. The x-axis represents the context length, and the y-axis represents the lower bound of the RoPE base value. The plot shows an exponential relationship, indicating that as the context length increases, the required RoPE base value also increases exponentially to maintain the model’s ability to effectively process long contexts.
read the caption
Figure 1: Context length and its corresponding lower bound of RoPE's base value.
🔼 This figure shows the relationship between the context length and the lower bound of the RoPE base value. The x-axis represents the context length, and the y-axis represents the lower bound of the RoPE base. The plot shows an exponential relationship, indicating that as the desired context length increases, the minimum required base value for RoPE also increases exponentially. This is a key finding of the paper, demonstrating a theoretical lower bound on the RoPE base for achieving a certain context length.
read the caption
Figure 1: Context length and its corresponding lower bound of RoPE's base value.
🔼 This figure shows the relationship between the context length and the lower bound of the RoPE base value. The x-axis represents the context length, and the y-axis represents the lower bound of the RoPE base value. The figure shows that as the context length increases, the lower bound of the RoPE base value also increases. This suggests that there is a minimum RoPE base value required to achieve a certain context length capability. The figure also shows a power law relationship between context length and ROPE base value, with the equation of the fitted curve being y = 0.0424x^1.628.
read the caption
Figure 1: Context length and its corresponding lower bound of RoPE's base value.
More on tables
🔼 This table shows the relationship between the context length and the lower bound of the RoPE base value. For a given context length, there is a minimum base value required for the model to effectively utilize that context length. The table lists these lower bound values for various context lengths, ranging from 1,000 to 1 million tokens.
read the caption
Table 1: Context length and its corresponding lower bound of RoPE's base.

🔼 This table compares two methods, Method 1 and Method 2, designed to avoid out-of-distribution (OOD) issues in the context of extending the context length of Language Models. Despite both avoiding OOD, their performance on the Long-eval task differs significantly, highlighting that avoiding OOD alone doesn’t guarantee good long-context capabilities. Method 2, while technically avoiding OOD, shows substantially worse performance in the Long-eval metric (0.00 vs 0.27 at 30k context length). The number of m values (relative distances) where Bm,θ (a function representing the ability to attend to similar tokens over random ones) is less than or equal to 0 is much higher for Method 2, indicating a failure to maintain the desired attention properties at longer distances.
read the caption
Table 3: The comparison of 'Method 1' and 'Method 2'. These methods are designed carefully. They both are no OOD, but they are very different under our theory.

🔼 This table lists the hyperparameters used in the experiments described in the paper. It shows the training length, training tokens, batch size, base learning rate, learning rate decay method, and weight decay for three different models: Llama2-7B-Base, Baichuan2-7B-Base, and a 2B model trained from scratch by the authors. The differences in hyperparameters reflect the different training approaches used for each model.
read the caption
Table 4: Training hyper-parameters in our experiments

🔼 This table presents the evaluation results of the RULER benchmark. Llama2-7B is fine-tuned to a context length of 32k using various RoPE base values (the lowest bound is 6e5). The results are broken down by subtasks (NS-1 through NS-3, NM-1 through NM-3, NIAH_Multivalue, NIAH_Multiquery, VT, CWE, FWE, QA1, QA2), showing the performance with different RoPE bases for each subtask and context length.
read the caption
Table 5: Evaluation results on RULER. We finetune Llama2-7b to 32k context length (the low bound base is 6e5) using different RoPE's bases. NS is short for NIAH-single and NM is short for NIAH-Multikey.
Full paper#