TL;DR#
Offline reinforcement learning (RL) aims to learn effective policies from existing data without additional online interactions. However, existing model-free methods often struggle due to extrapolation errors caused by out-of-distribution actions and the difficulty of handling multi-modal policy distributions. Distribution Correction Estimation (DICE) methods offer an implicit regularization technique but are limited by unimodal Gaussian policy extraction.
This paper introduces Diffusion-DICE, a novel offline RL approach that tackles these limitations. It views DICE methods as a transformation from behavior to optimal policy distributions and leverages diffusion models to perform this transformation directly. By carefully selecting actions using a value function, it minimizes error exploitation and outperforms existing diffusion-based and DICE-based methods in benchmark evaluations. The in-sample learning objective further enhances its robustness and efficiency.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel approach to offline reinforcement learning (RL) that significantly improves performance by addressing the limitations of existing methods. It introduces a new paradigm of guide-then-select and uses diffusion models for efficient policy transformation, opening new avenues for research in offline RL. Its strong empirical results on benchmark datasets highlight its practical significance and potential impact on various applications.
Visual Insights#
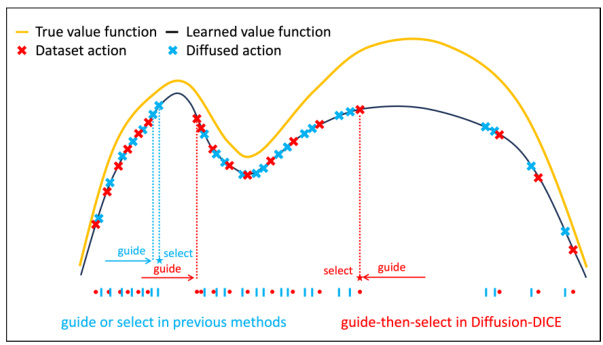
🔼 This figure illustrates the difference between the guide-then-select paradigm used in Diffusion-DICE and the guide-only or select-only approaches used in previous diffusion-based offline RL methods. The guide-then-select approach uses in-sample actions for training, minimizing error exploitation in the value function. In contrast, guide-only methods use predictions of actions’ values to guide toward high-return actions, and select-only methods sample many actions and choose the best one according to the value function, both introducing potential error.
read the caption
Figure 1: Illustration of the guide-then-select paradigm
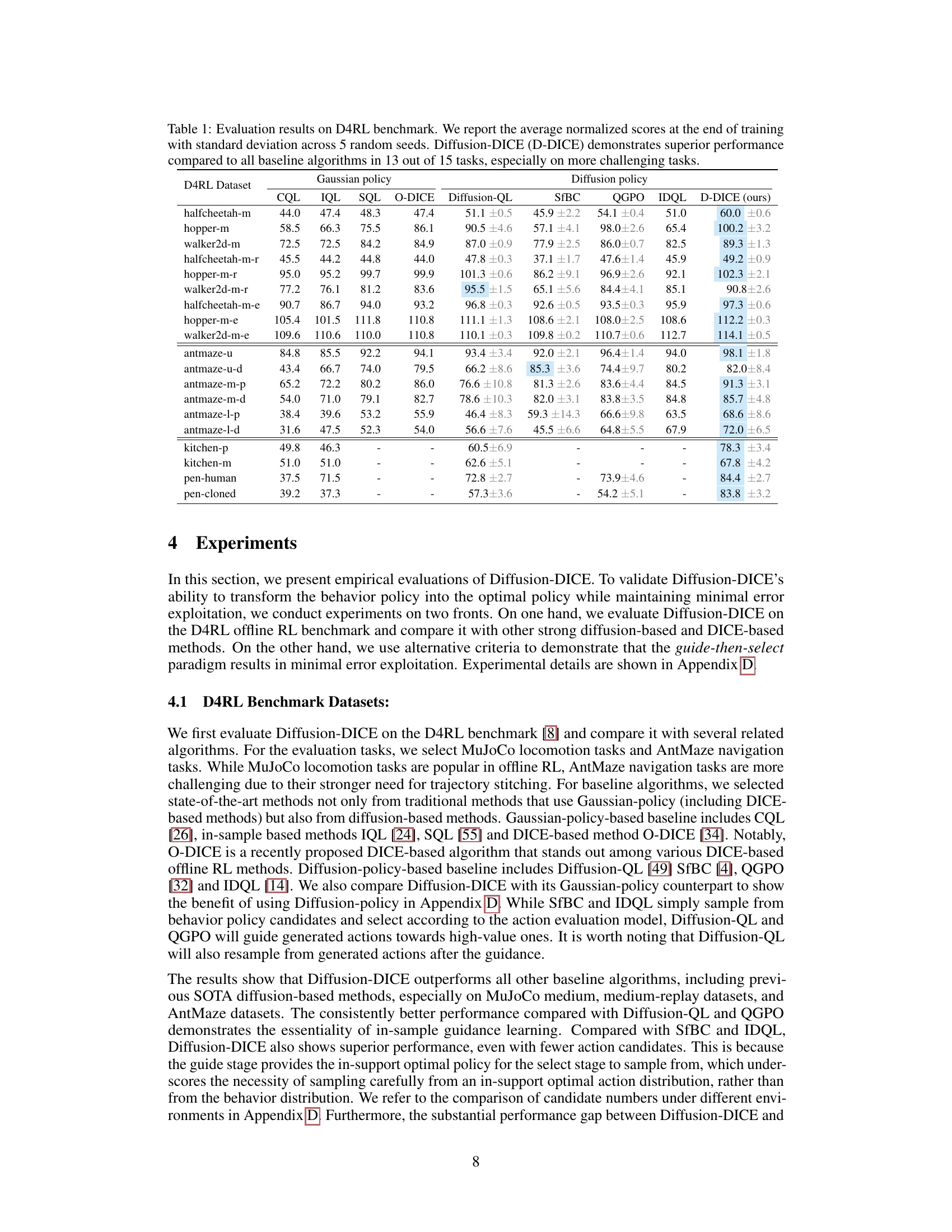
🔼 This table presents the average normalized scores achieved by Diffusion-DICE and several baseline algorithms on 15 different tasks from the D4RL benchmark. The results are averaged across 5 independent runs with standard deviations reported, highlighting the superior performance of Diffusion-DICE on the majority of tasks.
read the caption
Table 1: Evaluation results on D4RL benchmark. We report the average normalized scores at the end of training with standard deviation across 5 random seeds. Diffusion-DICE (D-DICE) demonstrates superior performance compared to all baseline algorithms in 13 out of 15 tasks, especially on more challenging tasks.
In-depth insights#
DICE Transform#
The concept of a “DICE Transform” in offline reinforcement learning (RL) offers a novel perspective on distribution correction methods. It suggests viewing DICE (Distribution Correction Estimation) not merely as an optimization technique but as a direct transformation between the behavior policy distribution and the optimal policy distribution. This reframing allows the use of generative models, such as diffusion models, to directly learn this mapping. The strength of this approach lies in its potential to bypass the limitations of traditional methods that often struggle with multi-modal optimal policy distributions, and to leverage the expressive power of generative models for handling complex probability densities. A key benefit would be the capability of generating in-distribution actions by the transform, thus mitigating the risks of out-of-distribution errors that plague many offline RL techniques. The challenge, however, is the need for careful design to ensure the transform accurately reflects the optimal policy without overfitting to the training data and to handle potential issues of multimodality.
Diffusion Guidance#
Diffusion guidance, in the context of offline reinforcement learning, represents a novel approach to overcome the limitations of traditional methods. It leverages the power of diffusion models to subtly transform the behavior policy distribution into the target optimal policy distribution. This transformation is not a direct mapping but rather a carefully guided process, using the optimal distribution ratio (often learned via DICE) to steer the diffusion process towards high-value, in-distribution actions. The key advantage lies in the in-sample nature of this guidance: it relies solely on data from the observed behavior, minimizing the risk of extrapolation errors from out-of-distribution actions. This approach contrasts with other methods, where direct value estimation on potentially out-of-distribution actions from a diffusion model can lead to significant error. The guide-then-select paradigm further refines the process, generating multiple candidate actions and selecting the optimal one based on an accurate value function. This two-step process enhances efficiency and robustness, particularly in scenarios with multi-modal optimal policies.
In-sample Learning#
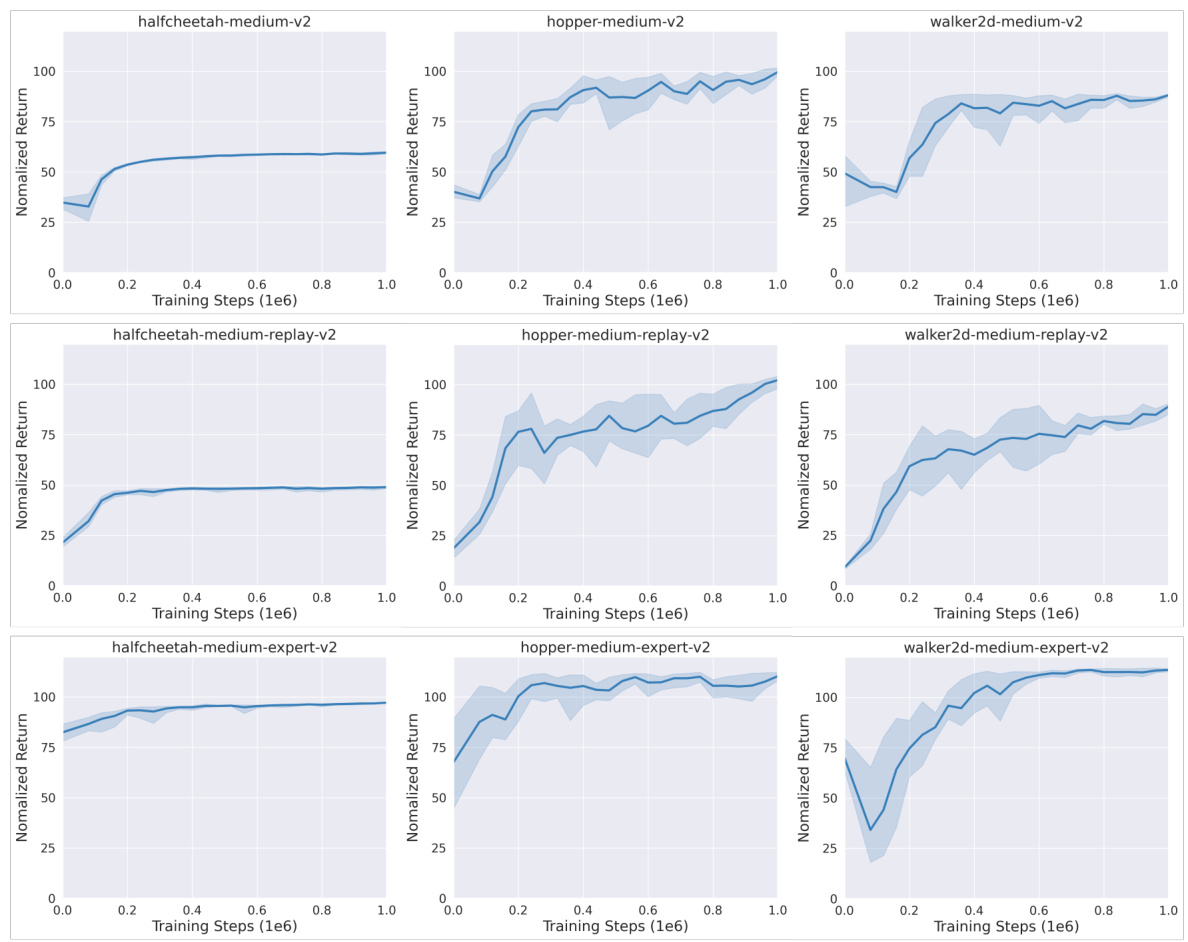
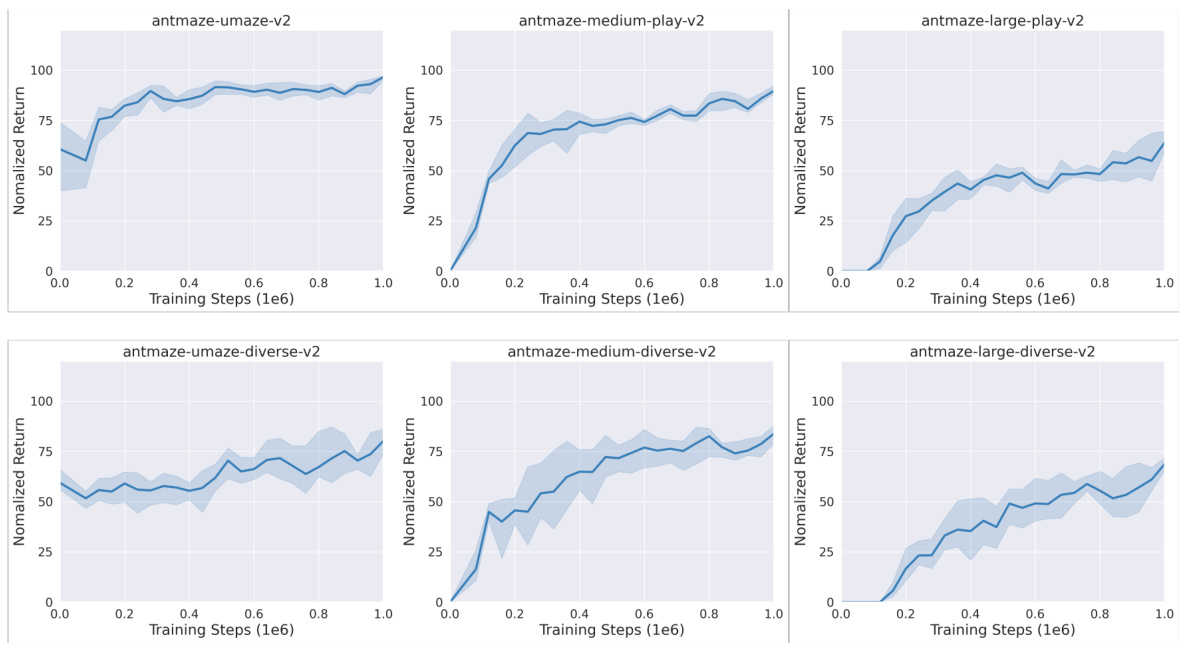
In-sample learning, a crucial aspect of offline reinforcement learning, focuses on training models exclusively using data from the available offline dataset. This approach directly addresses the challenge of avoiding out-of-distribution (OOD) errors, a common pitfall in offline RL. Unlike methods that rely on value function estimates for OOD actions, in-sample learning minimizes error by leveraging only in-distribution actions. This significantly enhances the reliability of the trained policy and avoids the overestimation of value often associated with OOD samples. By restricting training to the data distribution, in-sample learning ensures a more robust and effective policy for the target environment. The key is that the learned policy remains within the bounds of the observed data distribution preventing unpredictable behavior outside of this range. However, the success of this approach is heavily dependent on the quality and representativeness of the initial dataset. A biased or insufficient dataset would likely result in an inadequate policy even with a perfectly implemented in-sample learning strategy.
Guide-then-Select#
The “Guide-then-Select” paradigm offers a novel approach to offline reinforcement learning (RL) by cleverly combining the strengths of generative models and value-based methods. The guidance phase leverages a diffusion model trained on in-sample data to generate candidate actions, which are carefully selected in the selection phase based on their predicted values derived from a critic network. This dual approach helps address several limitations of previous methods. In-sample learning mitigates the issue of extrapolation error, making the method robust and reliable. Multi-modality in optimal policies is addressed by evaluating multiple candidates instead of relying on single actions, potentially improving performance on complex tasks. The framework’s strong performance on benchmark datasets suggests its effectiveness in combining generative modeling and value estimation for offline RL, providing a promising avenue for future research.
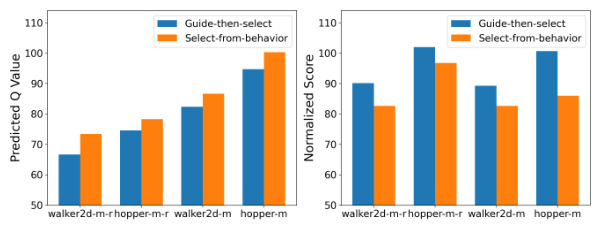
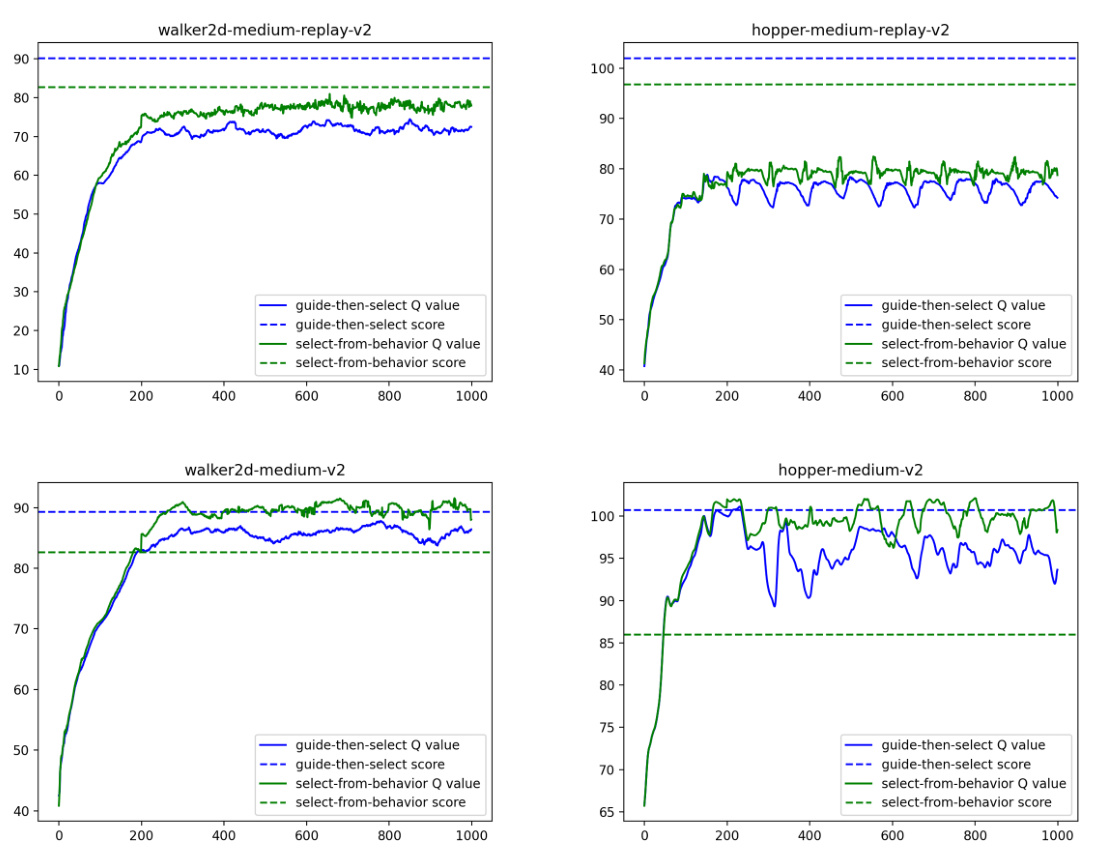
Error Exploitation#
The concept of ’error exploitation’ in offline reinforcement learning (RL) centers on how algorithms might mistakenly leverage errors in their learned models to produce seemingly good, yet ultimately suboptimal, results. Guide-based methods, which use learned value functions to guide the generation of actions, are particularly vulnerable. If the value function contains errors, especially overestimations of out-of-distribution (OOD) actions, the algorithm may be misled towards these inaccurate high-value regions. Select-based methods, which sample many actions and select the best one, can also suffer if the value function is inaccurate. This is because the selection process may pick an OOD action with an erroneously high value. Diffusion-DICE’s strength lies in its ability to mitigate this problem. By focusing on in-sample data and a guide-then-select paradigm, it minimizes reliance on potentially erroneous value estimations for OOD actions, thereby reducing the risk of error exploitation and achieving better performance.
More visual insights#
More on figures

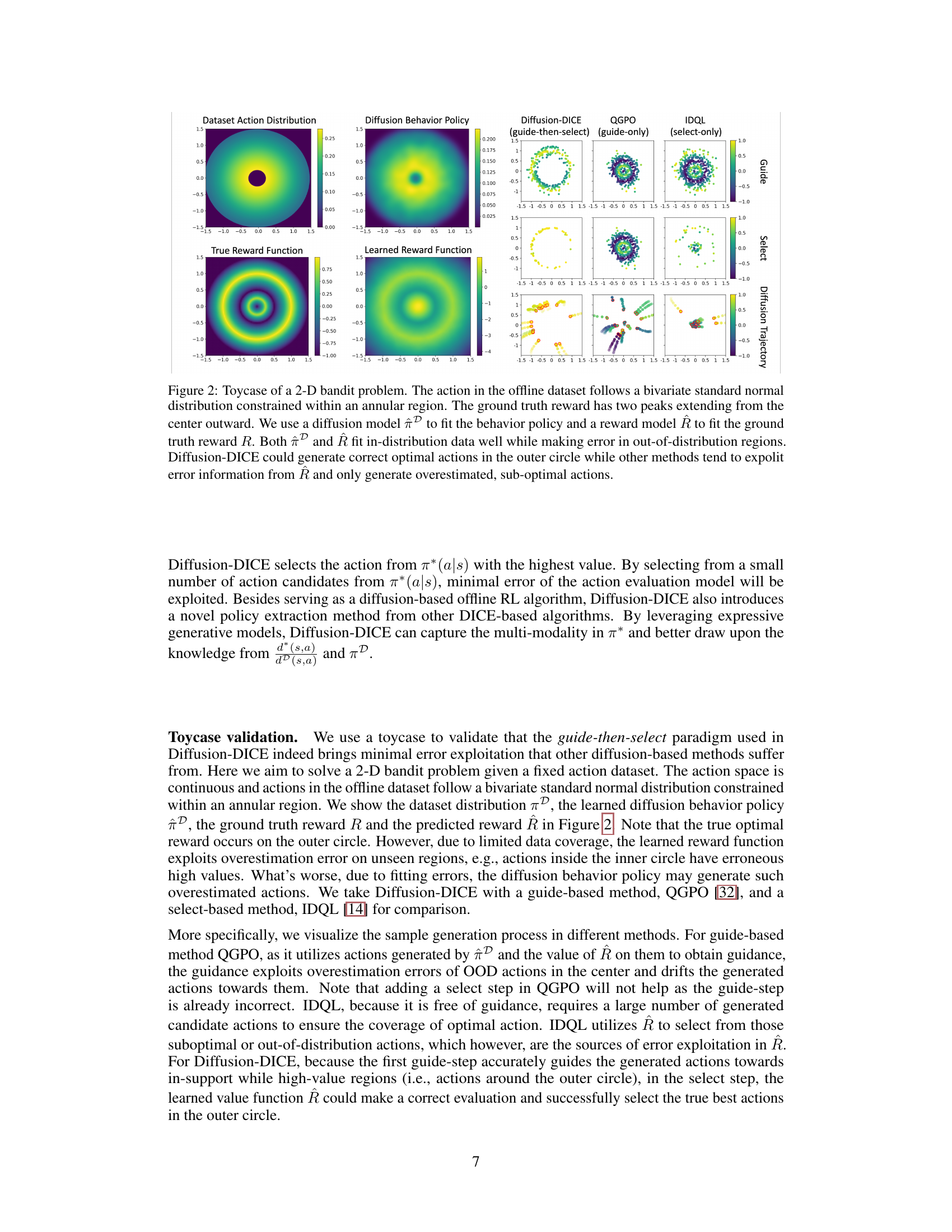
🔼 This figure shows a visualization of a 2D bandit problem used to illustrate the differences between Diffusion-DICE and other offline RL algorithms. The dataset actions are sampled from a bivariate normal distribution, confined within a ring. The true reward function has two peaks in the outer ring. The figure displays the dataset action distribution, a diffusion model fit to the behavior policy, the true and learned reward functions, and the actions sampled by Diffusion-DICE, QGPO, and IDQL. Diffusion-DICE successfully generates actions in the high-reward outer ring, while the others are misled by errors in the learned reward function and generate suboptimal actions in the low-reward inner region. This highlights Diffusion-DICE’s ability to avoid error exploitation.
read the caption
Figure 2: Toycase of a 2-D bandit problem. The action in the offline dataset follows a bivariate standard normal distribution constrained within an annular region. The ground truth reward has two peaks extending from the center outward. We use a diffusion model to fit the behavior policy and a reward model R to fit the ground truth reward R. Both and R fit in-distribution data well while making error in out-of-distribution regions. Diffusion-DICE could generate correct optimal actions in the outer circle while other methods tend to exploit error information from R and only generate overestimated, sub-optimal actions.
🔼 This figure illustrates a 2D bandit problem used to compare Diffusion-DICE against other offline RL methods. The offline dataset consists of actions sampled from a bivariate normal distribution constrained to an annulus. The true reward function has two peaks in the outer regions of the annulus. The figure shows that while the diffusion model and reward model accurately represent the data within the annulus, they misrepresent the data outside the annulus. Diffusion-DICE correctly identifies the optimal actions (in the outer ring), while other methods are misled by errors in the reward model and propose suboptimal actions.
read the caption
Figure 2: Toycase of a 2-D bandit problem. The action in the offline dataset follows a bivariate standard normal distribution constrained within an annular region. The ground truth reward has two peaks extending from the center outward. We use a diffusion model to fit the behavior policy and a reward model R to fit the ground truth reward R. Both and R fit in-distribution data well while making error in out-of-distribution regions. Diffusion-DICE could generate correct optimal actions in the outer circle while other methods tend to exploit error information from R and only generate overestimated, sub-optimal actions.

🔼 This figure shows a 2D bandit problem where the offline dataset’s actions follow a bivariate standard normal distribution within a ring shape. The true reward function has two peaks outside the ring. The figure compares the performance of Diffusion-DICE, QGPO, and IDQL in learning this reward function. It demonstrates that Diffusion-DICE successfully avoids out-of-distribution errors which hinder the other two methods.
read the caption
Figure 2: Toycase of a 2-D bandit problem. The action in the offline dataset follows a bivariate standard normal distribution constrained within an annular region. The ground truth reward has two peaks extending from the center outward. We use a diffusion model to fit the behavior policy and a reward model R to fit the ground truth reward R. Both and R fit in-distribution data well while making error in out-of-distribution regions. Diffusion-DICE could generate correct optimal actions in the outer circle while other methods tend to expolit error information from R and only generate overestimated, sub-optimal actions.
🔼 This figure shows a comparison of different offline RL methods on a 2D bandit problem. The dataset is generated from a bivariate standard normal distribution constrained to an annulus. The reward function has two peaks, one in the inner and one in the outer ring. The figure compares the learned reward function and action distributions of three methods: Diffusion-DICE, QGPO (guide-only), and IDQL (select-only), illustrating how Diffusion-DICE successfully avoids the out-of-distribution action exploitation that plagues the other methods, leading to better performance.
read the caption
Figure 2: Toycase of a 2-D bandit problem. The action in the offline dataset follows a bivariate standard normal distribution constrained within an annular region. The ground truth reward has two peaks extending from the center outward. We use a diffusion model to fit the behavior policy and a reward model R to fit the ground truth reward R. Both and R fit in-distribution data well while making error in out-of-distribution regions. Diffusion-DICE could generate correct optimal actions in the outer circle while other methods tend to exploit error information from R and only generate overestimated, sub-optimal actions.
🔼 This figure illustrates a 2D bandit problem used to compare Diffusion-DICE against other offline RL methods. The offline dataset’s actions follow a bivariate normal distribution within a ring shape. The true reward function has two peaks radiating outwards. The plots show the dataset’s action distribution, the learned diffusion model’s behavior policy, and the true vs. learned reward functions. The comparison highlights how Diffusion-DICE avoids errors from out-of-distribution data to select the optimal actions, unlike other methods.
read the caption
Figure 2: Toycase of a 2-D bandit problem. The action in the offline dataset follows a bivariate standard normal distribution constrained within an annular region. The ground truth reward has two peaks extending from the center outward. We use a diffusion model to fit the behavior policy and a reward model R to fit the ground truth reward R. Both and R fit in-distribution data well while making error in out-of-distribution regions. Diffusion-DICE could generate correct optimal actions in the outer circle while other methods tend to expolit error information from R and only generate overestimated, sub-optimal actions.
🔼 This figure shows a 2D bandit problem where actions are sampled from a bivariate standard normal distribution within a ring. The reward function has two peaks outside the ring. The figure compares the learned reward function and action distributions of several offline RL methods against the ground truth. It highlights how Diffusion-DICE avoids out-of-distribution errors and successfully generates optimal actions, while others fail due to error exploitation.
read the caption
Figure 2: Toycase of a 2-D bandit problem. The action in the offline dataset follows a bivariate standard normal distribution constrained within an annular region. The ground truth reward has two peaks extending from the center outward. We use a diffusion model to fit the behavior policy and a reward model R to fit the ground truth reward R. Both and R fit in-distribution data well while making error in out-of-distribution regions. Diffusion-DICE could generate correct optimal actions in the outer circle while other methods tend to expolit error information from R and only generate overestimated, sub-optimal actions.
More on tables
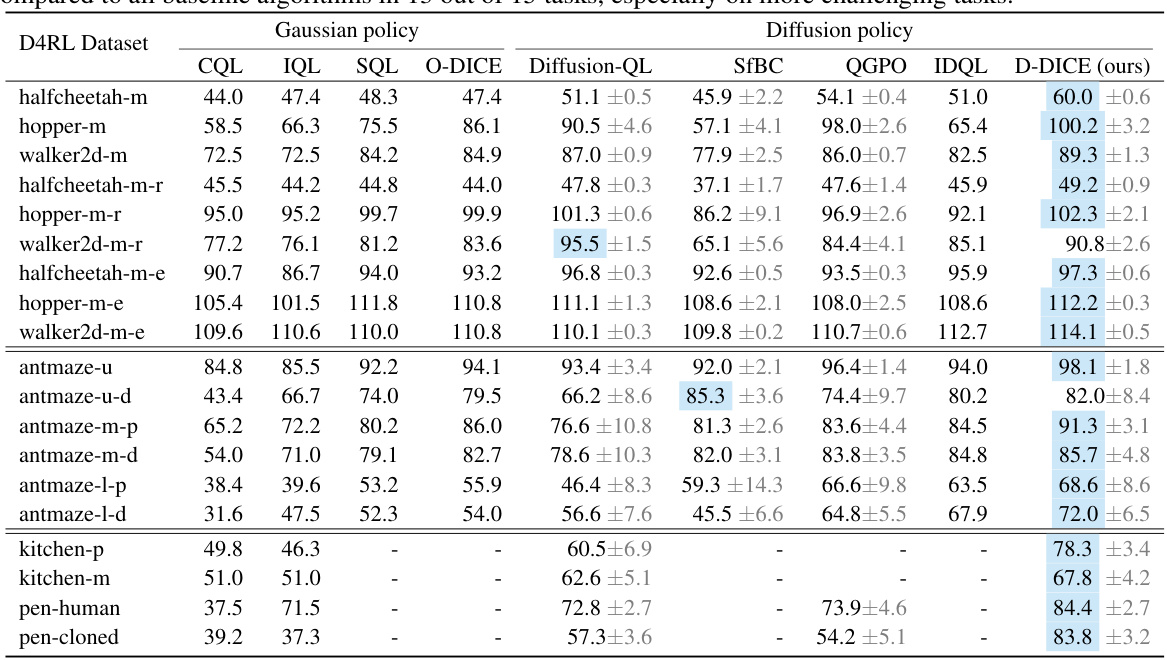
🔼 This table presents the quantitative results of Diffusion-DICE and several baseline algorithms on the D4RL benchmark. The average normalized scores and standard deviations across 5 random seeds are reported for 15 different tasks. The results highlight Diffusion-DICE’s superior performance compared to other methods, particularly on more difficult tasks.
read the caption
Table 1: Evaluation results on D4RL benchmark. We report the average normalized scores at the end of training with standard deviation across 5 random seeds. Diffusion-DICE (D-DICE) demonstrates superior performance compared to all baseline algorithms in 13 out of 15 tasks, especially on more challenging tasks.
🔼 This table presents the quantitative results of Diffusion-DICE and several baseline algorithms on 15 tasks from the D4RL benchmark. The average normalized scores and standard deviations across 5 random seeds are shown for each algorithm and task. Diffusion-DICE outperforms the baselines on most tasks, particularly the more difficult ones.
read the caption
Table 1: Evaluation results on D4RL benchmark. We report the average normalized scores at the end of training with standard deviation across 5 random seeds. Diffusion-DICE (D-DICE) demonstrates superior performance compared to all baseline algorithms in 13 out of 15 tasks, especially on more challenging tasks.
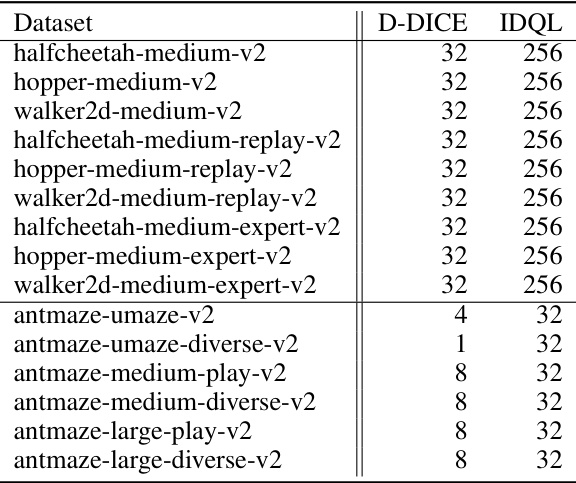
🔼 This table compares the number of action candidates (K) used in the select stage of the Diffusion-DICE algorithm and the IDQL algorithm across different D4RL benchmark tasks. It shows that Diffusion-DICE requires significantly fewer action candidates than IDQL to achieve comparable performance.
read the caption
Table 3: Comparison of K between Diffusion-DICE and IDQL
🔼 This table presents the performance comparison of Diffusion-DICE against various baseline algorithms on 15 tasks from the D4RL benchmark. The results show the average normalized scores and standard deviations across 5 random seeds for each algorithm and task. Diffusion-DICE outperforms the other methods in a majority of tasks, highlighting its effectiveness, especially on more difficult tasks.
read the caption
Table 1: Evaluation results on D4RL benchmark. We report the average normalized scores at the end of training with standard deviation across 5 random seeds. Diffusion-DICE (D-DICE) demonstrates superior performance compared to all baseline algorithms in 13 out of 15 tasks, especially on more challenging tasks.

🔼 This table presents the performance comparison of Diffusion-DICE against various baseline algorithms on 15 tasks from the D4RL benchmark. The results, averaged across 5 random seeds, show the average normalized scores and standard deviations. Diffusion-DICE outperforms other methods on most tasks, particularly the more difficult ones.
read the caption
Table 1: Evaluation results on D4RL benchmark. We report the average normalized scores at the end of training with standard deviation across 5 random seeds. Diffusion-DICE (D-DICE) demonstrates superior performance compared to all baseline algorithms in 13 out of 15 tasks, especially on more challenging tasks.
Full paper#