↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat
TL;DR#
Generative models are usually trained to mimic human behavior, so it’s often assumed they can’t outperform the humans who created the data. This paper explores ’transcendence’, where a generative model surpasses the capabilities of its trainers. It focuses on the challenge of building models that achieve higher performance than the experts who created the training data. The issue is that using models to imitate humans typically limits them to the humans’ average performance.
This paper addresses this by demonstrating transcendence in a chess-playing AI called ChessFormer. The model was trained on game transcripts with a cap on the highest player rating in the training dataset. ChessFormer used low-temperature sampling which enables the model to effectively perform majority voting among various experts and thus achieve higher performance. The research team provides theoretical justification for this transcendence, along with experimental evidence and a discussion of broader implications.
Key Takeaways#
Why does it matter?#
This paper is crucial because it challenges the assumption that generative models can only match the performance of their human trainers. By demonstrating that a generative model can surpass its trainers in specific tasks, it opens up new avenues for research in areas like model ensembling and low-temperature sampling, potentially impacting various fields using similar techniques.
Visual Insights#

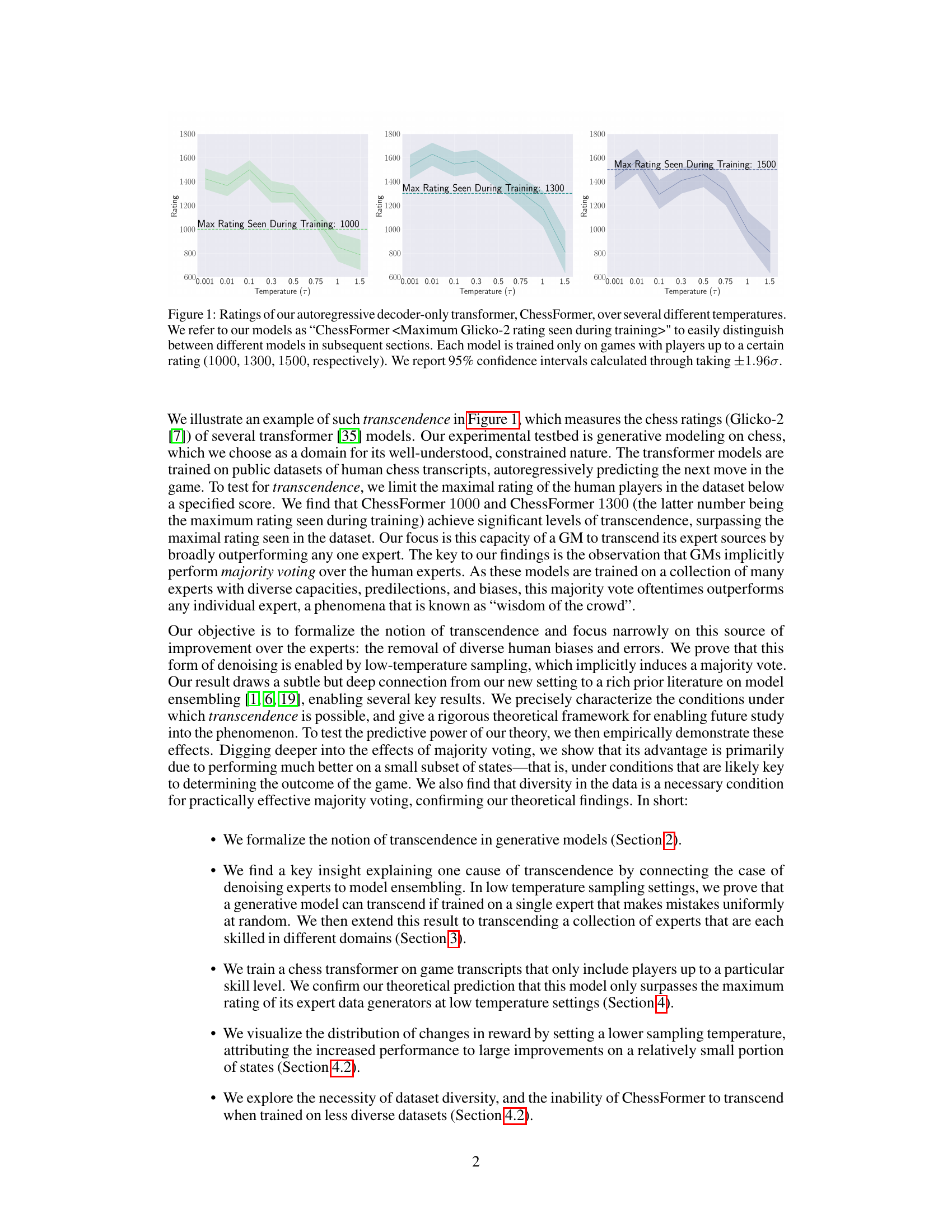
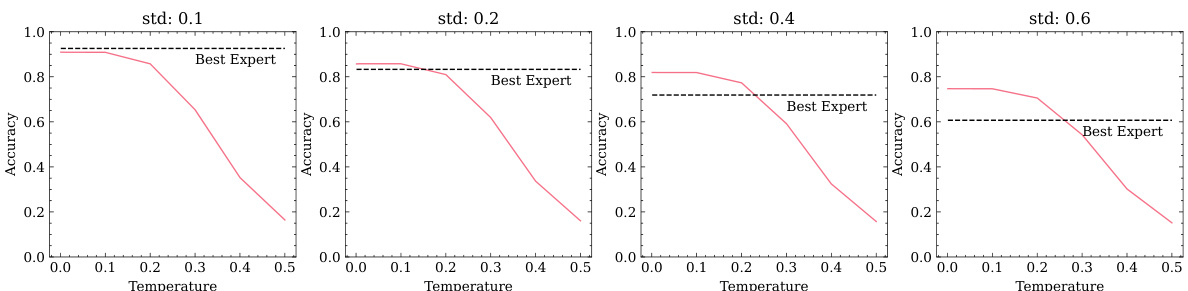
This figure shows the Glicko-2 ratings of several ChessFormer models trained on chess game transcripts with players up to a certain maximum rating (1000, 1300, and 1500). The x-axis represents the temperature used during sampling, and the y-axis represents the Glicko-2 rating. The shaded area represents the 95% confidence interval. The figure demonstrates the phenomenon of transcendence, where the model’s performance surpasses the maximum rating observed in the training data, especially at lower temperatures.

This table presents statistics that compare the performance of the ChessFormer model at different temperatures (τ = 0.001, 0.75, 1.0). It shows the expected reward (win probability), the improvement in reward compared to the baseline (τ = 1.0), and the top-k accuracy (percentage of games where the model’s move is among the top k best moves according to Stockfish). The results highlight the impact of temperature on model performance and support the concept of transcendence by showing improved performance at lower temperatures.
In-depth insights#
Transcendence Defined#
A theoretical framework for defining “transcendence” in generative models is crucial. It should move beyond simple imitation and focus on a model’s ability to outperform its training data’s creators in their original objectives. This necessitates a rigorous definition of performance metrics that goes beyond simple accuracy or cross-entropy loss. Dataset diversity and the mechanism of model learning (e.g., the role of temperature sampling, ensembling) also need explicit consideration. The definition should be robust enough to generalize across domains, avoiding overly specific metrics tied to a particular task or dataset. A clear delineation of “transcendence” helps distinguish genuine novel capabilities from overfitting or other artifacts of the training process. It’s essential to formally characterize conditions under which transcendence is possible, providing both theoretical and empirical validation.
Low-Temp Sampling#
The concept of ’low-temperature sampling’ emerges as a crucial technique in the paper, acting as a denoising mechanism for generative models. By reducing the temperature parameter in the softmax function, the model’s probability distribution becomes more sharply peaked around the highest probability actions. This effectively filters out the noise inherent in diverse expert datasets, allowing the model to converge on the most consistently optimal strategies, transcending the performance of individual experts in the training data. The theoretical underpinning for this involves the demonstration that low-temperature sampling induces an implicit ‘majority vote’ across experts. This majority vote, effectively aggregating diverse perspectives, allows the model to circumvent the shortcomings of individual human experts, leading to significantly improved performance. Experimentally, this was verified by observing a clear increase in the performance of chess models at low temperatures compared to higher-temperature settings, directly supporting the claim of transcendence.
ChessFormer: Experiment#
The ChessFormer experiment section would likely detail the methodology of training and evaluating the autoregressive transformer model designed to play chess. This would include a description of the dataset used, likely a large corpus of chess game transcripts from online platforms. The training process itself would be explained, focusing on the model architecture (likely a decoder-only transformer), the optimization algorithm (e.g., AdamW), and hyperparameters. Crucially, the evaluation methodology would be central, explaining how the model’s performance was measured – likely using a chess engine like Stockfish for rating comparisons against human players. The experimental design would aim to demonstrate transcendence, showing the model surpasses the playing abilities present within its training data. This would involve comparisons across different temperature settings to investigate the impact on performance and highlight any observed denoising effects resulting in improved decision-making. Ultimately, this section would present the empirical evidence supporting the paper’s claims regarding generative models exceeding the capabilities of the experts that trained them.
Dataset Diversity#
The concept of Dataset Diversity is crucial to the paper’s findings on model transcendence. The authors demonstrate that a lack of diversity hinders a model’s ability to surpass its training data experts. This is because diversity allows the model to learn from a broader range of strategies and approaches. When the model’s training data is limited in its variety, it is effectively learning from a noisy version of a single expert, which prevents it from achieving transcendence. Diversity acts as a form of denoising, removing idiosyncratic errors and biases present in individual experts’ games, thus leading to improved performance that exceeds any single expert in the dataset. The authors empirically support this by showing that models trained on more diverse datasets exhibit transcendence, while those trained on less diverse ones fail to transcend. This highlights the importance of data diversity in generative modeling, suggesting that careful curation and selection of diverse training data is key to unlocking a model’s full potential.
Future Directions#
Future research should explore extending the concept of transcendence beyond the narrow confines of chess and language models. Investigating diverse domains, such as computer vision and robotics, where expert human behavior is complex and nuanced, could reveal crucial insights into the conditions under which generative models surpass their creators. A particular focus should be placed on understanding the role of dataset diversity, proving theoretically and empirically whether diverse training data is a prerequisite for transcendence or merely a facilitator. Further exploration of the relationship between low-temperature sampling and majority voting is warranted, examining its generalizability to other types of generative models and objectives. Finally, it is crucial to address the ethical implications of models surpassing human capabilities. This includes developing strategies for responsible deployment and studying the potential for misuse or unintended consequences.
More visual insights#
More on figures

This figure shows how low temperature sampling affects the probability distribution of actions in a chess game. As the temperature (τ) decreases from 1.0 to 0.001, the model shifts its probability mass toward the high-reward move (trapping the queen with the rook). The opacity of the red arrows indicates the probability of each move, while the color of the squares represents the reward associated with moving a piece to that square. This illustrates the denoising effect of low-temperature sampling, where the model focuses on higher-reward actions.
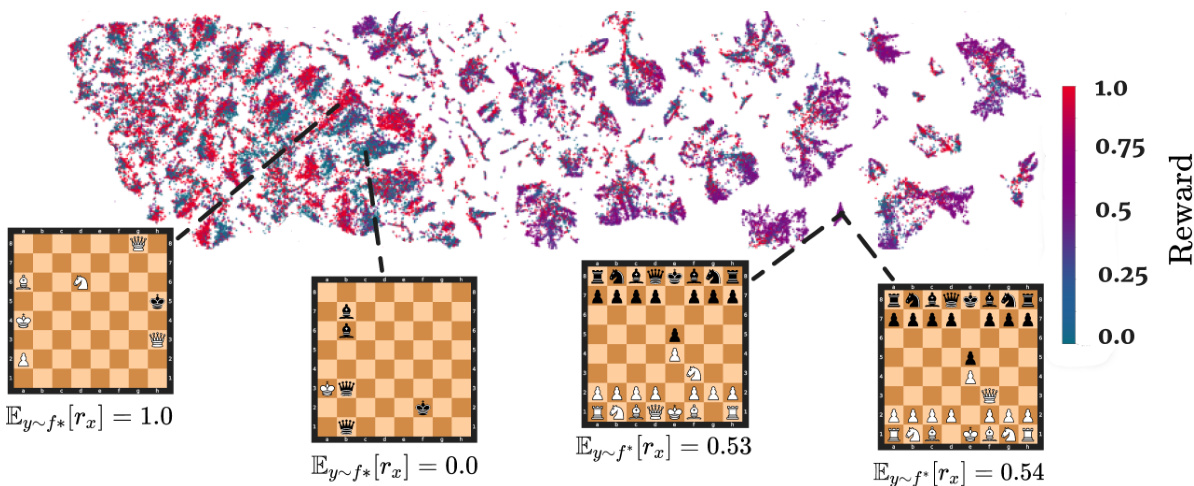
This figure visualizes the t-SNE embedding of ChessFormer’s last hidden layer latent representations of game transcripts during training. The color of each point represents the probability of winning (from Stockfish analysis), ranging from +1 (White wins) to 0 (Black wins). Four example board states are shown, illustrating how the model groups similar game states together in the latent space. The visualization shows that the model learns to distinguish between decisive endgame states and similar opening states.
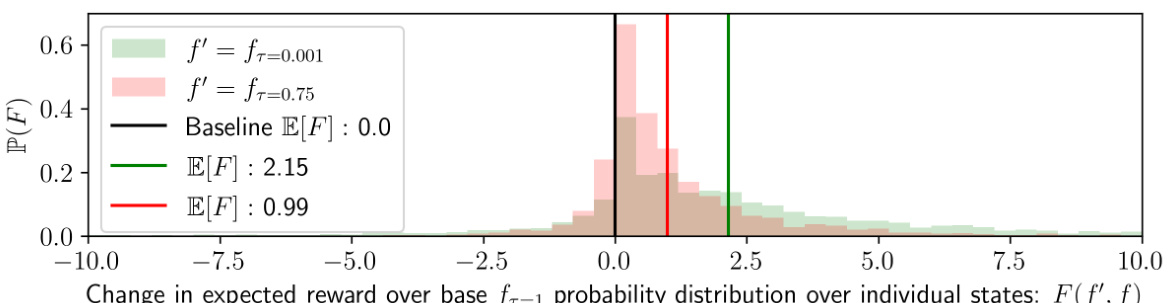
This figure visualizes how lowering the temperature in the ChessFormer model affects the expected reward. It shows the distribution of changes in expected reward (favor) when comparing low-temperature sampling (τ = 0.75 and τ = 0.001) to the baseline (τ = 1.0). The x-axis represents the change in expected reward, and the y-axis represents the probability of that change. The plot indicates that lower temperatures significantly increase the expected reward for a small subset of game states, while the effect on most states is minimal. This supports the idea that low-temperature sampling enhances the model’s performance by focusing improvements on key game states.
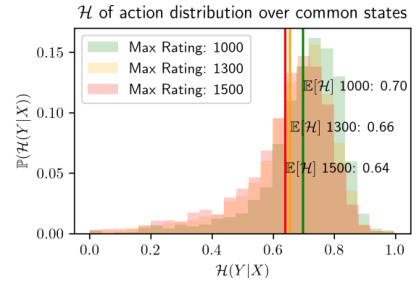
This figure shows the distribution of the normalized entropy of action distributions for different datasets. The x-axis represents the normalized entropy, and the y-axis represents the probability density. Three different datasets are used, each with a different maximum rating (1000, 1300, 1500). The average normalized entropy for each dataset is shown in the legend. The figure shows that the dataset with the maximum rating of 1000 has the highest average entropy, while the dataset with the maximum rating of 1500 has the lowest average entropy. This suggests that the dataset with the maximum rating of 1000 is the most diverse, while the dataset with the maximum rating of 1500 is the least diverse. The figure supports the claim that dataset diversity is essential for transcendence.

This figure shows the Glicko-2 ratings of several transformer models trained to play chess, each trained on game transcripts with players up to a maximum rating (1000, 1300, and 1500). The x-axis represents the temperature used during sampling, and the y-axis shows the resulting rating. The figure demonstrates the phenomenon of transcendence, where the model surpasses the maximum rating of the human players in its training data at lower temperatures (higher certainty). The confidence intervals shown highlight the statistical significance of these results.
This figure shows the chess ratings (Glicko-2) of several transformer models trained on human chess transcripts with maximum player ratings capped at 1000, 1300, and 1500. The x-axis represents the temperature used during sampling, and the y-axis represents the Glicko-2 rating. The figure demonstrates the phenomenon of ’transcendence,’ where the models outperform the maximum rating observed in their training data, especially at lower temperatures.

This figure demonstrates how low temperatures affect the model’s action selection in chess. As the temperature (τ) decreases, the model becomes more deterministic, focusing probability mass on higher-reward actions, such as trapping the queen. This showcases the denoising effect of low-temperature sampling, where less likely, lower-reward actions (moves) are suppressed.

This figure shows how the probability distribution over possible moves changes with temperature. As the temperature decreases (τ goes from 1.0 to 0.001), the probability mass shifts towards the highest reward move (trapping the queen with the rook). The opacity of the red arrows indicates the probability of each move, and the color of the squares represents the reward associated with that move.

This figure visualizes how low temperature sampling affects the probability distribution of actions in a chess game. As the temperature decreases from 1.0 to 0.001, the model’s probability mass shifts towards higher-reward moves, demonstrating the denoising effect of low temperature. The visualization uses arrows and colored squares to represent the probability of each move and the associated rewards, respectively. This illustrates how low temperature sampling helps the model focus on actions with higher expected rewards, effectively mitigating noise and improving decision making.
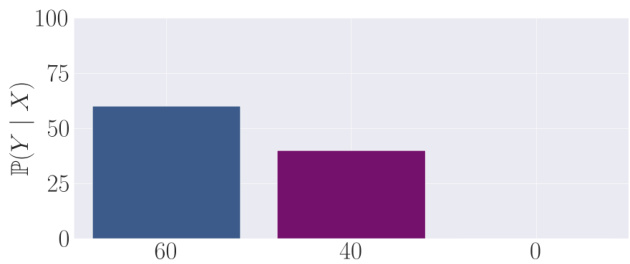
This figure shows a toy example of probability distribution of an expert’s output. The x-axis represents the output options (actions), while the y-axis represents the probability of selecting each output. There are three options: a low-reward action (left), a high-reward action (purple, center), and another low-reward action (right). The expert’s distribution shows a relatively low probability (around 60%) for selecting the high-reward action, with most of the probability mass allocated to the low-reward actions.
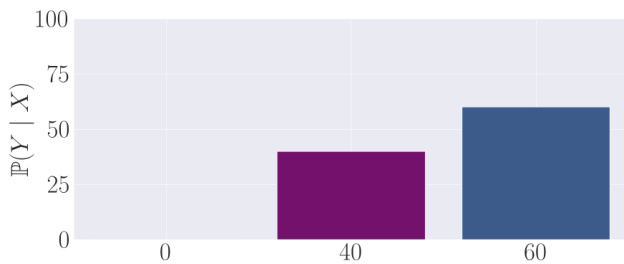
This figure is a bar chart showing the probability distribution of an expert’s output for a given input. The x-axis represents possible outputs (actions), and the y-axis shows the probability of selecting each output. The chart reveals that while the expert assigns a non-negligible probability to the high-reward action (represented in purple), it predominantly selects low-reward actions. This illustrates a scenario where an individual expert makes frequent mistakes, a point crucial to understanding the paper’s concept of transcendence.
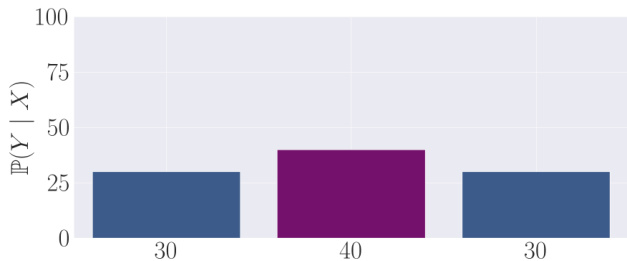
This figure is a bar chart showing the probability distribution of three possible outputs (actions) from two different experts. Expert 1 and Expert 2 each have probability distributions that show the probabilities for each action. The probability for the correct action is higher in both distributions, but not overwhelmingly so. By averaging the probabilities of Expert 1 and Expert 2, a new distribution is created where the probability of the correct action is significantly higher than the probabilities for the incorrect actions. This illustrates how averaging the outputs of multiple experts can increase the probability of selecting the correct action. This visualization supports the claim that low-temperature sampling, a technique used in generative models, allows models to select the output with highest probability by implicitly performing a majority vote between different experts.
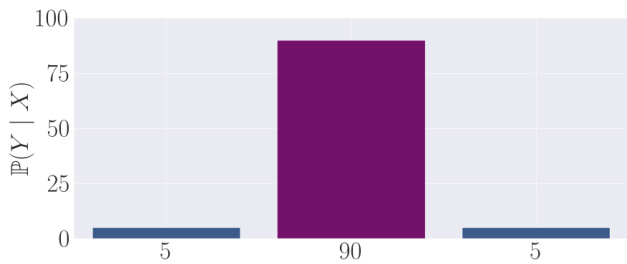
This figure shows how low-temperature sampling leads to higher expected rewards. It visualizes a simplified scenario with three possible actions: two poor actions with low rewards (5%) and one optimal action with a high reward (90%). As the temperature decreases, more weight is given to the high-reward action, thus increasing the overall expected reward. This illustrates the concept of transcendence, where the generative model’s performance surpasses that of individual experts due to low-temperature sampling effectively performing a majority vote.
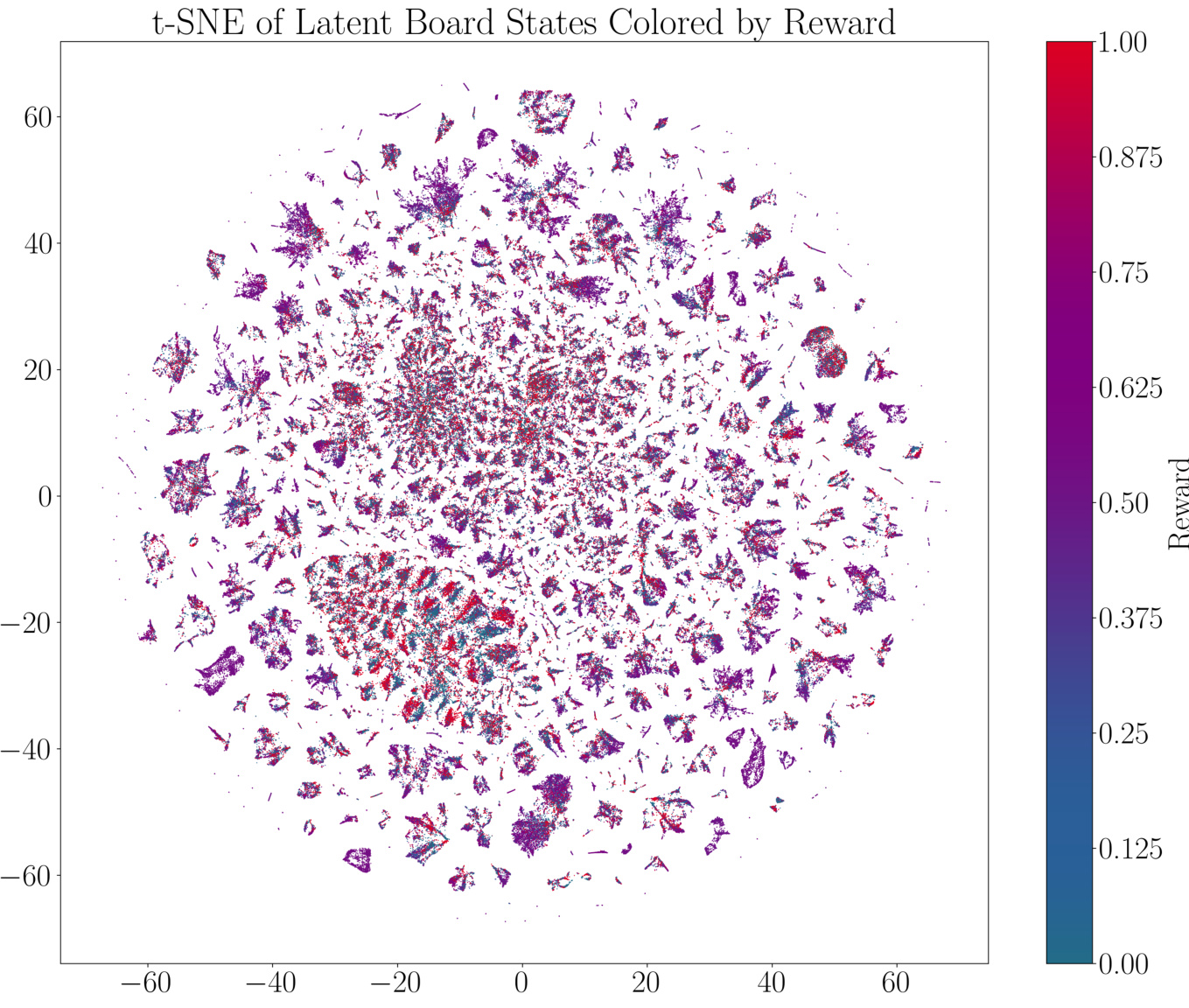
This figure visualizes a t-SNE embedding of the last hidden layer’s latent representations from ChessFormer during training. The color represents the probability of winning (from Stockfish analysis), showing how the model represents game states. Several example board states are shown alongside their clusters and expected rewards based on Stockfish’s distribution. The model is able to differentiate between states with determined outcomes and extremely similar opening states.

The figure shows the chess ratings (Glicko-2) of several transformer models trained on human chess transcripts with different maximum player rating cutoffs (1000, 1300, and 1500). Each model’s performance is evaluated at various temperatures, illustrating the phenomenon of transcendence, where the model surpasses the skill level of the experts in its training data. The 95% confidence intervals highlight the statistical significance of the results.
Full paper#