TL;DR#
Graph Neural Networks (GNNs) often suffer from over-squashing (information loss from distant nodes due to bottlenecks) and over-smoothing (nodes becoming indistinguishable after multiple aggregation layers). Existing solutions often focus on adding edges to address over-squashing but can exacerbate over-smoothing. This paper challenges this approach.
The research introduces a novel spectral-based edge pruning technique, leveraging the Braess paradox which shows that removing edges can sometimes improve performance. This method, PROXYDELETE, efficiently optimizes the spectral gap to alleviate both problems simultaneously. Experiments demonstrate improved GNN performance, particularly in heterophilic graphs. The findings also link spectral gap optimization to the concept of graph lottery tickets, suggesting that pruning can create sparse, high-performing subnetworks.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses the prevalent over-squashing and over-smoothing issues in Graph Neural Networks (GNNs). By proposing a novel spectral-based edge pruning method, it offers a computationally efficient solution to improve GNN generalization, particularly in heterophilic settings. Furthermore, it establishes a connection between spectral gap optimization and graph lottery tickets, opening new avenues for research in GNN optimization and model sparsification.
Visual Insights#

🔼 This figure demonstrates the Braess paradox in the context of graph neural networks. It shows four graphs (G, G+, G-, G~) illustrating how deleting or adding an edge can impact the spectral gap, a key factor in over-squashing and over-smoothing. Graph G- shows that removing an edge can paradoxically increase the spectral gap, unlike common assumptions. The graphs G+ and G~ illustrate the trade-off between over-squashing and over-smoothing when adding edges.
read the caption
Figure 1: Braess' paradox. We derive a simple example where deleting an edge from G to obtain G- yields a higher spectral gap. Alternatively, we add a single edge to the base graph to either increase (G+) or to decrease (G+) the spectral gap. The relationship between the four graphs is highlighted by arrows when an edge is added/deleted.
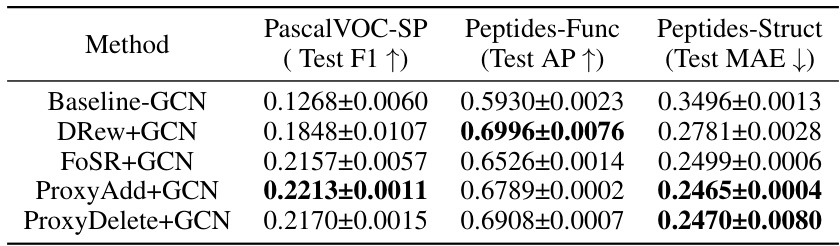
🔼 This table presents the results of the Long Range Graph Benchmark (LRGB) experiments. The LRGB is designed to specifically test graph neural networks (GNNs) for over-squashing. The table compares several methods including a baseline GCN, DRew (a graph rewiring method), FoSR (another graph rewiring method focused on spectral gap expansion), and the authors’ proposed methods (ProxyAdd and ProxyDelete). The results are shown for three datasets (PascalVOC-SP, Peptides-Func, and Peptides-Struct) and three metrics (Test F1, Test AP, and Test MAE). Each metric measures a different aspect of GNN performance on the datasets.
read the caption
Table 1: Results on Long Range Graph Benchmark datasets.
In-depth insights#
Spectral Rewiring#
Spectral rewiring, a technique to enhance graph neural networks (GNNs), focuses on modifying a graph’s structure to optimize its spectral properties. It tackles the dual challenges of over-squashing and over-smoothing that often hinder GNN performance. Over-squashing, caused by topological bottlenecks, limits information flow; while over-smoothing leads to indistinguishable node representations. Spectral rewiring offers a solution by strategically adding or removing edges to improve the spectral gap, a key indicator of a graph’s connectivity. The Braess paradox inspired an innovative approach, demonstrating that edge removal can sometimes improve information flow, challenging conventional wisdom. This counter-intuitive strategy, combined with efficient spectral gap optimization techniques, enables fine-tuned control over information diffusion in GNNs, resulting in improved generalization and reduced computational costs. By connecting spectral optimization to graph pruning, spectral rewiring also paves the way for efficient training and identification of ‘winning’ subnetworks, advancing both the theoretical understanding and practical application of GNNs.
Braess Paradox in GNNs#
The Braess paradox, originally observed in traffic networks, reveals that adding edges to a graph can paradoxically decrease its overall efficiency. In Graph Neural Networks (GNNs), this translates to the possibility that adding connections between nodes might hinder, rather than improve, the flow of information. This is particularly relevant in the context of GNN over-squashing and over-smoothing. Over-squashing occurs when information from distant nodes fails to propagate effectively due to topological bottlenecks. Over-smoothing, conversely, happens when repeated aggregation layers cause node representations to converge, losing their discriminative power. The Braess paradox in GNNs suggests that intuitively beneficial edge additions, intended to alleviate over-squashing, might inadvertently worsen over-smoothing, highlighting the complex interplay between network topology and GNN performance. Therefore, understanding and addressing the Braess paradox is crucial for designing effective GNN architectures, and may involve novel pruning strategies that selectively remove edges to optimize information flow and avoid the detrimental effects of both over-squashing and over-smoothing.
Over-Squashing & Smoothing#
Over-squashing and over-smoothing are two significant challenges in graph neural networks (GNNs). Over-squashing occurs when information from distant nodes fails to propagate effectively due to topological bottlenecks, hindering the model’s ability to capture long-range dependencies. Conversely, over-smoothing arises from repeated aggregation steps, causing node representations to converge and lose their distinctiveness. These phenomena are not always diametrically opposed, as edge deletions can mitigate both simultaneously. The Braess paradox, where removing edges can improve the overall information flow, provides a theoretical basis for this counter-intuitive result. Spectral gap maximization, often pursued through edge additions to combat over-squashing, can exacerbate over-smoothing. Therefore, a more nuanced approach is needed that selectively adds or removes edges to optimize both objectives, possibly leading to more generalizable and efficient GNN architectures.
Proxy Spectral Gap#
The concept of “Proxy Spectral Gap” in graph neural network (GNN) optimization suggests a computationally efficient method to approximate the spectral gap, a crucial factor influencing GNN performance. Instead of directly calculating the spectral gap, which is computationally expensive for large graphs, this approach uses a proxy function. This proxy likely involves leveraging matrix perturbation theory or similar techniques to estimate the change in eigenvalues caused by adding or deleting an edge. By utilizing this proxy, the algorithm can efficiently rank edges based on their potential impact on the spectral gap, thus enabling faster graph sparsification or rewiring. The accuracy of this proxy is critical, as its effectiveness directly affects the algorithm’s ability to optimize the spectral gap and improve GNN generalization. While computationally efficient, a potential trade-off might be a slight loss of precision in identifying the optimal edge modifications compared to a direct spectral gap calculation. Further investigation is needed to analyze the balance between computational speed and the accuracy of the proxy in various graph structures and sizes.
Graph Lottery Tickets#
The concept of “Graph Lottery Tickets” cleverly merges the “lottery ticket hypothesis” from deep learning with graph neural networks (GNNs). It posits that sparse sub-networks (winning tickets), carefully selected from a larger, dense GNN, can achieve comparable or even better performance on graph-related tasks. This offers potential benefits in terms of reduced computational cost and improved generalization. The research explores how techniques like spectral gap optimization and edge pruning can aid in identifying these winning tickets. The intriguing connection to over-squashing and over-smoothing in GNNs is highlighted, showing that addressing these issues through graph sparsification can simultaneously lead to more efficient and effective models. Finding data-agnostic criteria for pruning is a key challenge, with spectral gap-based methods offering a promising approach to this problem.
More visual insights#
More on figures

🔼 This figure demonstrates the Braess paradox in the context of graph neural networks. It shows four graphs (G, G-, G+, ~G+) illustrating how removing an edge (G-) can improve the spectral gap, which is related to over-squashing, while adding an edge (G+) can either improve or worsen the spectral gap, thus potentially resulting in over-smoothing. The figure highlights that simply adding edges to mitigate over-squashing may not always be beneficial, demonstrating a trade-off between over-squashing and over-smoothing.
read the caption
Figure 1: Braess' paradox. We derive a simple example where deleting an edge from G to obtain G- yields a higher spectral gap. Alternatively, we add a single edge to the base graph to either increase (G+) or to decrease (~G+) the spectral gap. The relationship between the four graphs is highlighted by arrows when an edge is added/deleted.
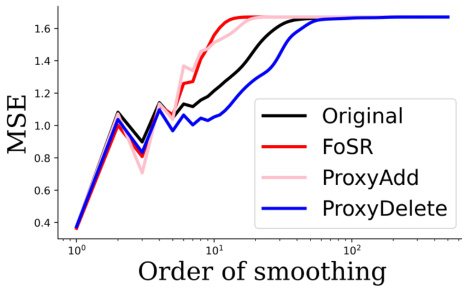
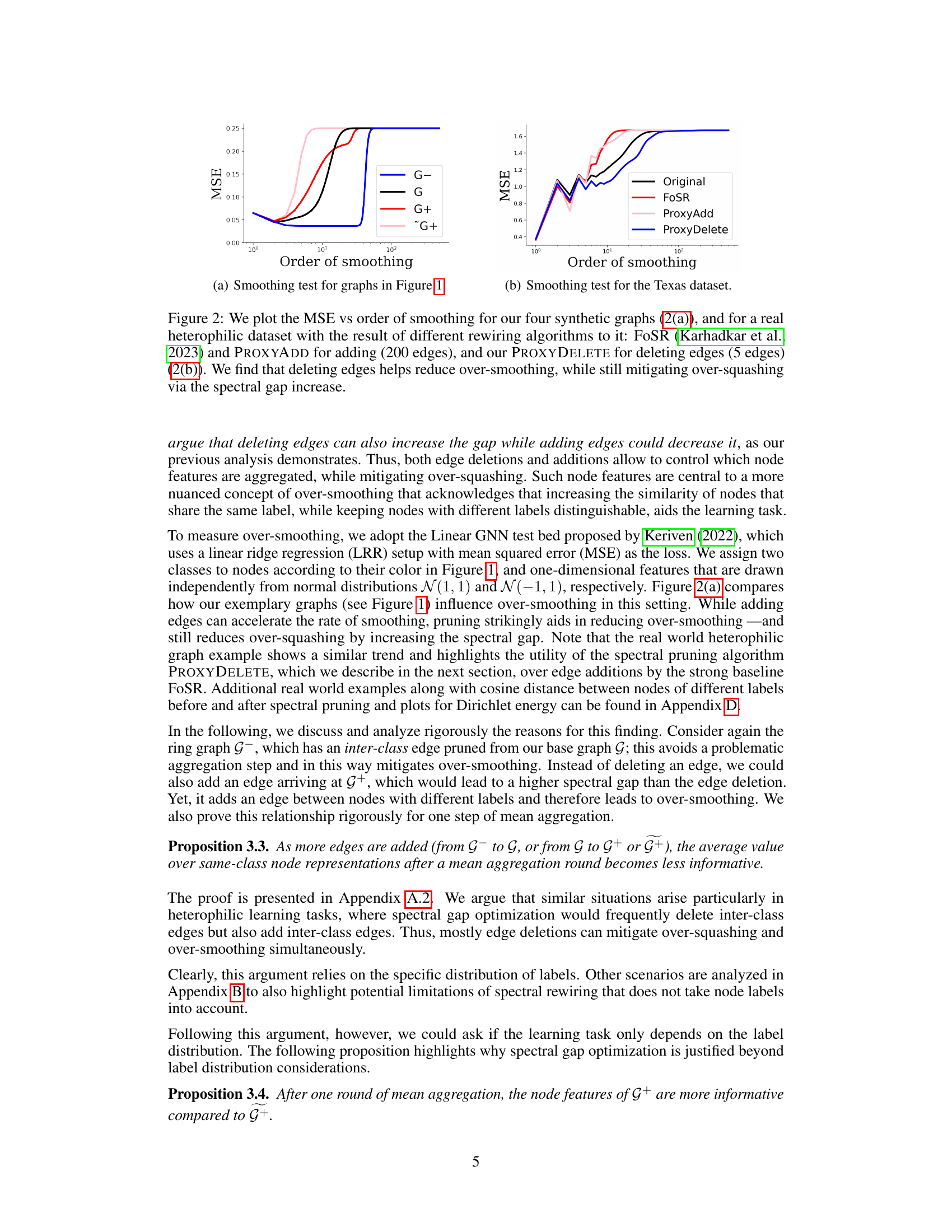
🔼 This figure compares the mean squared error (MSE) against the order of smoothing for different graph rewiring algorithms. Subfigure (a) shows results for four synthetic graphs illustrating the Braess paradox, where edge deletion surprisingly improves the spectral gap and reduces over-smoothing. Subfigure (b) demonstrates these effects on a real heterophilic dataset, showing that PROXYDELETE (edge deletion) outperforms FoSR (edge addition) in mitigating over-smoothing while also addressing over-squashing.
read the caption
Figure 2: We plot the MSE vs order of smoothing for our four synthetic graphs (2(a)), and for a real heterophilic dataset with the result of different rewiring algorithms to it: FoSR (Karhadkar et al., 2023) and PROXYADD for adding (200 edges), and our PROXYDELETE for deleting edges (5 edges) (2(b)). We find that deleting edges helps reduce over-smoothing, while still mitigating over-squashing via the spectral gap increase.

🔼 This figure illustrates Braess’s paradox in the context of spectral graph theory. It demonstrates how removing an edge (G-) from a graph (G) can surprisingly increase the spectral gap, which is a measure of how well-connected the graph is. Conversely, adding an edge can either improve (G+) or worsen (G+ )the spectral gap, highlighting the non-monotonic relationship between edge additions/deletions and the spectral gap. This counter-intuitive behavior shows that simply maximizing spectral gap by adding edges isn’t always the best strategy and that edge deletions also have a role in optimizing graph structure.
read the caption
Figure 1: Braess' paradox. We derive a simple example where deleting an edge from G to obtain G- yields a higher spectral gap. Alternatively, we add a single edge to the base graph to either increase (G+) or to decrease (G+) the spectral gap. The relationship between the four graphs is highlighted by arrows when an edge is added/deleted.

🔼 This figure demonstrates the Braess paradox in the context of spectral graph theory. It shows how removing an edge (G-) from a graph (G) can increase its spectral gap, which is a measure of connectivity and is related to over-squashing in graph neural networks. Adding an edge can either improve or worsen the spectral gap depending on its placement (G+ and G+). This illustrates that over-squashing and over-smoothing in graph neural networks might not always be diametrically opposed, and that edge deletions can be beneficial.
read the caption
Figure 1: Braess' paradox. We derive a simple example where deleting an edge from G to obtain G- yields a higher spectral gap. Alternatively, we add a single edge to the base graph to either increase (G+) or to decrease (G+) the spectral gap. The relationship between the four graphs is highlighted by arrows when an edge is added/deleted.
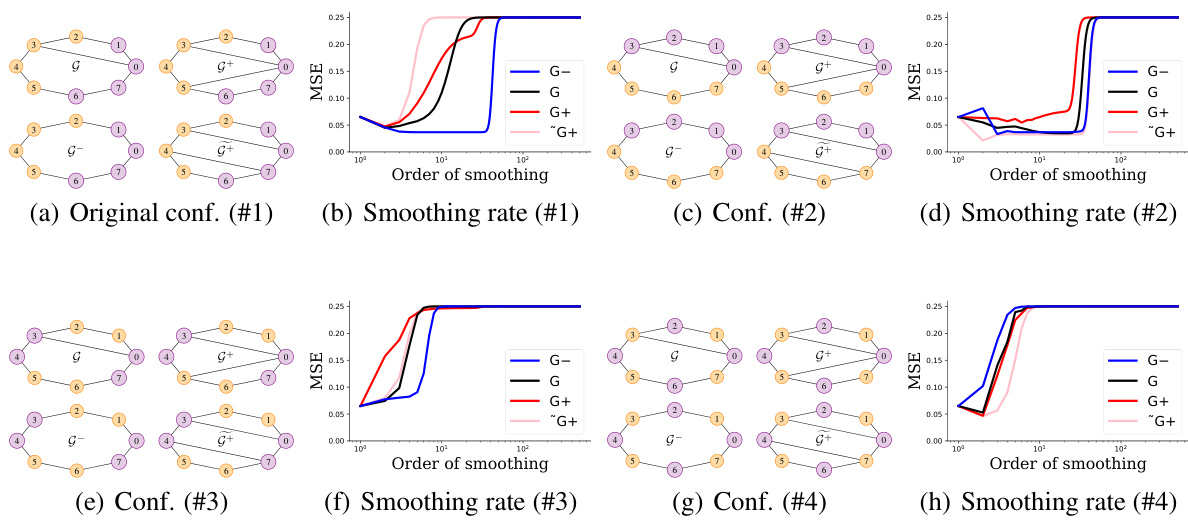
🔼 This figure demonstrates the Braess paradox in the context of spectral graph theory. It shows how removing an edge (G-) from a small graph can paradoxically increase the spectral gap (a measure of how well information flows through the graph), while adding edges (G+ and G++) can either increase or decrease it, depending on the placement of the added edge. This highlights the non-intuitive relationship between graph structure and spectral properties and suggests that simply adding edges to improve information flow isn’t always the optimal strategy.
read the caption
Figure 1: Braess' paradox. We derive a simple example where deleting an edge from G to obtain G- yields a higher spectral gap. Alternatively, we add a single edge to the base graph to either increase (G+) or to decrease (G+) the spectral gap. The relationship between the four graphs is highlighted by arrows when an edge is added/deleted.
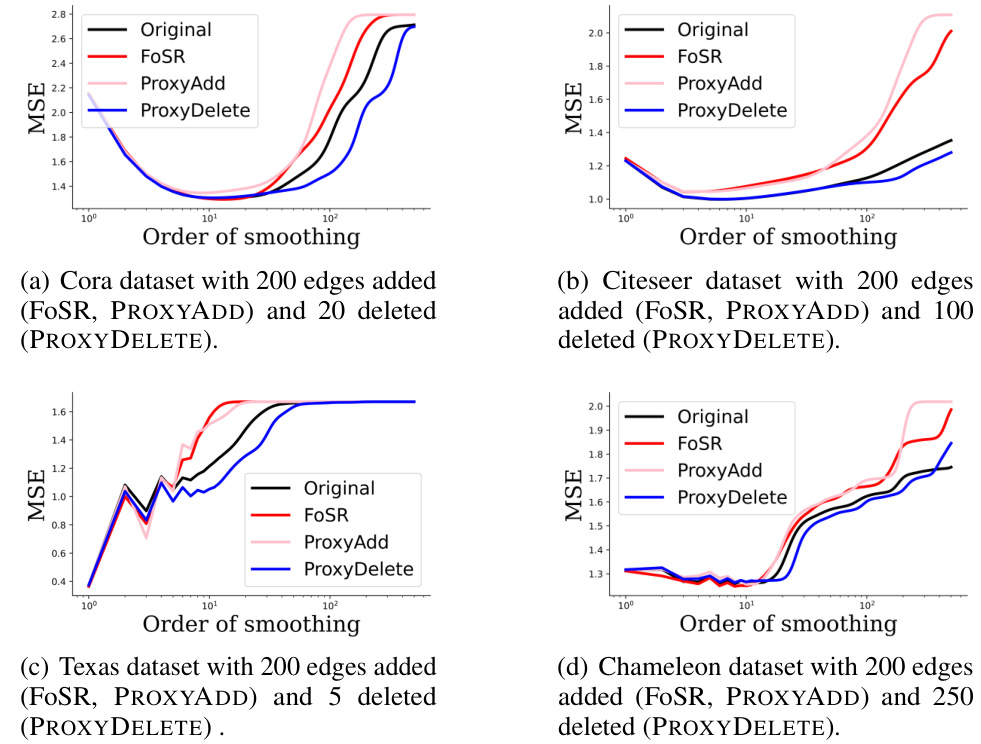
🔼 This figure displays the Mean Squared Error (MSE) versus the order of smoothing for four real-world datasets: Cora, Citeseer, Texas, and Chameleon. Each dataset is shown with its original graph and after applying three different graph rewiring methods: FoSR (for adding edges), PROXYADD (for adding edges), and PROXYDELETE (for deleting edges). The results demonstrate that PROXYDELETE, the spectral pruning method, effectively mitigates over-squashing (by increasing the spectral gap) and simultaneously slows down the rate of over-smoothing, especially in heterophilic datasets (Texas and Chameleon).
read the caption
Figure 6: We show on real-world graphs that spectral pruning can not only mitigate over-squashing by improving the spectral gap but also slows down the rate of smoothing, thus effectively preventing over-smoothing as well.

🔼 This figure shows the Mean Squared Error (MSE) against the order of smoothing for different graph rewiring methods. The left subplot (2(a)) demonstrates the results for four synthetic graphs created using Braess’s paradox, illustrating how edge deletions can decrease over-smoothing while simultaneously improving the spectral gap (mitigating over-squashing). The right subplot (2(b)) presents findings for the Texas dataset, comparing PROXYADD (edge addition), PROXYDELETE (edge deletion), and FoSR (another edge addition method) against a baseline GCN, emphasizing that deleting edges via PROXYDELETE is particularly effective in reducing over-smoothing while maintaining good performance.
read the caption
Figure 2: We plot the MSE vs order of smoothing for our four synthetic graphs (2(a)), and for a real heterophilic dataset with the result of different rewiring algorithms to it: FoSR (Karhadkar et al., 2023) and PROXYADD for adding (200 edges), and our PROXYDELETE for deleting edges (5 edges) (2(b)). We find that deleting edges helps reduce over-smoothing, while still mitigating over-squashing via the spectral gap increase.
🔼 This figure illustrates the Braess paradox in the context of graph neural networks. It demonstrates how removing an edge (G-) can surprisingly improve the spectral gap, which is a measure of network efficiency. Conversely, adding edges (G+ and G++) can either increase or decrease the spectral gap, highlighting the complex relationship between graph structure and network efficiency. This example showcases that edge deletions are not necessarily detrimental and can be effective in mitigating over-squashing and over-smoothing, both known limitations of message-passing graph neural networks. The four graphs show a scenario where removing an edge (G-) increases the spectral gap and helps reduce over-squashing and over-smoothing simultaneously.
read the caption
Figure 1: Braess' paradox. We derive a simple example where deleting an edge from G to obtain G- yields a higher spectral gap. Alternatively, we add a single edge to the base graph to either increase (G+) or to decrease (G+) the spectral gap. The relationship between the four graphs is highlighted by arrows when an edge is added/deleted.
More on tables
🔼 This table presents the results of the proposed spectral graph pruning methods (PROXYADD and PROXYDELETE), along with existing baseline methods (Baseline-GCN, DRew+GCN, and FoSR+GCN) on three datasets from the Long Range Graph Benchmark: PascalVOC-SP (node classification), Peptides-Func (graph classification), and Peptides-Struct (graph regression). The metrics reported are Test F1 (for PascalVOC-SP), Test AP (for Peptides-Func), and Test MAE (for Peptides-Struct). The table shows the effectiveness of the proposed methods in improving performance compared to baselines, particularly in mitigating over-squashing and over-smoothing.
read the caption
Table 1: Results on Long Range Graph Benchmark datasets.

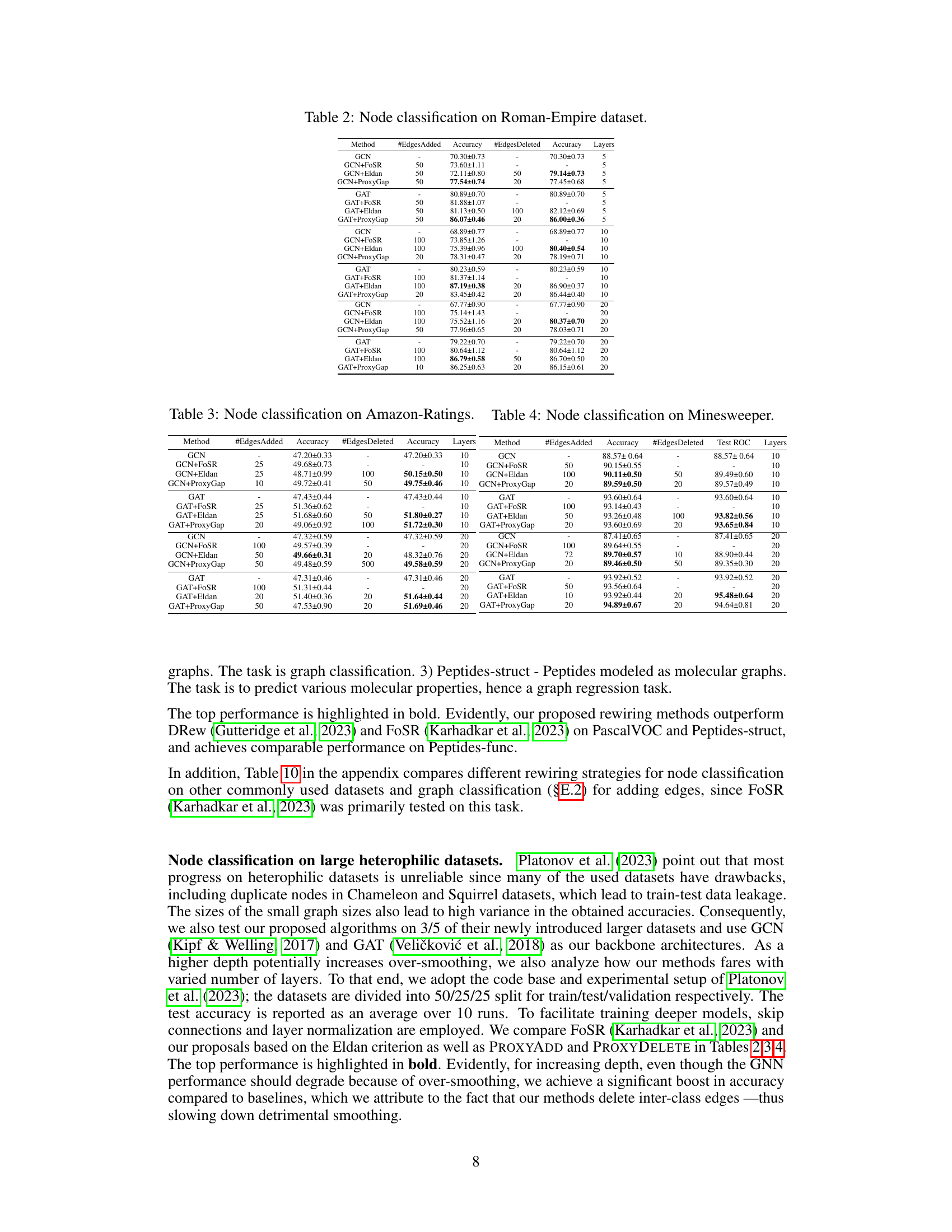
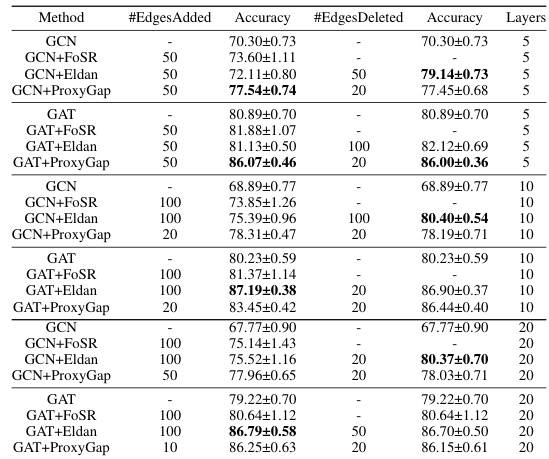
🔼 The table presents the results of node classification experiments on the Roman-Empire dataset using GCN and GAT models with different numbers of layers and edge modifications. For each model and layer configuration, the table shows the number of edges added or deleted using different methods (FoSR, Eldan, ProxyGap), the resulting accuracy, and the standard deviation of the accuracy across multiple runs. The results are compared with a baseline GCN/GAT model without any edge modifications. This table allows assessing the impact of the edge rewiring algorithms on the performance of the GCN and GAT models for node classification tasks on a specific dataset.
read the caption
Table 2: Node classification on Roman-Empire dataset.

🔼 This table presents the results of experiments on graph lottery tickets. It compares the performance of three different pruning methods: Unified Graph Sparsification (UGS), ELDANDELETE pruning, and PROXYDELETE pruning. The table shows the graph sparsity (GS), weight sparsity (WS), and accuracy (Acc) achieved by each method on three different datasets: Cora, Citeseer, and Pubmed.
read the caption
Table 5: Pruning for lottery tickets comparing UGS to our ELDANDELETE pruning and our PROXY-DELETE pruning. We report Graph Sparsity (GS), Weight Sparsity (WS), and Accuracy (Acc).

🔼 This table compares the results of Eldan’s criterion and two proxy methods (APROXYDELETE and APROXYADD) for predicting the change in the spectral gap (Δλ₁) after adding or deleting an edge in the toy graph examples shown in Figure 1. Eldan’s criterion provides a theoretical guarantee for the sign of the spectral gap change, while the proxy methods offer computationally efficient approximations. The table shows that the proxy methods accurately predict the sign of Δλ₁ in most cases, demonstrating their effectiveness in approximating the spectral gap change.
read the caption
Table 6: Computationally calculated criteria for the toy graph examples.

🔼 This table presents the results of the Long Range Graph Benchmark (LRGB) experiments. The LRGB is a benchmark specifically designed to assess the performance of Graph Neural Networks (GNNs) in addressing over-squashing. The table compares the performance of various methods (a baseline GCN and GCNs combined with different graph rewiring techniques: DRew, FoSR, ProxyAdd, and ProxyDelete) on three different datasets (PascalVOC-SP, Peptides-Func, and Peptides-Struct) and across three evaluation metrics (Test F1, Test AP, and Test MAE) relevant to the specific task of each dataset (node classification, link prediction, and graph classification). The results highlight the effectiveness of the proposed spectral gap-based edge deletion and addition methods (ProxyDelete and ProxyAdd) in improving GNN performance on these challenging datasets.
read the caption
Table 1: Results on Long Range Graph Benchmark datasets.

🔼 This table presents the cosine distance between nodes with different labels for six datasets (Cornell, Wisconsin, Texas, Chameleon, Squirrel, and Actor) before training, after training on the original graph, and after training on a graph pruned using the PROXYDELETE method. The results show that the cosine distance increases after pruning, indicating that the method effectively prevents over-smoothing by preserving the distinguishability of nodes with different labels.
read the caption
Table 9: Cosine distance between nodes of different labels before and after deleting edges using PROXYDELETE.
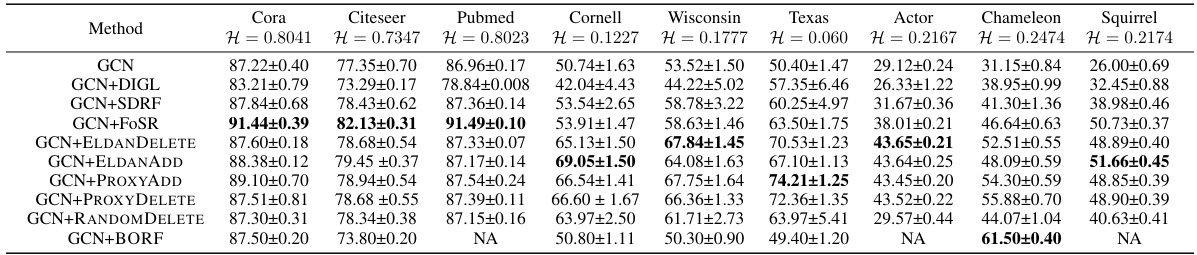
🔼 The table presents the results of the proposed methods and baselines on three datasets from the Long Range Graph Benchmark (LRGB). The datasets represent different graph structures and tasks (node classification and graph classification). The metrics used are F1 score, Average Precision (AP), and Mean Absolute Error (MAE), reflecting performance on different graph-level prediction tasks. The baseline GCN model is compared against several variants incorporating graph rewiring techniques, demonstrating their impact on overall prediction accuracy. This shows the effectiveness of the proposed spectral graph pruning method compared to other existing state-of-the-art approaches on real-world data.
read the caption
Table 1: Results on Long Range Graph Benchmark datasets.

🔼 This table compares the performance of Graph Convolutional Networks (GCNs) combined with three different graph rewiring methods on graph classification tasks. The methods compared are FoSR (First-order spectral rewiring), ELDANADD (Eldan’s criterion-based edge addition), and PROXYADD (proxy spectral gap-based edge addition). The table shows the accuracy achieved by each method on six different datasets (ENZYMES, MUTAG, IMDB-BINARY, REDDIT-BINARY, COLLAB, PROTEINS). The results demonstrate the effectiveness of the proposed ELDANADD and PROXYADD methods in improving the accuracy of GCNs on graph classification tasks, often outperforming FoSR.
read the caption
Table 11: Graph classification with GCN comparing FoSR, ELDANADD and PROXYADD.

🔼 This table compares the performance of Graph Convolutional Networks (GCNs) combined with different graph rewiring methods on graph classification tasks. The methods compared are FoSR (First-order spectral rewiring), ELDANADD (Eldan’s criterion-based edge addition), and PROXYADD (proxy spectral gap-based greedy graph addition). The table shows the accuracy achieved by each method on several benchmark datasets (ENZYMES, MUTAG, IMDB-BINARY, REDDIT-BINARY, COLLAB, PROTEINS). The results highlight the relative performance of the different graph rewiring techniques in improving graph classification accuracy.
read the caption
Table 11: Graph classification with GCN comparing FoSR, ELDANADD and PROXYADD.

🔼 This table presents the results of node classification experiments using Relational-GCNs on nine datasets. Three different graph rewiring methods are compared: FoSR (First-order Spectral Rewiring), a method based on Eldan’s criterion, and the authors’ proposed PROXYADD method. The table shows the accuracy achieved by each method on each dataset, highlighting the performance differences between the approaches.
read the caption
Table 13: Node classification using Relational-GCNs comparing FoSR, Eldan's criterion and PROXYADD.
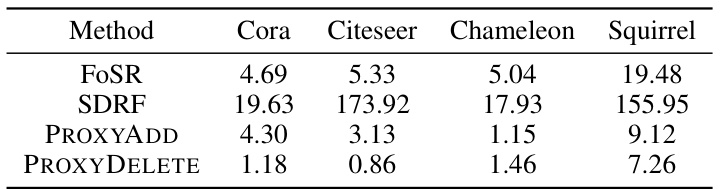
🔼 This table presents the runtimes, in seconds, for modifying 50 edges in four different graph datasets using four different methods: FoSR, SDRF, PROXYADD, and PROXYDELETE. The runtimes are broken down by dataset (Cora, Citeseer, Chameleon, and Squirrel) and method. The table shows that PROXYDELETE is consistently the fastest method, with runtimes significantly lower than the other three methods, especially on larger datasets like Chameleon and Squirrel. This highlights the computational efficiency of the PROXYDELETE method compared to alternative approaches for spectral graph rewiring.
read the caption
Table 14: Runtimes for 50 edge modifications in seconds.

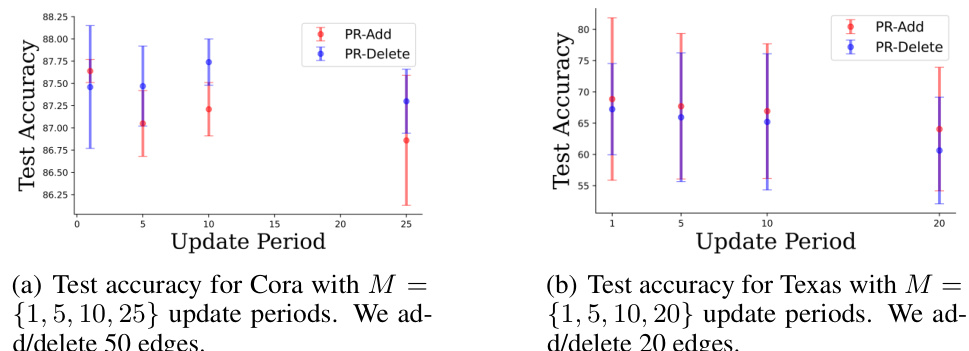
🔼 This table compares the runtimes (RT) of the PROXYADD and PROXYDELETE algorithms with different update periods (M) for modifying 50 edges in four different datasets (Cora, Citeseer, Chameleon, Squirrel). It also shows the spectral gap before (SG.B) and after (SG.A) the rewiring process. The results demonstrate the trade-off between runtime and the spectral gap improvement achieved by varying the update frequency.
read the caption
Table 15: Empirical runtime (RT) comparisons with different update periods for the criterion for 50 edges. We also report the spectral gap before (SG.B) and after rewiring (SG.A).

🔼 This table compares the effectiveness of different graph rewiring methods in improving the spectral gap. It shows the spectral gap before and after applying FoSR, PROXYADD, PROXYDELETE, ELDANADD, and ELDANDELETE methods. The results demonstrate that PROXYADD and PROXYDELETE significantly improve the spectral gap compared to FoSR.
read the caption
Table 16: We compare the spectral gap improvements of different rewiring methods for 50 edge modifications. From the table it is evident that our proposed PROXYADD and PROXYDELETE methods improve the spectral gap much better than FoSR.

🔼 The table presents the results of experiments conducted on the Long Range Graph Benchmark datasets. Several GCN models are compared, including a baseline GCN and models augmented with different graph rewiring techniques: DRew, FoSR, ProxyAdd, and ProxyDelete. The performance of each model is evaluated using three metrics: Test F1 (for PascalVOC-SP), Test AP (for Peptides-Func), and Test MAE (for Peptides-Struct). The results show the effectiveness of the proposed spectral gap-based edge addition and deletion methods (ProxyAdd and ProxyDelete) in improving the performance of GCNs on these datasets.
read the caption
Table 1: Results on Long Range Graph Benchmark datasets.

🔼 This table presents the results of the proposed spectral graph pruning methods (PROXYADD and PROXYDELETE) and compares them to several baselines on three datasets from the Long Range Graph Benchmark (LRGB). The datasets represent different node classification and graph classification tasks. The metrics used for evaluation include F1-score (for classification tasks) and Average Precision (AP) and Mean Absolute Error (MAE) (for regression tasks). The results demonstrate the performance of the proposed methods compared to state-of-the-art baselines.
read the caption
Table 1: Results on Long Range Graph Benchmark datasets.
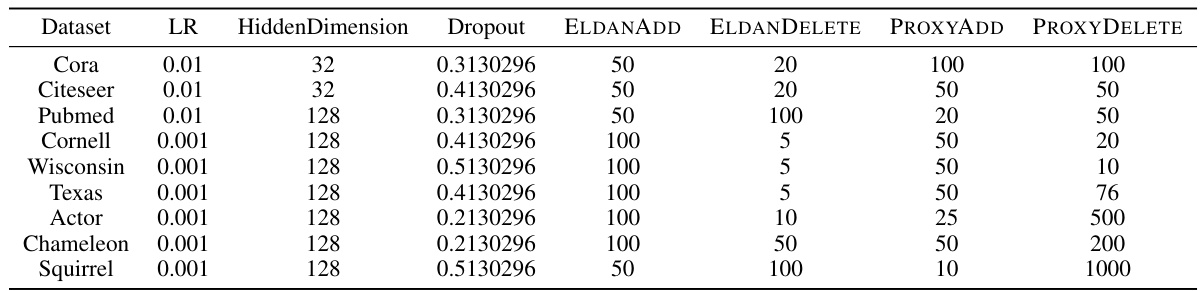
🔼 This table lists the hyperparameters used for the Graph Convolutional Network (GCN) experiments with the proposed edge rewiring algorithms. For each dataset (Cora, Citeseer, Pubmed, Cornell, Wisconsin, Texas, Actor, Chameleon, Squirrel), it specifies the learning rate (LR), hidden dimension size, dropout rate, and the number of edges added or deleted for the ELDANADD, ELDANDELETE, PROXYADD, and PROXYDELETE algorithms.
read the caption
Table 19: Hyperparameters for GCN+our proposed rewiring algorithms.
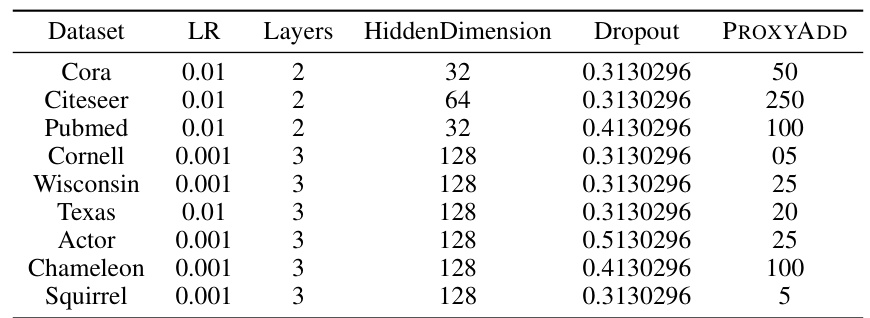
🔼 This table presents the results of node classification experiments using Graph Convolutional Networks (GCNs) enhanced with various graph rewiring techniques. The base GCN model is compared against versions incorporating DIGL, SDRF, FoSR, EldanDELETE, EldanADD, PROXYADD, PROXYDELETE, and RANDOMDELETE methods. The table shows the test accuracy achieved on several benchmark datasets (Cora, Citeseer, Pubmed, Cornell, Wisconsin, Texas, Actor, Chameleon, and Squirrel), highlighting the effectiveness of different rewiring strategies in improving node classification performance. The results reveal how these methods impact accuracy, considering both adding and deleting edges to enhance the spectral gap and manage over-smoothing.
read the caption
Table 10: We compare the performance of GCN augmented with different graph rewiring methods on node classification.

🔼 This table compares the performance of Relational Graph Convolutional Networks (R-GCNs) augmented with three different graph rewiring methods on nine node classification datasets. The methods compared are FoSR (First-order Spectral Rewiring), a method based on Eldan’s criterion (a theoretical guarantee for spectral gap increase), and PROXYADD (a computationally efficient proxy method for spectral gap maximization). The table shows the test accuracy for each method on each dataset, highlighting the effectiveness of the proposed PROXYADD method in several cases.
read the caption
Table 11: Node classification using Relational-GCNs comparing FoSR, Eldan's criterion and PROXYADD.

🔼 This table presents the results of the Long Range Graph Benchmark (LRGB) experiments. The LRGB is designed to specifically test GNN performance in the presence of over-squashing. The table compares the performance of several methods (Baseline-GCN, DRew+GCN, FOSR+GCN, ProxyAdd+GCN, and ProxyDelete+GCN) across three different datasets: PascalVOC-SP, Peptides-Func, and Peptides-Struct, reporting their F1 score (for PascalVOC-SP), Average Precision (AP, for Peptides-Func), and Mean Absolute Error (MAE, for Peptides-Struct). The baseline GCN is a standard Graph Convolutional Network, while the other methods incorporate various graph rewiring techniques to mitigate the effects of over-squashing. The results illustrate the effectiveness of the proposed ProxyAdd and ProxyDelete methods relative to the baseline and other state-of-the-art rewiring methods.
read the caption
Table 1: Results on Long Range Graph Benchmark datasets.

🔼 The table shows the results of different graph rewiring methods on three datasets from the Long Range Graph Benchmark. The methods include a baseline GCN, DRew+GCN, FOSR+GCN, ProxyAdd+GCN, and ProxyDelete+GCN. The metrics reported are Test F1 for PascalVOC-SP, Test AP for Peptides-Func, and Test MAE for Peptides-Struct. The Long Range Graph Benchmark is specifically designed to evaluate graph neural networks’ performance on graphs with long-range dependencies.
read the caption
Table 1: Results on Long Range Graph Benchmark datasets.

🔼 This table lists the hyperparameters used for the DIGL algorithm in the paper’s experiments. It shows the learning rate (LR), dropout rate, hidden dimension size, alpha (α), and kappa (κ) values used for each dataset. These settings were used to tune the DIGL model for node classification experiments.
read the caption
Table 25: Hyperparameters for DIGL.

🔼 This table compares the performance of Graph Convolutional Networks (GCNs) combined with three different graph rewiring methods on graph classification tasks. The methods are: FoSR (First-order Spectral Rewiring), ELDANADD (greedy edge addition based on Eldan’s criterion), and PROXYADD (greedy edge addition based on a proxy for spectral gap changes). The table shows the accuracy achieved by each method on six different benchmark datasets: ENZYMES, MUTAG, IMDB-BINARY, REDDIT-BINARY, COLLAB, and PROTEINS. The results highlight the effectiveness of the proposed methods, especially PROXYADD, in improving graph classification accuracy compared to FoSR.
read the caption
Table 11: Graph classification with GCN comparing FoSR, ELDANADD and PROXYADD.
🔼 This table compares the performance of Graph Convolutional Networks (GCNs) combined with different graph rewiring methods on graph classification tasks. The methods compared are FoSR (First-Order Spectral Rewiring), ELDANADD (Greedy graph addition based on Eldan’s criterion), and PROXYADD (Greedy graph addition using a proxy spectral gap update). The table shows the accuracy achieved by each method on several benchmark datasets including ENZYMES, MUTAG, IMDB-BINARY, REDDIT-BINARY, COLLAB, and PROTEINS. The results illustrate the relative effectiveness of the different rewiring strategies for improving GCN performance on graph classification problems.
read the caption
Table 11: Graph classification with GCN comparing FoSR, ELDANADD and PROXYADD.
Full paper#