↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Bilevel optimization problems are challenging to solve efficiently, especially when constraints are involved. Existing methods often rely on computationally expensive Hessian computations, which limits their applicability to high-dimensional problems. Furthermore, the theoretical understanding of convergence rates for constrained bilevel optimization has been lacking. This paper tackles these issues by focusing on first-order methods that only use first-order derivatives, significantly reducing computational cost. The authors introduce new algorithms for both linear equality and inequality constraints, providing theoretical guarantees on their convergence rates.
The proposed algorithms demonstrate near-optimal convergence for linear equality constraints and dimension-free convergence rates for linear inequality constraints (under an additional assumption). The paper also introduces new nonsmooth, nonconvex optimization methods that can handle inexact information from oracles. The results are supported by numerical experiments, demonstrating their effectiveness. These new algorithms and theoretical analyses significantly advance the state-of-the-art in solving constrained bilevel optimization problems.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in bilevel optimization as it presents the first-order methods for solving linearly constrained bilevel optimization problems. This significantly reduces computational complexity, opening new avenues for applications in diverse fields like meta-learning and hyperparameter optimization. The dimension-free convergence rates achieved under certain assumptions are also a notable contribution, pushing the boundaries of current algorithms.
Visual Insights#
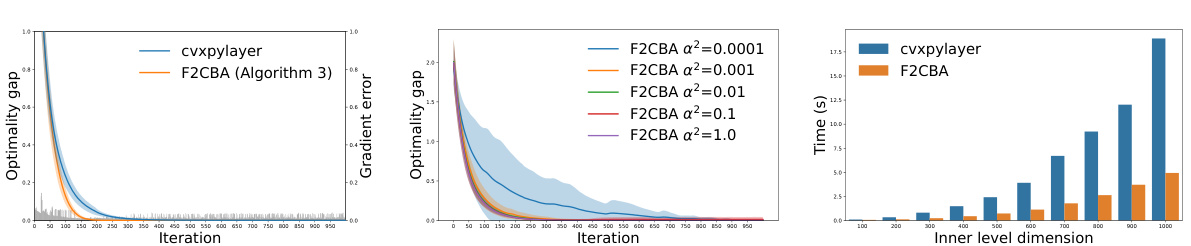
This figure presents a comparison of the performance of Algorithm 3 (F2CBA) with Algorithm 4 for solving a bilevel optimization problem. It shows three subfigures: (a) Convergence and gradient error comparison between F2CBA and cvxpylayer. (b) Convergence analysis with varying levels of gradient inexactness (a) to show the tradeoff between accuracy and speed of convergence. (c) Computation cost per gradient step at various inner level problem dimensions (dy) demonstrating the computational efficiency of F2CBA.

This figure compares the performance of the proposed fully first-order constrained bilevel algorithm (F2CBA) against the cvxpylayer method. Subfigures (a), (b), and (c) show convergence and gradient error, convergence analysis with varying gradient inexactness, and computation cost per gradient step with varying problem sizes, respectively. The experiments were conducted using a toy example (Problem L.1) with specific parameter settings (dx=100, dy=200, const=dy/5, a=0.1).
Full paper#



















