TL;DR#
Predicting the 3D structures of atomic systems is crucial in various scientific domains but remains challenging due to the complexity of atomic interactions and the vastness of the conformational space. Existing generative models often suffer from insufficient exploration of probability paths and persistent hallucinations during sampling, hindering their accuracy.
FlowDPO tackles these challenges by introducing a novel framework that uses flow matching models to explore multiple probability paths. It then employs Direct Preference Optimization (DPO) to refine the model, generating structures that closely align with the ground truth. Theoretical analysis demonstrates the compatibility of DPO with arbitrary Gaussian paths, thereby enhancing the model’s universality. Extensive experiments on antibodies and crystals validate FlowDPO’s superior performance over existing methods, showcasing its potential to advance the field of 3D structure prediction.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces FlowDPO, a novel framework that significantly improves the accuracy of 3D structure prediction. FlowDPO addresses limitations of existing generative models by exploring various probability paths and using Direct Preference Optimization to suppress hallucinations. This advancement has significant implications for drug design, materials science, and other fields reliant on accurate 3D structural modeling. The theoretical contributions provide a strong foundation for future research, opening new avenues for model improvement and enhanced universality.
Visual Insights#
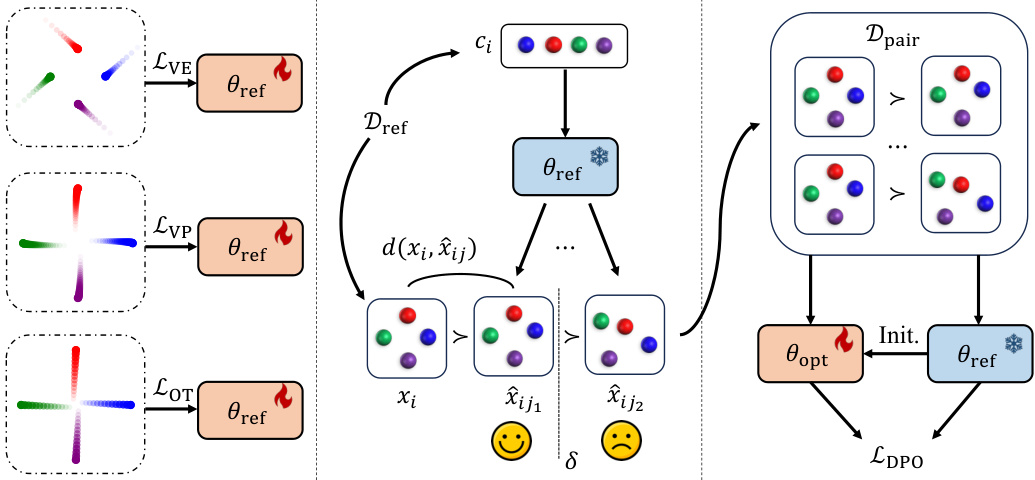
🔼 This figure illustrates the FlowDPO pipeline, showing three stages: (a) training flow models with different Gaussian paths (VE, VP, OT), (b) constructing a preference dataset by comparing generated structures with ground truth, and (c) direct preference optimization to refine the model. The model uses context (Ci) and pre-trained flow models (θref) to generate multiple candidates (xij) for each ground truth structure (xi). The distance between generated and ground truth structures determines the preference dataset (Dpair), used to fine-tune the model (θopt) via direct preference optimization (LDPO).
read the caption
Figure 1: Overview of the proposed FlowDPO pipeline. As described in Section 3.1, the process begins by training a flow matching model, denoted as θref, using an arbitrary pre-defined Gaussian path. Next, as outlined in Section 3.2, we construct a preference dataset, Dpair, by evaluating the distances between generated samples xij and the ground structure xi under a given context condition Ci—such as an antibody sequence or crystal composition. These samples are derived from the reference training set Dref. This dataset is then used to fine-tune the model θopt through the DPO training objective LDPO, detailed in Section 3.3.

🔼 This table lists the parameters for three different Gaussian paths used in the FlowDPO model for geometric graph flow matching. These paths determine how samples are transformed from a prior distribution to the target data distribution, influencing the model’s ability to generate diverse and accurate structures. The table provides the mean and standard deviation for each path, as well as the corresponding conditional vector field. These parameters are crucial for understanding the behavior and flexibility of the FlowDPO approach.
read the caption
Table 1: Parameters of different Gaussian paths. VE, VP and OT represent Variable Exploding, Variable Preserving and Optimal Transport, respectively.
In-depth insights#
Flow Matching Models#
Flow matching models offer a powerful paradigm for generative modeling by learning a continuous transformation, or flow, between a simple prior distribution and a complex target distribution. Instead of relying on discrete steps like diffusion models, they learn a continuous vector field that guides samples from the prior towards the target. This approach offers greater flexibility in exploring probability paths and potentially generating more diverse and realistic samples, avoiding the limitations of diffusion models which often suffer from mode collapse or hallucination. The choice of the flow and the prior distribution influence the model’s expressivity and efficiency. The theoretical properties of flow matching models are still under active research, but they show promise for surpassing the limitations of earlier generative approaches in various applications, including 3D structure prediction where the intricacy of the conformational space necessitates efficient exploration of probability space.
DPO Optimization#
Direct Preference Optimization (DPO) presents a novel approach to enhance generative models by directly aligning them with desired preferences, overcoming limitations of traditional likelihood-based training. Instead of maximizing the probability of generating ground truth structures, DPO leverages a preference dataset comprising pairs of samples, explicitly indicating which is preferred. This allows the model to learn the underlying preference distribution, leading to improved generation quality and reduced hallucinations. The theoretical analysis demonstrates compatibility with various Gaussian paths, broadening the applicability of the method beyond diffusion models. The incorporation of DPO within the FlowDPO framework significantly improves the accuracy of generated 3D structures for antibodies and crystals, showcasing its effectiveness in structure prediction.
Antibody Structure#
Antibody structure prediction is a critical area of research with significant implications for drug design and development. Accurate modeling of antibody structures, particularly the highly variable complementarity-determining regions (CDRs), remains a challenge due to the vastness of the conformational space and complex interactions between the antibody and its target antigen. The paper explores methods that leverage generative models to tackle this, utilizing flow-based approaches to explore diverse probability paths for structure generation. The incorporation of Direct Preference Optimization (DPO) is particularly noteworthy, aiming to guide the model towards generating structures more closely aligned with experimental data and suppressing the formation of unrealistic (hallucinated) structures. This approach demonstrates the potential to enhance both the accuracy and reliability of predicted antibody structures, which in turn could lead to improved antibody design and drug discovery processes. The theoretical analysis presented, showing compatibility of DPO with various Gaussian paths, adds to the robustness of the proposed method. The experimental results on antibody datasets showcase significant improvements in prediction accuracy compared to previous methods. However, limitations remain, primarily concerning the generalizability beyond Gaussian paths and the need for further validation through wet-lab experiments.
Crystal Prediction#
Predicting crystal structures is crucial in materials science, and this paper explores using flow-based models and Direct Preference Optimization (DPO) to enhance prediction accuracy. The approach leverages the power of flow matching models to explore multiple probability paths, generating diverse candidate crystal structures. A key strength is the theoretical justification for DPO’s compatibility with arbitrary Gaussian paths, ensuring broader applicability. The generated structures are then compared to ground truth, automatically creating a preference dataset to fine-tune the model. This iterative process, combining diverse structure generation with DPO-based refinement, aims to reduce hallucinations and improve alignment with the desired distribution. Experiments on diverse crystal datasets show substantial improvements over existing methods, highlighting FlowDPO’s efficacy in predicting complex crystal structures from compositions alone. The method’s success in incorporating varied probability paths and its theoretical foundation points to a significant advancement in the field of crystal structure prediction.
Future Directions#
Future research could explore extending FlowDPO’s theoretical framework beyond Gaussian paths, enhancing its applicability to diverse probability distributions. Investigating alternative objective functions for DPO, potentially incorporating concepts from reinforcement learning, may further improve the model’s alignment with desired properties. A crucial area for future work is validation through extensive wet-lab experiments, bridging the gap between computational predictions and experimental observations. This would involve testing the accuracy of FlowDPO-generated structures in real-world scenarios, building confidence in its practical utility. Furthermore, exploring different types of flow matching models and their compatibility with DPO could lead to significant performance gains and increased robustness. Finally, scaling FlowDPO to handle larger and more complex atomic systems presents a considerable challenge but also offers a pathway towards more impactful applications in materials science and drug discovery.
More visual insights#
More on figures
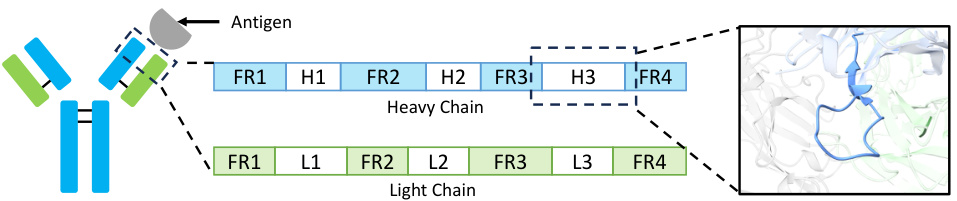
🔼 This figure shows a schematic of an antibody’s structure, highlighting the variable domains, which are composed of heavy and light chains. Each chain contains four framework regions (FRs) and three complementarity-determining regions (CDRs), which are involved in antigen binding. The CDRs, particularly CDR-H3, are highly variable and are the key regions that determine the antibody’s specificity. The image also shows a 3D representation of an antibody.
read the caption
Figure 2: Graphical depiction of antibody variable domains, which consist of a heavy chain and a light chain. Each chain is equipped with 4 Framework Regions (FRs) and 3 Complementarity-Determining Regions (CDRs). The CDRs, especially CDR-H3, are volatile and thus are the key focus.
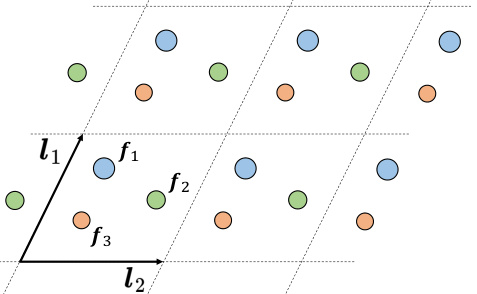
🔼 This figure illustrates the fundamental concept of a crystal structure. Crystals are characterized by the periodic repetition of a unit cell in three-dimensional space. The unit cell is the smallest repeating structural unit that contains the complete pattern of the crystal structure. The figure visually shows a unit cell with different colored atoms, representing different elements, arranged in a specific pattern. The dashed lines indicate the boundaries of the unit cells, which extend infinitely in all three dimensions. This periodic arrangement is a key feature that differentiates crystals from other materials.
read the caption
Figure 3: A crystal is the infinite periodic arrangement of atoms, and the repeating unit is named as a unit cell.
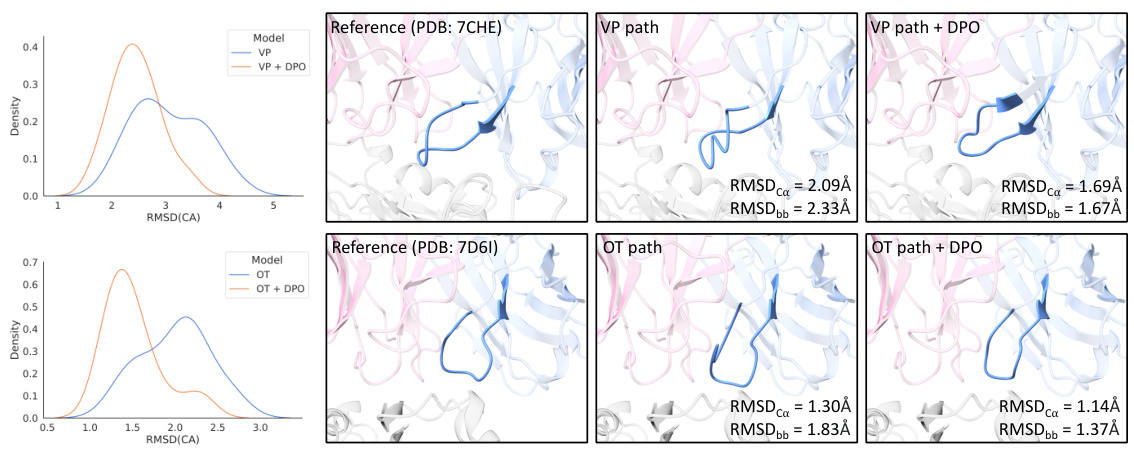
🔼 This figure shows examples of generated CDR-H3 structures and their RMSD distributions for different probability paths (VP and OT) with and without DPO. The left column displays the RMSD distributions for VP and OT paths, both before and after applying DPO. The right columns show 3D structures of generated CDR-H3 and reference structure for two examples, highlighting how DPO refines structure quality and corrects physical inconsistencies (like twisted backbones). DPO is shown to shift the distributions towards lower RMSD values and eliminate the second peak representing lower-quality conformations.
read the caption
Figure 4: Examples of generated CDR-H3 structures and the distribution of RMSDCA for different antigen-antibody complexes and different probability paths. The visualized samples are the ones with the lowest RMSD of all the generated counterparts for the corresponding complexes. In addition to driving the distribution towards lower RMSD, it is also observed that the DPO phase tends to rectify the physical invalidity (e.g., twisted backbone in the above examples) in the generated samples.
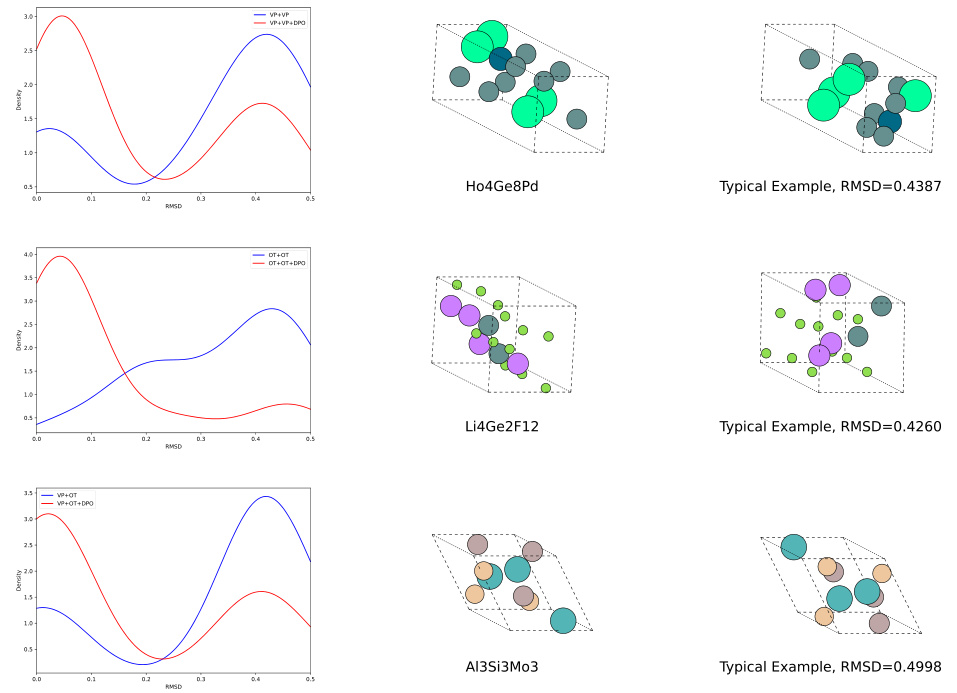
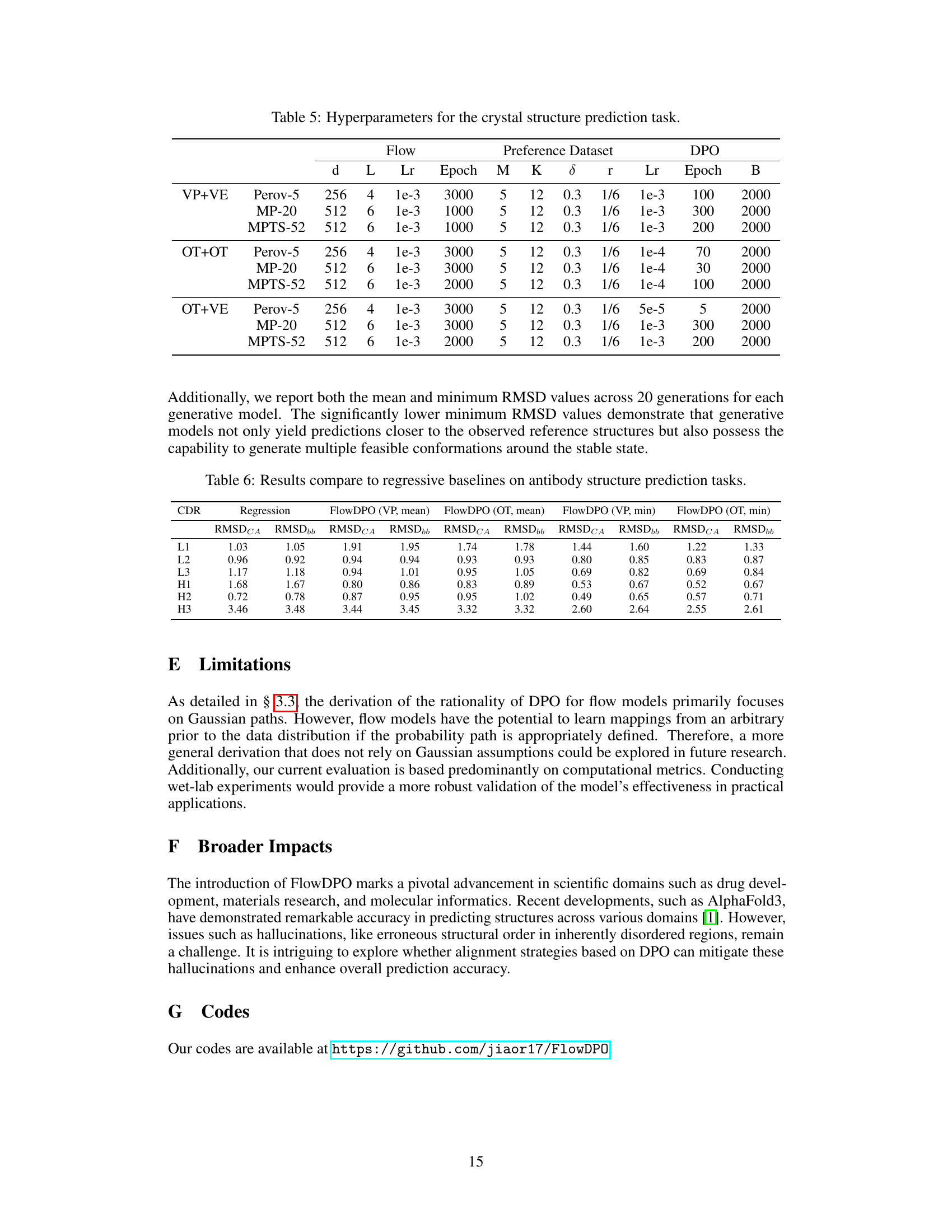
🔼 This figure shows the results of crystal structure prediction. The left column displays the distribution of RMSD (Root Mean Square Deviation) values for models before and after applying Direct Preference Optimization (DPO). The middle column presents the ground truth crystal structures, while the right column highlights examples of structures generated with high RMSD values, indicating poorer predictions that were improved by the DPO process. The visualization demonstrates the effectiveness of DPO in improving the accuracy of the generated crystal structures by reducing the number of low-quality predictions.
read the caption
Figure 5: Visualizations on crystal structure prediction results. The left column depicts the RMSD distribution of the models before (blue) and after (red) DPO. The middle column shows the ground truth structures, and the right column shows typical high RMSD generations to be suppressed.
More on tables

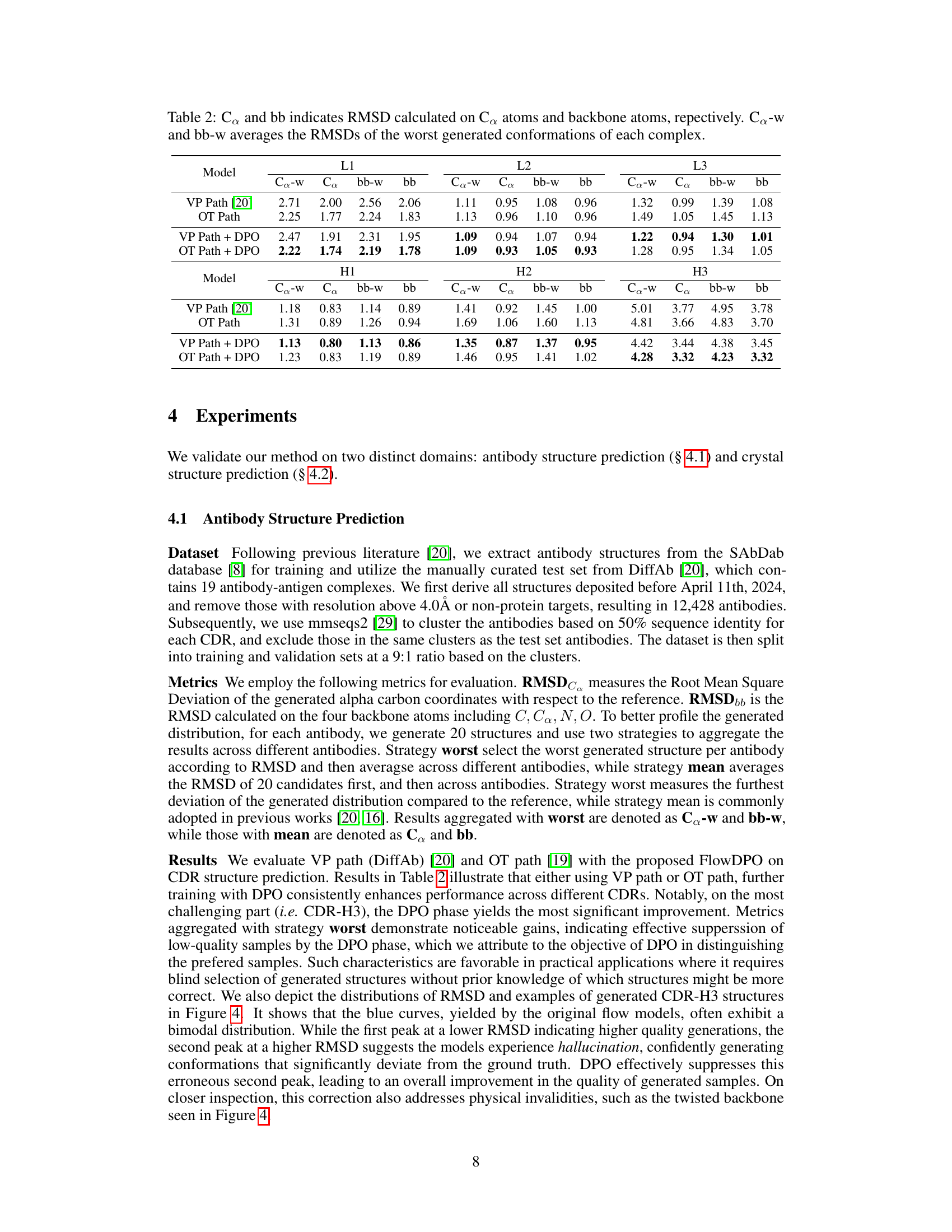
🔼 This table presents the results of antibody structure prediction using different methods (VP Path, OT Path, VP Path + DPO, OT Path + DPO). For each method and each CDR region (L1, L2, L3, H1, H2, H3), it shows the Root Mean Square Deviation (RMSD) calculated using two metrics: RMSD on alpha-carbon atoms (Ca) and RMSD on backbone atoms (bb). It also provides the average RMSD of the worst-performing generated structures for each antibody (Ca-w and bb-w) to highlight the robustness of each method.
read the caption
Table 2: Co and bb indicates RMSD calculated on Co atoms and backbone atoms, repectively. Ca-w and bb-w averages the RMSDs of the worst generated conformations of each complex.
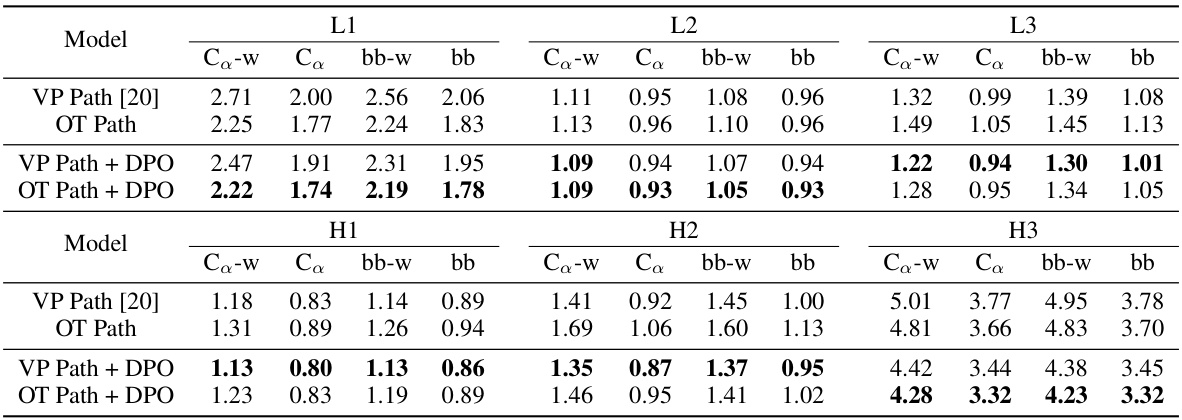
🔼 This table presents the results of antibody structure prediction using different methods (VP Path, OT Path, VP Path + DPO, OT Path + DPO). For each method, it shows the Root Mean Square Deviation (RMSD) calculated using two different metrics: one based on the alpha-carbon atoms (Ca) and one based on the backbone atoms (bb). It also shows the average RMSD for the worst generated conformations of each antibody-antigen complex (Ca-w and bb-w). The results are broken down by CDR (Complementarity-Determining Region) for easier comparison between different methods and CDRs.
read the caption
Table 2: Co and bb indicates RMSD calculated on Co atoms and backbone atoms, repectively. Ca-w and bb-w averages the RMSDs of the worst generated conformations of each complex.
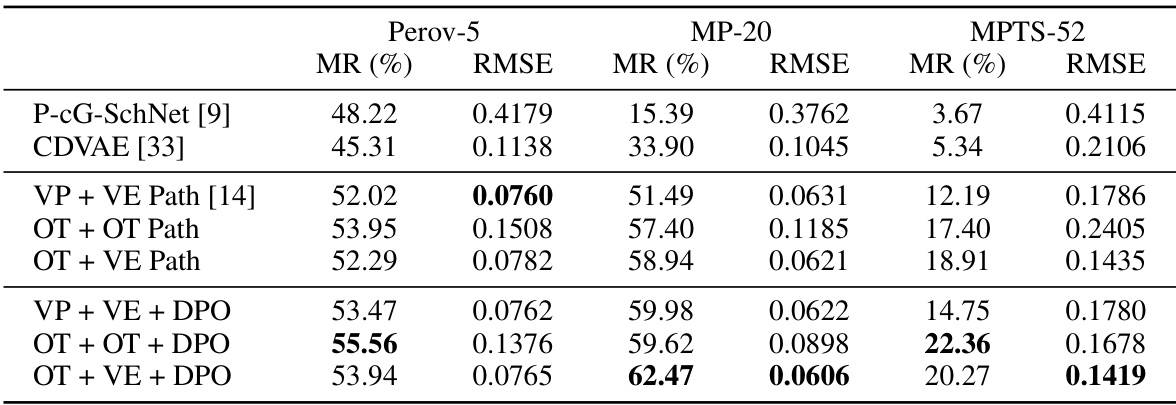
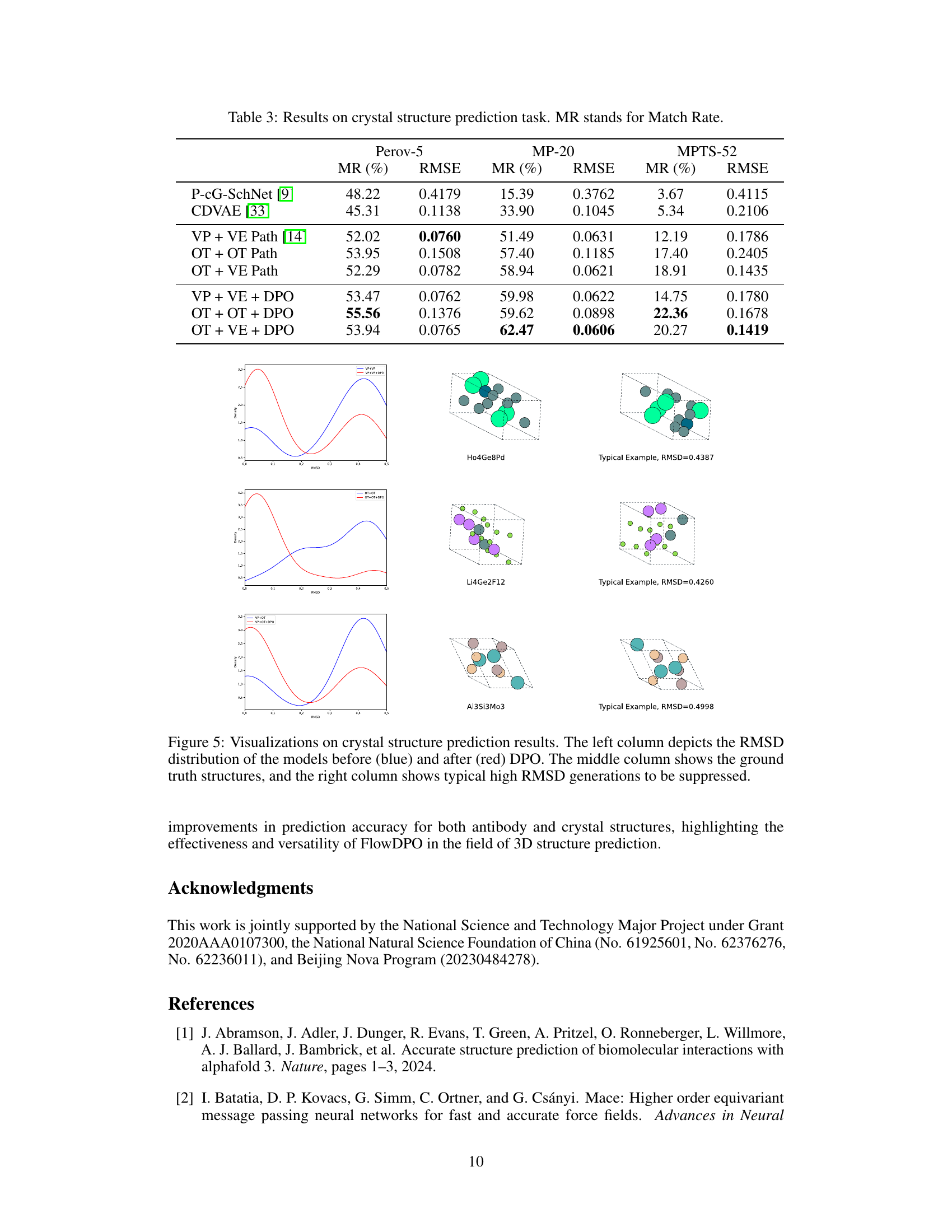
🔼 This table presents the results of crystal structure prediction experiments on three datasets (Perov-5, MP-20, MPTS-52) using different methods. The methods include two baseline methods (P-cG-SchNet and CDVAE), three flow path methods (VP + VE, OT + OT, OT + VE), and three flow path methods further enhanced by Direct Preference Optimization (DPO). For each method and dataset, the Match Rate (MR) and Root Mean Square Deviation (RMSE) are reported. The MR indicates the percentage of correctly predicted crystal structures, while the RMSE measures the average structural difference between the predicted and true structures. Lower RMSE values indicate better prediction accuracy. The table highlights the performance improvements achieved by incorporating DPO into the flow path methods.
read the caption
Table 3: Results on crystal structure prediction task. MR stands for Match Rate.
🔼 This table lists the hyperparameters used in the antibody structure prediction experiments. It shows the settings for different flow models (VP and OT paths), the preference dataset construction (M, K, δ, r), and the direct preference optimization (DPO) training (Lr, Epoch, β). Each row represents a different CDR (Complementarity-Determining Region) within the antibody structure, indicating the specific hyperparameter settings used for each CDR’s prediction task.
read the caption
Table 4: Hyperparameters for the antibody structure prediction task.
🔼 This table lists the hyperparameters used in the crystal structure prediction experiments. For each of three different combinations of probability paths (VP+VE, OT+OT, OT+VE), it shows the hyperparameters for the flow model, preference dataset construction, and direct preference optimization (DPO). These hyperparameters include parameters related to the model architecture, training process, preference dataset creation (number of candidates, preference threshold, etc.) and the DPO optimization itself (learning rate, number of epochs, beta parameter). The table is organized by path type and dataset (Perov-5, MP-20, MPTS-52) for clarity.
read the caption
Table 5: Hyperparameters for the crystal structure prediction task.

🔼 This table presents the results of antibody structure prediction using different methods (VP Path, OT Path, VP Path + DPO, OT Path + DPO). For each method, the Root Mean Square Deviation (RMSD) is calculated for Cα atoms (Ca) and backbone atoms (bb), both considering the average RMSD across all generated structures (mean) and the worst-performing structure (worst). The results are broken down by CDR region (L1, L2, L3, H1, H2, H3). Lower RMSD values indicate better prediction accuracy.
read the caption
Table 2: Co and bb indicates RMSD calculated on Co atoms and backbone atoms, repectively. Ca-w and bb-w averages the RMSDs of the worst generated conformations of each complex.
Full paper#