TL;DR#
Data reduction is critical for analyzing massive datasets, but effective techniques are lacking for Poisson regression models, especially when using identity or square-root link functions. Existing methods often lack theoretical guarantees or suffer from limitations in scalability. This is a significant hurdle for researchers needing to work with large-scale count data.
This research introduces novel data subsampling techniques for Poisson regression using the pth-root link function. The key is a novel complexity parameter and a domain-shifting approach. The authors prove the existence of sublinear coresets with strong approximation guarantees when the complexity parameter is small, significantly improving data reduction for Poisson regression. Tight bounds on the size of the required coreset are established, demonstrating the effectiveness of their method.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on large datasets and seeking efficient data reduction techniques for Poisson regression. It introduces a novel framework that provides rigorous theoretical guarantees, paving the way for more efficient and reliable statistical modeling.
Visual Insights#
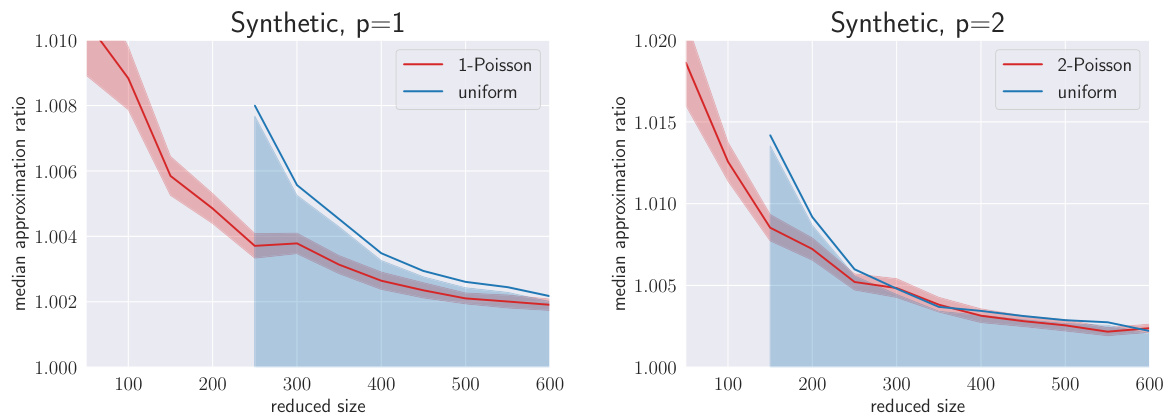
🔼 The figure shows the results of an experiment comparing the performance of the proposed coreset construction method against uniform sampling for Poisson regression with ID-link and square root-link. The y-axis represents the median approximation ratio, while the x-axis shows the reduced size of the dataset. The plots visualize the median approximation ratio and its standard error for both methods across various reduced dataset sizes. Notably, the uniform sampling method frequently produces infeasible results for smaller dataset sizes, while the proposed method consistently yields valid approximations.
read the caption
Figure 1: Experimental results for two synthetic data sets with p = 1 (left), respectively p = 2 (right). Our method is presented in red and compared against uniform sampling, which is presented in blue. Solid lines indicate the median and shaded areas indicate ±2 standard errors around the median taken across 201 independent repetitions for each reduced size between 50 and 600 in equal increment steps of 50. For the blue shaded area below the blue solid line, only feasible repetitions were counted, while the blue shaded area above represents the unbounded standard error without this restriction. For some lower reduced sizes, even the median was infinite, which results in an interrupted blue solid line. This indicates that more than half of the repetitions gave infeasible results when using uniform sampling with low sample sizes, while our method never produced infeasible results.

🔼 This figure compares the performance of the proposed Poisson subsampling method against uniform sampling for two synthetic datasets, one with p=1 and the other with p=2. The median approximation ratio is plotted against the reduced dataset size, with error bars representing 2 times the standard error. The results show that the proposed method consistently outperforms uniform sampling, particularly for smaller reduced dataset sizes where uniform sampling produces many infeasible results.
read the caption
Figure 1: Experimental results for two synthetic data sets with p = 1 (left), respectively p = 2 (right). Our method is presented in red and compared against uniform sampling, which is presented in blue. Solid lines indicate the median and shaded areas indicate ±2 standard errors around the median taken across 201 independent repetitions for each reduced size between 50 and 600 in equal increment steps of 50. For the blue shaded area below the blue solid line, only feasible repetitions were counted, while the blue shaded area above represents the unbounded standard error without this restriction. For some lower reduced sizes, even the median was infinite, which results in an interrupted blue solid line. This indicates that more than half of the repetitions gave infeasible results when using uniform sampling with low sample sizes, while our method never produced infeasible results.
Full paper#



















