TL;DR#
Current diffusion models often suffer from generating data that reflects biases present in the training dataset. This limitation restricts their use in various applications requiring controlled data generation, such as those with fairness or pre-trained model distribution requirements. This necessitates the development of constrained diffusion models that can effectively address the distribution bias.
This research introduces a novel framework for training constrained diffusion models. The training process is presented as a constrained distribution optimization problem. This problem aims to minimize the difference between the original and generated data distributions while adhering to the specified constraints on the generated data distribution. A dual training algorithm is proposed for model training and the optimality of this algorithm is also analyzed. Experiments demonstrate successful application in fair sampling and model adaptation tasks, highlighting the effectiveness of the approach.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on generative models, particularly diffusion models. It addresses the critical issue of bias and limitations in current diffusion models by introducing a novel constrained optimization framework. This framework enables generating data that satisfies specific requirements, such as fairness or adherence to pre-trained model distributions. The proposed dual training algorithm offers a practical method for implementing constraints. The results demonstrate significant improvements in fairness and model adaptation, opening exciting new avenues for future research in various domains that require data generation under constraints. The provided analysis strengthens theoretical understanding and enhances the applicability of diffusion models.
Visual Insights#
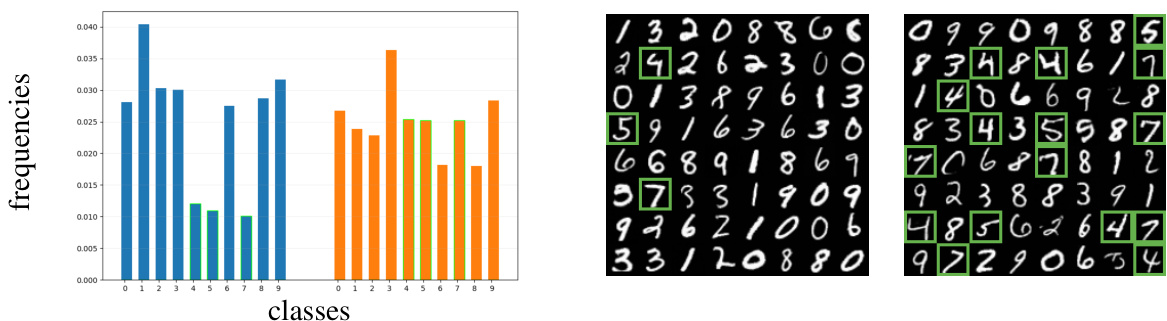
🔼 This figure compares the performance of constrained and unconstrained diffusion models trained on the MNIST dataset, focusing on three under-represented digits (4, 5, and 7). The left panel shows the frequency distribution of generated digits for both model types, highlighting the improved balance achieved by the constrained model. The middle and right panels display example digit generations from the unconstrained and constrained models, respectively. The FID (Fréchet Inception Distance) scores are provided as quantitative measures of the image quality, indicating that the constrained model produces higher-quality images.
read the caption
Figure 1: Generation performance comparison of constrained and unconstrained models that are trained on MNIST with three minorities: 4, 5, 7. (Left) Frequencies of ten digits that are generated by an unconstrained model () and our constrained model (); (Middle) Generated digits from unconstrained model (FID 15.9); (Right) Generated digits from our constrained model (FID 13.4).

🔼 This table lists the hyperparameters of the U-Net model used as the noise predictor in the diffusion model. It specifies the number of ResNet layers per U-Net block, the number of ResNet down/upsampling blocks, and the number of output channels for each U-Net block.
read the caption
Table 1: Parameters of U-net Model used as noise predictor
In-depth insights#
Dual Training#
The concept of ‘Dual Training’ in the context of constrained diffusion models is a novel approach to address the challenge of generating data while adhering to specific requirements. It leverages the power of constrained optimization by framing the problem as a balance between optimizing a primary objective (e.g., minimizing reconstruction error) and satisfying constraints (e.g., ensuring fair representation of underrepresented classes). The proposed ‘dual training’ method involves a Lagrangian-based formulation that elegantly combines these objectives, where the Lagrangian multipliers act as weights to balance the importance of the objective and constraints. The core insight lies in leveraging strong duality, enabling a transformation of the constrained optimization problem into an equivalent unconstrained one in the dual space. This significantly simplifies the training process by making it less computationally expensive than directly dealing with the original constrained problem. Moreover, the authors demonstrate convergence and optimality results that offer theoretical guarantees on the generated data’s alignment with both the primary objective and the constraints. Finally, empirical evaluations showcase the effectiveness of this framework in two key areas: ensuring fairness in data generation and adapting pre-trained models to new datasets. The emphasis on dual space optimization and the resultant theoretical underpinnings constitute a significant contribution to constrained generative modeling.
KL Divergence#
The concept of Kullback-Leibler (KL) divergence is central to the paper, forming the foundation for the proposed constrained diffusion models. KL divergence quantifies the difference between two probability distributions, acting as a measure of how much one distribution deviates from another. In this context, it’s used to formalize a constrained optimization problem during model training. The authors leverage KL divergence to minimize the difference between the original data distribution and the distribution generated by the diffusion model, while simultaneously ensuring that the generated data adheres to specific constraints expressed via additional desired distributions. The constraints are formulated as bounds on KL divergences between the model and these target distributions. This elegant framing allows the model to balance the objective of accurately representing the original data with the requirement of satisfying pre-defined constraints, leading to a more controlled and potentially fairer or more specific data generation process. The use of KL divergence in the infinite-dimensional distribution space and its analysis via strong duality are key theoretical contributions of this work.
Fair Sampling#
The concept of “Fair Sampling” in the context of generative models, particularly diffusion models, addresses the issue of bias amplification. Standard training procedures can lead to models that disproportionately generate samples from over-represented classes in the training data, thus perpetuating or even exacerbating existing societal biases. Fair sampling techniques aim to mitigate this bias by ensuring a more equitable representation of all classes in the generated data. This might involve modifying the training process, such as re-weighting samples or applying constraints during optimization, to encourage the model to learn a fairer underlying distribution. Achieving fair sampling is not merely about equal representation, however; it’s about addressing underlying biases that might lead to unfair outcomes even with seemingly balanced outputs. The success of such methods depends on the specific constraints chosen and how effectively they’re incorporated into the model’s learning process. The evaluation of fair sampling often involves measuring the distribution of generated samples across different classes and comparing it to a fair baseline, thereby quantifying the model’s fairness.
Model Adaptation#
Model adaptation in the context of diffusion models focuses on efficiently transferring a pre-trained model’s knowledge to a new dataset. This is crucial because training diffusion models from scratch is computationally expensive. Effective adaptation strategies must balance leveraging the pre-trained model’s strengths with avoiding catastrophic forgetting or overfitting to the new data. Several approaches exist, including fine-tuning, where model parameters are adjusted based on the new data’s characteristics; and other methods that impose constraints, ensuring the adapted model remains close to the original distribution while adequately representing the new dataset. Constrained optimization frameworks are particularly promising, offering a principled way to manage the trade-off between fidelity to the original model and performance on the new data. The choice of constraints is critical and will depend on the specific requirements of the adaptation task; for example, in fair data generation, constraints might ensure equitable representation of underrepresented groups. Careful consideration of the optimization process, including the selection of hyperparameters and evaluation metrics, is crucial to ensure successful and robust model adaptation. Success in model adaptation ultimately depends on achieving a balance between retaining the desirable properties of the pre-trained model and accurately capturing the characteristics of the target distribution.
Future Works#
The paper’s ‘Future Works’ section could explore several promising avenues. Extending the framework to handle more diverse constraints beyond KL-divergence, such as those involving specific image features or semantic properties, would significantly broaden its applicability. Investigating alternative training methodologies that might improve convergence speed or efficiency, potentially incorporating techniques like meta-learning or reinforcement learning, is also crucial. A more in-depth analysis of the impact of different hyperparameter settings, particularly the effects of relaxation cost and dual variable update schemes, could provide greater insight into optimal model training strategies. Furthermore, applying the constrained diffusion model to a wider range of datasets and generation tasks, including video, audio, or 3D models, is important for demonstrating its generalizability and practical value. Finally, developing robust methods for quantifying the trade-off between objective function performance and constraint satisfaction would be beneficial for evaluating the overall effectiveness of the model.
More visual insights#
More on figures

🔼 This figure compares the performance of constrained and unconstrained diffusion models trained on the Celeb-A dataset, which has an underrepresentation of male faces. The left panel shows the frequency of male and female faces generated by both models. The middle and right panels display sample images generated by the unconstrained and constrained models, respectively, along with their FID scores (Frechet Inception Distance). The constrained model shows improved generation of male faces, indicating that the constraints successfully mitigated the bias towards female faces in the original dataset.
read the caption
Figure 2: Generation performance comparison of constrained and unconstrained models that are trained on Celeb-A with male minority. (Left) Frequencies of two genders that are generated by an unconstrained model () and our constrained model (); (Middle) Generated faces from unconstrained model (FID 19.6); (Right) Generated faces from our constrained model (FID 11.6).

🔼 This figure compares the performance of constrained and unconstrained diffusion models trained on the MNIST dataset. The MNIST dataset has been modified to create an imbalance, with digits 4, 5, and 7 under-represented. The left panel shows the frequency of each digit generated by both the constrained and unconstrained models, illustrating that the constrained model generates a more balanced distribution of digits. The middle and right panels show example generated images from the unconstrained and constrained models, respectively, with their associated FID (Fréchet Inception Distance) scores. A lower FID score indicates better image quality and a closer match to real MNIST images.
read the caption
Figure 1: Generation performance comparison of constrained and unconstrained models that are trained on MNIST with three minorities: 4, 5, 7. (Left) Frequencies of ten digits that are generated by an unconstrained model () and our constrained model (); (Middle) Generated digits from unconstrained model (FID 15.9); (Right) Generated digits from our constrained model (FID 13.4).

🔼 This figure compares the performance of constrained and unconstrained diffusion models trained on the MNIST dataset, focusing on three underrepresented digits (4, 5, and 7). The left panel shows the frequency distribution of generated digits for both models. The middle and right panels display sample images generated by the unconstrained and constrained models, respectively. The Fréchet Inception Distance (FID) scores are provided, indicating that the constrained model achieves a lower FID score (13.4) than the unconstrained model (15.9), suggesting improved generation quality.
read the caption
Figure 1: Generation performance comparison of constrained and unconstrained models that are trained on MNIST with three minorities: 4, 5, 7. (Left) Frequencies of ten digits that are generated by an unconstrained model () and our constrained model (); (Middle) Generated digits from unconstrained model (FID 15.9); (Right) Generated digits from our constrained model (FID 13.4).
More on tables
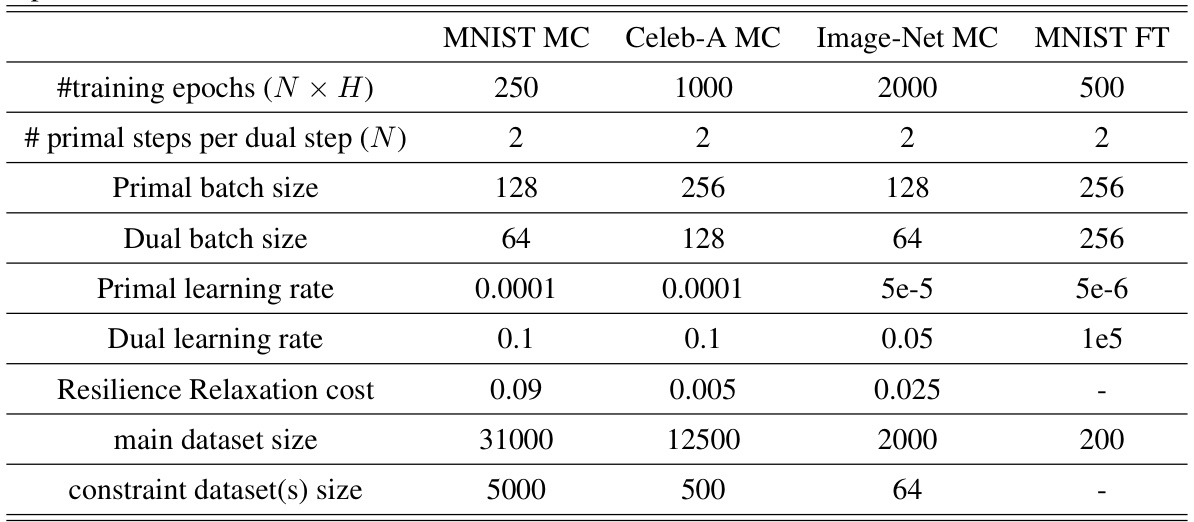
🔼 This table lists the hyperparameter settings used in the main experiments of the paper. It includes details for Minority Class (MC) and Fine-Tuning (FT) experiments on MNIST, CelebA, and ImageNet datasets. The hyperparameters shown are: the number of training epochs, the number of primal steps per dual step, primal and dual batch sizes, primal and dual learning rates, resilience relaxation cost, the size of the main dataset, and the size of the constraint dataset(s). The ‘-’ indicates that resilience was not used in that particular experiment.
read the caption
Table 2: Hyperparameter values used in the main experiments. MC denotes Minority Class experiments and FT denotes Fine-Tuning experiments. - denotes that resilience was not used for the experiment.

🔼 This table shows the FID scores achieved by the constrained diffusion model trained on MNIST dataset using different combinations of primal and dual batch sizes. The results illustrate the impact of varying these batch size parameters on the model’s performance, as measured by the FID score.
read the caption
Table 3: Constrained model trained on MNIST with different Primal/Dual Batch sizes
Full paper#



















