Only Strict Saddles in the Energy Landscape of Predictive Coding Networks?

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it offers a novel perspective on the optimization challenges in predictive coding networks (PCNs). By revealing the impact of PC inference on the loss landscape, it addresses a critical gap in our theoretical understanding of PCNs, paving the way for more efficient and robust training algorithms. Its findings are relevant to researchers exploring energy-based models, and the methods introduced can inspire further studies on improving the efficiency and scaling of PCNs.

Visual Insights

#

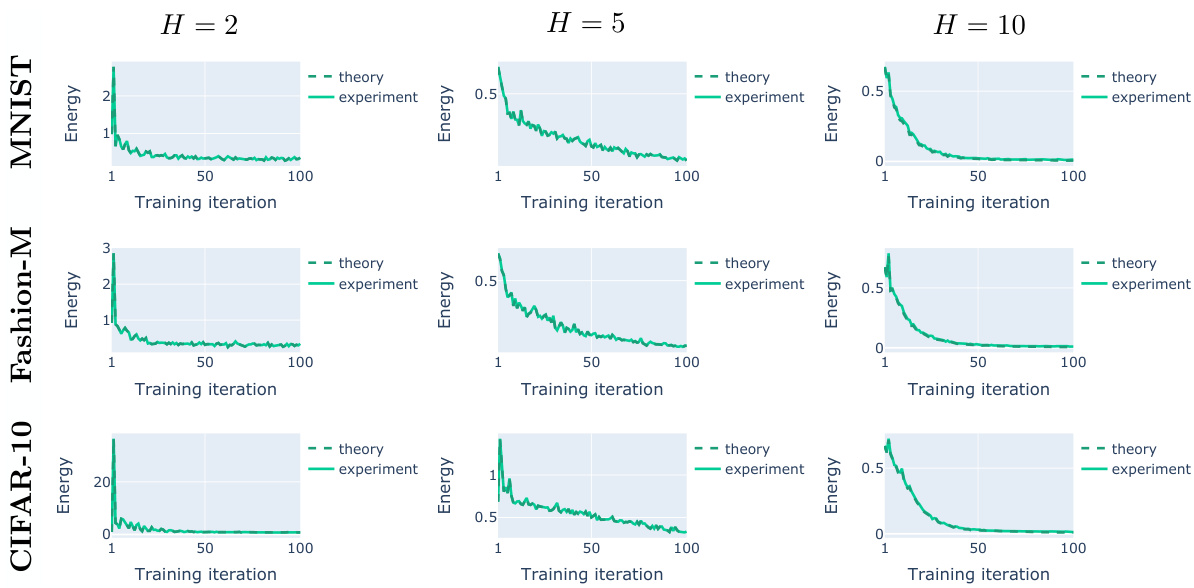
This figure empirically validates Theorem 1, which provides a closed-form solution for the equilibrated energy of deep linear networks (DLNs). The plot shows the energy at inference equilibrium (where ∂F/∂z ≈ 0) for DLNs trained on three different datasets (MNIST, Fashion-MNIST, and CIFAR-10) and with three different numbers of hidden layers (H=2, 5, and 10). The experimental results closely match the theoretical predictions, demonstrating the accuracy of the derived formula for the equilibrated energy.

In-depth insights

#

PC Energy Geometry

#

The concept of ‘PC Energy Geometry’ refers to the shape of the energy landscape in predictive coding (PC) networks. Understanding this geometry is crucial because it dictates how easily the network learns, especially concerning the presence and nature of saddle points—regions where the gradient vanishes but the curvature isn’t strictly positive or negative. The paper investigates how PC’s iterative inference process alters this landscape, transforming many non-strict saddles (difficult to escape) into strict ones (easier to escape). This implies that PC might alleviate some of the challenges associated with the optimization of deep neural networks, such as vanishing gradients. The analysis uses deep linear networks for theoretical tractability and generalizes the findings empirically to non-linear networks. The key contribution lies in connecting the geometry of PC’s energy landscape to the improved optimization of the network. The study reveals a fundamental relationship between the iterative inference procedure and the benign nature of the energy landscape during PC training.

Strict Saddle Escape

#

The concept of “Strict Saddle Escape” in the context of optimization algorithms for neural networks is crucial. Strict saddles, unlike non-strict saddles, possess a negative curvature in at least one direction, making them more challenging for gradient-based methods. The research likely explores how various optimization techniques, particularly predictive coding (PC), approach and overcome these strict saddles. The findings might demonstrate that PC’s iterative inference process alters the loss landscape, making the strict saddles easier to escape. This could offer a valuable advantage over traditional backpropagation methods by accelerating convergence and enhancing robustness. A key aspect could be how PC’s inference transforms the landscape’s geometry, potentially by rescaling the loss function or modifying its curvature near the strict saddles. The theoretical analysis and experimental results would aim to verify this behavior, and might provide practical implications for training deeper and more complex neural networks.

DLN Equilibration

#

The concept of “DLN Equilibration” centers on the equilibrium state reached by Deep Linear Networks (DLNs) during predictive coding (PC) inference. This equilibrium, a key aspect of PC, precedes weight updates, offering a unique learning dynamic. The paper investigates the geometry of the loss landscape at this equilibrium point, demonstrating that the equilibrated energy is a rescaled mean squared error (MSE) loss. This rescaling, dependent on network weights, is a crucial finding, revealing how PC fundamentally alters the learning landscape. The authors show that many non-strict saddles in the original MSE loss transform into strict saddles in the equilibrated energy, improving optimization robustness. This transformation, particularly affecting rank-zero saddles including the origin, makes the loss landscape more amenable to gradient descent. The theory is comprehensively validated through experiments on both linear and nonlinear networks. The conjecture that all saddles become strict in the equilibrated energy landscape highlights a key benefit of PC inference, potentially addressing the vanishing gradient problem while also explaining the challenges in scaling PC to larger, deeper networks.

Non-linear Tests

#

In exploring the energy landscape of predictive coding (PC) networks, the inclusion of non-linear tests is crucial for validating the theoretical findings derived from deep linear networks (DLNs). DLNs, while useful for initial theoretical analysis, do not fully capture the complexities of real-world neural networks. Non-linear tests using common activation functions (e.g., ReLU, tanh) and convolutional architectures are essential to determine if the theoretical observations about strict saddles in the equilibrated energy landscape generalize beyond the simplified linear setting. Successful extension to non-linear networks would strengthen the claim that PC inference fundamentally alters the loss landscape, making it more robust and less susceptible to vanishing gradients, a significant challenge in training deep networks. The empirical results from these non-linear tests should show faster convergence and escape from saddles for PC compared to backpropagation (BP), supporting the central hypothesis of the paper. However, negative results might point towards the existence of non-strict saddles in non-linear PC networks, indicating the limitations of the theory and highlighting avenues for future research. Discrepancies between linear and non-linear results could help refine our understanding of the underlying mechanisms by which PC inference improves optimization.

PC Scalability

#

Predictive coding (PC) shows promise in addressing challenges associated with backpropagation, but its scalability remains a significant hurdle. The inference process, crucial to PC, incurs substantial computational cost, which amplifies with network depth. While PC offers potential advantages in escaping saddle points and mitigating vanishing gradients, these benefits might be offset by the increased computational demands of inference. Scaling PC to deeper models presents a fundamental challenge, requiring further research into more efficient inference algorithms or architectural innovations that leverage PC’s strengths without sacrificing performance. Strategies like hierarchical inference or alternative update schemes may be necessary to unlock PC’s full potential in training very deep networks. Ultimately, resolving the scalability issue is key to realizing PC’s long-term applicability in practical, large-scale deep learning tasks.

More visual insights

#

More on figures

This figure shows that the origin saddle of the loss function is not strict for deep linear networks (DLNs) while it is a strict saddle for the equilibrated energy. The figure shows 3 examples of linear networks with varying depths, from 1 to 3 hidden layers. The plots of the MSE loss L(0) and the equilibrated energy F*(0) around the origin are presented. In the bottom row, the training losses of SGD with initialisation close to the origin are presented for each network. One-dimensional networks allow for a complete visual representation of the landscape, while the 2-D wide network is projected onto the max and min eigenvectors of the Hessian for visualization. It demonstrates that even though the loss landscape has degenerate saddles, the equilibrated energy does not.

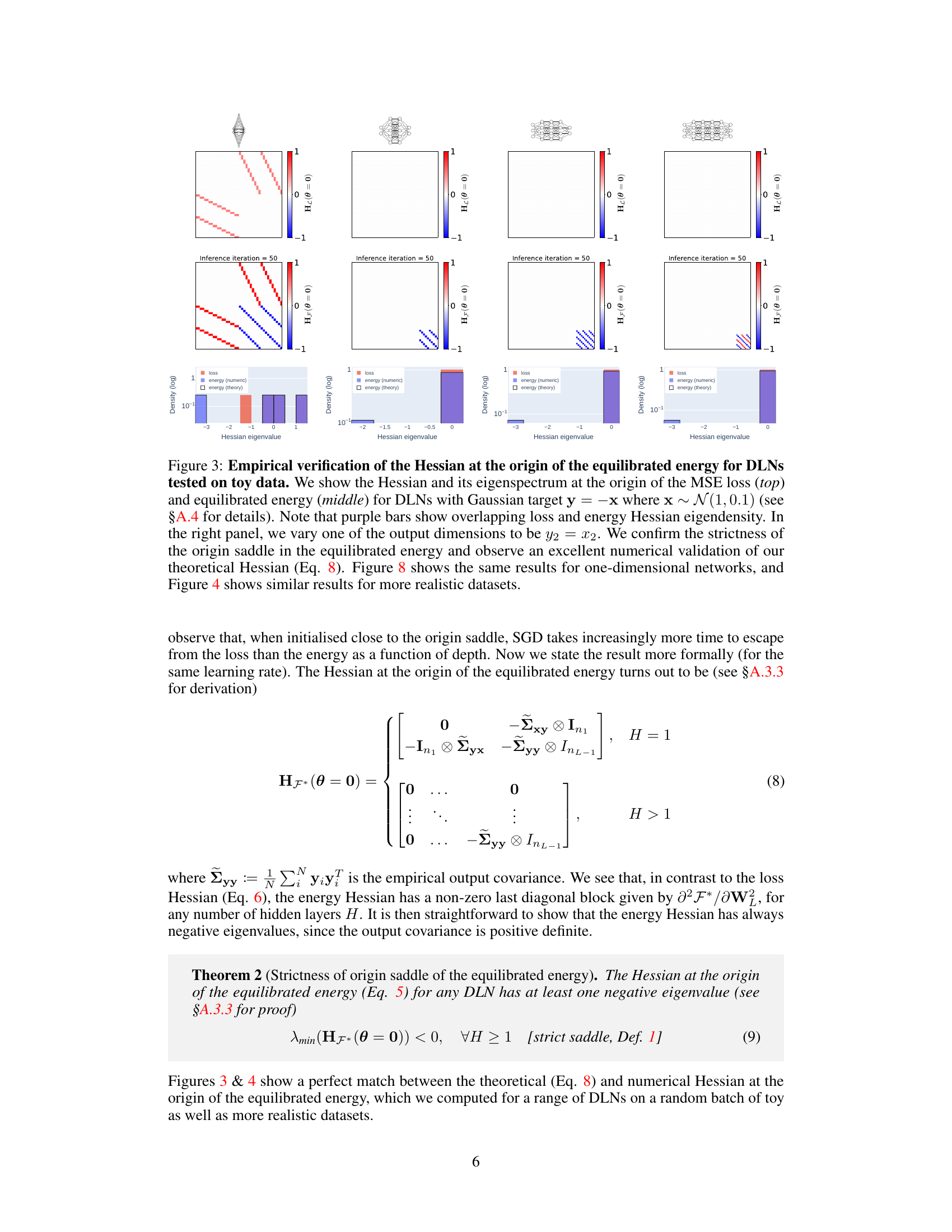
This figure empirically validates the theoretical results about the Hessian at the origin of the equilibrated energy for deep linear networks. It shows a comparison of the Hessian and its eigenspectrum for both the MSE loss and the equilibrated energy, demonstrating a perfect match between theoretical predictions and numerical results. The plots include both 2D heatmaps of the Hessian and histograms of its eigenvalues. A variation on the experiment is also shown, altering the target variable to highlight the robustness of the results.

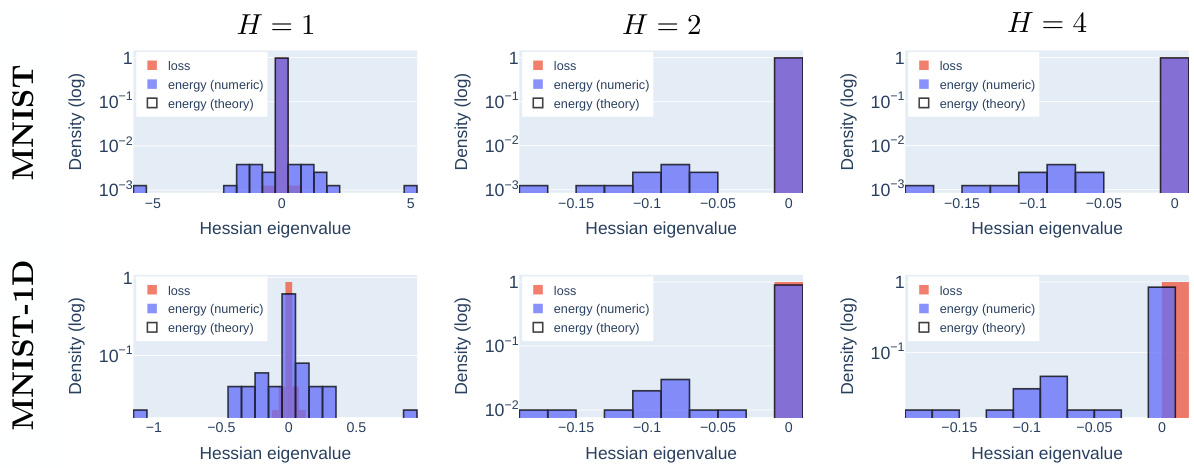
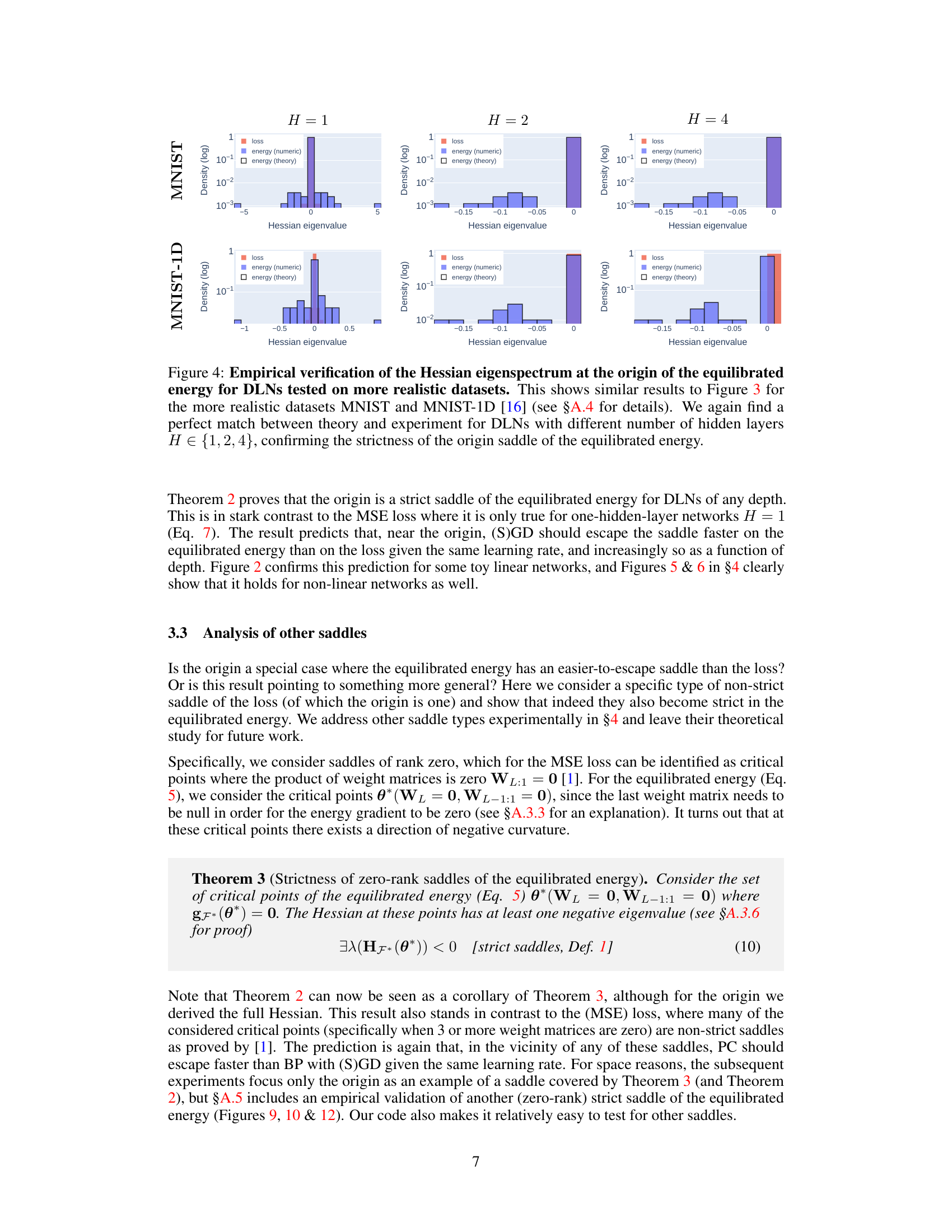
This figure empirically validates the theoretical findings about the Hessian at the origin of the equilibrated energy for deeper linear networks. It compares the numerically computed Hessian eigenspectrum to the theoretical one for MNIST and MNIST-1D datasets and for networks with 1, 2 and 4 hidden layers. The strong agreement supports the theory that the origin saddle of the equilibrated energy is strict, even for realistic datasets.

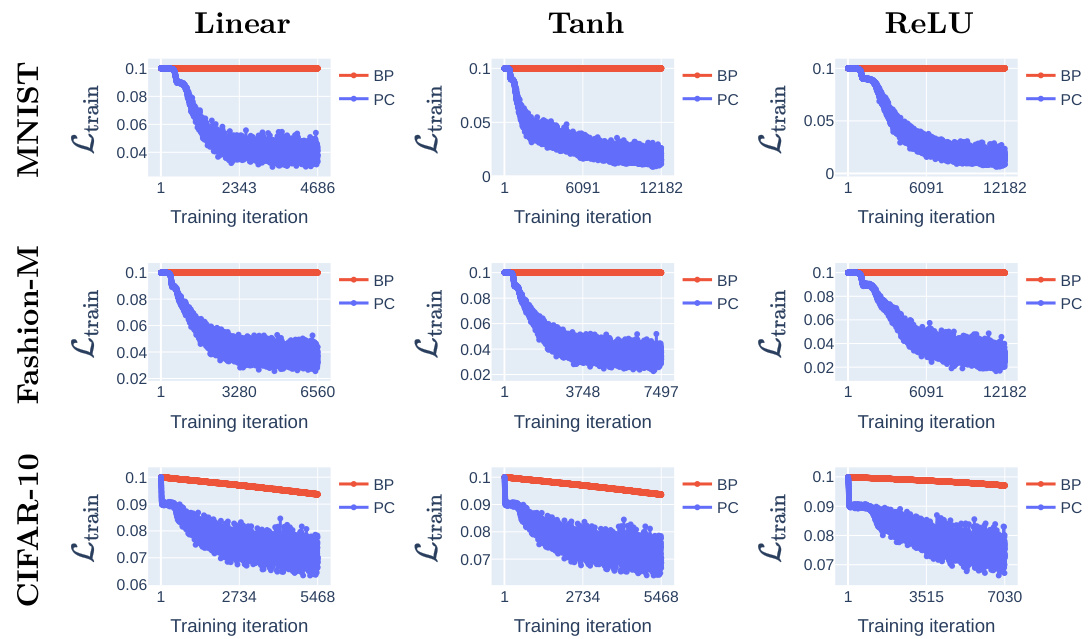
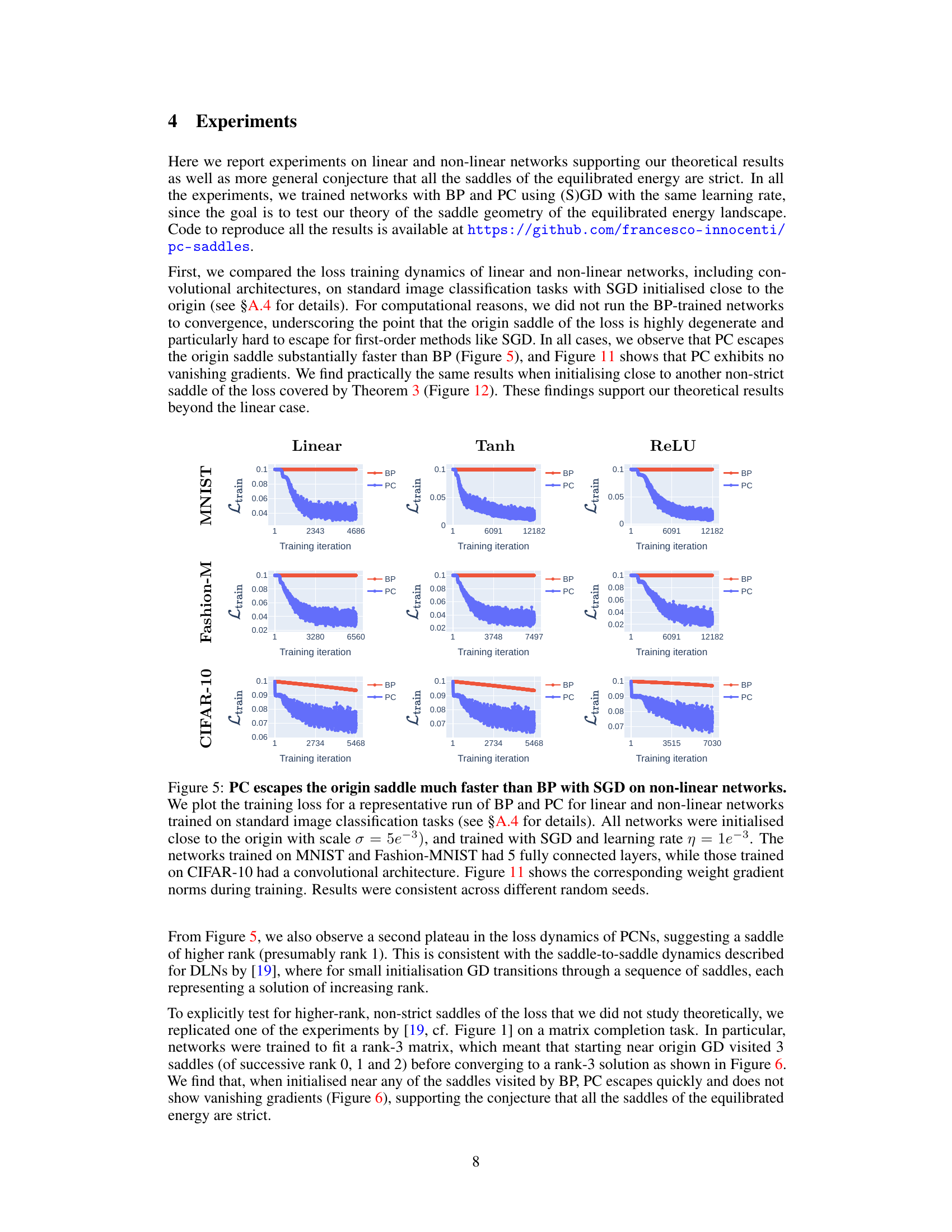
This figure compares the training loss dynamics of backpropagation (BP) and predictive coding (PC) on various network architectures (linear, Tanh, ReLU) and datasets (MNIST, Fashion-MNIST, CIFAR-10). It demonstrates that PC escapes the origin saddle significantly faster than BP. The consistent performance across different datasets and network types supports the claim that PC inference improves the loss landscape’s geometry.

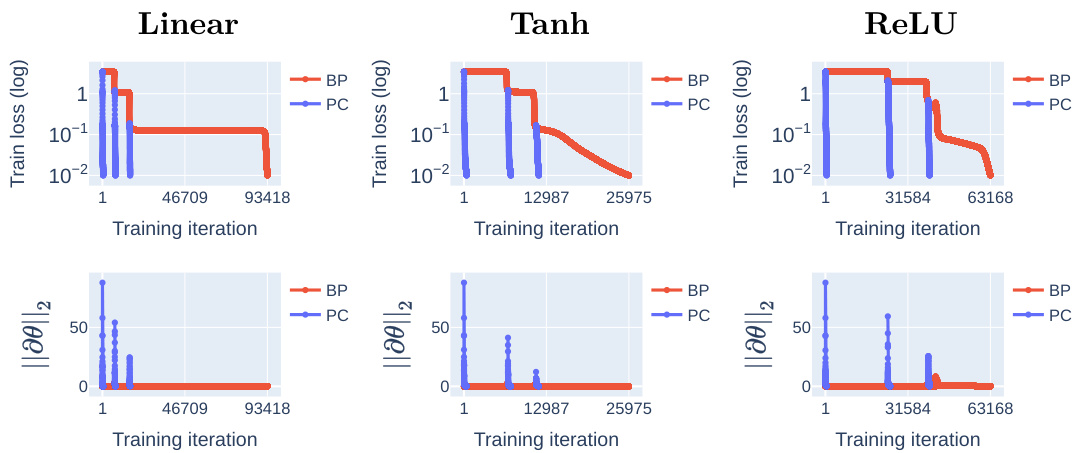
This figure compares the training loss dynamics of linear and non-linear networks (with linear, Tanh, and ReLU activations) trained using BP and PC, respectively, with SGD initialised near the origin. The results show that PC escapes the origin saddle significantly faster than BP for all network types and datasets (MNIST, Fashion-MNIST, and CIFAR-10). The figure also references a supplementary Figure (Figure 11) showing weight gradient norms that support the faster convergence observed with PC.

This figure shows the training and testing loss, along with the gradient norm for linear networks with different architectures. The results are averaged over five runs with different random initializations. The figure highlights the faster convergence of Predictive Coding (PC) compared to Backpropagation (BP), particularly noticeable in the wide network. The plot also demonstrates how PC avoids vanishing gradients.

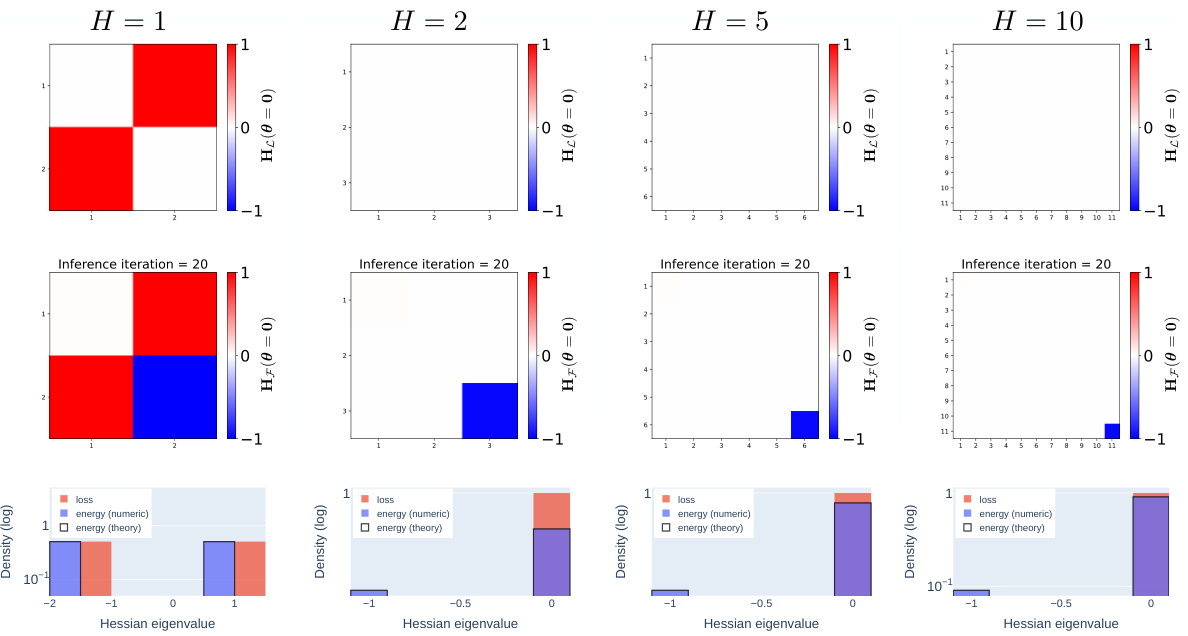
This figure empirically validates the theoretical Hessian at the origin of the equilibrated energy. It compares the Hessian and its eigenspectrum for the MSE loss and the equilibrated energy of deep linear networks (DLNs) on toy Gaussian data. The results confirm the strictness of the origin saddle in the equilibrated energy and demonstrate a high level of agreement between the numerical and theoretical results, further strengthened by showing consistent findings in one-dimensional networks and more realistic datasets.

This figure empirically validates Theorem 3 of the paper, which states that zero-rank saddles of the MSE loss become strict saddles in the equilibrated energy. It shows the Hessian eigenspectra for both the MSE loss and the equilibrated energy at a zero-rank saddle (other than the origin) for deep linear networks (DLNs). The experiment is performed on a simple toy dataset and the results are then compared to results from experiments on the MNIST and MNIST-1D datasets (shown in Figure 10). The results strongly support the theoretical findings.

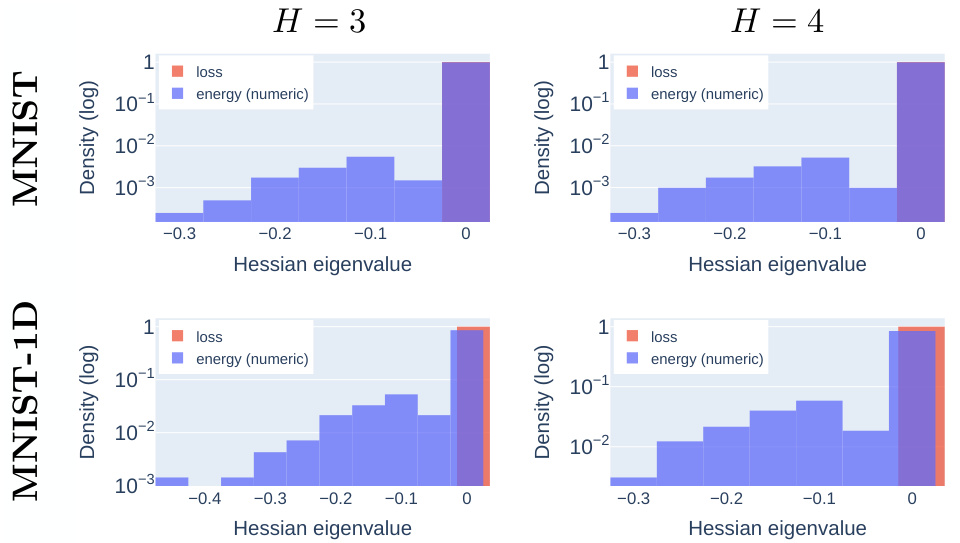
This figure empirically validates the theoretical findings about the strictness of zero-rank saddles in the equilibrated energy landscape. It compares the Hessian eigenspectrum of the MSE loss and the equilibrated energy at a specific zero-rank saddle point (other than the origin) for deep linear networks trained on MNIST and MNIST-1D datasets. The results demonstrate that this zero-rank saddle is strict in the equilibrated energy but not in the MSE loss.

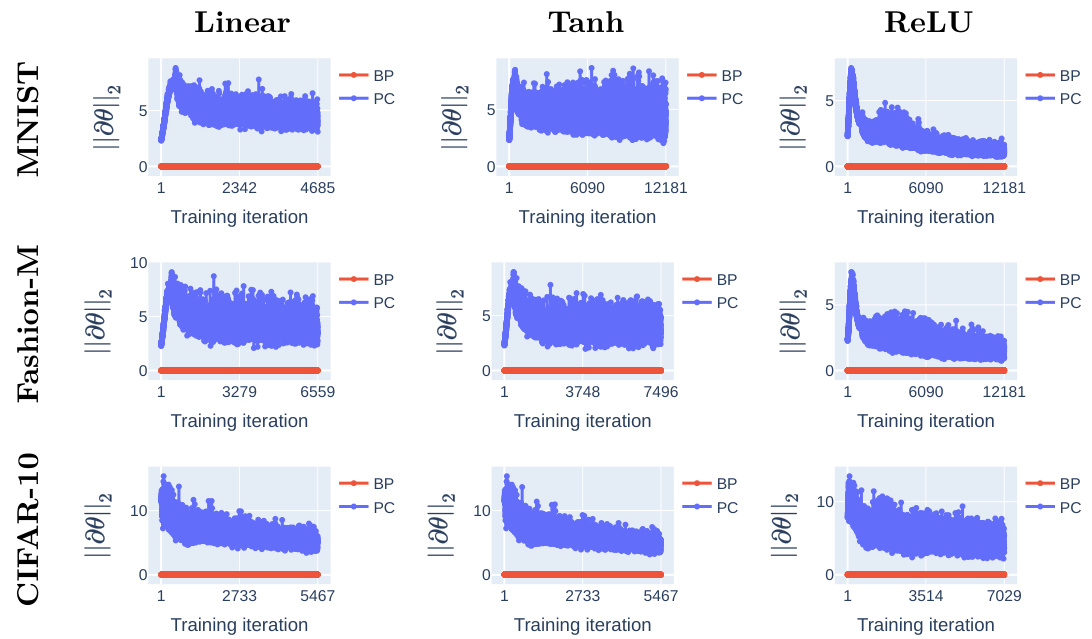
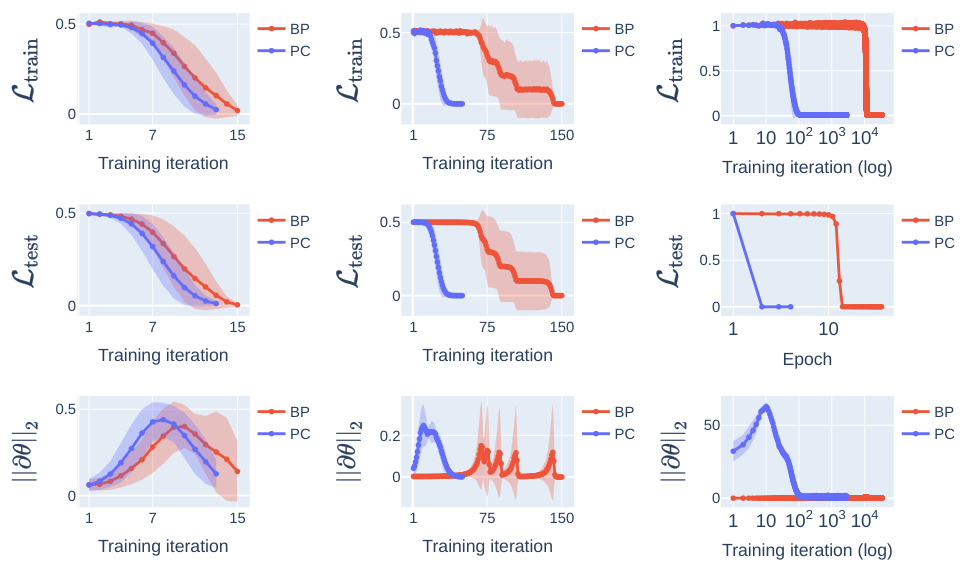
This figure compares the training loss dynamics of linear and non-linear networks trained with backpropagation (BP) and predictive coding (PC) using stochastic gradient descent (SGD). The results demonstrate that PC escapes the origin saddle significantly faster than BP across various network architectures and datasets (MNIST, Fashion-MNIST, CIFAR-10). The figure also shows that the weight gradient norms during training using PC do not exhibit vanishing gradients, unlike BP.

This figure compares the training loss dynamics of linear and non-linear networks trained with BP and PC using SGD. The networks were initialized close to the origin saddle. The results show that PC escapes the origin saddle significantly faster than BP, and no vanishing gradients are observed in PC.

Full paper

#