↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Agent-based models (ABMs) are widely used for simulating complex systems, often relying on origin-destination matrices (ODMs) that capture spatial interactions. However, creating accurate ODMs is computationally expensive, particularly when dealing with high-resolution data or limited observations. Existing methods often resort to approximations, leading to inaccuracies and inefficiency.
This paper introduces GeNSIT, a new framework that addresses these limitations. GeNSIT uses a neural differential equation to learn the intensity of agent trips directly in the discrete ODM space. This makes it significantly faster and more accurate than previous methods, as demonstrated by the authors in large-scale simulations of Cambridge, UK and Washington, DC. The framework efficiently handles partial observations and scales well with the size of the problem.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with agent-based models (ABMs) and spatial interaction models (SIMs). It offers a computationally efficient framework for generating origin-destination matrices, a key component in ABM simulations. The framework directly addresses the challenges of handling partially observed data and high-dimensional discrete spaces, making it highly relevant for complex real-world applications. Furthermore, the work opens doors for future research into more sophisticated constraint-based modeling and efficient inference methods within the context of ABMs and SIMs.
Visual Insights#

This figure illustrates three different approaches for generating origin-destination matrices (ODMs): Agent-based models (ABMs), Spatial Interaction Models (SIMs) using the Harris-Wilson stochastic differential equation (SDE), and the proposed Generative Neural Spatial Interaction Tables (GeNSIT) method. It highlights the computational cost differences between the methods, showing that ABMs are computationally expensive, scaling with O(M log(M)), while GeNSIT scales linearly with O(IJ), where M is much larger than I+J (the number of origin-destination pairs). The figure shows how GeNSIT improves upon SIMs by directly sampling from the discrete space of ODMs conditioned on the continuous approximation from the SIM, thereby avoiding discretization errors.

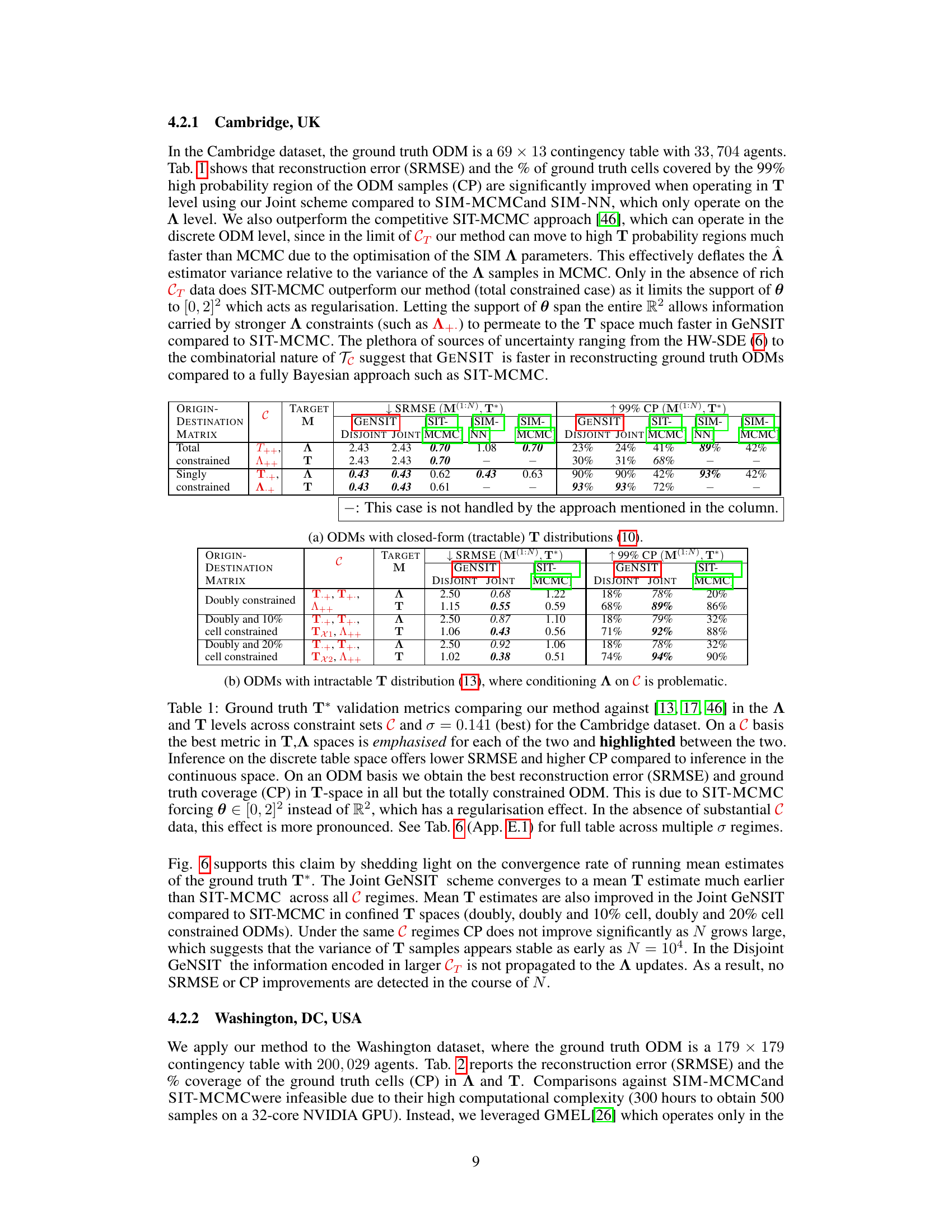
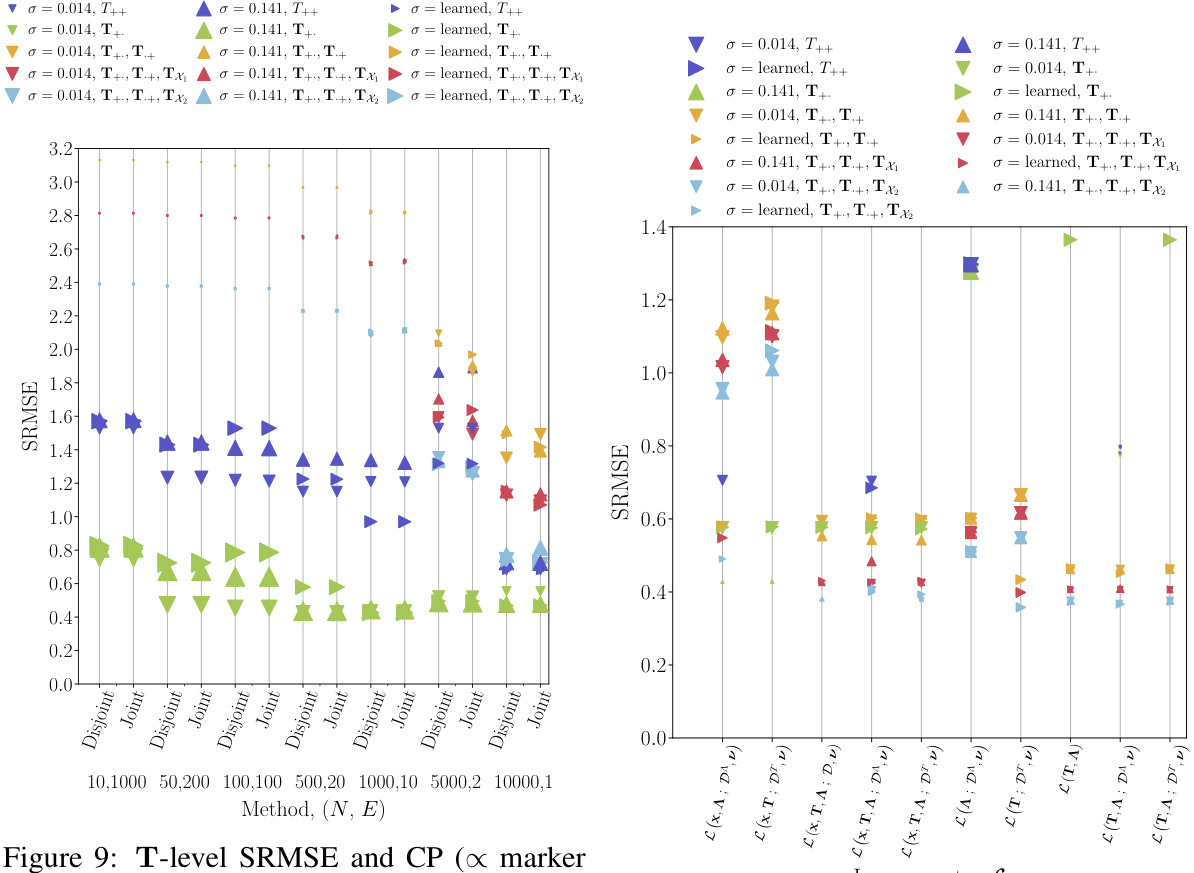
This table compares the performance of the proposed GENSIT method against three other methods (SIM-MCMC, SIM-NN, SIT-MCMC) for reconstructing origin-destination matrices for the Cambridge dataset. It shows the SRMSE (Standardized Root Mean Square Error) and CP (99% high probability region cell coverage probability) for different constraint scenarios (Total, Singly, Doubly, Doubly and 10% cell constrained, Doubly and 20% cell constrained) and two levels (A and T) with best σ values.
In-depth insights#
Neural ODEs for ODMs#
The heading ‘Neural ODEs for ODMs’ suggests a novel approach to modeling origin-destination matrices (ODMs) using neural ordinary differential equations (Neural ODEs). This approach likely leverages the continuous-time nature of Neural ODEs to model the dynamic evolution of ODMs over time, capturing complex spatial interactions and temporal dependencies more effectively than traditional discrete-time methods. A key advantage would be the ability to handle incomplete or noisy data, inherent in many real-world ODMs. The continuous representation offered by Neural ODEs provides a natural framework for integrating diverse data sources like traffic counts, mobility patterns, and geographic information, which could lead to more accurate and robust ODM predictions. The use of neural networks within the ODE framework also allows for learning complex non-linear relationships between variables, potentially improving model flexibility and predictive power. However, challenges remain. Training and inference with Neural ODEs can be computationally expensive, requiring careful consideration of model complexity and optimization strategies. Furthermore, interpreting the learned parameters and understanding the model’s behavior could be complex, necessitating further investigation into explainability techniques. Overall, the proposal of Neural ODEs for ODMs is promising for developing more sophisticated and accurate models for various applications requiring spatial interaction analysis.
GENSIT Framework#
The GENSIT framework offers a novel approach to generating origin-destination matrices (ODMs) within agent-based models (ABMs). It directly addresses the limitations of existing methods by operating on the discrete ODM space, avoiding continuous approximations and their associated errors. Key to GENSIT is its neural calibration of Spatial Interaction Models (SIMs), leveraging neural networks to efficiently learn the underlying spatial interactions. This linear scaling with the number of origin-destination pairs drastically improves computational efficiency. Furthermore, GENSIT allows for flexible incorporation of various summary statistics constraints, enhancing its ability to handle partially observed data. The framework’s ability to efficiently sample from complex discrete distributions of ODMs using closed-form sampling or Gibbs Markov Basis sampling, depending on constraint complexity, is another significant contribution. Overall, GENSIT provides a powerful, efficient, and flexible tool for generating high-resolution, realistic ODMs in ABMs, improving accuracy, scalability, and handling of partially observed data.
Scalable ABM Inference#
Scalable ABM inference presents a significant challenge in the field of agent-based modeling. Traditional methods often struggle to handle the computational complexity of large-scale ABMs, limiting their applicability to real-world scenarios. A key focus is developing efficient algorithms and computational techniques that reduce the computational cost while maintaining accuracy. This could involve leveraging advanced statistical methods, parallel computing, or machine learning approaches. Improved scalability allows for more realistic simulations with a greater number of agents and more detailed agent interactions. Moreover, scalable inference enables more thorough exploration of the parameter space and facilitates better model calibration and validation. The development of new inference methodologies designed specifically for ABMs would significantly contribute to the field, including Bayesian methods that incorporate uncertainty, or approaches that focus on learning from partial or aggregated data. Addressing scalability issues in ABM inference is crucial for expanding the applications of ABMs to diverse problems requiring high-resolution and large-scale modeling.
Real-world Case Studies#
The evaluation of the proposed framework on real-world datasets is crucial for demonstrating its practical applicability. The selection of diverse locations, such as Cambridge, UK and Washington, D.C., USA, allows for a comprehensive assessment of the model’s performance across different urban contexts and data characteristics. Analyzing the results from these case studies provides insights into the model’s strengths and weaknesses when applied to realistic, complex scenarios. A detailed comparison with existing methods is also essential, highlighting the advantages and limitations of the proposed framework in comparison. The presence of ground truth data is vital for a robust assessment of accuracy, allowing for the calculation of appropriate metrics to quantify the performance. Furthermore, a thorough discussion of the challenges and limitations encountered during the implementation of the real-world studies is crucial for providing a balanced evaluation and highlighting areas for future improvements.
Future Research#
Future research directions stemming from this work could explore several promising avenues. Extending GeNSIT to handle more complex, higher-order constraints on the ODM would enhance its applicability to real-world scenarios with intricate spatial dependencies. Investigating alternative neural network architectures beyond the current multi-layer perceptron could lead to improved efficiency and performance. Furthermore, developing more sophisticated methods for handling uncertainty in the agent trip intensities (A) and integrating them into the framework would yield a more robust approach. Finally, applying GeNSIT to other domains, such as ecological inference or neuroscience where similar discrete contingency table estimation problems exist, would showcase the model’s broader utility and potential.
More visual insights#
More on figures
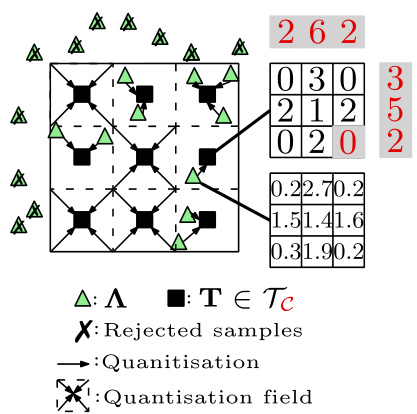
This figure illustrates the challenges of sampling discrete origin-destination matrices directly from the constrained space Tc. The figure shows a 3x3 contingency table (ODM) with summary statistics (C_T) represented as constraints. The space of possible tables satisfying the constraints is shown, and it is demonstrated that directly sampling from this constrained space is difficult, leading to either high rejection rates (many samples are rejected because they don’t meet the constraints) or poor exploration of the distribution (samples don’t sufficiently cover the entire space of valid tables). The problem is further complicated by continuous approximations of the ODM using Spatial Interaction Models (SIMs), which require subsequent quantization, potentially introducing further errors.
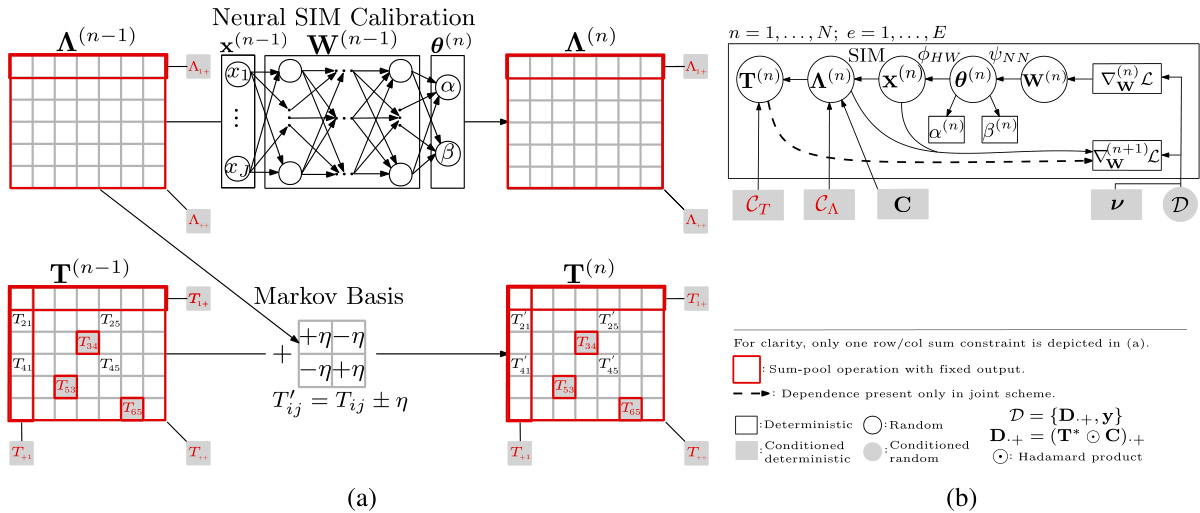
This figure illustrates the GENSIT framework. Panel (a) shows the iterative process of the algorithm, moving between neural SIM calibration (intensity A) and Markov basis sampling (discrete ODM T). Panel (b) provides a plate diagram clarifying the model’s structure and the flow of information, highlighting the ‘joint’ and ‘disjoint’ sampling schemes. The joint scheme incorporates feedback from T into the loss function, whereas the disjoint scheme does not. The figure also shows the complexities associated with intensity and table sampling.

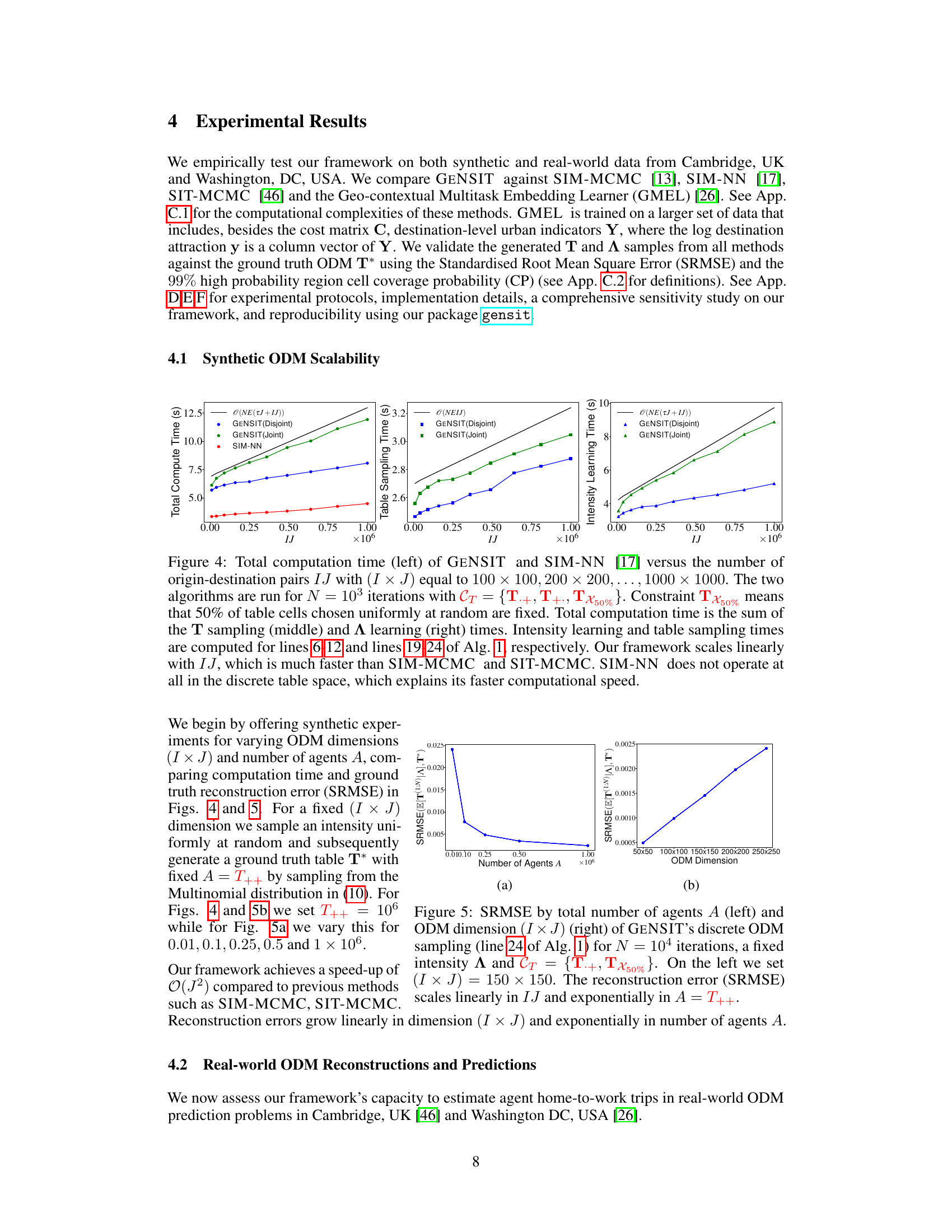
This figure compares the computation time of GENSIT and SIM-NN for varying numbers of origin-destination pairs. It shows that GENSIT’s computation time scales linearly with the number of origin-destination pairs, while SIM-NN’s time remains relatively constant. The figure also breaks down the computation time into table sampling and intensity learning components.
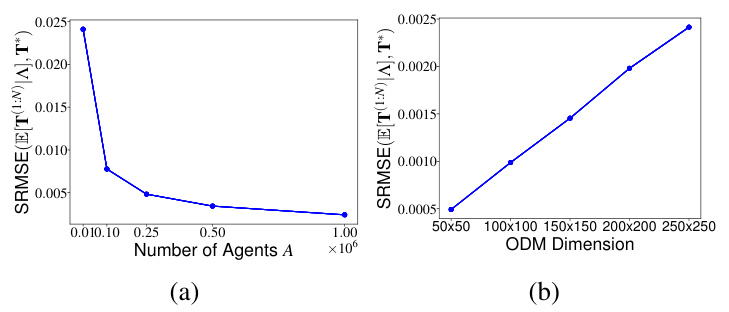
This figure shows the results of an experiment evaluating the scalability and accuracy of the GENSIT method for reconstructing origin-destination matrices (ODMs). The left panel shows that the SRMSE (a measure of reconstruction error) scales exponentially with the total number of agents (A) in the system, while the right panel demonstrates that the SRMSE scales linearly with the dimension (I x J) of the ODM. These results highlight that, while GENSIT scales linearly in the number of origin-destination pairs, the error increases rapidly with the number of agents.

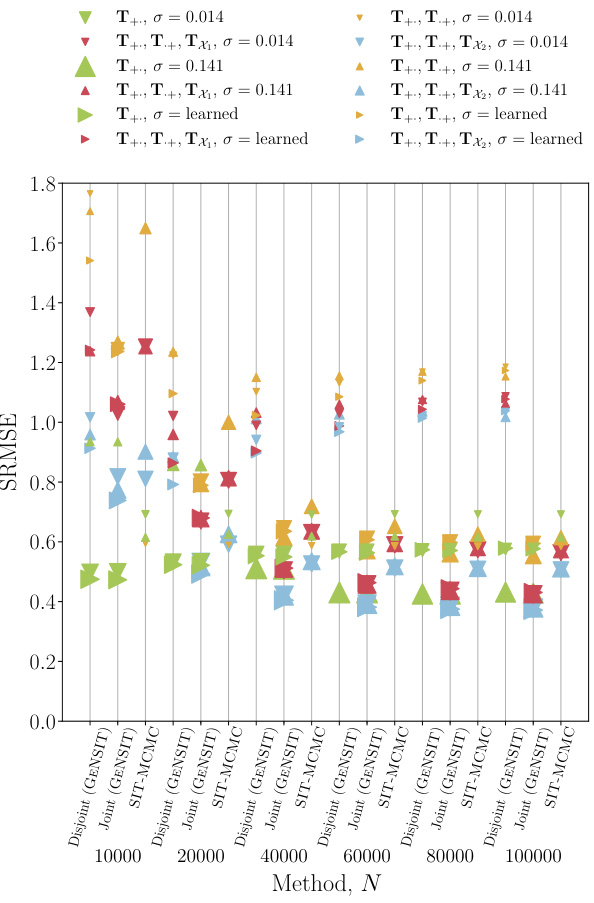
This figure compares the performance of the proposed GENSIT (Joint) algorithm against SIT-MCMC in terms of SRMSE and CP for different constraint sets. The results indicate that GENSIT (Joint) achieves lower SRMSE and higher CP than SIT-MCMC, particularly when considering more complex constraint sets, demonstrating its effectiveness in estimating origin-destination matrices.
This figure illustrates the GENSIT framework, showing the iterative process of neural SIM calibration and discrete ODM sampling. Panel (a) depicts the iterative steps for a single ensemble member, while panel (b) provides a plate diagram representing the process across all ensemble members and iterations. Two sampling schemes are compared: Joint and Disjoint, differing in how table T information is used in the loss function calculation. The framework combines continuous optimization in the intensity (A) space with discrete sampling in the discrete origin-destination matrix (T) space, leveraging the Harris-Wilson SDE to model the continuous intensity. This approach enables efficient generation of constrained discrete ODMs, unlike previous methods that only operate at the continuous level.
This figure illustrates the GENSIT framework, showing its iterative process. Panel (a) depicts a single ensemble member’s iterations through Algorithm 1. Panel (b) provides a plate diagram illustrating the entire ensemble and the relationships between the different components. The framework involves both a continuous (intensity A) and a discrete (ODM T) space. The key difference between the Joint and Disjoint schemes is the information flow; the Joint scheme incorporates the discrete table T into the loss function, whereas the Disjoint scheme does not. Both schemes involve neural calibration of the underlying spatial interaction model (SIM) parameters using the Harris-Wilson SDE.
This figure illustrates the proposed Generative Neural Spatial Interaction Tables (GENSIT) framework. Panel (a) shows the iterative process of the algorithm, highlighting the steps involved in neural SIM calibration, Markov basis sampling, and the overall flow. Panel (b) provides a plate diagram, visualizing the structure and dependencies between different variables in a single iteration and across ensemble members. The figure emphasizes the framework’s ability to operate in both continuous (intensity A) and discrete (table T) spaces, contrasting it with existing approaches that only work in the continuous domain. The two schemes, Joint and Disjoint, are distinguished based on whether the table T information is passed to the loss function or not.
More on tables

This table compares the performance of the proposed GeNSIT method against three other methods (SIM-MCMC, SIM-NN, SIT-MCMC) for reconstructing origin-destination matrices (ODMs) using data from Cambridge, UK. It shows the Standardized Root Mean Square Error (SRMSE) and 99% coverage probability (CP) for different constraint scenarios and noise levels (σ). The results highlight GeNSIT’s superior performance, especially when operating directly on the discrete ODM space.
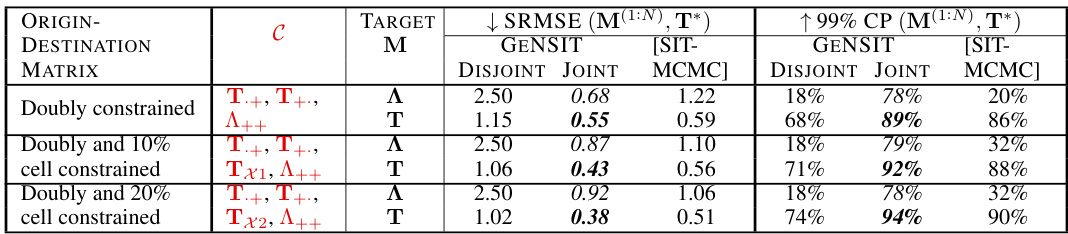
This table presents the results of a comparative study evaluating the performance of the proposed GeNSIT method against existing methods (SIM-MCMC, SIM-NN, SIT-MCMC) for reconstructing origin-destination matrices (ODMs). The comparison is based on two key metrics: Standardised Root Mean Square Error (SRMSE) and 99% High Probability Region cell coverage probability (CP). The results are presented for different constraint settings (C) and noise levels (σ), showcasing the superior performance of GeNSIT, especially in the discrete ODM space, under various scenarios. The table also includes analysis and explanations regarding the impact of constraints and noise on different models.
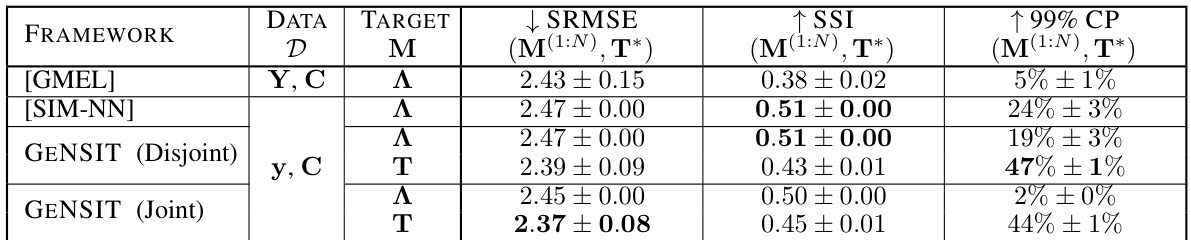
This table presents a comparison of the proposed GENSIT method against three other methods (SIM-MCMC, SIM-NN, SIT-MCMC) for the task of reconstructing origin-destination matrices (ODMs) from real-world data from Cambridge, UK. The comparison is done across different constraint sets and noise levels, and the performance is evaluated using SRMSE and CP metrics. The results show that GENSIT generally outperforms the other methods in terms of reconstruction accuracy, especially when operating directly in the discrete ODM space rather than relying on a continuous approximation.

This table compares the performance of the proposed GENSIT method against three other methods (SIM-MCMC, SIM-NN, SIT-MCMC) in reconstructing and predicting origin-destination matrices (ODMs) for the Cambridge dataset. The comparison is done across different levels of constraint (total, singly, doubly constrained) and different levels of noise (σ). The results show that GENSIT generally performs better in terms of SRMSE (Standardized Root Mean Square Error) and CP (Coverage Probability) when operating directly on the discrete ODM space (T), particularly when sufficient constraints are available. The better performance highlights the advantages of handling the discrete nature of the ODMs directly instead of using continuous approximations.
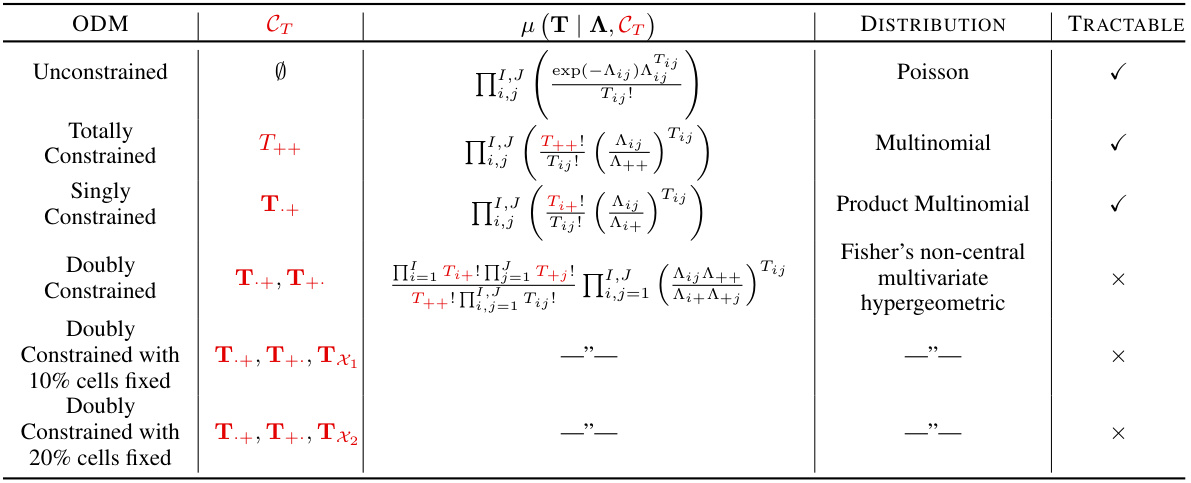
This table lists different target distributions for the origin-destination matrix T, given the continuous agent trip intensity Λ and different sets of constraints CT. The constraints CT specify which summary statistics of T are fixed. For example, ‘Totally Constrained’ means the total number of trips T++ is fixed. Each row shows the distribution that arises in this case and indicates whether sampling from this distribution is tractable (computationally feasible). The table is crucial for understanding the different sampling strategies used in the paper depending on the available data.
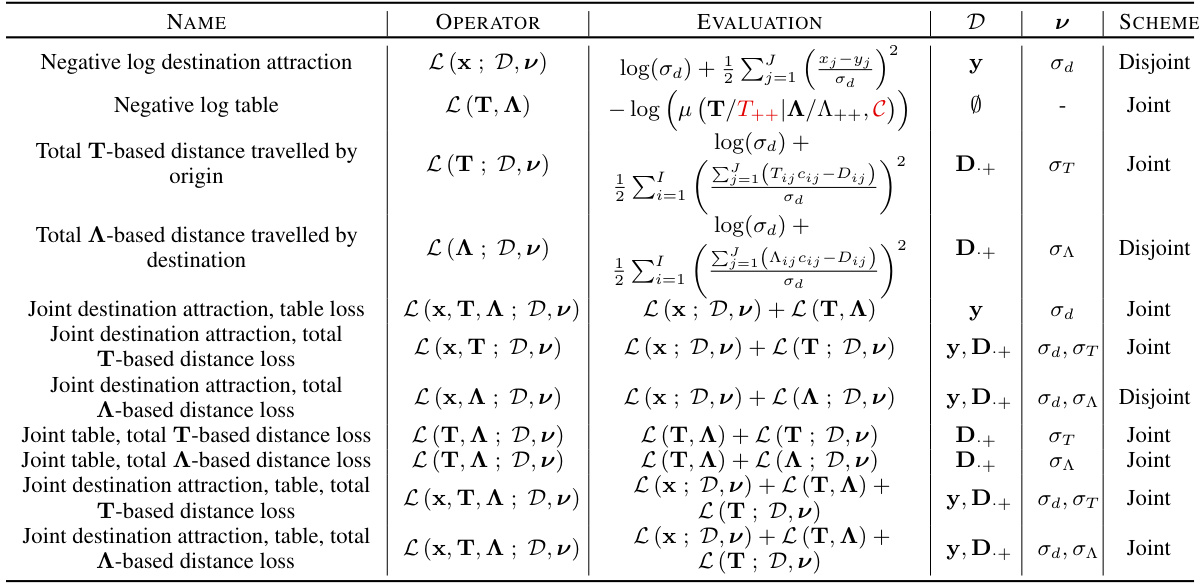
This table presents the results of a comparative study evaluating the performance of the proposed GENSIT framework against existing methods (SIM-MCMC, SIM-NN, SIT-MCMC) on the Cambridge dataset. The comparison is done using the SRMSE and CP metrics for various constraint settings (C) and noise levels (σ). The results demonstrate that GENSIT achieves better reconstruction error and coverage in the discrete table space (T) compared to inference in the continuous intensity space (A).
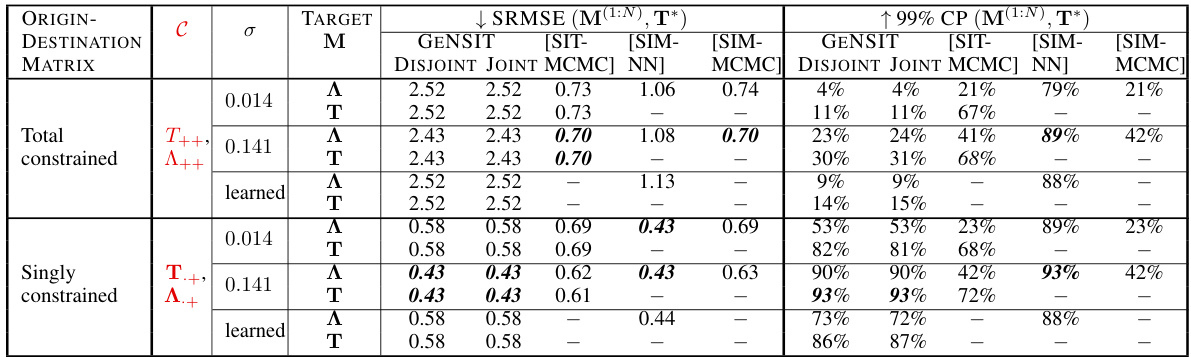
This table compares the performance of the proposed GeNSIT method against three other methods (SIM-MCMC, SIM-NN, SIT-MCMC) for reconstructing origin-destination matrices for the Cambridge dataset. It shows the SRMSE (Standardized Root Mean Square Error) and CP (99% High Probability Region cell coverage probability) for different constraint levels (total, singly constrained, and doubly constrained) and noise levels (σ). The results demonstrate that GeNSIT generally achieves lower SRMSE and higher CP, particularly when operating directly on the discrete ODM (T) space rather than the continuous intensity (A) space. The performance differences are more pronounced when rich summary statistic data (C) is available.

This table compares the performance of the proposed GeNSIT method against three other methods (SIM-MCMC, SIM-NN, SIT-MCMC) on the Cambridge dataset. It shows the SRMSE (Standardized Root Mean Square Error) and CP (99% high probability region cell coverage probability) for different constraint levels (totally constrained, singly constrained, doubly constrained, doubly constrained with 10% and 20% of cells fixed). The results highlight that the GeNSIT method, especially the Joint scheme, outperforms others in terms of accuracy and coverage, particularly when operating on the discrete table level (T).

This table presents a comparison of the proposed GENSIT model against three other models (SIM-MCMC, SIM-NN, and SIT-MCMC) for reconstructing origin-destination matrices (ODMs) for the Cambridge dataset. The comparison is based on several metrics, including the Standardized Root Mean Square Error (SRMSE) and the 99% high probability region cell coverage probability (CP). The table highlights the superior performance of GENSIT in terms of reconstruction accuracy and coverage probability, particularly when operating directly in the discrete ODM space and for scenarios with less constraint data.

This table compares the performance of the proposed GeNSIT method against three other methods (SIM-MCMC, SIM-NN, SIT-MCMC) for reconstructing origin-destination matrices (ODMs) for the Cambridge dataset. The comparison is made across different levels of constraint (total, singly, doubly constrained) and different levels of noise in the data. Key metrics used for comparison include the Standardized Root Mean Square Error (SRMSE) and the 99% High Probability Region cell coverage probability (CP). The results highlight the advantages of GeNSIT, particularly in achieving lower SRMSE and higher CP when operating in the discrete ODM space (T-level) compared to the continuous space (A-level).
Full paper#