↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Variance Exploding (VE) diffusion models have shown superior performance in generating data from low-dimensional manifolds, but their theoretical understanding lags behind. Existing works suffer from slow forward convergence rates, hindering efficient sampling. This limitation stems from the absence of a drift term in the standard VE forward process.
This paper introduces a novel drifted VESDE forward process that incorporates a drift term, enabling a significantly faster forward convergence rate. This allows for the first time, efficient polynomial sample complexity for VE models under the reverse SDE process, while also accommodating unbounded diffusion coefficients. The researchers further propose a unified tangent-based analysis framework to examine both reverse SDE and PFODE processes simultaneously, proving the first quantitative convergence guarantee for state-of-the-art VE models under PFODE. The effectiveness of the drifted VESDE is validated through both synthetic and real-world experiments.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on diffusion models because it addresses the critical issue of slow forward convergence in variance exploding (VE) models. It provides novel theoretical frameworks and a drifted VESDE process to improve the sample complexity, bridging the gap between theory and the high performance of state-of-the-art models. This work significantly advances our understanding of VE-based models and provides a new direction for future research.
Visual Insights#

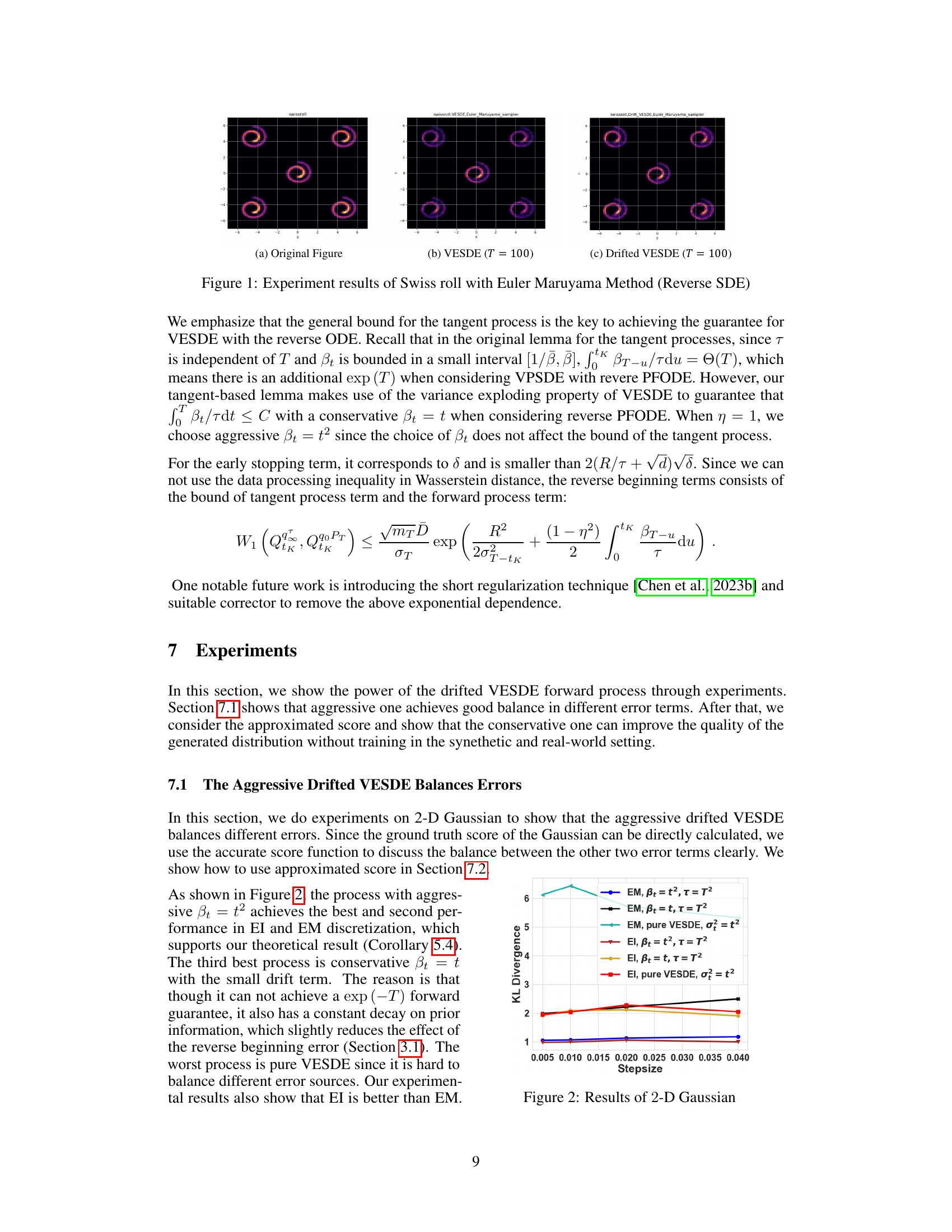
This figure compares the results of sampling from a Swiss roll dataset using three different methods: the original dataset, the Variance Exploding Stochastic Differential Equation (VESDE) sampler, and the Drifted VESDE sampler. The images show that the Drifted VESDE sampler produces samples that more closely resemble the original data distribution, especially in terms of capturing the curvature and density of the manifold.

This table presents the KL divergence results between the generated distribution and the ground truth distribution for different settings. The settings include two different forward processes (pure VESDE and drift VESDE), two different diffusion times (T = 100 and T = 625), two different reverse processes (reverse SDE and reverse PFODE), and two different synthetic datasets (1-D GMM and Swiss roll). The results show that the drift VESDE generally achieves lower KL divergence compared to the pure VESDE, indicating its effectiveness in improving the generated sample quality.
In-depth insights#
Drifted VESDE#
The proposed “Drifted VESDE” method introduces a drift term to the Variance Exploding Stochastic Differential Equation (VESDE) forward diffusion process. This crucial modification addresses a key limitation of standard VESDE, its slow 1/poly(T) forward convergence rate, improving it to exp(-T). The faster convergence significantly reduces the distance between the forward process’s marginal distribution and pure Gaussian noise, a major factor affecting the sample complexity of reverse diffusion processes. The drift term effectively eliminates data information during the forward process, accelerating convergence to Gaussian noise. The authors further demonstrate improved sample complexity for VE-based models under the reverse SDE and PFODE processes through a unified tangent-based analysis framework. Their theoretical findings show that the drifted VESDE balances various error terms, enabling efficient sample generation. Empirical evaluations on synthetic and real-world datasets confirm the superior performance of the drifted VESDE, showcasing its practical relevance. The method’s ability to achieve optimal results without additional training highlights its efficiency and potential for broader applications.
Manifold Hypothesis#
The manifold hypothesis, a cornerstone of modern machine learning, posits that high-dimensional data, like images or text, often lies on a lower-dimensional manifold embedded within the higher-dimensional ambient space. This means that while the data appears spread out in many dimensions, its intrinsic structure is far simpler. This is crucial for diffusion models, as it implies that generating realistic samples doesn’t require navigating the full complexity of the high-dimensional space. Instead, the model can focus on learning the underlying manifold’s structure. The manifold hypothesis justifies the use of variance-exploding SDEs, as these processes are well-suited to exploring and generating samples from low-dimensional manifolds. However, it’s vital to acknowledge that this hypothesis is an assumption, not a proven fact, and its validity varies across datasets. The success of VE-based diffusion models provides strong empirical evidence supporting the manifold hypothesis, at least for some types of data. Future research could focus on developing more rigorous theoretical frameworks and empirical analyses to further probe the manifold hypothesis’s limitations and scope.
Reverse SDE/PFODE#
The core of diffusion models lies in their ability to reverse a forward stochastic process, which gradually adds noise to the data. This reversal is achieved using either a Reverse Stochastic Differential Equation (SDE) or a Probability Flow Ordinary Differential Equation (ODE, PFODE). Reverse SDEs introduce stochasticity into the reversal process, allowing for exploration of the probability landscape and potentially leading to higher-quality samples. This comes at the cost of increased computational expense. In contrast, PFODE offers a deterministic path, resulting in faster sample generation but potentially sacrificing sample diversity. The choice between these methods represents a trade-off between sample quality and computational efficiency. The paper likely investigates this trade-off, potentially proposing novel methods or analyses to improve either the sample quality of PFODE or the computational efficiency of reverse SDEs, or even a hybrid approach that optimally balances both.
Sample Complexity#
The concept of ‘sample complexity’ in the context of variance exploding diffusion models is crucial. It quantifies the number of samples needed to achieve a certain level of accuracy in generating data. The paper highlights that existing theoretical analyses of variance exploding (VE) models suffer from slow forward convergence rates, which is a significant hurdle to achieving good sample complexity. This slow convergence is primarily attributed to the absence of a drift term in the standard VE stochastic differential equation (SDE). The core contribution focuses on introducing a drifted VESDE, which incorporates a drift term, enabling a faster convergence rate. This improved rate is essential for balancing various error terms in the reverse diffusion process, ultimately leading to lower sample complexity. The authors prove this theoretical improvement under realistic assumptions such as the manifold hypothesis. This is a significant advancement, as it bridges the gap between the practical performance and theoretical understanding of VE-based models. The empirical validation using synthetic and real-world datasets further corroborates the superior sample efficiency of the proposed drifted VESDE.
Future Work#
The paper’s ‘Future Work’ section suggests several promising avenues. Extending the theoretical framework to incorporate approximated score functions is crucial for bridging the gap between theory and practice. This would strengthen the analysis’s real-world applicability. Another key area is exploring different settings for the variance exploding SDE, such as examining other choices for the function βt, to potentially uncover more efficient sampling strategies. The authors also plan to investigate more sophisticated discretization schemes, beyond the Euler-Maruyama and exponential integrator methods, to further improve accuracy and efficiency. Finally, extensive experimental validation on a broader range of datasets and comparisons with state-of-the-art diffusion models are needed to fully demonstrate the practical benefits of the proposed drifted VESDE. These future directions would enhance the robustness and impact of the research, providing deeper insights into the convergence behavior of VE-based diffusion models.
More visual insights#
More on figures
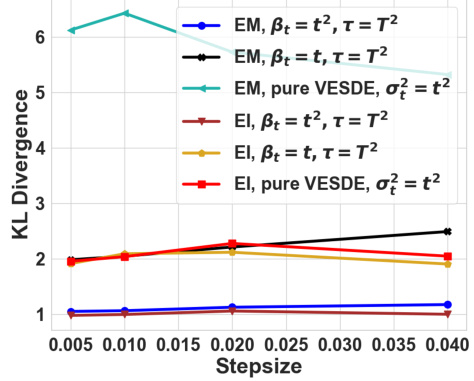
This figure shows the KL divergence results on a 2D Gaussian distribution for different VESDE forward processes and discretization schemes. The processes compared include: aggressive drifted VESDE (βt = t², τ = T²), conservative drifted VESDE (βt = t, τ = T²), and pure VESDE (σt² = t²). Discretization schemes used are Euler-Maruyama (EM) and exponential integrator (EI). The x-axis represents the stepsize, and the y-axis shows the KL divergence. The results demonstrate that the aggressive drifted VESDE achieves the best performance, followed by the conservative drifted VESDE, indicating a superior balance of errors compared to pure VESDE.

This figure shows the qualitative results of CelebA dataset using pure VESDE and drifted VESDE. The top row shows the samples generated by pure VESDE, while the bottom row shows the samples generated by drifted VESDE. The images generated by drifted VESDE have more detail and better visual quality, especially hair and beard details. This is because the conservative drifted VESDE can reduce the influence of dataset information and balance different error terms.

This figure shows the experimental results of the Swiss roll dataset using the Euler Maruyama method with Reverse SDE. It compares the original data distribution (a) with results from a standard Variance Exploding SDE (VESDE) (b) and the new drifted VESDE proposed in the paper (c). The results demonstrate the improvement achieved by the drifted VESDE in capturing the data distribution more accurately than the standard VESDE.
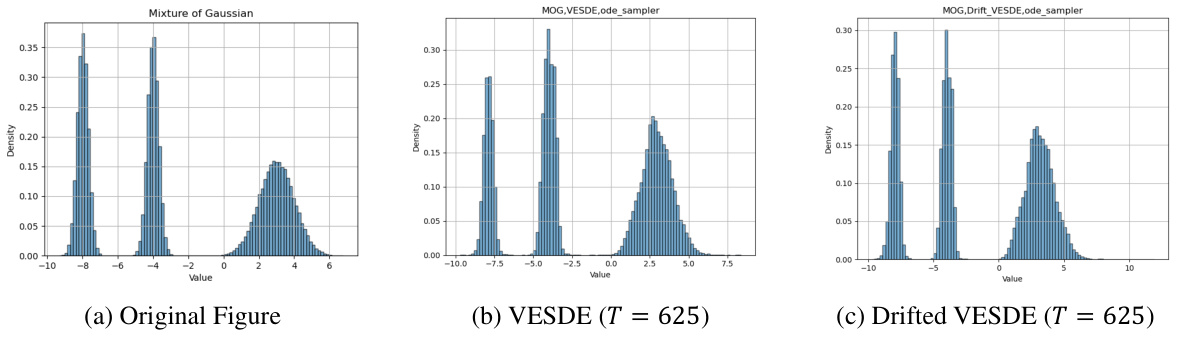
This figure shows the experimental results for a 1D Gaussian Mixture Model (GMM) using reverse probability flow ODE (PFODE). It compares the original GMM distribution (a) to the results obtained using a standard Variance Exploding Stochastic Differential Equation (VESDE) (b), and a modified, drifted VESDE (c). Both VESDE methods used the same T value (625). The plots visually represent the data distribution’s probability density, demonstrating the effect of the drifted VESDE on improving the quality of sample generation by better approximating the target distribution.

This figure shows the results of CelebA dataset experiments comparing the image generation quality of pure VESDE and drifted VESDE models. The images generated by drifted VESDE exhibit more details compared to those generated by pure VESDE, which appear blurry.

The figure shows the comparison of the image generation results between the original VESDE and the proposed drifted VESDE on the CelebA dataset. The images generated by the drifted VESDE show more details (like hair and beard) and appear more realistic compared to those produced by the original VESDE, which appear blurry. This visually demonstrates the improved sample quality achieved by the drifted VESDE without any additional training.
Full paper#