↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
While transformers dominate large language models, recent recurrent models based on linear state-space models (SSMs) show competitive performance. However, a comprehensive understanding of SSMs’ theoretical abilities is lacking. This research addresses this gap by presenting a formal study of SSM capacity compared to that of transformers and traditional RNNs.
The study reveals that SSMs and transformers possess distinct strengths. SSMs effectively solve problems like length-generalizing state tracking and model bounded hierarchical structures optimally, even without stack-like mechanisms. However, the study identifies current SSM designs that limit their expressiveness, like the use of non-negative gates. These limitations are compared to both transformers and RNNs. Results are validated empirically using the Mamba SSM.
Key Takeaways#
Why does it matter?#
This paper is crucial because it bridges the gap in understanding the expressive capabilities of state-space models (SSMs) for language modeling, a rapidly growing area. It provides theoretical foundations and empirical evidence, guiding future SSM-based LLM architectures and improving our understanding of their strengths and limitations compared to transformers and RNNs.
Visual Insights#
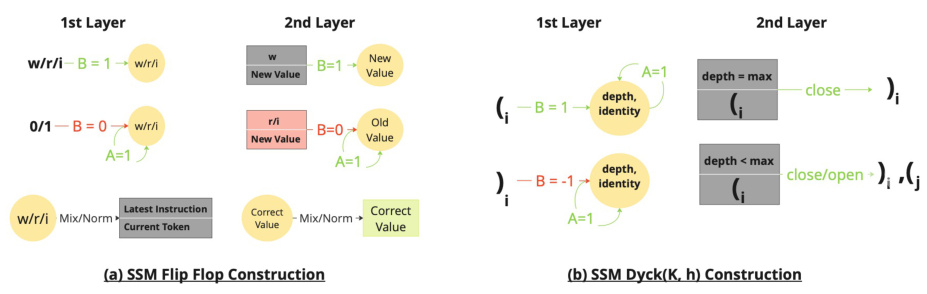
This figure illustrates the SSM constructions for Flip-Flop and Dyck(K, h) languages. Panel (a) shows how a two-layer SSM can model the Flip-Flop language using the first layer to store the instruction and the second to update the state based on whether the instruction is write. Panel (b) shows how a two-layer SSM can model bounded hierarchical structure. The first layer uses a counter to track depth and the second layer uses a flip-flop type of construction to remember the last opening bracket. The overall constructions verify the theorems of the paper.

This table lists seven Tomita grammars, each defined by a regular expression or a description in words. The table also indicates whether each grammar is star-free, a property relevant to the paper’s investigation of the expressive capacity of state-space models.
In-depth insights#
SSM Expressiveness#
The study delves into the expressive capacity of state space models (SSMs) for language modeling, comparing them to transformers and RNNs. A key finding is that SSMs excel in length-generalizing solutions for tasks like flip-flop state tracking, outperforming transformers. However, the analysis reveals design choices, such as non-negative gates in current SSM architectures, that restrict expressiveness, especially hindering their ability to handle tasks like parity checks which transformers also struggle with. The researchers show that SSMs can efficiently model bounded hierarchical structure without explicitly simulating a stack, a capability similar to that of transformers and RNNs. The theoretical findings are substantiated by experiments using a recent state-space model, ‘Mamba’, demonstrating that SSMs are particularly effective for star-free languages but have limitations with counter languages. Overall, the work establishes both the strengths and limitations of SSM expressiveness, providing valuable insights for the design of future language models.
Formal Language Tests#
The heading ‘Formal Language Tests’ suggests an evaluation methodology focusing on the capacity of state-space models (SSMs) to handle formal languages. This approach likely involves presenting the SSMs with various formal language families, such as regular, context-free, and context-sensitive languages. The goal is to assess how well SSMs can learn, generalize, and represent these languages. This would reveal their expressive power, highlighting strengths and limitations when compared to traditional recurrent neural networks (RNNs) and transformers. Key metrics may include accuracy of prediction, length generalization, and resource utilization. Furthermore, the choice of specific formal languages would be crucial: simpler regular languages might reveal basic state-tracking abilities, while more complex languages like context-free or context-sensitive languages would probe capabilities for hierarchical structure representation and longer-range dependencies. The results from these tests would offer significant insights into the computational power of SSMs, ultimately guiding the design and improvement of future language models.
Mamba SSM Results#
The Mamba SSM results section would likely detail the empirical performance of the Mamba state-space model on various language modeling tasks. Key aspects would be the model’s ability to learn and generalize across different formal language classes, including star-free, non-star-free, and counter languages. The results might demonstrate Mamba’s superior performance on star-free languages in comparison to traditional transformers, aligning with the theoretical findings. Conversely, it might show that Mamba struggles with non-star-free languages such as parity. The results might also present a quantitative comparison of Mamba against existing transformer and RNN models on various metrics, such as accuracy, perplexity, and length generalization. Importantly, an analysis of performance across different input lengths would be crucial to gauge the model’s scalability and ability to handle long sequences. The empirical findings would ideally complement and support the theoretical claims regarding the expressive capacity of SSMs, offering valuable insights into their potential advantages and limitations for language modeling.
Bounded Hierarchy#
The concept of “Bounded Hierarchy” in the context of language modeling signifies the capacity of a model to handle hierarchical structures within a defined limit. Unlike unbounded hierarchical structures that allow for infinite nesting of phrases or clauses, bounded hierarchies impose a constraint on the depth of nesting. This limitation is crucial because human language, while exhibiting hierarchical properties, does not exhibit infinite nesting. The research likely investigates how different model architectures, like state-space models (SSMs) and transformers, handle bounded hierarchies. SSMs may exhibit advantages in modeling bounded hierarchical structures due to their ability to efficiently track states and handle iterative updates, potentially outperforming transformers in these specific tasks. This section likely presents theoretical analyses and experimental results comparing the performance of these models on tasks involving bounded hierarchies, showing their relative strengths and limitations with respect to memory and computational efficiency. The findings would offer insights into architectural design choices for language models and potentially inspire the development of hybrid models that combine the strengths of both SSMs and transformers.
Future Research#
Future research directions stemming from this paper on state space models (SSMs) for language modeling are multifaceted. Investigating the interplay between SSMs and attention mechanisms is crucial, potentially leading to hybrid architectures that combine the strengths of both. Exploring alternative parameterizations for SSMs that avoid the limitations imposed by non-negativity constraints is key to unlocking greater expressive power. The theoretical findings on the expressive capacity of SSMs, particularly concerning star-free languages and bounded hierarchical structures, suggest avenues for developing more efficient and robust SSM-based language models. Further empirical validation is needed to confirm these findings across different SSM implementations and tasks. Finally, a comprehensive study of the effect of finite precision on SSM performance would be highly valuable. Addressing these research questions will significantly advance the field of SSMs in language modeling.
More visual insights#
More on figures
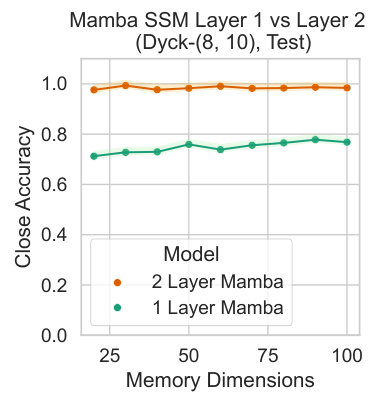
This figure shows the results of an experiment evaluating the performance of the Mamba model on the Dyck(K, h) language. The x-axis represents the number of memory dimensions used in the model, while the y-axis represents the close accuracy achieved. Two lines are plotted, one for a 2-layer Mamba model and another for a 1-layer model. The results demonstrate that the 2-layer model significantly outperforms the 1-layer model across all memory dimensions, thus confirming that a 2-layer architecture is necessary for effectively modeling the bounded hierarchical structure present in the Dyck language.

The figure presents a comparison of Mamba and Transformer models’ performance across various formal languages. The x-axis categorizes languages by type (star-free, non-star-free, counter). The y-axis shows accuracy. The different colored bars within each language category represent results for Mamba and Transformers, broken down by in-distribution and out-of-distribution input lengths. The results align with the paper’s theoretical findings, demonstrating Mamba’s strength on star-free languages and its relative weakness on non-star-free ones, while also showing its ability to model counter languages, albeit with less success in length generalization compared to Transformers.
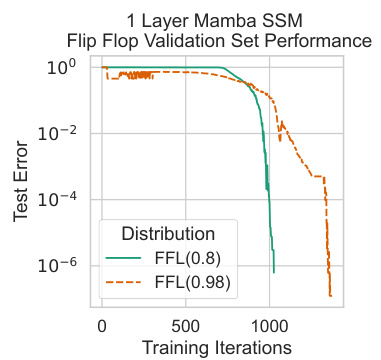
This figure shows the test error on the validation set for the Flip Flop language (LFF) obtained from the training of a one-layer Mamba SSM. The test error is plotted against the number of training iterations. Two different data distributions are shown: FFL(0.8) and FFL(0.98), representing different levels of sparsity in the data. The results demonstrate that Mamba achieves near-zero test error in both distributions, showcasing its ability to generalize well and avoid the failures observed in transformers for this task, as reported by Liu et al. [2023a].

This figure illustrates the state space model (SSM) equations and how SSMs handle the PARITY problem and unbounded counting. Panel (a) shows the core SSM update equations, highlighting the roles of the hidden state (H), input (X), transformation function (φ), and matrices A and B. Panel (b) demonstrates an intuitive approach to recognizing PARITY, which, however, violates constraints, illustrating a key limitation of SSMs in handling parity at arbitrary lengths. Panel (c) shows how SSMs simulate a counter using matrix A and B, successfully modeling the ‘a^nb^n’ language.
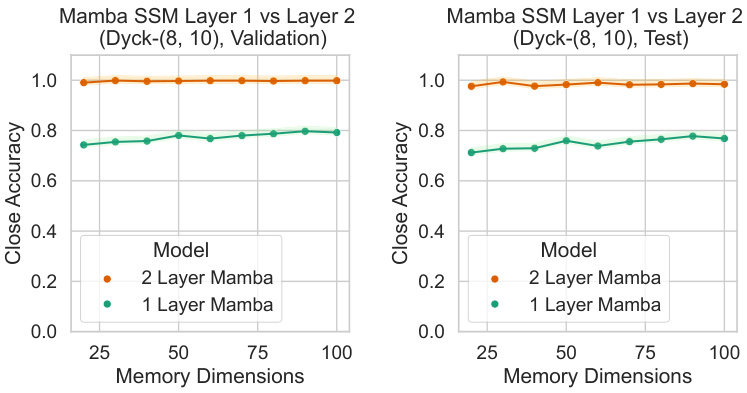
This figure shows the accuracy of Mamba models with varying memory dimensions on the Dyck(8,10) language. The results are presented separately for the development set (lengths < 700) and test set (lengths 700-1400). The test set results are also shown in Figure 4. The plot compares the performance of 1-layer and 2-layer Mamba models, illustrating the impact of model depth and memory capacity on accuracy in predicting this hierarchical language.
More on tables
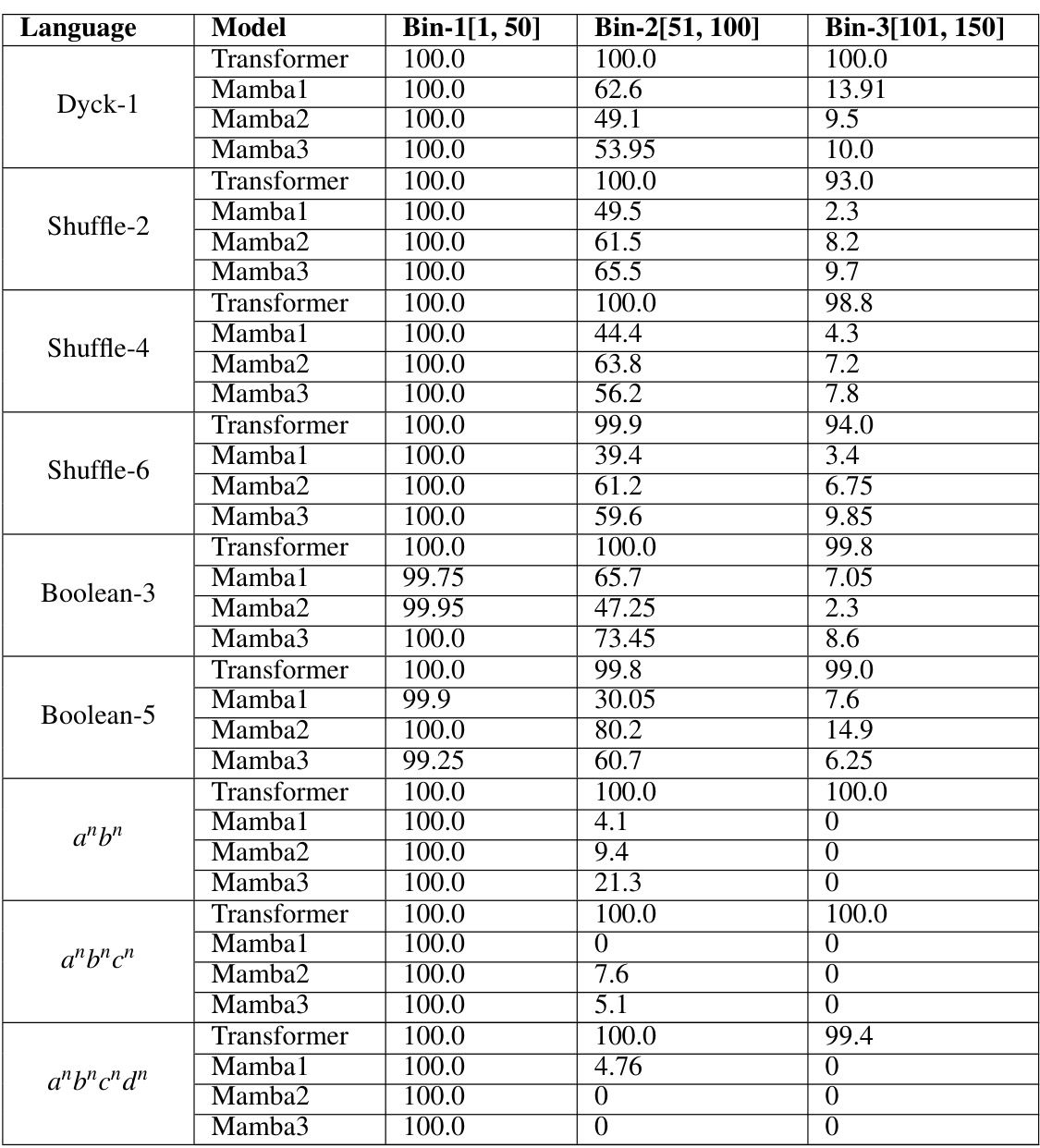
This table compares the performance of Mamba and Transformer models on various counter languages, specifically focusing on the accuracy of these models. It demonstrates Mamba’s performance at different layer counts (1,2,3) and shows results on three input length ranges: [1,50], [51,100], and [101,150]. It also includes a reference to Figure 5 for additional context.

This table compares the performance of Mamba and Transformer models on various regular languages. It shows accuracy on two input length bins ([1,50] and [51,100]). Mamba’s results are reported for different numbers of layers (1,2,3), indicating the best performing layer configuration for each language. Results are also visually represented in Figure 5.
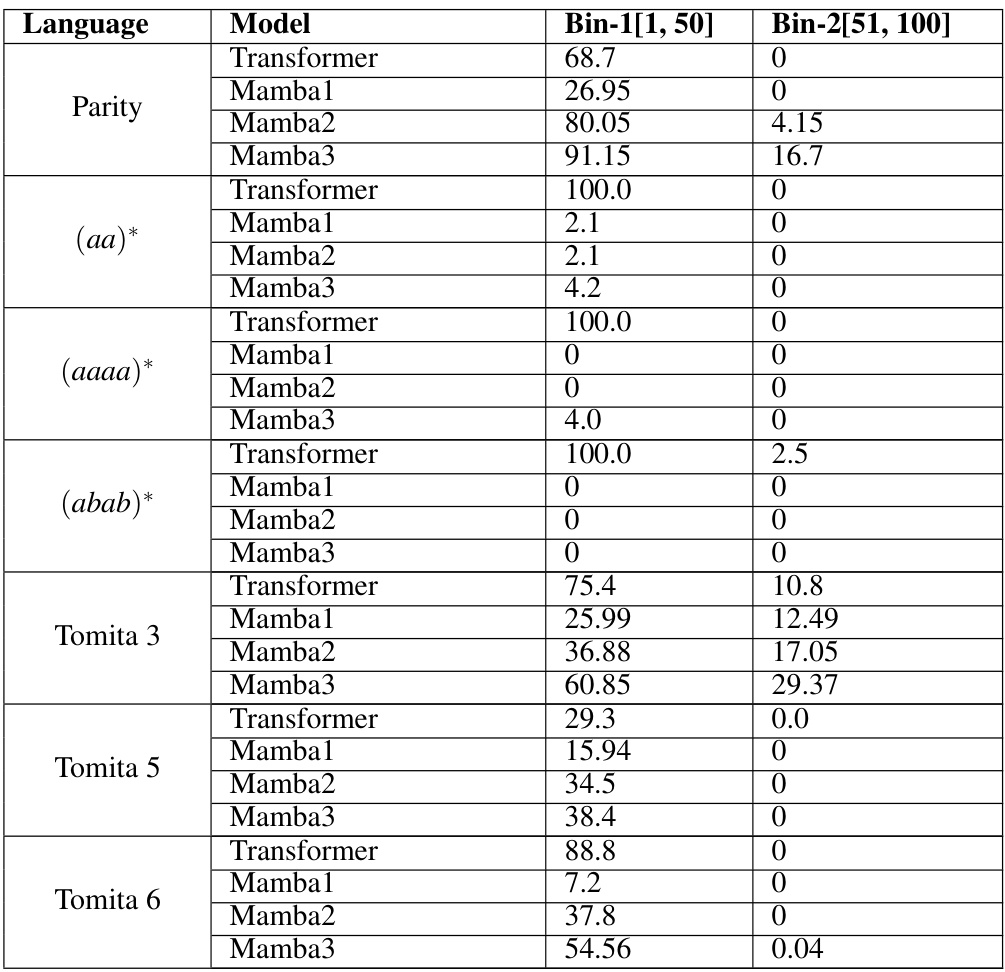
This table presents the accuracy results of Mamba and Transformer models on a subset of regular languages from the Bhattamishra et al. (2020) test suite. It shows the accuracy for three different length bins ([1,50], [51,100], [101,150]). The best-performing layer count (1,2, or 3 layers) for Mamba is reported, and the results are also visually represented in Figure 5 of the paper.
Full paper#



















